2. 中国科学院地理科学与资源研究所, 北京 100101;
3. 中国农业科学院农业资源与农业区划研究所, 北京 100081
2. Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China;
3. Institute of Agricultural Resources and Regional Planning, Chinese Academy of Agricultural Science, Beijing 100081, China
晴空无云条件下,可以利用热红外遥感比较精确地反演地表温度,某些算法精度已经可以达到1 K以内[1-2]。但当地表上空被云层覆盖时,地表的热红外信号将很难穿透云层被传感器捕捉到,即使可以穿透云层(一般仅可穿透高空薄云[3])到达传感器,也势必会受到云层比较严重的影响,难以对地表温度进行比较精确的反演。而据国际卫星云气候计划(the International Satellite Cloud Climatology Project, ISCCP)20多年的持续云观测资料显示,全球陆面总云量均值约为55.9%[4],因此,仅利用热红外遥感数据反演地表温度无法满足实际需求。
与之相比,微波遥感因为波长较长,地表微波信号可以很容易地穿透云层(甚至一定程度的雨区)到达传感器,这为有云条件下地表温度更精确的反演提供了可能。但是大气和云层对微波信号的影响有多大?在地表温度反演过程中能否直接将其忽略?贾媛媛[5]和刘曾林[6]研究晴空无云情况下大气对AMSR-E各通道的影响,结果表明即使无云大气也会对其产生几K到几十K的影响;周芳成等[7]利用与AMSR-E各通道设置相似的FY-3B(“风云三号”B星)传感器得到与之类似的结果。姚志刚和陈洪滨[8]、黄兴有等[9]以及Qiu等[10-12]分别研究云层覆盖时云中液态水对50~60 GHz、22.035~58.8 GHz以及AMSR-E各个通道的影响,结果均表明云中液态水对18.7 GHz及其以上高频通道观测亮温的影响不可忽视(在某些通道的影响甚至达到上百K)。因此选择合适的研究通道,并准确刻画大气和云层信息对该通道微波信号的影响,进而对其进行大气校正,是利用微波遥感数据进行更高精度的地表温度反演的必要前提。
云按照形态可以分成4大类,即积云、雨云、卷云和层云[13]。这4种云类型中,积云厚度往往达数千米,地表微波信号很难穿透;雨云对微波信号的散射作用较强,难以精确模拟;卷云一般由高空中的细小冰晶组成,对微波信号基本没有影响[14-15]。因此本研究将主要分析晴空条件下的层云和云层厚度相对较薄(如信风积云厚度一般为1~2 km,淡积云厚度仅为几百米到1 km[13])的积云对微波信号的影响。同时有研究表明,冰云的吸收系数很小(比水云小几百倍),对微波信号的影响基本可以忽略[14-15],于是本文将云内粒子类型进一步限定为液态小水滴。
晴空有云条件下,大气对微波信号的影响包括两部分,一部分为云层的影响;另一部分为除去云层之外的大气的影响,它等于同等情况下,无云大气的影响。因此本文将以辐射传输方程为理论基础,以TIRG(thermodynamic initial guess retrieval)大气廓线数据库作为研究数据,利用微波辐射传输模型,以理论分析和模型模拟相结合的方式分别对晴空条件下无云大气和云层两种介质对AMSR-E被动微波传感器各通道微波信号的影响进行定量描述,并依此进行地表温度反演算法的可用通道分析,确定合适的通道,为晴空有云条件下较高精度的地表温度反演算法的构建奠定基础。
1 研究数据与辐射传输模型本文将以AMSR-E传感器为研究对象,使用的大气数据为TIGR全球大气廓线数据库,微波辐射传输模型采用MonoRTM(monochromatic radiative transfer model)和CRTM(community radiative transfer model),下面将对TIGR大气廓线和辐射传输模型做进一步的介绍。
1.1 大气廓线数据本研究使用的大气数据是法国动力气象实验室Laboratoire de Meteorologie Dynamique, LMD)的ARA工作组(Atmosphric Radiance Anslysis Group)提供的TIGR廓线数据。该数据共包含2 311条廓线,它们是从全球150 000余组探空数据中精选出来的,涵盖5种大气状况:热带大气、温带大气、寒温带与极地大气、北半球甚极地大气和冬天极地大气。每条廓线从1 013~0.05 hPa共设40个气压级,对应的海拔高度大致为0.02~75 km,其中每个气压层又包含大气温度、湿度、臭氧含量等数据值。由于大约99%的大气重量都处于25~30 km以下的大气层中[16],同时考虑到本文的研究内容,本文只选择30 km以内全球陆地上空的无云晴空廓线(判断条件为:任何气压级相对湿度均大于90%以及相邻气压级相对湿度均大于85%[17-18])作为研究数据。
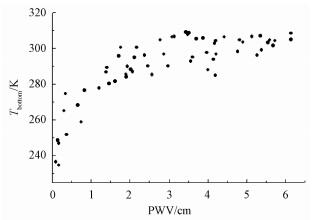
为便于分析研究,本文从筛选出的无云大气廓线中随机抽出60条廓线,其大气可降水量分布在0.09~6.15 cm范围内。图 1为这60条廓线近地表空气温度Tbottom与大气可降水量(precipitable water vaper, PWV)的关系图。从图中可以看到Tbottom分布范围为235~310 K,这基本囊括全球范围内常见的近地表空气温度情况。
|
Download:
|
| 图 1 廓线近地表层空气温度与PWV的关系(60条) Fig. 1 Relationships between PWV and Tbottom based on the 60 selected atmospheric profiles from TIGR | |
MonoRTM可以进行激光、毫米波、微波通道的辐射传输研究,其比较突出的一个优势在于可以利用MODM(monochromatic optical depth model)模块方便地模拟出多种大气分子各自引起的分子光学厚度,即大气中各种分子对入射电磁波的衰减作用[7, 9, 19]。
CRTM是JSCDA(美国卫星资料同化联合中心)开发的一个快速辐射传输模式,可用于紫外、可见光、红外、微波通道的辐射传输研究,其目标是可以实现全天候条件下的卫星资料同化应用,对受云和降水影响的卫星观测模拟计算能力是该模式的一个突出特点。当前CRTM可以处理的云类型包括水云、冰云、雨云、雪云、霰云和雹云6类,其理论基础是通用的Mie理论[20-22]。
2 大气对被动微波信号影响的理论分析微波传感器在低植被地表上空,频率f和入射角θ的情况下,观测到的微波亮温TBp(f, θ)可由3部分组成[23]:①经过大气衰减的地表辐射;②大气上行辐射;③经大气衰减、地表反射、再次经大气衰减的大气下行辐射和宇宙空间辐射。可以表达为
| $ \begin{array}{l} {T_{{\rm{Bp}}}}\left( {f, \theta } \right) = \mathit{\Gamma }\left( {f, \theta } \right){\varepsilon _{\rm{p}}}\left( f \right){T_S} + {T^ \uparrow }\left( {f, \theta } \right) + \\ \left( {1- {\varepsilon _{\rm{p}}}\left( f \right)} \right)\mathit{\Gamma }\left( {f, \theta } \right)\left[{{T^ \downarrow }\left( {f, \theta } \right) + {T_{{\rm{sky}}}}\mathit{\Gamma }\left( {f, \theta } \right)} \right], \end{array} $ | (1) |
式中:εp(f)是地表发射率,TS为地表温度,Tsky为宇宙辐射亮温(通常取定值2.75 K),p为极化方式;Γ(f, θ)、T↑(f, θ)和T↓(f, θ)这3个物理量是大气参数,分别为大气透过率、大气上行辐射亮温和大气下行辐射亮温[24],它们又可以表示为
| $ \mathit{\Gamma }\left( {f, \theta } \right) = {{\rm{e}}^{-\tau \left( {f, \theta } \right)}}, $ | (2) |
| $ \begin{array}{l} {T^ \uparrow }\left( {f, \theta } \right)\sec \theta \int_0^H {T\left( z \right){\kappa _e}\left( {f, z} \right)\exp } (-\tau \left( {f, z, H} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sec \theta ){\rm{d}}z, \end{array} $ | (3) |
| $ \begin{array}{l} {T^ \downarrow }\left( {f, \theta } \right)\sec \theta \int_0^\infty {T\left( z \right){\kappa _e}\left( {f, z} \right)\exp } (-\tau \left( {f, 0, z} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sec \theta ){\rm{d}}z, \end{array} $ | (4) |
式中:T(z)和κe(f, θ)分别为高度z处的分子动力学温度和大气衰减系数;τ(f, θ)为从地表或卫星高度处z1到高度z的路径上大气层的光学厚度,它是衰减系数的函数
| $ \tau \left( {f, \theta } \right) = \int_{{z_1}}^z {{\kappa _e}\left( {f, \theta, z} \right){\rm{d}}z} . $ | (5) |
由式(1)~式(5)可知,大气对微波观测亮温影响的决定性物理量为大气衰减系数κe(f, θ)和大气的分子动力学温度T(z),它们在辐射传输的整个过程中表现为大气透过率,大气上、下行辐射亮温3个物理量。为了更加深入地理解微波穿过大气进入传感器的整个过程中,大气对微波信号的衰减以及其自身的辐射作用。接下来将按照晴空无云大气和非降雨云两种介质,对大气透过率的影响及决定因素做进一步分析;并在此基础上对大气的辐射作用,进行初步探讨。
2.1 晴空无云条件下大气透过率影响因素分析晴空无云条件下,大气对微波信号的衰减主要是由氧气和水汽两种气体分子的吸收所引起,即
| $ {\kappa _e} \approx {\kappa _{{{\rm{O}}_2}}} + {\kappa _{{{\rm{H}}_2}{\rm{O}}}}. $ | (6) |
前者因在大气中的含量相对比较稳定,在某一特定频率下,其对电磁波的衰减作用可以近似为一个常量;而后者是大气中最活跃的因素,无法将其按照前者的方式进行处理,但由于水汽吸收系数κH2O正比于水汽密度[24],而水汽密度又正比于大气可降水量PWV,则结合式(2)、式(5)、式(6)可以得到晴空无云条件下大气透过率与PWV的关系表达式
| $ \begin{array}{l} \mathit{\Gamma = }\exp \left( {-\int_{{z_1}}^z {{\kappa _{{{\rm{O}}_2}}}{\rm{d}}z} } \right) \cdot \exp \left( {-\int_{{z_1}}^z {{\kappa _{{{\rm{H}}_2}{\rm{O}}}}{\rm{d}}z} } \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;U \cdot {{\rm{e}}^{-V \cdot {\rm{PWV}}}}. \end{array} $ | (7) |
式中:U和V为常数,PWV的单位为cm。
2.2 非降雨云条件下大气透过率影响因素分析非降雨情况下,云层对入射电磁波(微波)的衰减主要与云中液态水的吸收作用有关,其对电磁波的总衰减系数[14]可以表示为
| $ {\kappa _{{\rm{cloud}}}} = \frac{{6{\rm{ \mathsf{ π} }}}}{{\lambda \rho }}{\rm{Im}}\left( {-K} \right) \cdot M $ | (8) |
式中:ρ为云中液态水的密度,kg/m3;M为云中液态水含量,kg/m3;λ为入射电磁波的波长,m;K为折射指数的函数,Im(-K)表示取K值的虚部,它与云层的分子动力学温度有关,无量纲。由λ、ρ、M以及Im(-K)的单位可知,总衰减系数的单位为m-1。
式(8)表明,非降雨云对入射电磁波的衰减仅与云中含水量及云层分子动力学温度有关,而与云内粒子的大小或分布无关,这不仅大大简化了云层的微波辐射研究,更奠定了利用云层微波辐射强度信息探测或反演云中含水量的物理基础。
将式(8)代入式(5)可以得到非降雨云云层的光学厚度
| $ {\tau _{{\rm{cloud}}}} = \int_{{H_1}}^{{H_2}} {{\kappa _{{\rm{cloud}}}}{\rm{d}}z}, $ | (9) |
式中:H1、H2分别为云底和云顶的高度。如若假定κcloud中的K值由整个云层的平均温度所决定,则将式(9)代入式(2)可以得到云层对入射电磁波的总透过率
| $ {\mathit{\Gamma }_{{\rm{cloud}}}} = \exp \left( {-\frac{{6{\rm{ \mathsf{ π} }}}}{{\lambda \rho }}{\rm{Im}}\left( {-K} \right) \cdot G} \right) $ | (10) |
式中:G为单位面积云柱中的总含水量,单位kg/m2,按照本文的研究内容它等于云中液态水含量(cloud liquid water, CLW)。
2.3 大气辐射与气体分子和云中液态水的关系由式(3)、式(4)可知,在一定厚度的大气层中,其上、下行辐射亮温主要是天顶角θ、气体衰减系数κe和分子动力学温度T(z)的函数。又由上文分析可知非降雨云情况下,大气对入射电磁波的衰减主要为气体分子和云中液态水的吸收作用,即大气的衰减系数应可以表示为气体分子和云中液态水对微波信号的吸收系数的函数。同时根据普朗克辐射定律和基尔霍夫定律可知在频率一定的情况下,物体的辐射只与其温度有关,物体的辐射越强,吸收也越强,即气体的吸收系数可以用大气的分子动力学温度T(z)进行表示,或者说两个物理量可以相互表示。则当传感器位置确定(即θ取定值)后,大气上、下行辐射亮温便可以仅表示成气体分子和云中液态水对微波信号的吸收系数的函数。
由2.1和2.2节可知,气体分子和云中液态水对微波信号的吸收系数仅与气体分子(氧气和水汽)含量以及云中液态水含量有关,因此,大气的辐射作用也应该与大气中气体分子的含量和云中液态水含量有关,且应为正相关的关系。
3 大气对被动微波信号影响的模拟分析晴空有云条件下,除去云层之外的大气对微波信号的影响等于同等条件下晴空无云大气对微波信号的影响。因此本文从晴空无云和晴空有云两个方面分析大气对AMSR-E微波信号各个通道的影响。
3.1 晴空无云大气对微波信号影响的模拟分析晴空无云情况下,在同等条件下利用MonoRTM和CRTM分别进行辐射传输模拟,发现得到的大气上、下行辐射亮温,大气透过率以及星上亮温存在很好的一致性。由于MonoRTM同时可以方便地模拟出各种大气分子的衰减作用,所以这里以该模型模拟得到的结果进行讨论分析。
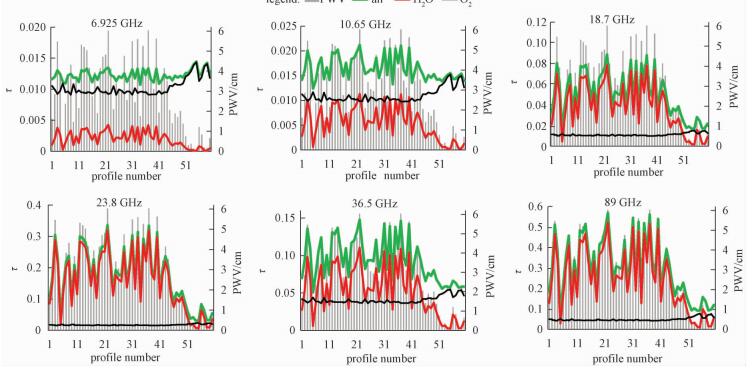
图 2为模拟得到的AMSR-E各个通道里氧气分子、水汽分子和所有的气体分子所引起的光学厚度,该图可以对本文第3节的一些理论基础进行验证和补充:
|
Download:
|
| 图 2 水汽、氧气和所有大气分子在AMSR-E各通道的光学厚度 Fig. 2 Optical depths of H2O, O2, and all gas molecules in the six channels of AMSR-E | |
1) 所有气体引起的光学厚度与氧气和水汽引起的光学厚度之和大致相等,经统计二者之差在6个通道中的最大值仅为0.006 5。这说明晴空无云条件下,氧气和水汽是大气中导致电磁波衰减的主要因素。
2) 6.925和10.65 GHz这2个通道氧气对电磁波的衰减一般比水汽大,且氧气对电磁波的衰减作用在各条廓线之间变化相对较大,不能简单地将其看作常量。而18.7、23.8、36.5和89 GHz这4个通道,正好与之相反,水汽对电磁波的影响更大,且氧气对电磁波的衰减在各条廓线之间相对稳定,可以将其视为常量。
3) PWV值的大小和水汽分子引起的光学厚度以及所有气体分子引起的光学厚度之间存在很好的一致性,这说明PWV的变化可以反映所有大气分子对微波信号的衰减的强弱,即无云大气对微波信号的衰减可以表示成大气可降水量的函数。
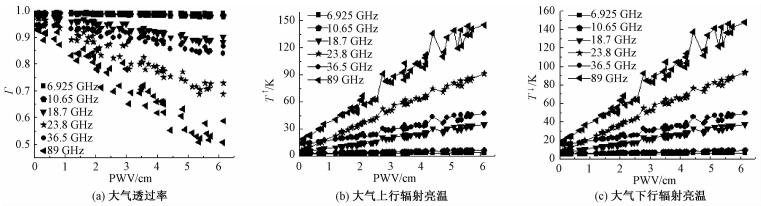
根据结论3)以及理论基础部分的表述将模拟得到的大气透过率,以及大气上、下行辐射亮温按照PWV的大小进行显示,如图 3。
|
Download:
|
| 图 3 大气透过率,大气上、下行辐射亮温和大气可降水量的关系 Fig. 3 Relationships of PWV with atmospheric transmittance, upwelling atmospheric brightness temperature, and downwelling atmospheric brightness temperature | |
分析图 3可知:
1) 6.925和10.65 GHz这2个通道,大气透过率基本不随PWV的变化而变化,且其值始终接近于1;上、下行辐射亮温变化也不大,且数值较小(6.925 GHz通道最大值3.9 K,10.65 GHz通道最大值6.2 K),说明在这2个通道大气对入射电磁波的衰减以及大气自身的辐射作用都比较小,可以忽略大气的影响。
2) 18.7、23.8、36.5、89 GHz这4个通道大气透过率与PWV近似成反比关系,大气上、下行辐射亮温与PWV近似成正比关系。且从变化速率上来看,18.7≈36.5 < 23.8 < 89 GHz,这说明PWV对18.7和36.5 GHz这2个通道的影响相当,另外2个通道相比于这2个通道依次增大。查阅资料[25]可知,造成23.8 GHz通道比36.5 GHz通道受PWV影响更大的原因是23.8 GHz通道处在水汽(气态水)吸收带上。
3) 为了更直观地分析大气对18.7、23.8、36.5和89 GHz这4个通道的影响,本文统计了模拟数据结果中大气透过率的最小值和大气上、下行辐射亮温的最大值(来自于一条廓线,其PWV值为6.15 cm)如表 1。可以看到,在该条件下,这4个通道都受到大气比较大的影响,以直接进入传感器的大气上行辐射亮温(T↑)为例,即使受影响最小的18.7 GHz通道,其值也超过30 K。如若不考虑大气信息的影响,则星上亮温便有了>30 K的偏差,这势必会对地表温度反演的实际精度造成很大的影响。因此,在高精度的被动微波地表温度反演算法的构建过程中,即使晴空无云情况下,这4个通道也不能忽略大气对微波信号的影响,即不能忽略无云大气对微波信号的影响。
|
|
表 1 AMSR-E后4个通道最小大气透过率、最大大气上行和下行辐射亮温 Table 1 Minimum value of atmosphere transmittance and maximum values of upwelling and downwelling brightness temperatures in the last four channels of AMSR-E |
晴空有云情况下的辐射传输模拟使用的是CRTM辐射传模型,云层参数按照本文的研究内容以及参考文献[13-14, 21-22, 26-28],将其指定为:云中含水类型water_cloud;云中含水量0.0~0.70 kg/m2,步长0.01 kg/m2;云粒子大小15 μm;云层高度1~2 km。同时为了尽可能地突出云层信息对微波信号的影响,本研究选取的大气廓线为筛选的60条廓线中大气可降水量最小的一条廓线,其PWV=0.09 cm。
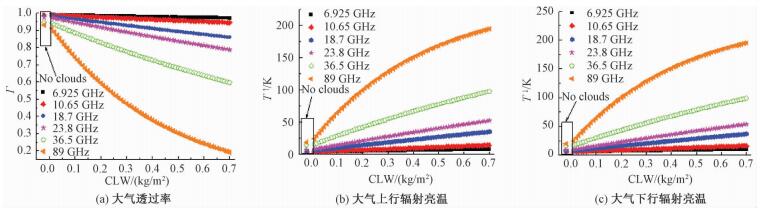
根据理论基础部分分析可知非降雨云对微波信号的影响,可以表示成云中含水量的函数,因此这里将得到的大气透过率和上、下行辐射亮温按照云中液态水含量CLW的大小进行显示,如图 4。
|
Download:
|
| 图 4 大气透过率,大气上、下行辐射亮温和云中液态水的关系 Fig. 4 Relationships of CLW with atmospheric transmittance, upwelling atmospheric brightness temperature, and downwelling atmospheric brightness | |
分析图 4可知:
1) 6.925、10.65 GHz这2个通道的大气透过率和上、下行辐射亮温随云中液态水含量的增加,几乎没有变化,即这2个通道基本不受云层信息的影响。
2) 云层对18.7、23.8、36.5和89 GHz这4个通道的影响都是随着CLW的增大而逐渐增大,且从增大的“速率”上来看,18.7 < 23.8 < 36.5 < 89 GHz,即云层对这4个通道的影响,依次增强。
3) 云中液态水含量较小时6.925、10.65、18.7和23.8 GHz这4个通道受云层影响不易区分,且随CLW的增大,18.7和23.8 GHz这2个通道受云层的影响也比较接近。
4) 与同等情况下无云大气相比,18.7、23.8、36.5和89 GHz这4个通道,随着CLW的增大,受大气的影响都有明显的增加。且图 3和图 4对比可以发现,云中液态水对微波信号的影响要比大气可降水量的影响更大。因此,在高精度的被动微波地表温度反演算法的构建过程中,这4个通道更不能忽略云层信息对微波信号的影响。
3.3 地表温度反演通道的选择通过3.1和3.2节的分析可知,6.925和10.65 GHz这2个通道基本不受大气和云层的影响。但由于其波长较长,穿透能力强,在地表温度反演时,一般反演得到的是一定地表厚度的综合温度,并非严格意义上的地表温度;并且由于这2个通道受到低频段无线电干扰(radio frequency interference, RFI)影响较为严重[29-30],所以一般在地表参数定量反演中,都避免选用这2个通道,因此本文也暂且不对其进行考虑。
对图 4进一步分析可知,相比于其他通道,89 GHz通道受云层的影响较大。以大气透过率为例,当CLW=0.7 kg/m2时,该通道的透过率仅为0.192,这表明可以透过云层进入传感器的地表信息非常少,因此该通道难以用来进行有云情况下地表温度算法的构建。
18.7、23.8和36.5 GHz这3个通道虽然也不能忽略大气和云层的影响,但它们所受影响相对较小。且据3.1和3.2节分析可知,18.7、36.5 GHz这2个通道受PWV的影响相当,其中18.7 GHz通道受大气总的影响更小。而23.8 GHz相比于这2个通道,受到PWV的影响稍大,因此可以利用18.7、23.8 GHz这2个通道研究水汽分子的影响,即除去云层之外的大气的影响。同样的原理,可以利用18.7和36.5 GHz这2个通道研究云层信息的影响。因此本研究决定将18.7、23.8和36.5 GHz这3个通道定为接下来构建有云情况下较高精度地表温度反演算法的预选通道。
4 结论以理论分析和模型模拟相结合的方式研究晴空有云大气对AMSR-E各通道微波信号的影响,结果表明:
1) 无云大气对微波信号的影响主要与氧气和水汽有关;云层对微波信号的影响主要与云中液态水有关。
2) 18.7, 23.8, 36.5和89 GHz这4个通道受无云大气的影响可以表示成大气可降水量PWV的函数;云层对这4个通道的影响可以表示成云中液态水CLW的函数。
3) 6.925、10.65 GHz这2个通道基本不受云层和无云大气的影响。18.7、23.8和36.5 GHz这3个通道,在高精度的地表温度反演算法的构建过程中必须考虑云层和无云大气的影响。89 GHz通道在AMSR-E的6个通道中受到的影响最大,且当云中液态水较大时,穿过云层进入传感器的地表信号将非常少。
4) 大气可降水量对18.7和36.5 GHz这2个通道的影响作用大小相当,而18.7 GHz受大气总的影响更小;23.8 GHz相比于这2个通道,受到大气可降水量的影响更大。云层对18.7、23.8和36.5 GHz这3个通道的影响依次增大,而18.7和23.8 GHz这2个通道受云层的影响相差不大,不易区分。
在以上结论的基础上,通过进一步分析,本文选出18.7、23.8和36.5 GHz这3个通道作为接下来构建较高精度的被动微波地表温度反演算法的预选通道。同时定量分析无云大气和云层对微波信号的具体影响方式及大小,这为非降雨云条件下或晴空无云条件下利用被动微波数据反演地表参数时如何进行大气校正指明了方向,也奠定了理论基础。
| [1] |
徐希孺, 陈良富, 庄家礼. 基于多角度热红外遥感的混合像元组分温度演化反演方法[J]. 中国科学:地球科学, 2001, 31(1):81–88.
|
| [2] |
Wan Z, Zhang Y, Zhang Q, et al. Quality assessment and validation of the MODIS global land surface temperature[J]. International Journal of Remote Sensing, 2004, 25(1):261–274.
DOI:10.1080/0143116031000116417 |
| [3] |
范熙伟. 考虑气溶胶和高空薄云影响的地表温度反演方法研究[D]. 北京: 中国科学院地理科学与资源研究所, 2015.
http://d.g.wanfangdata.com.cn/Thesis_Y2958320.aspx |
| [4] |
刘奇, 傅云飞, 冯沙. 基于ISCCP观测的云量全球分布及其在NCEP再分析场中的指示[J]. 气象学报, 2010, 68(5):689–704.
DOI:10.11676/qxxb2010.067 |
| [5] |
贾媛媛. 被动微波遥感数据反演地表温度算法研究[D]. 北京: 中国科学院地理科学与资源研究所, 2007.
http://www.irgrid.ac.cn/handle/1471x/145282 |
| [6] |
刘曾林. 被动微波遥感地表温度算法研究[D]. 北京: 中国科学院地理科学与资源研究所, 2013.
http://d.wanfangdata.com.cn/Thesis/Y2431633 |
| [7] |
周芳成, 宋小宁, 李召良, 等. 微波遥感定量反演研究中大气参数的估算模型[J]. 中国科学院大学学报, 2015, 32(1):63–69.
|
| [8] |
姚志刚, 陈洪滨. 七通道微波辐射计遥感大气温度廓线的性能分析[J]. 气象科学, 2005, 25(2):133–141.
|
| [9] |
黄兴友, 张曦, 冷亮, 等. 基于MonoRTM模型的微波辐射计反演方法研究[J]. 气象科学, 2013, 33(2):138–145.
DOI:10.3969/2012jms.0127 |
| [10] |
Qiu Y, Shi J, Jiang L, et al. Study of atmospheric effects on AMSR-E microwave brightness temperature over Tibetan Plateau[C]//Geoscience and remote sensing symposium, 2007. IGARSS 2007. IEEE International. IEEE, 2007: 1873-1876.
http://ieeexplore.ieee.org/document/4423189/citations |
| [11] |
Qiu Y, Shi J, Lemmetyinen J, et al. The Atmosphere influence to AMSR-E measurements over snow-covered areas: simulation and experiments[C]//Geoscience and Remote Sensing Symposium, 2009 IEEE International, IGARSS 2009. IEEE, 2009, 2: Ⅱ-610-Ⅱ-613.
http://ieeexplore.ieee.org/document/5418158/ |
| [12] |
邱玉宝. 陆面被动微波遥感大气影响分析与校正研究[D]. 北京: 中国科学院遥感与数字地球研究所, 2008.
http://www.irgrid.ac.cn/handle/1471x/823528 |
| [13] |
王伟民, 刘华强, 王桂玲, 等.
大气科学基础[M]. 北京: 气象出版社, 2011.
|
| [14] |
周秀骥.
大气微波辐射及遥感原理[M]. 北京: 科学出版社, 1982.
|
| [15] |
邱玉宝, 石利娟, 施建成, 等. 大气对星载被动微波影响分析研究[J]. 光谱学与光谱分析, 2016, 36(2):310–315.
|
| [16] |
刘本培, 蔡运龙.
地球科学导论[M]. 北京: 高等教育出版社, 2000.
|
| [17] |
Galve J M, Coll C, Caselles V, et al. An atmospheric radiosounding database for generating land surface temperature algorithms[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(5):1547–1557.
DOI:10.1109/TGRS.2008.916084 |
| [18] |
Wu H, Ni L, Wang N, et al. Estimation of atmospheric profiles from hyperspectral infrared IASI sensor[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013, 6(3):1485–1494.
DOI:10.1109/JSTARS.2013.2258138 |
| [19] |
车云飞, 马舒庆, 杨玲, 等. 云对地基微波辐射计反演湿度廓线的影响[J]. 应用气象学报, 2015(2):193–202.
DOI:10.11898/1001-7313.20150207 |
| [20] |
白翎, 师春香, 刘冰, 等. CRT M微波亮温模拟对地表和云参数的敏感性分析[J]. 气象, 2014, 40(11):1363–1371.
DOI:10.7519/j.issn.1000-0526.2014.11.009 |
| [21] |
董佩明, 王海军, 韩威, 等. 水物质对云雨区卫星微波观测模拟影响[J]. 应用气象学报, 2009, 20(6):682–691.
DOI:10.11898/1001-7313.20090605 |
| [22] |
顾成明, 王云峰, 张晓辉, 等. 云参数对微波亮温模拟计算的影响试验[J]. 应用气象学报, 2016, 27(3):380–384.
DOI:10.11898/1001-7313.20160313 |
| [23] |
Kerr Y H, Njoku E G. A semiempirical model for interpreting microwave emission from semiarid land surfaces as seen from space[J]. IEEE Transactions on Geoscience and Remote Sensing, 1990, 28(3):384–393.
DOI:10.1109/36.54364 |
| [24] |
Ulaby F T, Moore R K, Fung A K.
Microwave remote sensing Ⅰ:fundamentals and radiometry[M]. Addison-Wesley Publishing Company, 1981.
|
| [25] |
赵英时.
遥感应用分析原理与方法[M]. 北京: 科学出版社, 2013.
|
| [26] |
盛裴轩, 毛节泰, 李建国, 等.
大气物理学[M]. 北京: 北京大学出版社, 2003.
|
| [27] |
王明康.
云和降水物理学[M]. 北京: 科学出版社, 1991.
|
| [28] |
顾震潮.
云雾降水物理基础[M]. 北京: 科学出版社, 1980.
|
| [29] |
Li L, Njoku E G, Im E, et al. A preliminary survey of radio-frequency interference over the US in Aqua AMSR-E data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(2):380–390.
DOI:10.1109/TGRS.2003.817195 |
| [30] |
Njoku E G, Ashcroft P, Chan T K, et al. Global survey and statistics of radio-frequency interference in AMSR-E land observations[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(5):938–947.
DOI:10.1109/TGRS.2004.837507 |
 2018, Vol. 35
2018, Vol. 35 


