2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
卫星通信是利用通信卫星作中继站实现的微波中继通信方式。对于军事及低速率、小容量的卫星通信系统,通常采取码分多址(CDMA)扩频通信体制。CDMA具有抗干扰能力强、信号功率谱密度较小、隐蔽性好的优点。但是卫星通信系统受制于传输损耗和移动远端站天线增益等因素,信号较为微弱。在微弱信号条件下,CDMA系统接收机对伪随机码的同步较为困难。为提高接收机灵敏度,通常采取延长相干积分时间和增加非相干积分次数的方法[1]。但在确定电文比特边界即位同步的环节,由于电文比特存在0、1翻转,相干积分不能跨电文比特,所以积分时间长度受限制[2]。而由于非相干积分损耗的存在,非相干积分次数也不能太多。因此,位同步门限成为制约接收灵敏度的瓶颈。文献[3]提出直方图算法,通过统计某一位置数据符号变化的次数判断数据符号翻转,但在信号微弱条件下位同步成功概率较低。文献[4]使用Viterbi算法进行比特翻转边界估计,在微弱信号条件下性能较好,但计算量较大。Kokkonen和Pietil[5]提出K-P法:计算出不同起始位置一个比特长度的积分结果,结果最大的起始位置即为翻转位置,该方法在微弱信号条件下位同步准确概率较直方图法大大提高,但对频率偏差敏感。Li和Guo[6]提出一种差分位同步算法,采用相邻积分结果差分相干的方法消除频率偏差的影响,但是差分相干会造成噪声的增加,从而降低位同步成功概率。以上一系列位同步算法,通过积分结果估计电文比特跳变沿,没有从根本上摆脱积分时间和频率偏差的制约,限制了位同步性能的提高或者需要较大的运算量开销。本文提出一种基于卫星导航授时的间接时间同步方法,使接收端在时间同步信号的辅助下准确地得到伪码和电文比特的起始边沿,在确定时刻直接进行伪码相关和电文解调,省去位同步环节,从而消除系统的位同步瓶颈。
利用卫星导航授时修正本地时钟获得高精度时钟(“驯服”)和通过时间传递技术实现时间同步的方法国内外已经进行了深入的研究:文献[7-8]利用GPS时钟长期稳定度较好的特性结合高稳晶振或芯片级原子钟短期稳定度较好的优点实现GPS驯服晶振; 文献[9]研究基于锁相环结构的钟差校准方法,实现了本地时钟钟差校准。以上方法只针对本地时钟的校准,从而获得高精度本地时钟或使本地时钟与卫星导航授时系统的时间同步。对于通信系统,由于存在传输时延,尤其是卫星通信,在信号传播过程中需经上行及下行两个链路,传输时延较大,产生误差的环节较多(卫星漂移、设备时延、处理时延等),仅仅建立本地时间与卫星导航授时系统时间的同步,发送的信号经星地链路到达接收端的具体时刻仍是一个不确定的量,还需对多个环节的传播时间误差进行修正,否则利用卫星导航授时直接同步本地时钟的方案无法直接用于扩频信号伪码的同步。
本文基于GNSS(Global Navigation Satellite System, 全球卫星导航系统)卫星导航授时提出的通过星地自发自收链路(地面站—卫星—地面站)实现的卫星通信系统前向链路(地面站—卫星—远端站)间接时间同步方法,其基本原理是:通过由星地自发自收链路与锁相环构成的钟差间接修正环路,对地面站发送时钟进行闭环修正,地面站发送的扩频信号起始码相位在到达远端站时与卫星导航授时模块输出的秒脉冲(1 PPS, 1 pulse per second)保持精确稳定的同步,同步误差限定在1/2扩频码片以内。同时由于地面站天线口径较大、增益较高,地面站自发自收链路采取较小的发射功率即可获得较高的接收信噪比,可以提供稳定可靠的高精度时间同步。以下首先介绍间接时间同步方法基本原理和实现模型,然后针对钟差间接修正环路模型、环路误差组成、最佳环路带宽值选取作重点讨论,最后通过星地链路进行试验验证。
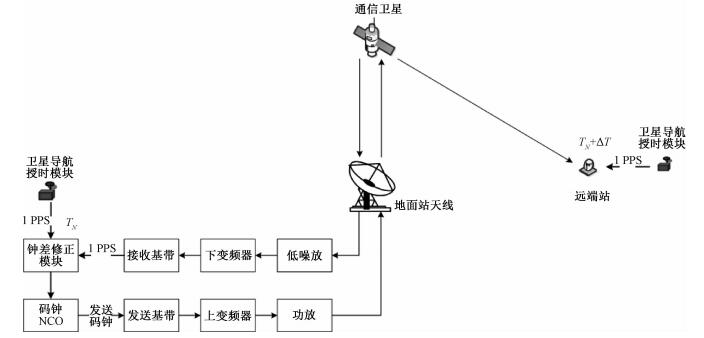
1 钟差间接修正环路对于“地面站—卫星—远端站”组成的前向通信链路,在地面站设置钟差修正模块,同时通过收发基带、地面站射频收发设备(上、下变频器、低噪放、功放和天线)以及通信卫星构成地面站自发自收链路,从而实现前向链路的间接时间同步,如图 1所示。
|
Download:
|
| 图 1 前向链路间接时间同步原理框图 Fig. 1 Block diagram of indirect time synchronization in forward link | |
前向链路的间接时间同步的具体原理如下:卫星导航授时模块定位之后在每个整秒TN时输出1 PPS信号作为整秒时间基准,地面站经过星地链路进行自发自收闭环,发送基带发送同步电文(1帧/s),接收基带在接收电文帧起始码相位处生成一个1 PPS,比较2个1 PPS的秒相位差,通过钟差修正模块对发送端码钟NCO(numerically controlled oscillator,数字控制振荡器)进行调整,间接修正到达接收端的帧起始码相位,使之逐渐与授时系统的1 PPS同步并保持跟踪。
地面站自发自收链路同步完成之后,对于“地面站—卫星—地面站”链路和“地面站—卫星—远端站”链路,二者上行链路及卫星转发器时延均相同,仅卫星下行链路不同,因此减少了传播时间误差修正环节。地面站广播的信号从卫星下行到达远端站与地面站的时间差ΔT可以由远端站根据自身定位结果、地面站坐标、卫星轨道精确预报信息[10]、C波段电离层传播延迟误差[11]和硬件延迟误差[12-13]进行精确计算标定。
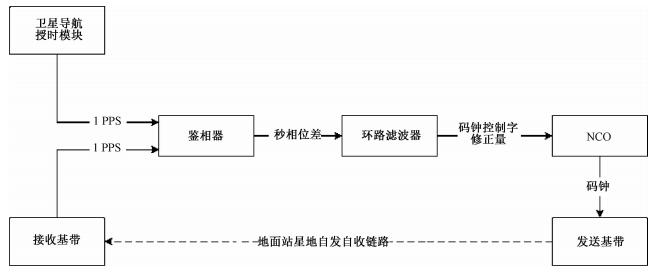
图 1中的钟差修正模块与地面站星地收发链路共同构成钟差间接修正环路。钟差间接修正环路采取锁相环结构,如图 2所示:鉴相器以高频时钟(100 MHz)对授时模块和接收基带输出的两路1 PPS的上升沿进行采样、记录并计算两路1 PPS的时间差作为秒相位差输出至环路滤波器,滤除高频噪声之后以DDS(direct digital synthesizer, 数字频率合成器)方式调节发送基带码钟NCO,带动接收基带的时钟调整,实现对接收基带时钟的间接修正,最终使接收基带输出的1 PPS振荡逼近授时模块输出的1 PPS并保持跟踪。
|
Download:
|
| 图 2 钟差间接修正环路原理框图 Fig. 2 Block diagram of indirect clock correction loop | |
用DDS方式调节本地发送码时钟原理如下
| $ f + \Delta f = \frac{{{\rm{FTW}} + \Delta {\rm{FTW}}}}{{{2^N}}} \cdot {f_{{\rm{sys}}}}, $ | (1) |
式中:f为码钟固有速率;Δf为码钟速率修正量;FTW为码钟固有控制字;ΔFTW为码钟控制字修正量;N为相位累加器长度;fsys为系统驱动时钟。
鉴相器对1 PPS秒相位差的测量时的噪声误差,需要通过环路滤波器进行滤波处理。环路滤波器对环路动态特性和跟踪精度有重要影响。环路带宽BL是环路滤波器设计的重要参数,其取值对环路跟踪性能有重要影响。通常情况下,环路带宽越窄,对热噪声滤除效果越好,频率估计精度越高,但动态性能较差,且频率捕获时间较长;环路带宽越宽,动态性能越好,但热噪声误差较大。同时晶振阿伦方差产生的颤动通过环路时也受到环路带宽的约束。对于晶振而言,环路带宽越大,对于滤除阿伦方差产生的晶振噪声越有利[14]。因此,环路带宽的取值应综合以上多种因素考虑。
2 钟差间接修正环路误差分析 2.1 间接修正环路总误差经典锁相环环路1σ误差经验公式[9]如下
| $ {\sigma _{{\rm{PLL}}}} = \sqrt {\sigma _{t{\rm{PLL}}}^2 + \theta _{\rm{A}}^2 + \sigma _{\rm{v}}^2} + \frac{{{\theta _{\rm{e}}}}}{3}, $ | (2) |
式中:σtPLL表示鉴相器1σ热噪声造成的跟踪误差;θA表示由阿伦方差引起的晶振颤动;σv表示由振动引起的1σ晶振颤动;θe表示跟踪环路的动态应力误差。
对于由振动引起的1σ晶振颤动σv,由晶振本身特性决定,不在本文讨论范围。同时,由于钟差修正模块位于地面站,且同步卫星漂移较小,二者可以认为是相对静止的,所以由载体运动造成的动态应力误差θe为0。因此,式(2)可写为
| $ {\sigma _{{\rm{PLL}}}} = \sqrt {\sigma _{t{\rm{PLL}}}^2 + \theta _{\rm{A}}^2} . $ | (3) |
对于图 2所示的间接修正环路模型,在原锁相环模型中增加了一个地面站自发自收链路。自发自收链路中收发基带之间存在码相位跟踪误差σTR。鉴相器热噪声误差σtPLL、晶振阿伦方差θA和自发自收链路码相位跟踪误差σTR相互独立。因此,间接修正环路1σ总误差σI_PLL为
| $ {\sigma _{{\rm{I\_PLL}}}} = \sqrt {\sigma _{t{\rm{PLL}}}^2 + \theta _{\rm{A}}^2 + \sigma _{{\rm{TR}}}^2} . $ | (4) |
下面针对式(4)中的各项误差做具体分析。
2.2 热噪声误差环路跟踪可以看作一个平稳随机过程,对于平稳随机过程,随机信号的方差等于其交流功率。因此,由鉴相器热噪声造成的1σ热噪声误差σtPLL2等于热噪声通过环路滤波器后输出的交流功率Pno(f),即
| $ \sigma _{t{\rm{PLL}}}^2 = {P_{{\rm{no}}}}\left( f \right) = \int_{ - \infty }^\infty {{S_{{\rm{no}}}}\left( f \right){\rm{d}}f}, $ | (5) |
Sno(f)为热噪声通过环路滤波器后输出的功率谱密度[15]
| $ {S_{{\rm{no}}}}\left( f \right) = {\left| {H\left( f \right)} \right|^2}{S_{{\rm{nd}}}}\left( f \right), $ | (6) |
H(f)为环路滤波器传输函数。Snd(f)为鉴相器输出至环路滤波器的热噪声功率谱密度[15]
| $ {S_{{\rm{nd}}}}\left( f \right) = \sigma _{{\rm{nd}}}^2T\sin {c^2}\left( {fT} \right), $ | (7) |
σnd2为鉴相器热噪声方差;T为环路校正间隔,与秒相位差输出周期相同,由于秒相位差每秒钟输出一次,因此T取为1 s。
对秒脉冲进行相位差测量时,鉴相器热噪声存在两种误差因素:作为基准的授时模块秒脉冲自身的同步误差σs以及鉴相时钟分辨力误差σq。授时模块秒脉冲同步误差由其授时精度决定;鉴相器分辨力误差由鉴相时钟频率决定。二者互不相关,根据随机误差合成理论,鉴相器热噪声方差可通过下式计算:
| $ \sigma _{{\rm{nd}}}^2 = \sigma _{\rm{s}}^2 + \sigma _{\rm{q}}^2, $ | (8) |
σs为授时模块秒脉冲自身1σ同步误差,由授时模块本身性能决定。
鉴相器对1 PPS测量时由鉴相时钟步长(tclk)引起的分辨力误差服从均匀分布,概率密度函数为
| $ \sigma _{\rm{q}}^2 = \frac{1}{{{t_{{\rm{clk}}}}}}\int_{ - \frac{{{t_{{\rm{clk}}}}}}{2}}^{\frac{{{t_{{\rm{clk}}}}}}{2}} {{x^2}{\rm{d}}x} = \frac{1}{{12}}{\left( {{t_{{\rm{clk}}}}} \right)^2} = \frac{1}{{12}}{\left( {\frac{1}{{{f_{{\rm{clk}}}}}}} \right)^2}\left( s \right), $ | (9) |
其中,fclk为秒脉冲鉴相时钟频率。
结合式(5)~式(9),可得
| $ \sigma _{t{\rm{PLL}}}^2 = \int_{ - \infty }^\infty {{{\left| {H\left( f \right)} \right|}^2}\left( {\sigma _{\rm{s}}^2 + \sigma _{\rm{q}}^2} \right)T\sin {c^2}\left( {fT} \right){\rm{d}}f}, $ | (10) |
式中,
| $ \begin{array}{*{20}{c}} {\sigma _{t{\rm{PLL}}}^2 = 2\left( {\sigma _{\rm{s}}^2 + \sigma _{\rm{q}}^2} \right)T\left[{\frac{1}{2}\int_{-\infty }^\infty {{{\left| {H\left( f \right)} \right|}^2}{\rm{d}}f} } \right]}\\ {2\left( {\sigma _{\rm{s}}^2 + \sigma _{\rm{q}}^2} \right)T{B_{\rm{L}}}.} \end{array} $ | (11) |
经过二阶环后,阿伦方差引起的晶振颤动θA[9]为
| $ {\theta _{\rm{A}}} = \frac{2}{5} \cdot \frac{{{\sigma _{\rm{A}}}}}{{{B_{\rm{L}}}}}\left( {\rm{s}} \right), $ | (12) |
式中,σA表示晶振短期阿伦方差。
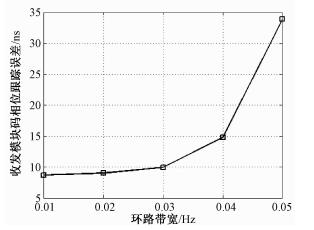
2.4 自发自收链路码相位跟踪误差σTR为自发自收链路中收发基带之间的码相位跟踪误差,与接收载噪比及发送端码钟动态有关。根据图 2所示的间接修正环路结构,在地面站星地自发自收链路接收载噪比一定的情况下,发送端码钟动态由环路滤波器中的参数环路带宽BL值决定:环路带宽BL越大,环路滤波器输出的码钟控制字修正量越大,则码钟调整幅度越大,导致发送码钟动态和码相位跟踪误差σTR越大。为了得出码相位跟踪误差σTR与环路带宽BL的关系,将收发基带直接对接,测量不同环路带宽BL下接收机的码相位跟踪误差σTR。根据图 1中的星地链路实测结果,地面站接收载噪比为45 dB·Hz,因此收发基带直接对接时接收端载噪比也同样设置为45 dB·Hz。测试结果如图 3所示。
|
Download:
|
| 图 3 收发模块基带中频对接测试的码相位跟踪误差 Fig. 3 Code phase tracking error in the tests of intermediate frequency coupled transceiver baseband modules | |
根据测量结果,对σTR与BL的关系表达式通过最小二乘法进行二次函数拟合,得到收发基带之间的码相位跟踪误差σTR与钟差修正环路环路带宽BL近似为如下关系:
| $ \begin{array}{*{20}{c}} {{\sigma _{{\rm{TR}}}} = aB_{\rm{L}}^2 + b{B_{\rm{L}}} + c\left( {{\rm{ns}}} \right), }\\ {a = 3.0 \times {{10}^4}, b = - 1.2 \times {{10}^3}, {c_2} = 20.} \end{array} $ | (13) |
结合式(4)、(8)、(11)、(12)、(13),得到间接修正环路1σ总误差
| $ \begin{array}{*{20}{c}} {{\sigma _{{\rm{I\_PLL}}}} = }\\ {\sqrt {\sigma _{{\rm{TR}}}^2 + 2\left( {\sigma _{\rm{S}}^2 + \sigma _{\rm{q}}^2} \right)T{B_{\rm{L}}} + {{\left( {\frac{2}{5} \cdot \frac{{{\sigma _{\rm{A}}}}}{{{B_{\rm{L}}}}}} \right)}^2}} \left( {{\rm{ns}}} \right).} \end{array} $ | (14) |
在式(14)中相关参数确定之后,将式(14)对BL求导,令其导数等于0,利用matlab求解方程,即可求得使环路总误差最小的环路带宽。
3 星地链路试验验证通过由图 1中同步通信卫星、地面站射频收发设备(上、下变频器、低噪放、功放和天线)、卫星导航授时模块和收发基带构成的星地链路试验平台对地面站自发自收间接同步方法进行试验验证。卫星为中国自行研制的中星20号退役同步通信卫星。地面站射频及天线设备位于天津武清的中国科学院国家天文台导航通信中心站。卫星导航授时模块采用Trimble公司的ResolutionT GPS导航授时模块。收发基带自行研制:接收基带基于Numen导航专用芯片实现;发送基带基于FPGA+DDS芯片实现,具体通信技术指标为:BPSK调制,伪码速率4 Mcps,中频输出为20 MHz。钟差修正模块基于FPGA实现,集成在发送基带中。ResolutionT GPS导航授时模块1 PPS 1σ授时精度σs为15 ns。每个秒脉冲观测校正一次,钟差修正环路校正周期T为1 s,秒脉冲鉴相时钟fclk为100 MHz。参考时钟为10 MHz温补晶振(TCXO),短期阿伦偏差σA为1×10-9。
在以上条件下,根据上述推导计算得最优环路带宽BL为0.03 Hz。
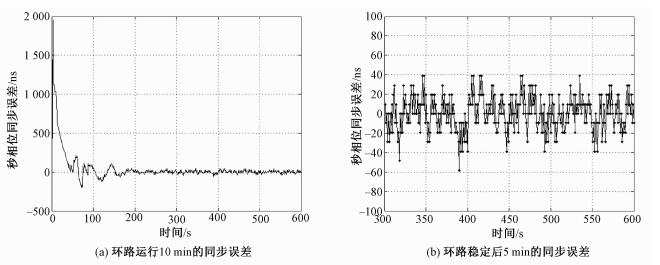
当环路带宽为0.03 Hz时,在上述测试条件下,鉴相器输出的接收基带1 PPS与GPS授时模块1 PPS的同步误差测试结果如图 4所示:图中横轴为时间,纵轴为鉴相器输出的秒相位1σ同步误差。图 4(a)给出环路开始工作后10 min的误差测量结果,经过间接修正环路校正后的秒相位差是一个振荡收敛的过程,从环路开始调整经过3 min左右环路逐渐收敛。图 4(b)是图 4(a)中环路达到稳定后5 min的实测结果的放大图,根据图 4(b)中的实测结果可以得到,接收基带输出的1 PPS与GPS授时模块1 PPS秒相位1σ同步误差σI_PLL约为20 ns。
|
Download:
|
| 图 4 环路带宽为0.03 Hz时的1 PPS同步误差 Fig. 4 PPS synchronization error at loop bandwidth of 0.03 Hz | |
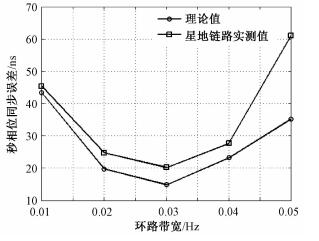
在相同的星地链路测试条件下,令间接同步环路在环路带宽取不同的值时进行工作,统计环路进入稳态之后5 min左右的测试结果。接收基带1 PPS与GPS授时模块1 PPS的秒相位1σ同步误差如图 5所示。当环路带宽取最优值0.03 Hz时,环路同步误差最小,秒相位1σ同步误差σI_PLL约为20 ns;当环路带宽值过大或过小时,秒相位同步误差都较大。星地链路试验结果与理论分析得到的变化趋势基本一致。
|
Download:
|
| 图 5 不同环路带宽下的1 PPS同步误差 Fig. 5 1 PPS synchronization errors at different loop bandwidths | |
同时,由图 5可见,当环路带宽小于0.04 Hz时,实测结果与理论值存在一个固定的偏差,且随着环路带宽的增加,实测值与理论值的偏差有增大的趋势。
造成以上现象的原因可以从以下两方面进行分析:
一方面,在环路滤波器设计时,首先通过双线性变换[14]将环路滤波器传递函数由模拟域函数转换为数字域函数,以便于数字实现。本文中的二阶数字环路滤波器基于FPGA实现,传递函数系数运算时的小数相乘运算通过寄存器移位近似实现,由此会导致环路滤波器输出与理论计算值存在偏差。同时,随着环路带宽增大,近似值与理论计算值的偏差会增大。
另一方面,根据数字锁相环相关理论[16],由模拟域转换为数字域的双线性变换过程中,环路带宽BL与积分时间Tcoh的乘积存在一个临界点,当BLTcoh < 0.1时,模拟环路与数字环路的上述替换对环路带宽的影响较小;随着BLTcoh值的增大,数字环路带宽与模拟环路带宽之间的偏移越来越大,导致数字环路会趋于不稳定。本文中的环路针对秒脉冲进行调整,积分时间Tcoh为1 s,环路带宽增大至0.05 Hz时即出现了实测偏差较理论值有明显增大的趋势。
在上述的间接时间同步环路的辅助下,进行前向链路的扩频通信试验。首先对“卫星—地面站”和“卫星—远端站”两条下行链路通过1 PPS比对得到两个链路到达码相位的固定误差,只剩下间接同步环路的随机误差。根据上文推导及测试结果,到达码相位差的1σ随机误差为20 ns。而试验中的通信扩频码码片宽度为250 ns,1 PPS同步误差远小于扩频码码片宽度。测试结果表明:在1 PPS信号的同步残留20 ns随机误差条件下,通过GPS授时模块输出的1 PPS的触发,接收机直接进入跟踪环路进行码相位的跟踪,并解调出电文数据,省去位同步过程,从而消除了系统位同步瓶颈。
4 结论针对同步卫星扩频通信系统解决位同步门限瓶颈和时间同步的需求,提出一种基于卫星导航授时的卫星扩频通信前向链路间接时间同步方法。在地面站和卫星之间建立“地面站—卫星—地面站”星地自发自收链路,通过由星地自发自收链路和锁相环构成的钟差间接修正环路对地面站发送码时钟以DDS方式进行闭环修正。在间接修正环路作用下,地面站发送的扩频信号起始码相位通过地面站自发自收链路在到达接收端时与卫星导航授时系统1 PPS保持精确稳定的同步。通过分析鉴相器热噪声、时钟阿伦方差、收发链路码相位跟踪误差等环路误差因素,给出总的环路时间同步误差表达式。通过理论计算和试验标定得出环路时间同步误差与环路带宽值的关系,给出使环路总的同步误差最小的最优环路带宽值的选取方法,并通过实际星地链路进行了试验验证。试验结果表明:时间同步误差随环路带宽的变化关系与理论分析一致,最佳环路带宽对应的钟差间接修正环路秒脉冲1σ同步误差约为20 ns,可以保证伪码的同步并完成电文解调,从而实现了卫星导航授时对CDMA扩频通信的辅助,为小容量和突发卫星通信提供了一种新的解决方案。
同时也看到,当环路带宽增大时,秒相位同步误差增加较快,对于高动态卫星通信链路,失锁概率可能会增加,此问题值得进一步深入研究。
感谢国家天文台金声震老师的指导和宝贵建议!| [1] |
JAMES BAO-YEN TSUI.
Fundamentals of global positioning system receivers:a software approach[M].2nd ed. John Wiley & Sons, Inc, 2005: 230-234.
|
| [2] |
王磊. 消除相位翻转影响的扩频信号捕获方法[J]. 中国科学院大学学报, 2015, 32(1):110–115.
|
| [3] |
Parkinson B W, Spilker J J.
Global positioning system:theory and applications Vol[M]. Washington: American Institute of Aeronautics and Astronautics, Inc, 1996: 395-396.
|
| [4] |
Ziedan N I, Garrison J L. Bit synchronization and doppler frequency removal at very low carrier to noise ratio using a combination of the Viterbi algorithm with an extended Kalman filter[C]//Proceedings of the 16th International Technical Meeting of the Satellite Division of the Institute of Navigation. Portland, USA, 2003: 616-627.
https://www.researchgate.net/publication/321254690_Bit_Synchronization_and_Doppler_Frequency_Removal_at_Very_Low_Carrier_to_Noise_Ratio_Using_a_Combination_of_the_Viterbi_Algorithm_with_an_Extended_Kalman_Filter |
| [5] |
Kokkonen M, Pietil S. A new bit synchronization method for a GPS receiver[C]//2002 IEEE Position Location and Navigation Symposium. Palm Springs, CA, USA, 2002: 85-90.
http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=998893 |
| [6] |
Li X, Guo W. Efficient differential coherent accumulation algorithm for weak GPS signal bit synchronization[J]. IEEE Communications Letters, 2013, 17(5):936–939.
DOI:10.1109/LCOMM.2013.031913.130267 |
| [7] |
Kim Y. Holdover clock errors in GPS-disciplined chip-scale atomic clock[C]//Proceedings of the 45th Annual Precise Time and Time Interval Systems and Applications Meeting, Bellevue, Washington, December 2013: 101-106.
http://www.ion.org/publications/abstract.cfm?articleID=11579 |
| [8] |
Mcclelland T, Shtaerman I, Zarjetski E, et al. Disciplined rubidium oscillator for harsh environments[C]//Frequency Control and the European Frequency and Time Forum (FCS), 2011 Joint Conference of the IEEE International, 2011: 1-5.
http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=5977905 |
| [9] |
向为, 徐博, 牟卫华, 等. 基于锁相环的GNSS授时接收机钟差校准算法[J]. 国防科技大学学报, 2013, 35(2):115–119.
|
| [10] |
李志刚, 杨旭海, 施浒立, 等. 转发器式卫星轨道测定新方法[J]. 中国科学:物理力学天文学, 2008, 38(12):1711–1722.
|
| [11] |
杨旭海, 李志刚, 冯初刚, 等. GEO卫星机动后的星历快速恢复方法[J]. 中国科学:物理力学天文学, 2008, 38(12):1759–1765.
|
| [12] |
崔小准, 米红, 李懿, 等. 一种全球定位系统卫星C/A信号通道绝对时延标定算法[J]. 上海交通大学学报, 2012, 46(11):1843–1847.
|
| [13] |
Rovera D, Abgrall M, Uhrich P, et al. Techniques of antenna cable delay measurement for GPS time transfer[C]//Frequency Control Symposium & the European Frequency and Time Forum (FCS), 2015 Joint Conference of the IEEE International, 2015: 239-244.
http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=7138832 |
| [14] |
Kaplan E D, Hegarty C J. GPS原理与应用[M]. 寇艳红, 译. 2版. 北京: 电子工业出版社, 2007.
|
| [15] |
Knight M F. Ionospherie seintillation effects on global positioning system receivers[D]. Adelaide: The University of Adelaide, 2000: 277-281.
|
| [16] |
Aguirre S, Hurd W J. Design and performance of sampled data loops for subcarrier and carrier tracking[J]. Telecommunications & Data Acquisition Progress Report, 1984, 79:81–95.
|
 2018, Vol. 35
2018, Vol. 35 


