随着无线通信技术的发展和4G时代的到来,新一代基于IP的移动宽带网络技术——长期演进技术(long term evolution,LTE)被推出,其共享信道机制[1],即在时域和频域上信道资源被分割成一个个资源块,使得LTE系统下的下行链路的无线资源调度越来越引起人们的关注,目前调度的求解主要根据单信道下的调度算法改进得到。整个无线资源调度过程中,若用户的数据包大小一定,资源块的分配情况主要取决于其传输速率的大小。目前的改进算法多数是资源块传输速率不变的情况下进行的,然而现实生活中无线信道由于受到无线电磁波快慢衰落等因素的影响,在传输用户数据包的过程中具有不确定性,且在不同的时隙不同的资源块传输不同的用户数据包的传输速率也是不同的。本文将考虑在资源块不确定的情况下,如何在给定时间段内为用户分配资源块,满足用户时延、丢包率等方面的体验,并使该段时间内资源块的效率最高。
LTE系统下,现有的无线资源调度算法多数是根据轮询算法(RR)[2]、最大载干比调度算法(MAX C/I)[3]和比例公平调度算法(PF)[4]思想,考虑信道质量,QoS等某一方面或两方面结合的性能指标改进得到的,如半持续调度算法[5]、log-rule算法[6]等。这些算法都是在传输速率确定不变的前提下,对于不确定传输速率的调度算法研究较少,本文将采用鲁棒优化方法求解。鲁棒优化方法是一种新的研究不确定优化问题的方法,适于刻画和求解不确定传输速率下的无线资源调度问题。它的主要思想是首先确立确定性的问题模型,然后根据不确定参数在目标和约束中的位置建立不确定的鲁棒优化模型,最后根据不确定参数集合的性质建立相应的鲁棒对应模型进行求解。在建立不确定鲁棒优化模型时,根据不确定量出现的位置在确定性问题的基础上建立不确定的鲁棒优化模型,若不确定量出现在目标上,选择相应的鲁棒对应准则——绝对鲁棒准则、鲁棒偏离准则和相对鲁棒准则;若出现在约束中,要求不论不确定量如何变化,约束都要满足。一般来说,建立不确定鲁棒优化模型均不易求解,尤其不确定量在约束中时,几乎是不可精确求解的,因此关键是建立确定性的鲁棒对应模型进行求解,找到合理等价的鲁棒对应模型对原不确定性鲁棒优化问题进行转化。在实际不确定传输速率调度问题中,可以首先根据历史信息确定传输速率的变化集合或者变化特性,然后根据确定的不确定集合及对应参数确定相应的鲁棒优化问题,最后利用软件或者其他算法求解,进而得出无论传输速率在不确定集内如何变化都可以满足用户需求的无线资源调度方案。
目前关于鲁棒优化方法的研究有很多,其中理论上和实际应用中涉及鲁棒对应模型的研究有如下:Ben-Tal等[7]研究鲁棒线性优化问题;Kouvelis和Yu[8]研究离散鲁棒优化问题;Delage和Ye[9]将随机规划与鲁棒优化方法结合通过半定规划的鲁棒对应模型求解数据流问题;Li等[10]对鲁棒线性规划和混合整数线性规划问题在特殊的不确定集下的鲁棒对应问题做了详细的研究;Xu等[11]将机会约束与鲁棒优化结合并将原规划模型近似为一个易于求解的半定规划问题;Zymler等[12]研究已知二阶矩信息的分布式棒联合机会约束模型,并利用最坏风险值思想给出该模型的半定规划近似模型;Sun等[13]给出需求不确定的网络流设计问题的分布式鲁棒优化模型,并找到线性规划、半定规划、二阶锥规划的不同近似分别求解等等。
本文在具体描述无线资源调度问题,并给出该问题的确定性线性规划模型的基础上,通过分析不确定传输速率所属的盒子集合、椭球集合及已知部分分布信息集合的特点,利用凸优化对偶理论和概率不等式给出相应的鲁棒对应模型;然后利用具体实例分析验证鲁棒对应模型的有效性并分析不确定集的不同对目标的影响。
1 问题描述无线资源调度是一类特殊的具有参数不确定的组合优化问题,与经典的调度问题有着本质的不同。在无线资源调度问题中,在不同的时刻利用不同的信道为不同的用户发送数据包的传输速率是不确定的,且无法事先准确知道,这就从通信网络的实际应用中提出一类新的不确定无线资源调度问题。为了更加清楚地说明问题,本文对无线资源调度问题作以下假设:
A1)每个用户每隔相同的时间产生一个数据包;
A2)每个用户每次产生的数据包大小相同;
A3)每个用户产生数据包的时间同步;
A4)每个数据包的时延相同;
A5)数据包可以累积并按照先进先出的规则传输;
A6)每个数据包可以拆开传输;
A7)每一时隙一个资源块只能为一个用户服务,但同一时隙可以有多个资源块为一个用户服务。
基于上述假设本文给出该问题的具体描述:
设考虑时间范围为T,T是由t=1, 2, …, T个时隙组成,一个时隙等于1 ms;有N个用户,每个用户每隔ΔT ms产生一个数据包,并且每个数据包的大小相同均为c0。为了方便计算,假设在t=1时每个用户都刚好产生一个数据包;有R个信道资源块(resource block, RB),其传输速率vn, r, t与时隙t、用户n和资源块r均相关,即不同的时隙不同的资源块传输不同用户的数据时传输速率均不相同。现要求给出每个时隙内给每个用户配置资源块的策略xn, r, t,即t时隙是否为用户n配置资源块r为其传输数据,若是,则其值为1;否则为0。同时要求配置结果满足以下条件:
1) 资源块使用效率尽可能高,即资源块使用数量尽可能少;
2) 每个数据包的时延都不超过DL,即每个用户的数据包必须在其产生后的DL时间段内传输完毕。
令用户集合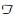
M1(DWRSM):
| $ \min \sum\limits_{t = 1}^T {\sum\limits_{n = 1}^N {\sum\limits_{r = 1}^R {{x_{n, t, r}}} } } $ | (1) |
subject to
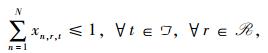
|
(2) |
| $ \sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, t, r}}{v_{n, t, r}}} } \ge {c_0}, \forall I \in \mathscr{T}, \forall n \in \mathscr{N}, $ | (3) |
| $ \sum\limits_{t = 1}^{\left( {i - 1} \right)\mathit{\Delta } t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{v_{n, r, t}}} } \ge i{c_0}, \forall i \in \mathscr{T}, \forall n \in \mathscr{N}, $ | (4) |
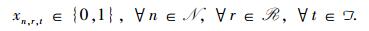
|
(5) |
其中,目标(1)为最小化T时段内资源块使用数量;约束(2)表示每一时隙内一个资源块只能为一个用户服务;约束(3)表示每个用户自产生数据包的时刻开始以后的DL个时隙内被传输的数据量大于1个数据包的大小;约束(4)表示从第1个时隙开始到第i个数据包的时延时隙,每个用户被传输的数据量不小于I个数据包的大小,可以看到这里约束(3)和(4)共同保证用户的每个数据包在时延范围内传输完毕,可以验证只有一个约束是不行的;约束(5)是决策变量xn, r, t的0, 1约束。
M1是0~1整数规划模型,是Karp[14]于1972年提出的21个NPC问题之一,因此无法在多项式时间内找到最优解。目前求解NPC问题的算法有分支定界法、完全枚举法、动态规划法和遗传算法等,其中最常用的是分支定界法,本文也采用该方法利用软件MTLAB求解。
2 无线资源调度的鲁棒优化模型M1是建立在每个资源块的传输速率不变的基础上的,而现实生活中信道质量由于受到电磁波等外界因素的干扰而变化,从而导致资源块的传输速率不是确定不变的。本文将重点研究当传输速率变化时如何为用户分配资源块,并且满足用户在时延、丢包率等方面的要求。对于不确定优化问题的求解,目前应用较多的是随机优化和鲁棒优化,其中前者需要已知确定的概率分布,求得的解也比较特殊,是很早就提出来的一种方法;而后者仅需要不确定量的变化范围,求得最坏情况下的最优解,较为保守,是近20年来研究较热的方法,也在实际问题中得到了有效的应用。本节将利用鲁棒优化的方法对不确定传输速率的无线资源调度问题进行分析并建立鲁棒优化模型,然后分析不确定传输速率的变化集合——盒子不确定集、椭球不确定集和已知部分概率信息的不确定集的特点,分别建立相应的不确定无线资源调度问题的合理等价的鲁棒对应模型。首先,给出不确定传输速率的无线资源调度鲁棒优化模型(uncertain wireless resource scheduling model, UWRSM)。
M2(UWRSM):
| $ \min \sum\limits_{t = 1}^T {\sum\limits_{n = 1}^N {\sum\limits_{r = 1}^R {{x_{n, t, r}}} } } $ |
subject to (2), (5)
| $ \begin{array}{*{20}{c}} {\sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{{\tilde v}_{n, r, t}}} } \ge {c_0}, \forall \tilde v \in V, }\\ {\forall i \in \mathscr{T}, \forall n \in \mathscr{N}, } \end{array} $ | (6) |
| $ \begin{array}{*{20}{c}} {\sum\limits_{t = 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{{\tilde v}_{n, r, t}}} } \ge i{c_0}, \forall \tilde v \in V, }\\ {\forall i \in \mathscr{T}, \forall n \in \mathscr{N}, } \end{array} $ | (7) |
其中,
鲁棒优化方法是处理不确定优化问题的一种新的建模方法,用该方法处理考虑不确定因素的问题时,只需知道不确定量的变化范围,因此利用鲁棒的方法来研究这类不确定调度问题,既有很强的可行性又能反映实际调度问题的不确定特征。利用鲁棒优化求解该问题时,假设不确定量可以被一些主要的不确定因素仿射表示,即对ξn, r, t,有
| $ {{\tilde v}_{n, r, t}} = {v_{n, r, t}} + {\xi _{n, r, t}}, {{\hat v}_{n, r, t}}, \;\;\;\forall {\xi _{n, r, t}} \in U, $ | (8) |
其中:vn, r, t为名义值;
将等式(8)代入不确定模型中,再对不等式约束(6)、(7)进行分析,由于二者的相似性,仅以约束(6)为例具体分析,约束(7)可类似给出,不等式(6)可表示为
| $ \begin{array}{*{20}{c}} {\sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{v_{n, r, t}}} } + \sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{{\hat v}_{n, r, t}}{\xi _{n, r, t}}} } }\\ { \ge {c_0}, \;\;\forall \xi \in U, \;\;\forall i, n, } \end{array} $ | (9) |
| $ \begin{array}{*{20}{c}} {\sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{v_{n, r, t}}} } + }\\ {\mathop {\min }\limits_{\forall \xi \in U} \left( {\sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{{\hat v}_{n, r, t}}{\xi _{n, r, t}}} } } \right) \ge {c_0}, \forall i, n.} \end{array} $ | (10) |
盒子不确定集是由不确定数据向量的∞-范数来描述的,即
| $ U = \left\{ {\xi \left| {{{\left\| \xi \right\|}_\infty } \le \psi } \right.} \right\} = \left\{ {\xi \left| {\left| {{\xi _j}} \right| \le \psi } \right., \forall j} \right\}, $ |
其中,ψ是控制不确定集大小的参数。
引理2.1 当不确定集U={ξ||ξi|≤ψ, ∀i}时,对任意的a=(…, aj, …),有下式成立:
| $ \mathop {\max }\limits_{\forall \xi \in U} \left( {\sum\limits_{j = 1}^n {{a_j}{\xi _j}} } \right) = \psi \sum\limits_{j = 1}^n {\left| {{a_j}} \right|} . $ |
证明 已知U=U∞={ξ||ξj≤ψ, ∀j},
设P∞=[In×n; 01×n], p∞=[0n×1; ψ],
| $ {K_\infty } = \left\{ {\left[{{\theta _{n \times 1}};t} \right] \in {R^{n + 1}}|{{\left\| \theta \right\|}_\infty } \le t} \right\}, $ |
于是最大化问题
| $ \mathop {\max }\limits_\xi \left\{ {\sum\limits_{j = 1}^n {{a_j}{\xi _j}\left| {{P_\infty }\xi + {p_\infty }} \right.} \in {K_\infty }} \right\}. $ |
利用Lagrange对偶求上述优化的对偶问题,设对偶变量为y=[λ; τ]∈Rn×1,K∞的对偶锥为K∞*={[θn×1; t]∈Rn+1|‖θ‖1≤t}, 于是上述最大化问题可以重新表示为
| $ \mathop {\min }\limits_{\lambda, \tau } \left\{ {\psi \tau \left| {{\lambda _j} = {a_j}, \forall j, {{\left\| \lambda \right\|}_1} \le \tau } \right.} \right\}. $ |
由于这是一个最小化问题,该优化问题可以进一步整理为
| $ \mathop {\min }\limits_{\lambda, \tau } \left\{ {\psi \sum\limits_{j = 1}^n {\left| {{\lambda _j}} \right|\left| {{\lambda _j} = {a_j}} \right.}, \forall j} \right\} = \psi \sum\limits_{j = 1}^n {\left| {{a_j}} \right|}, $ |
引理得证。
利用上述引理2.1,可得不等式约束(11)等价于
| $ \begin{array}{*{20}{c}} { - \sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{v_{n, r, t}}} } + \sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {\psi \left| {{x_{n, r, t}}{{\hat v}_{n, r, t}}} \right|} } }\\ { \le - {c_0}, \;\;\forall i, n, } \end{array} $ | (11) |
| $ \begin{array}{*{20}{c}} { - \sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{v_{n, r, t}}} } + \psi \sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{{\hat v}_{n, r, t}}} } }\\ { \le - {c_0}, \;\;\forall i, n.} \end{array} $ | (12) |
因此,不确定集为U={ξ||ξi|≤ψ, ∀i}时,不确定传输速率的无线调度鲁棒模型等价于
M3(UWRSM-LP):
| $ \min \sum\limits_{t = 1}^T {\sum\limits_{n = 1}^N {\sum\limits_{r = 1}^R {{x_{n, t, r}}} } } $ |
subject to (2), (5)
| $ \begin{array}{*{20}{c}} { - \sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{v_{n, r, t}}} } + \psi \sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{{\hat v}_{n, r, t}}} } }\\ { \le - {c_0}, \;\;\forall i, n, } \end{array} $ |
| $ \begin{array}{*{20}{c}} { - \sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{v_{n, r, t}}} } + \psi \sum\limits_{t = 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{{\hat v}_{n, r, t}}} } }\\ { \le - i{c_0}, \;\;\forall i, n.} \end{array} $ |
椭球不确定集是由不确定数据向量的2-范数来描述的,即
| $ U = \left\{ {\xi \left| {{{\left\| \xi \right\|}_2} \le \mathit{\Phi }} \right.} \right\} = \left\{ {\xi \left| {\sqrt {\sum\limits_{j = 1}^n {\xi _j^2} } \le \mathit{\Phi }} \right.} \right\}, $ |
其中,Φ是控制不确定集大小的参数。
引理2.2 当不确定集
| $ \mathop {\max }\limits_{\forall \xi \in U} \left( {\sum\limits_{j = 1}^n {{a_j}{\xi _j}} } \right) = \mathit{\Phi }\sqrt {\sum\limits_{j = 1}^n {a_j^2} } . $ |
证明 可类似引理2.1的证明,利用Lagrange对偶和对偶范数证明得到。
根据引理2.2,原不确定调度模型中的不等式约束(13)等价于
| $ \begin{array}{*{20}{c}} { - \sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{v_{n, r, t}}} } + }\\ {\mathit{\Phi }\sqrt {\sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{{\left( {{x_{n, r, t}}{{\hat v}_{n, r, t}}} \right)}^2}} } } \le - {c_0}, \forall i, n.} \end{array} $ | (13) |
因此,不确定集为
M4(UWRSM-SOCP1):
| $ \min \sum\limits_{t = 1}^T {\sum\limits_{n = 1}^N {\sum\limits_{r = 1}^R {{x_{n, t, r}}} } } $ |
subject to (2), (5)
| $ \begin{array}{*{20}{c}} { - \sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{v_{n, r, t}}} } + }\\ {\mathit{\Phi }\sqrt {\sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{{\left( {{x_{n, r, t}}{{\hat v}_{n, r, t}}} \right)}^2}} } } \le - {c_0}, \forall i, n, } \end{array} $ |
| $ \begin{array}{*{20}{c}} { - \sum\limits_{t = 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{v_{n, r, t}}} } + }\\ {\mathit{\Phi }\sqrt {\sum\limits_{t = 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{{\left( {{x_{n, r, t}}{{\hat v}_{n, r, t}}} \right)}^2}} } } \le - i{c_0}, \forall i, n.} \end{array} $ |
假设已知不确定传输速率的部分概率信息,即均值和方差,考虑利用分布式鲁棒联合机约束的方法求解,该方法结合了随机规划与鲁棒优化的特点。从上述两种不确定鲁棒优化模型可以看出鲁棒优化的方法要求不等式约束对于所有的不确定量都满足,求出的解比较保守;而机会约束对不确定量要求稍微放松一些,它并不要求所有的不确定量都成立,而是需要以较大的概率满足即可,求出的解可能对于部分不确定变量的取值稍微变动就会导致约束不满足,因此本小节考虑鲁棒优化与机会约束相结合的方式求解,即建立无线资源调度的分布式鲁棒联合机会约束模型。
首先给出不确定传输速率无线资源调度问题的机会约束模型
| $ \min \sum\limits_{t = 1}^T {\sum\limits_{n = 1}^N {\sum\limits_{r = 1}^R {{x_{n, t, r}}} } } $ |
subject to (2), (5)
| $ \begin{array}{*{20}{c}} {P\left( {\sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{{\tilde v}_{n, r, t}}} } \ge {c_0}, \forall i \in \left\{ {1, 2, \cdots, I} \right\}, } \right.}\\ {\left. {\forall n \in \left\{ {1, 2, \cdots, N} \right\}} \right) \ge \varepsilon, } \end{array} $ |
| $ \begin{array}{*{20}{c}} {P\left( {\sum\limits_{t = 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{{\tilde v}_{n, r, t}}} } \ge i{c_0}, \forall i \in \left\{ {1, 2, \cdots, I} \right\}, } \right.}\\ {\left. {\forall n \in \left\{ {1, 2, \cdots, N} \right\}} \right) \ge \varepsilon, } \end{array} $ |
其中,
将上述模型结合鲁棒优化的思想,得到不确定传输速率无线资源调度的分布式鲁棒模型如下
| $ \min \sum\limits_{t = 1}^T {\sum\limits_{n = 1}^N {\sum\limits_{r = 1}^R {{x_{n, t, r}}} } } $ |
subject to (2), (5)
| $ \begin{array}{*{20}{c}} {\mathop {{\rm{Inf}}}\limits_{P \in P} P\left( {\sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{{\tilde v}_{n, r, t}}} } \ge {c_0}, } \right.}\\ {\forall i \in \left\{ {1, 2, \cdots, I} \right\}, \left. {\forall n \in \left\{ {1, 2, \cdots, N} \right\}} \right) \ge \varepsilon, } \end{array} $ | (14) |
| $ \begin{array}{*{20}{c}} {\mathop {{\rm{Inf}}}\limits_{P \in P} P\left( {\sum\limits_{t = 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{{\tilde v}_{n, r, t}}} } \ge i{c_0}, } \right.}\\ {\forall i \in \left\{ {1, 2, \cdots, I} \right\}, \left. {\forall n \in \left\{ {1, 2, \cdots, N} \right\}} \right) \ge \varepsilon .} \end{array} $ | (15) |
可以看出这个模型更具有实际意义,但是在计算上几乎是不可处理的,找不到其等价模型,而且约束(14)、(15)很有可能不是凸的。一种处理这种情况的方法是找到该问题的安全可处理近似,即找到一个确定的约束系统
在求解分布式鲁棒联合机会约束近似之前,首先给出已知部分概率信息的不确定传输速率的描述。假设不确定传输速率可以被一个随机变量η仿射表示,即
| $ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} = \left[{\begin{array}{*{20}{c}} {{\rm{Var}}\left( \eta \right) + E\left( \eta \right)}&{E\left( \eta \right)}\\ {E\left( \eta \right)}&1 \end{array}} \right] = \left[{\begin{array}{*{20}{c}} 1&0\\ 0&1 \end{array}} \right]. $ |
接下来以约束(14)为例进行具体的讨论,约束(15)可类似得到,根据以上描述,约束(14)可进一步表示为
| $ \begin{array}{*{20}{c}} {\mathop {{\rm{Inf}}}\limits_{P \in P} P\left( { - \sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{\mu _{n, r, t}}} } - } \right.}\\ {\left. {\sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{\sigma _{n, r, t}}\eta } } \le - {c_0}, \forall i, \forall n} \right) \ge \varepsilon .} \end{array} $ | (16) |
求解联合约束的近似,最常见的方法是利用Bonfferroni不等式将联合机会约束转化成许多个独立机会约束的和,这样就可以利用独立机会约束来近似求解。利用Bonferroni不等式之前,首先将不等式(16)等价转换为
| $ \begin{array}{*{20}{c}} {\mathop {{\rm{Inf}}}\limits_{P \in P} P\left( { - \sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{\mu _{n, r, t}}} } - } \right.}\\ {\left. {\sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{\sigma _{n, r, t}}\eta } } \le - {c_0}, \forall i, \forall n} \right) \ge \varepsilon, }\\ { \Leftrightarrow \mathop {{\rm{Sup}}}\limits_{P \in P} P\left( {\bigcup\limits_{\forall i, n} { - \sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{\mu _{n, r, t}}} } - } } \right.}\\ {\left. {\sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{\sigma _{n, r, t}}\eta } } > - {c_0}} \right) \le 1 - \varepsilon .} \end{array} $ | (17) |
对上式利用Bonferroni不等式得
| $ \begin{array}{*{20}{c}} {P\left( {\bigcup\limits_{\forall i, n} { - \sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{\mu _{n, r, t}}} } - } } \right.}\\ {\left. {\sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{\sigma _{n, r, t}}\eta } } > - {c_0}} \right)}\\ { \le \sum\limits_{\forall i, n} {P\left( { - \sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{\mu _{n, r, t}}} } - } \right.} }\\ {\left. {\sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{\sigma _{n, r, t}}\eta } } > - {c_0}} \right)}\\ { \le 1 - \varepsilon, \forall P \in P.} \end{array} $ | (18) |
为保证上述不等式成立,要求
| $ \begin{array}{*{20}{c}} {\mathop {{\rm{Sup}}}\limits_{P \in P} P\left( { - \sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{\mu _{n, r, t}}} } - } \right.}\\ {\left. {\sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{\sigma _{n, r, t}}\eta } } > - {c_0}} \right) \le {\varepsilon _{i, n}}, } \end{array} $ | (19) |
即
| $ \begin{array}{*{20}{c}} {\mathop {{\rm{Inf}}}\limits_{P \in P} P\left( { - \sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{\mu _{n, r, t}}} } - } \right.}\\ {\left. {\sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{\sigma _{n, r, t}}\eta } } \le - {c_0}} \right) \ge 1 - {\varepsilon _{i, n}}, \forall i, n.} \end{array} $ | (20) |
其中,εi, n为置信水平,并且要求
| $ {\varepsilon _{i, n}} = \frac{{1 - \varepsilon }}{{1 \times N}}, \forall i, n, $ |
其中,I和N分别为用户产生的数据包的个数和用户数,因此
| $ \begin{array}{*{20}{c}} {\mathop {{\rm{Inf}}}\limits_{P \in P} P\left( { - \sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{\mu _{n, r, t}}} } - } \right.}\\ {\left. {\sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{\sigma _{n, r, t}}\eta } } \le - {c_0}} \right) \ge 1 - \frac{{1 - \varepsilon }}{{I \times N}}, \forall i, n.} \end{array} $ | (21) |
根据Calafiore和Ghaoui[16]在关于线性规划的分布式鲁棒优化文章中提出的定理3.1,可得约束(21)可表示为
| $ \begin{array}{*{20}{c}} { - \sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{\mu _{n, r, t}}} } + \sqrt {\frac{{I \times N}}{{1 - \varepsilon }} - 1} }\\ {\sqrt {\sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {x_{n, r, t}^2{\sigma _{n, r, t}}} } } + {c_0} \le 0, \forall i, n.} \end{array} $ | (22) |
对于不等式约束(15)有类似的等价,因此不确定传输速率的分布式鲁棒联合机会约束模型可被近似为如下二次锥规划模型。
M5(UWRSM-SOCP2):
| $ \min \sum\limits_{t = 1}^T {\sum\limits_{n = 1}^N {\sum\limits_{r = 1}^R {{x_{n, t, r}}} } } $ |
subject to (2), (5)
| $ \begin{array}{*{20}{c}} { - \sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{\mu _{n, r, t}}} } + \sqrt {\frac{{I \times N}}{{1 - \varepsilon }} - 1} }\\ {\sqrt {\sum\limits_{t = \left( {i - 1} \right)\Delta t + 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {x_{n, r, t}^2{\sigma _{n, r, t}}} } } + {c_0} \le 0, \forall i, n, } \end{array} $ |
| $ \begin{array}{*{20}{c}} { - \sum\limits_{t = 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{\mu _{n, r, t}}} } + \sqrt {\frac{{I \times N}}{{1 - \varepsilon }} - 1} }\\ {\sqrt {\sum\limits_{t = 1}^{\left( {i - 1} \right)\Delta t + {\rm{DL}}} {\sum\limits_{r = 1}^R {{x_{n, r, t}}{\sigma _{n, r, t}}} } } + i{c_0} \le 0, \forall i, n.} \end{array} $ |
本节通过具体的实例进行上述模型的求解验证,该实例是根据华为公司提供的真实数据提取出来的。考虑T=30 ms时间段内N=5个用户R=2个信道资源块的分配情况,其中每个用户每ΔT=2 ms产生一个大小均为c0的数据包。在实验中我们对c0=100 bit和c0=200 bit均作了分析,这些数据包可以不断累积,假设每个用户产生数据包的时间同步,且第1毫秒每个用户均已经积累了一个数据包;为满足用户的时延要求,每个数据包需要在自它产生的时隙开始DL=10 ms内传输完毕;传输过程中不同的时隙,不同的资源块传输不同的用户的数据包时,传输速率不同。假设实验中不确定的传输速率均以华为公司提供的确定的传输速率为均值,其中最小值是56 bit/ms,最大值是1 608 bit/ms;标准差由MATLAB在0到100之间随机产生,最小值0.19,最大值25.82。在这种情况下考虑如何在30 ms内为用户分配资源块使得资源块利用率最高,即使用的资源块数最少。本文中各种模型均利用软件MATLAB求解,对于整数线性规划利用MATLAB自带线性规划软件包求解,二次锥规划利用MATLAB中的YALMIP工具箱结合SeDuMi求解器进行求解。
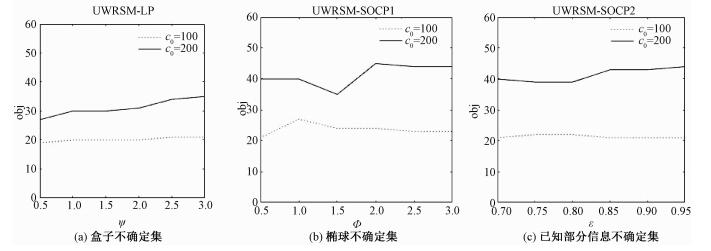
首先,求得传输速率确定时的无线资源调度问题的目标值在c0=100 bit和c0=200 bit时分别为19和26。其次,求出参数变化时3种不同不确定集下鲁棒对应模型的目标值,具体见图 1,从左至右依次为盒子不确定集、椭球不确定集及部分分布信息的不确定集下鲁棒对应模型的目标值与对应参数之间的关系.在图 1中,60为所有模型中目标值的最大值,这可由约束(2)求得。UWRSM-LP和UWRSM-SOCP1的横坐标参数的增大分别表示盒子不确定集和椭球不确定集的增大;UWRSM-SOCP2的横坐标表示约束满足的概率。显然,c0=200 bit时,不确定无线资源调度问题的鲁棒对应模型的最优值均大于确定性模型的最优值,且随着参数的增大,目标值也呈增大趋势,但UWRSM-LP和UWRSM-SOCP2的目标值增长相对稳定。进一步分析,UWRSM-LP的增长幅度大于后二者,且目标值均明显小于后二者。这说明后2种不确定集需要消耗更多的资源块来满足用户的需求。c0=100 bit情况下,传输速率不变,但是需要传输的数据包变为原来的1/2,此时目标值变化不大,且与确定性问题仅相差1,可见约束中的变量对问题影响不大。最后,将这3种鲁棒对应问题求得的资源块分配方案,应用于对应的不确定集中不同的传输速率的确定性无线资源调度模型约束中均得到满足,验证了鲁棒对应模型的可行性。
|
Download:
|
| 图 1 3种不确定集下的鲁棒对应问题目标与参数的关系 Fig. 1 Relationships between objectives and paramatars in the robust problems under three kinds of uncertain sets | |
表 1为c0=200 bit时UWRSM-LP、UWRSM-SOCP1和UWRSM-SOCP2这3种模型在参数变化时的运行时间,可以看出UWRSM-LP运行时间波动较大,十分不稳定;而后二者的运行时间相对稳定,且相差不大,其中UWRSM-SOCP1的运行时间随着不确定集的增大而增大,UWRSM-SOCP2的运行时间随着概率的增大而增大,从模型上看这与UWRSM-SOCP1是一致的,UWRSM-SOCP2中满足约束的概率的增大相当于UWRSM-SOCP1中不确定集的增大。
|
|
表 1 c0=200 bit时3种不确定集下鲁棒对应模型的运行时间 Table 1 Running time of the robust corresponding models under three kinds of uncertain sets when c0=200 bit |
本文利用鲁棒优化方法对不确定传输速率下的无线资源调度问题进行建模求解。根据对确定性无线资源调度问题的建模和分析,可知不确定传输速率仅出现对约束条件有影响,由鲁棒优化的思想,其鲁棒优化模型要求无论不确定传输速率如何变化约束都要满足。这样建立的无线资源调度鲁棒优化模型,几乎是不可求解的,因此要找到其鲁棒对应模型,即用一个确定性的模型与之等价,求解该鲁棒对应模型即可。可见问题的关键在于寻找鲁棒对应模型,而鲁棒对应模型与不确定量所属的集合相关。本文就盒子不确定集、椭球不确定集及仅已知部分分布信息的不确定集3种情况进行具体分析,利用凸优化对偶理论建立前2种情况的鲁棒对应模型,分别为线性规划模型和二次锥规划模型。对于第3种不确定集,根据部分分布信息首先建立机会约束模型,再结合鲁棒优化方法,建立无线资源调度的鲁棒优化联合机会约束模型,最后利用Bonfferroni不等式等概率理论找到它的安全可处理近似为二次锥规划模型。为检验上述鲁棒对应问题的可行性,本文提取华为公司提供的部分真实数据作为实例,利用MATLAB软件包求解,验证了模型的可行性和实用性,随着鲁棒对应问题中参数的变大,对资源块使用的需求也在增加。比较3种不确定集下的模型,盒子不确定集下资源块使用数小于后两者,但随着集合增大目标值增长的幅度较大,求解时间也不稳定。这可能与求解的方法有关,由于本文模型的变量都是0~1的,无多项式时间算法,因此未来考虑利用启发式算法进一步求解这些鲁棒对应问题。不仅如此,在部分分布信息的不确定集下建立的分布式鲁棒优化模型,几乎无法找到其等价的鲁棒对应问题,未来可以考虑更好的安全可处理近似;考虑到无线资源调度问题在实际生活中存在很多不确定的因素,如不确定用户数据包大小,不同时隙在线的用户数等,也可以对其不确定的无线资源调度问题做进一步的研究。
| [1] |
Capozzi F, Piro G, Grieco L A, et al. Downlink packet scheduling in LTE cellular networks:key design issues and a survey[J]. IEEE Communications Surveys & Tutorials, 2012, 15(2):678–700.
|
| [2] |
Kanhere S S, Sethu H, Parekh A B. Fair and efficient packet scheduling using elastic round robin[J]. IEEE Transactions on Parallel & Distributed Systems, 2002, 13(13):324–336.
|
| [3] |
Ericsson N S. Adaptive modulation and scheduling of IP traffic over fading channels[C]//IEEE Vehicular Technology Conference. IEEE, 1999, 2: 849-853.
|
| [4] |
Jalali A, Padovani R, Pankaj R. Data throughput of CDMA-HDR: a high efficiency-high data rate personal communication wireless system[C]//Vehicular Technology Conference Proceedings, 2000. Vtc 2000-Spring Tokyo. 2000 IEEE. IEEE Xplore, 2000, 3: 1854-1858.
http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=851593 |
| [5] |
3GPP. TS36. 321, evolved universal terrestrial radio access, medium access control protocol specification[S]. Sophia Antipolis: ETSI, 2011.
|
| [6] |
Seung B, Gustavo De V, Bilal S. Delay-optimal opportunistic scheduling and approximations:the log rule[J]. IEEE/ACM Transactions on Networking, 2011, 19(2):405–418.
DOI:10.1109/TNET.2010.2068308 |
| [7] |
Ben-Tal A, Ghaoui L E, Nemirovski A.
Robust optimization[M]. Princeton NJ: Princetion University Press, 2009.
|
| [8] |
Kouvelis P, Yu G.
Robust discrete optimization and its applications[M]. Netherlands: Kluwer Academic Publishers, 1997.
|
| [9] |
Delage E, Ye Y. Distributionally robust optimization under moment uncertainty with application to data-driven problems[J]. Operations Research, 2010, 58(3):595–612.
DOI:10.1287/opre.1090.0741 |
| [10] |
Li Z, Ding R, Floudas C A. A comparative theoretical and computational study on robust counterpart optimization:I. Robust linear optimization and robust mixed integer linear optimization[J]. Industrial & Engineering Chemistry Research, 2011, 50(18):10567–10603.
|
| [11] |
Xu H, Caramanis C, Mannor S. Optimization under probabilistic envelope constraints[J]. Operations Research, 2012, 60(3):682–699.
DOI:10.1287/opre.1120.1054 |
| [12] |
Zymler S, Kuhn D, Rustem B. Distributionally robust joint chance constraints with second-order moment information[J]. Mathematical Programming, 2013, 137(1):167–198.
|
| [13] |
Sun H, Gao Z, Szeto W Y, et al. A distributionally robust joint chance constrained optimization model for the dynamic network design problem under demand uncertainty[J]. Networks and Spatial Economics, 2014, 14(3):409–433.
|
| [14] |
Karp R M. Reducibility among combinatorial problems[M]//Miller R E, Thatcher J W, Bohlinger J D(eds). Complexity of Computations. The IBM Research Symposia Series. Boston, MA: Springer, 1972.
|
| [15] |
Nemirovski A, Shapiro A. Convex approximations of chance constrained programs[J]. Siam Journal on Optimization, 2006, 17(4):969–996.
|
| [16] |
Calafiore G C, Ghaoui L E. On distributionally robust chance-constrained linear programs[J]. Journal of Optimization Theory and Applications, 2006, 130(1):1–22.
DOI:10.1007/s10957-006-9084-x |
 2018, Vol. 35
2018, Vol. 35 


