2. 北京工业大学应用数理学院, 北京 100124;
3. 中国科学院大数据挖掘与知识管理重点实验室, 北京 100049
2. College of Applied Sciences, Beijing University of Technology, Beijing 100124, China;
3. Key Laboratory of Big Data Mining and Knowledge Management of Chinese Academy of Sciences, Beijing 100049, China
在经济、医学等众多领域中,由于设备的限制、方法不完善、得到精确的值需要付出很高昂的经济或时间成本,等等原因,经常无法得到精确观测的数据,而是仅仅得到带有测量误差的数据。
当观测数据有测量误差时,若不考虑测量误差,而直接使用带有测量误差的数据进行统计分析,这种方法经常被称为朴素方法(naive method)。使用朴素方法经常会得到不可靠的统计分析结果,比如有偏的估计、效率的损失,检验功效的降低等等。相关的细节可参考文献[1-5]以及这些文献的参考文献。因此有必要对测量误差数据进行专门的处理。
测量误差产生的原因很多,因而种类很多。处理不同测量误差的方法也不一样。本文考虑的测量误差是可加测量误差的一种。我们不假定特别的误差模型结构或已知的误差方差,也不需要重复观测的数据。我们假定真实变量和带有测量误差的变量通过一个工具变量而具有一种非参数结构。这种误差模型结构首先由文献[6]引入,并得到比较深入的研究。详细细节可参见文献[5, 7-10]。
变系数模型,也称为函数系数模型,是一般线性模型的一种有用推广。它既有线性模型易于直观解释的优势,又利于探索数据的动态特征。关于变系数模型的更多细节可以参考文献[11-14]。在本文中,当协变量有测量误差时,在工具变量的帮助下,对变系数测量误差模型的估计问题进行研究。具体处理方法如下:通过工具变量,利用局部常数核方法对测量误差进行校正,从而得到真实观察变量的估计。基于这个估计,采用局部最小二乘法得到系数函数的估计。本文提出的估计方法无需迭代,计算简便。
1 测量误差的校正考虑变系数模型:
| $ Y = \mathit{\boldsymbol{\alpha }}{\left( U \right)^{\rm{T}}}\mathit{\boldsymbol{Z}} + \varepsilon, $ | (1) |
其中Y是一维响应变量,Z、U是协变量,函数型回归系数α(·)=(α1(·), …, αp(·))T。这里T表示向量或矩阵的转置。不失一般性,本文假定U是一维变量。假设模型的误差ε满足E(ε|Z, U)=0,E(ε2|Z, U) < ∞。
可以看到,实际上变系数模型是一个非常一般的模型,许多常用的模型,比如线性模型、可加模型,以及部分线性模型,都可以看作是其特殊情形。
由于测量误差的存在,无法观测到Z的真实值。假设实际中观测到带有测量误差的变量
| $ \mathit{\boldsymbol{Z}} = E\left( {\mathit{\boldsymbol{\tilde Z}}\left| \mathit{\boldsymbol{V}} \right.} \right) = :\mathit{\boldsymbol{\gamma }}\left( \mathit{\boldsymbol{V}} \right), $ | (2) |
其中V是可观测的d维工具变量。此误差模型实际为可加误差的一种特殊情况,因为式(2)等价于
假设得到来自
由式(2),利用局部常数核估计方法可以得到Zi=γ(Vi)的估计:
| $ {{\mathit{\boldsymbol{\hat \gamma }}}_n}\left( {{\mathit{\boldsymbol{V}}_i}} \right) = \sum\limits_{j = 1}^n {{{\mathit{\boldsymbol{\tilde Z}}}_i}{K_v}\left( {{\mathit{\boldsymbol{V}}_i} - {\mathit{\boldsymbol{V}}_j}} \right)} /\sum\limits_{j = 1}^n {{K_v}\left( {{\mathit{\boldsymbol{V}}_i} - {\mathit{\boldsymbol{V}}_j}} \right)} . $ | (3) |
选择多元核函数K(·)为单元二阶核函数的乘积,且式(3)中,
由非参数方法的经典结论可知,
这一节构建系数函数α(u)及其一阶导数的局部线性最小二乘估计。对给定的一点u,可以通过α(Uj), j=1, 2, …, n,在u的一阶线性泰勒展开构建目标局部最小二乘函数如下:
| $ \sum\limits_{j = 1}^n {{{\left[{{Y_j}-\sum\limits_{i = 1}^p {\left\{ {{a_i} + {b_i}\left( {{U_j}-u} \right)} \right\}{Z_{ij}}} } \right]}^2}{\lambda _u}\left( {{U_j} - u} \right)}, $ |
这里λ(u)是核函数,lu是带宽,λu(·)=1/luλ(·/lu)。因为变量Zij未观察到,用其估计
| $ \begin{array}{*{20}{c}} {\mathop {\arg \min }\limits_{\left\{ {{a_i}, {b_i}} \right\}_{i = 1}^p} \sum\limits_{j = 1}^n {\left[{{Y_j}-\sum\limits_{i = 1}^p {\left\{ {{a_i} + {b_i}\left( {{U_j}-u} \right)} \right\} \cdot } } \right.} }\\ {{{\left. {{{\hat \gamma }_{ni}}\left( {{\mathit{\boldsymbol{V}}_j}} \right)} \right]}^2}{\lambda _u}\left( {{U_j} - u} \right).} \end{array} $ | (4) |
注意到目标函数总共有2p个未知参数{ai, bi}i=1p。令
下面给出
| $ {\mathit{\boldsymbol{D}}_u} = \left( {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat \gamma }}}_n}{{\left( {{\mathit{\boldsymbol{V}}_1}} \right)}^{\rm{T}}}}&{{{\mathit{\boldsymbol{\hat \gamma }}}_n}\left( {{\mathit{\boldsymbol{V}}_1}} \right)\left( {{U_1} - u} \right)/{l_u}}\\ {{{\mathit{\boldsymbol{\hat \gamma }}}_n}{{\left( {{\mathit{\boldsymbol{V}}_2}} \right)}^{\rm{T}}}}&{{{\mathit{\boldsymbol{\hat \gamma }}}_n}\left( {{\mathit{\boldsymbol{V}}_2}} \right)\left( {{U_2} - u} \right)/{l_u}}\\ \vdots&\vdots \\ {{{\mathit{\boldsymbol{\hat \gamma }}}_n}{{\left( {{\mathit{\boldsymbol{V}}_n}} \right)}^{\rm{T}}}}&{{{\mathit{\boldsymbol{\hat \gamma }}}_n}\left( {{\mathit{\boldsymbol{V}}_n}} \right)\left( {{U_n} - u} \right)/{l_u}} \end{array}} \right). $ |
这样式(4)可以写成如下形式:
| $ \mathop {\arg \min }\limits_{\left( {\mathit{\boldsymbol{a}}, \mathit{\boldsymbol{b}}} \right)} {\left[{\mathit{\boldsymbol{Y}}-{\mathit{\boldsymbol{D}}_u}\left( {\begin{array}{*{20}{c}} \mathit{\boldsymbol{a}}\\ {{l_u}\mathit{\boldsymbol{b}}} \end{array}} \right)} \right]^{\rm{T}}}{\mathit{\boldsymbol{W}}_u}\left[{\mathit{\boldsymbol{Y}}-{\mathit{\boldsymbol{D}}_u}\left( {\begin{array}{*{20}{c}} \mathit{\boldsymbol{a}}\\ {{l_u}\mathit{\boldsymbol{b}}} \end{array}} \right)} \right], $ |
其中a=(a1(u), a2(u), …, ap(u))T,b=(b1(u), b2(u), …, bp(u))T。令
| $ {{\mathit{\boldsymbol{\hat \theta }}}_n}\left( u \right) = {\left\{ {\mathit{\boldsymbol{D}}_u^{\rm{T}}{\mathit{\boldsymbol{W}}_u}{\mathit{\boldsymbol{D}}_u}} \right\}^{ - 1}}\mathit{\boldsymbol{D}}_u^{\rm{T}}{\mathit{\boldsymbol{W}}_u}\mathit{\boldsymbol{Y}}. $ | (5) |
对于我们感兴趣的系数函数α(u),其估计为
| $ \mathit{\boldsymbol{\hat \alpha }}\left( u \right) = \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_p}}&0 \end{array}} \right){\left\{ {\mathit{\boldsymbol{D}}_u^{\rm{T}}{\mathit{\boldsymbol{W}}_u}{\mathit{\boldsymbol{D}}_u}} \right\}^{ - 1}}\mathit{\boldsymbol{D}}_u^{\rm{T}}{\mathit{\boldsymbol{W}}_u}\mathit{\boldsymbol{Y}}, $ |
其中Ip表示p×1向量,其分量为1。
记
定理2.1 如果条件(C1)~(C5)成立,对固定的某一点u,有下面结论成立:
| $ \begin{array}{l} \sqrt {n~{l_u}} \left\{ {\mathit{\boldsymbol{\hat \alpha }}\left( u \right) - \mathit{\boldsymbol{\alpha }}\left( u \right) - \frac{{{\kappa _{21}}}}{2}{\mathit{\boldsymbol{\alpha }}^{\left( 2 \right)}}\left( u \right)l_u^2} \right\}\\ = {\left( {n~{l_u}} \right)^{ - \frac{1}{2}}}{\mathit{\boldsymbol{Q}}^{ - 1}}\left( u \right)\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{Z}}_i}\lambda \left( {\frac{{{U_i} - u}}{{{l_u}}}} \right){\varepsilon _i}} + \\ \;\;\;{\left( {nh_v^p/{l_u}} \right)^{ - \frac{1}{2}}}{\mathit{\boldsymbol{Q}}^{ - 1}}\left( u \right)\sum\limits_{l = 1}^n {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_u}\left( {{\mathit{\boldsymbol{V}}_l}} \right)\mathit{\boldsymbol{a}}{{\left( u \right)}^{\rm{T}}}\left( {{{\mathit{\boldsymbol{\tilde Z}}}_l} - {\mathit{\boldsymbol{Z}}_l}} \right) + } \\ \;\;\;{o_p}\left( 1 \right). \end{array} $ | (6) |
进一步,有下面结论成立:
| $ \sqrt {nh} \left\{ {\mathit{\boldsymbol{\hat \alpha }}\left( {{u_0}} \right) - \mathit{\boldsymbol{\alpha }}\left( {{u_0}} \right) - \frac{{{\kappa _{21}}}}{2}{\mathit{\boldsymbol{\alpha }}^{\left( 2 \right)}}\left( {{u_0}} \right)l_u^2} \right\}\xrightarrow{d}N\left( {0, {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_u}} \right), $ |
这里
从定理2.1也可以看出,本文所提的基于校正误差的估计是渐近相合的,误差矫正的程序产生的影响体现在(A.25)式的第2项。从定理2.1可以看出,当数据是精确观测的,则有
上面的估计程序实际上给出了函数系数导数的估计,但是因为我们只对系数函数的估计感兴趣,因此不研究其导数函数的渐近性质。仍需要指出的是局部线性方法相比局部常数方法具有多种优势。上面的处理虽然引入讨厌参数,即系数函数的导数,这样的处理是合适的。我们知道局部线性方法得到的估计具有更小的偏差,没有边界效应[20]。直观来看,本文所提的估计应该同样具有这些优点。
非参数方法的一个重要问题是带宽的选择。我们采用一个可行而简便的方案,即结合拇指法则和undersmoothing的需要,在每个方向上按单变量的拇指法则选取带宽,然后用n-1/3取代拇指法则给出的带宽表达式里面的n-1/5。数值模拟结果验证了这样处理的有效性。实际上,选择带宽时,拇指法则充分利用了数据的特点,而对拇指法则选出的带宽进行undersmoothing的操作使得系数函数的估计更为准确。
3 数值模拟本节考虑所提估计的有限样本性质。考虑2个二维变系数模型。
模拟设置Ⅰ:考虑如下模型:
| $ Y = \left( { - U + 0.5} \right){Z_1} + \left( {\exp \left( U \right) - 1.5} \right){Z_2} + \mathit{\boldsymbol{\varepsilon }}, $ |
其中Z1=V2,Z2=2sin(V)+0.5,
模拟设置Ⅱ:考虑下面模型:
| $ Y = 2\sin \left( {{\rm{ \mathsf{ π} }}U} \right){Z_1} + \cos \left( {{\rm{ \mathsf{ π} }}U} \right){Z_2} + \mathit{\boldsymbol{\varepsilon }}, $ |
其中Z1=exp(V)+3cos(πV),Z2=3V+sin(πV),
在上面的2个模型中,模型误差ε均服从均值为0、方差为0.36的正态分布。对每个设置,均考虑两种模型误差:测量误差e均服从均值为0、方差为0.36的正态分布以及均值为0、方差为1的正态分布。
在估计程序中,核函数K(v)和λ(u)均采用Epane-chnikov核函数
对估计量
|
|
表 1 系数函数α1(u)和α2(u)的估计的积分均方误差 Table 1 Mean integrated squared errors (MISE) of the estimators of the coefficient functions α1(u) and α2(u) |
除计算本文提出的基于校正测量误差的系数函数的估计的积分均方误差,还计算了对测量误差无校正,而直接使用带有测量误差的数据进行分析的方法,也即使用naive方法下得到的估计的积分均方误差。作为比较的参考,还计算了当没有测量误差,也即数据是精确观测情况下的系数函数的估计的积分均方误差。详细结果在表 1中列出。从表 1可以看出,本文提出的基于校正误差的估计系数函数的方法相比对模型误差不进行矫正的方法,所得估计具有更小的积分均方误差。相比数据精确观察时的估计方法,本文所提方法略差,具体表现为系数函数的积分均方误差要大一些。因为我们校正误差时引入非参数估计,相比直接使用真实变量的方法,必然会对估计的精确性有影响。这和定理2.1的结果是一致的。我们也发现当样本量增大时,所提方法的均方误差减小,这是合理的。
图 1和图 2分别画出模拟设置Ⅰ和Ⅱ中的2个系数函数的真实曲线、基于本文所提的校正测量误差的估计方法的估计曲线、对测量误差不加以矫正的估计方法的估计曲线以及当不存在测量误差时的估计曲线。2个图体现了相似的变化规律。可以看到,基于精确观察值的估计曲线和本文提出的基于矫正测量误差的估计曲线与真实曲线相差很小,未矫正测量误差的估计曲线与真实曲线有明显偏离。
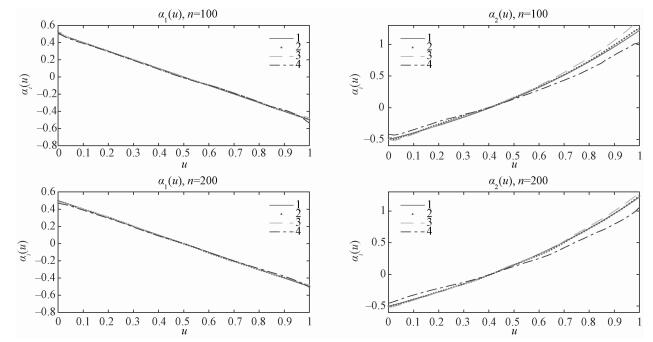
|
Download:
|
| 图例中,实线1:真实曲线;点线2:无测量误差时的估计曲线;虚线3:本文正测量误差的估计曲线;虚线和点线间隔的线4:不对测量误差进行校正的估计曲线。 图 1 模型Ⅰ系数函数α(u)的2个分量函数的真实曲线和估计曲线:测量误差e~N(0, 0.36) Fig. 1 True and estimated curves of the two components of α(u) under model Ⅰ with e~N(0, 0.36) | |

|
Download:
|
| 图例中,实线1:真实曲线;点线2:无测量误差时的估计曲线;虚线3:本文正测量误差的估计曲线;虚线和点线间隔的线4:不对测量误差进行校正的估计曲线。 图 2 模型Ⅱ系数函数α(u)的2个分量函数的真实曲线和估计曲线:测量误差e~N(0, 0.36) Fig. 2 True and estimated curves of the two components of α(u) under model Ⅱ with e~N(0, 0.36) | |
本文考虑协变量有测量误差时变系数模型系数函数的估计。借助工具变量对测量误差进行校正,从而得到真实变量的估计。基于这个估计利用局部线性最小二乘法方法得到系数函数的估计。证明了估计的渐近性质。数值模拟表明所提估计比不进行误差矫正的方法有更好的有限样本性质。
借助工具变量处理测量误差是一种非常有效的方法。今后可以进一步考虑其他半参数测量误差模型基于工具变量的估计方法。也可以进一步考虑其他问题,比如模型检验、模型选择以及变量选择等等问题。
附录:定理2.1的证明
首先给出证明定理所需要的一些条件:
C1:E|ε|2+δ < ∞和E|e|2+δ < ∞对某个δ>0成立;对变量U的定义域支撑内的任一点u,有Q(u)=E(ZZT|U=u)正定;
C2:系数函数α(u),变量U和V的密度函数fu(u)和fv(v)在定义域内点处三阶连续可微;
C3:(ⅰ) K(·)是单元二阶核函数k(·)的乘积;
(ⅱ) λ(·)是单元二阶核函数;
C4:(ⅰ) hv→0, lu→0;
(ⅱ)当n→∞时,n hvd→∞, n lu→∞。
说明:条件(C1)是研究回归模型估计问题经常需要的假定,此条件是为了证明回归系数的渐近正态性。假定条件(C2)~(C4)为应用非参数光滑方法时经常使用的条件。
定理2.1的证明:令
| $ {{\mathit{\boldsymbol{\hat S}}}_n} = \frac{1}{{n~{l_u}}}\sum\limits_{i = 1}^n {\left( {\begin{array}{*{20}{c}} \mathit{\boldsymbol{A}}&{\frac{{\mathit{\boldsymbol{A}}\left( {{U_i} - u} \right)}}{{{l_u}}}}\\ {\frac{{\mathit{\boldsymbol{A}}\left( {{U_i} - u} \right)}}{{{l_u}}}}&{\mathit{\boldsymbol{A}}{{\left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)}^2}} \end{array}} \right)\lambda \left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)} . $ |
由已有的结论
| $ {{\mathit{\boldsymbol{\hat S}}}_n} = \left( {\begin{array}{*{20}{c}} {E\left( {\mathit{\boldsymbol{Z}}{\mathit{\boldsymbol{Z}}^{\rm{T}}}\left| {U = u} \right.} \right)}&0\\ 0&{E\left( {\mathit{\boldsymbol{Z}}{\mathit{\boldsymbol{Z}}^{\rm{T}}}\left| {U = u} \right.} \right){\mu _2}} \end{array}} \right) + {o_p}\left( 1 \right), $ |
其中
| $ \mathit{\boldsymbol{\hat S}}_n^{ - 1} = \left( {\begin{array}{*{20}{c}} \begin{array}{l} {E^{ - 1}}\left( {\mathit{\boldsymbol{Z}}{\mathit{\boldsymbol{Z}}^{\rm{T}}}\left| {U = u} \right.} \right)\\ 0 \end{array}&{\begin{array}{*{20}{c}} 0\\ {\frac{{{E^{ - 1}}\left( {\mathit{\boldsymbol{Z}}{\mathit{\boldsymbol{Z}}^{\rm{T}}}\left| {U = u} \right.} \right)}}{{{\mu _2}}}} \end{array}} \end{array}} \right) + {o_p}\left( 1 \right). $ | (A.1) |
令θ(u)=(a1(u), …, ap(u), lu b1(u), …, lu bp(u))T。由式(5)可以得到
| $ \begin{array}{*{20}{c}} {{{\left( {n~{l_u}} \right)}^{\frac{1}{2}}}\left\{ {{{\mathit{\boldsymbol{\hat \theta }}}_n}\left( u \right) - \mathit{\boldsymbol{\theta }}\left( u \right)} \right\} = {{\left\{ {{{\left( {n~{l_u}} \right)}^{ - \frac{1}{2}}}\mathit{\boldsymbol{D}}_u^{\rm{T}}{\mathit{\boldsymbol{W}}_u}{\mathit{\boldsymbol{D}}_u}} \right\}}^{ - 1}} \times }\\ {\left\{ {{{\left( {n~{l_u}} \right)}^{ - \frac{1}{2}}}\mathit{\boldsymbol{D}}_u^{\rm{T}}{\mathit{\boldsymbol{W}}_u}\left( {\mathit{\boldsymbol{Y}} - {\mathit{\boldsymbol{D}}_u}\mathit{\boldsymbol{\theta }}\left( u \right)} \right)} \right\}.} \end{array} $ | (A.2) |
令
经过简单计算,得到Mn的表达式
| $ \begin{array}{l} {\left( {n~{l_u}} \right)^{ - \frac{1}{2}}}\mathit{\boldsymbol{D}}_u^{\rm{T}}{\mathit{\boldsymbol{W}}_u}\left( {\mathit{\boldsymbol{Y}} - {\mathit{\boldsymbol{D}}_u}\mathit{\boldsymbol{\theta }}\left( u \right)} \right) = :\\ \left\{ \begin{array}{l} {\left( {n~{l_u}} \right)^{ - \frac{1}{2}}}\sum\limits_{i = 1}^n {{{\mathit{\boldsymbol{\hat \gamma }}}_n}\left( {{V_i}} \right)\lambda \left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)\left[{{Y_i}-\sum\limits_{j = 1}^p {\left\{ {{a_j}\left( u \right) + {b_j}\left( u \right)\left( {{U_i}-u} \right)} \right\}{{\hat \gamma }_{nj}}\left( {{\mathit{\boldsymbol{V}}_i}} \right)} } \right]} \\ {\left( {n~{l_u}} \right)^{ - \frac{1}{2}}}\sum\limits_{i = 1}^n {{{\mathit{\boldsymbol{\hat \gamma }}}_n}\left( {{\mathit{\boldsymbol{V}}_i}} \right) \frac{{\left( {{U_i} - u} \right)}}{{{l_u}}}\lambda \left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)\left[{{Y_i}-\sum\limits_{j = 1}^p {\left\{ {{a_j}\left( u \right) + {b_j}\left( u \right)\left( {{U_i}-u} \right)} \right\}{{\hat \gamma }_{nj}}\left( {{\mathit{\boldsymbol{V}}_i}} \right)} } \right].} \end{array} \right. \end{array} $ | (A.3) |
令
| $ {\left( {n~{l_u}} \right)^{\frac{1}{2}}}\left\{ {{{\mathit{\boldsymbol{\hat \alpha }}}_n}\left( u \right) - \mathit{\boldsymbol{\alpha }}\left( u \right)} \right\} = {E^{ - 1}}\left( {\mathit{\boldsymbol{Z}}{\mathit{\boldsymbol{Z}}^{\rm{T}}}\left| {U = u} \right.} \right){\mathit{\boldsymbol{M}}_{n1}} + {o_p}\left( 1 \right). $ | (A.4) |
因此集中关注Mn1。对Mn1, 可以进行如下分解
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_{n1}} = {{\left( {n~{l_u}} \right)}^{ - \frac{1}{2}}}\sum\limits_{i = 1}^n {{{\mathit{\boldsymbol{\hat \gamma }}}_n}{{\left( {{\mathit{\boldsymbol{V}}_i}} \right)}^{\rm{T}}}\lambda \left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)\left[{{Y_i}-\sum\limits_{j = 1}^p {\left\{ {{a_j}\left( u \right) + {b_j}\left( u \right)\left( {{U_i}-u} \right)} \right\}{{\hat \gamma }_{nj}}\left( {{\mathit{\boldsymbol{V}}_i}} \right)} } \right]} = }\\ {{{\left( {n~{l_u}} \right)}^{ - \frac{1}{2}}}\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{Z}}_i}{\lambda }\left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)\left[{{Y_i}-\sum\limits_{j = 1}^p {\left\{ {{a_j}\left( u \right) + {b_j}\left( u \right)\left( {{U_i}-u} \right)} \right\}{{\hat \gamma }_{nj}}\left( {{\mathit{\boldsymbol{V}}_i}} \right)} } \right]} + }\\ {{{\left( {n~{l_u}} \right)}^{ - \frac{1}{2}}}\sum\limits_{i = 1}^n {\left( {{{\mathit{\boldsymbol{\hat \gamma }}}_n}{{\left( {{\mathit{\boldsymbol{V}}_i}} \right)}^{\rm{T}}} - {\mathit{\boldsymbol{Z}}_i}} \right)\lambda \left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)} \times \left[{{Y_i}-\sum\limits_{j = 1}^p {\left\{ {{a_j}\left( u \right) + {b_j}\left( u \right)\left( {{U_i}-u} \right)} \right\}{{\hat \gamma }_{nj}}\left( {{\mathit{\boldsymbol{V}}_i}} \right)} } \right] = }\\ {\mathit{\boldsymbol{M}}_{n1}^{\left[1 \right]} + \mathit{\boldsymbol{M}}_{n1}^{\left[2 \right]}.} \end{array} $ | (A.5) |
对Mn1[1], 有
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{M}}_{n1}^{\left[1 \right]} = {{\left( {n~{l_u}} \right)}^{ - \frac{1}{2}}}\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{Z}}_i}\lambda \left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)} \left( {{Y_i} - \sum\limits_{j = 1}^p {\left\{ {{a_j}\left( u \right) + {b_j}\left( u \right)\left( {{U_i} - u} \right)} \right\}{\mathit{\boldsymbol{Z}}_{ij}}} } \right) + }\\ {{{\left( {n~{l_u}} \right)}^{ - \frac{1}{2}}}\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{Z}}_i}{\lambda }\left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)} \times \sum\limits_{j = 1}^p {\left\{ {{a_j}\left( u \right) + {b_j}\left( u \right)\left( {{U_i} - u} \right)} \right\}\left( {{{\hat \gamma }_{nj}}\left( {{\mathit{\boldsymbol{V}}_i}} \right) - {Z_{ij}}} \right)} = \mathit{\boldsymbol{M}}_{n1, 1}^{\left[1 \right]} + \mathit{\boldsymbol{M}}_{n1, 2}^{\left[2 \right]}.} \end{array} $ | (A.6) |
先考虑Mn1, 1[1]:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{M}}_{n1, 1}^{\left[1 \right]} = {{\left( {n~{l_u}} \right)}^{ - \frac{1}{2}}}\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{Z}}_i}{\lambda }\left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)} \left( {{Y_i} - \sum\limits_{j = 1}^p {{a_j}{U_i}{Z_{ij}}} } \right) + {{\left( {n~{l_u}} \right)}^{ - \frac{1}{2}}}\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{Z}}_i}{\lambda }\left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)} \times }\\ {\sum\limits_{j = 1}^p {\left\{ {{a_j}\left( {{U_i}} \right) - {a_j}\left( u \right) - {b_j}\left( u \right)\left( {{U_i} - u} \right)} \right\}{Z_{ij}}} = {{\left( {n~{l_u}} \right)}^{ - \frac{1}{2}}}\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{Z}}_i}{\lambda }\left( {\frac{{{U_i} - u}}{{{l_u}}}} \right){\varepsilon _i}} + \frac{1}{2}{{\left( {n~{l_u}} \right)}^{ - \frac{1}{2}}} \times }\\ {\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{Z}}_i}{\lambda }\left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)} \sum\limits_{j = 1}^p {a_j^{\left( 2 \right)}\left( u \right){{\left( {{U_i} - u} \right)}^2}{Z_{ij}} + {{\left( {n~{l_u}} \right)}^{ - \frac{1}{2}}}{o_p}\left( {l_u^2} \right)} } \end{array} $ |
可以证明:
| $ \begin{array}{*{20}{l}} {{{\left( {n~{l_u}} \right)}^{ - \frac{1}{2}}}\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{Z}}_i}{\lambda }\left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)} \sum\limits_{j = 1}^p {a_j^{\left( 2 \right)}\left( u \right){{\left( {{U_i} - u} \right)}^2}{Z_{ij}}} }\\ { = {{\left( {n~{l_u}} \right)}^{ - \frac{1}{2}}}\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{Z}}_i}\mathit{\boldsymbol{Z}}_i^{\rm{T}}{a^{\left( 2 \right)}}\left( u \right){{\left( {{U_i} - u} \right)}^2}\lambda \left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)} }\\ { = {{\left( {n~{l_u}} \right)}^{ - \frac{1}{2}}}E\left( {\mathit{\boldsymbol{Z}}{\mathit{\boldsymbol{Z}}^{\rm{T}}}\left| {U = u} \right.} \right){\mathit{\boldsymbol{a}}^{\left( 2 \right)}}\left( u \right){\mu _2}l_u^2 + {o_p}\left( {{{\left( {n~{l_u}} \right)}^{\frac{1}{2}}}} \right)l_u^2.} \end{array} $ |
因此就有
| $ \mathit{\boldsymbol{M}}_{n1, 1}^{\left[1 \right]} = {\left( {n~{l_u}} \right)^{ - \frac{1}{2}}}\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{Z}}_i}{\lambda }\left( {\frac{{{U_i} - u}}{{{l_u}}}} \right){\varepsilon _i}} + {\left( {n~{l_u}} \right)^{ - \frac{1}{2}}}\\\left( {\mathit{\boldsymbol{Z}}{\mathit{\boldsymbol{Z}}^{\rm{T}}}\left| {U = u} \right.} \right){\mathit{\boldsymbol{a}}^{\left( 2 \right)}}\left( u \right){\mu _2}l_u^2 + {o_p}\left( 1 \right). $ | (A.7) |
下面考虑Mn1, 2[1]。根据
| $ \begin{array}{l} \mathit{\boldsymbol{M}}_{n1, 2}^{\left[1 \right]} = {\left( {n~{l_u}} \right)^{ - \frac{1}{2}}}\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{Z}}_i}{\lambda }\left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)} \sum\limits_{j = 1}^p {{a_j}\left( u \right)} \sum\limits_{l = 1}^n {\left( {{{\tilde Z}_{jl}} - {Z_{jl}}} \right)K\left( {\frac{{{\mathit{\boldsymbol{V}}_i} - {\mathit{\boldsymbol{V}}_l}}}{{{h_v}}}} \right)} /\sum\limits_{l = 1}^n {K\left( {\frac{{{\mathit{\boldsymbol{V}}_i} - {\mathit{\boldsymbol{V}}_l}}}{{{h_v}}}} \right)} + \\ ~~~~~{\left( {n~{l_u}} \right)^{ - \frac{1}{2}}}\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{Z}}_i}{\lambda }\left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)} \sum\limits_{j = 1}^p {{b_j}\left( u \right) \times \left( {{U_i} - u} \right)} \sum\limits_{l = 1}^n {\left( {{{\tilde Z}_{jl}} - {Z_{jl}}} \right)K\left( {\frac{{{\mathit{\boldsymbol{V}}_i} - {\mathit{\boldsymbol{V}}_l}}}{{{h_v}}}} \right)} /\sum\limits_{l = 1}^n {K\left( {\frac{{{\mathit{\boldsymbol{V}}_i} - {\mathit{\boldsymbol{V}}_l}}}{{{h_v}}}} \right)} \\ = {\left( {{n^3}~{l_u}~h_v^{2d}} \right)^{ - \frac{1}{2}}}\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{Z}}_i}{\lambda }\left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)} \sum\limits_{j = 1}^p {\frac{{{a_j}\left( u \right)}}{{{f_v}\left( {{V_i}} \right)}}} \times \sum\limits_{l = 1}^n {\left( {{{\tilde Z}_{jl}} - {Z_{jl}}} \right)K\left( {\frac{{{\mathit{\boldsymbol{V}}_i} - {\mathit{\boldsymbol{V}}_l}}}{{{h_v}}}} \right)} + \\ ~~~~~{\left( {{n^3}~{l_u}~h_v^{2d}} \right)^{ - \frac{1}{2}}}\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{Z}}_i}{\lambda }\left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)} \sum\limits_{j = 1}^p {{b_j}\left( u \right) \times \frac{{{U_i} - u}}{{{f_v}\left( {{\mathit{\boldsymbol{V}}_i}} \right)}}} \sum\limits_{l = 1}^n {\left( {{{\tilde Z}_{jl}} - {Z_{jl}}} \right)K\left( {\frac{{{\mathit{\boldsymbol{V}}_i} - {\mathit{\boldsymbol{V}}_l}}}{{{h_v}}}} \right)} + {o_p}\left( 1 \right)\\ = {\left( {{n^3}~{l_u}~h_v^{2d}} \right)^{ - \frac{1}{2}}}\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{Z}}_i}{\lambda }\left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)} \sum\limits_{j = 1}^p {\frac{{{a_j}\left( u \right)}}{{{f_v}\left( {{\mathit{\boldsymbol{V}}_i}} \right)}}} \sum\limits_{l = 1}^n {\left( {{{\tilde Z}_{jl}} - {Z_{jl}}} \right)K\left( {\frac{{{\mathit{\boldsymbol{V}}_i} - {\mathit{\boldsymbol{V}}_l}}}{{{h_v}}}} \right)} + \\ ~~~~~{\left( {{n^3}~{l_u}~h_v^{2d}} \right)^{ - \frac{1}{2}}}\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{Z}}_i}{\lambda }\left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)} \sum\limits_{j = 1}^p {{b_j}\left( u \right) \times \frac{{{U_i} - u}}{{{f_v}\left( {{\mathit{\boldsymbol{V}}_i}} \right)}}} \sum\limits_{l = 1}^n {\left( {{{\tilde Z}_{jl}} - {Z_{jl}}} \right)K\left( {\frac{{{\mathit{\boldsymbol{V}}_i} - {\mathit{\boldsymbol{V}}_l}}}{{{h_v}}}} \right)} + {o_p}\left( 1 \right)\\ = :\mathit{\boldsymbol{M}}_{n1, 21}^{\left[1 \right]} + \mathit{\boldsymbol{M}}_{n1, 22}^{\left[1 \right]} + {o_p}\left( 1 \right). \end{array} $ |
通过简单计算,可证得
| $ \begin{array}{l} \mathit{\boldsymbol{M}}_{n1,2}^{\left[ 1 \right]} = {\left( {{n^3}~{l_u}~h_v^{2d}} \right)^{ - \frac{1}{2}}}\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{Z}}_i}\mathit{\boldsymbol{\lambda }}\left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)} \sum\limits_{j = 1}^p {\frac{{{a_j}\left( u \right)}}{{{f_v}\left( {{\mathit{\boldsymbol{V}}_i}} \right)}}} \times \sum\limits_{l = 1}^n {\left( {{{\tilde Z}_{jl}} - {Z_{jl}}} \right)K\left( {\frac{{{\mathit{\boldsymbol{V}}_i} - {\mathit{\boldsymbol{V}}_l}}}{{{h_v}}}} \right) + {o_p}\left( 1 \right)} \\ = {\left( {n~h_v^{2d}/{l_u}} \right)^{ - \frac{1}{2}}}\sum\limits_{l = 1}^n {\sum\limits_{j = 1}^p {{a_j}\left( u \right)\\\left\{ {\frac{1}{{n~{l_u}}}\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{Z}}_i} \times \mathit{\boldsymbol{\lambda }}\left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)} /{f_v}\left( {{\mathit{\boldsymbol{V}}_i}} \right)K\left( {\frac{{{\mathit{\boldsymbol{V}}_i} - {\mathit{\boldsymbol{V}}_l}}}{{{h_v}}}} \right)} \right\}\left( {{{\tilde Z}_{jl}} - {Z_{jl}}} \right) + {o_p}\left( 1 \right)} } . \end{array} $ |
注意到
| $ {\left( {n~{l_u}} \right)^{ - 1}}\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{Z}}_i}{\lambda }\left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)} /{f_v}\left( {{\mathit{\boldsymbol{V}}_i}} \right)K\left( {\frac{{{\mathit{\boldsymbol{V}}_i} - {\mathit{\boldsymbol{V}}_l}}}{{{h_v}}}} \right) = E\left[{\mathit{\boldsymbol{Z}}/{f_v}\left( \mathit{\boldsymbol{V}} \right)K\left( {\frac{{\mathit{\boldsymbol{V}}-{\mathit{\boldsymbol{V}}_l}}}{{{h_v}}}} \right)\left| {U = u} \right.} \right] + {o_p}\left( 1 \right). $ |
因此有
| $ \begin{array}{l} \mathit{\boldsymbol{M}}_{n1, 2}^{\left[1 \right]} = {\left( {n~h_v^{2d}/{l_u}} \right)^{ - \frac{1}{2}}}\sum\limits_{l = 1}^n {\sum\limits_{j = 1}^p {{a_j}\left( u \right)E\left[{\frac{\mathit{\boldsymbol{Z}}}{{{f_v}\left( \mathit{\boldsymbol{V}} \right)}} \times K\left( {\frac{{\mathit{\boldsymbol{V}}-{\mathit{\boldsymbol{V}}_l}}}{{{h_v}}}} \right)\left| {U = u} \right.} \right]\left( {{{\tilde Z}_{jl}} - {Z_{jl}}} \right) + {o_p}\left( 1 \right)} } \\ \;\;\;\;\;\;\;\; = {\left( {n~h_v^{2d}/{l_u}} \right)^{ - \frac{1}{2}}}\sum\limits_{l = 1}^n {E\left[{\frac{\mathit{\boldsymbol{Z}}}{{{f_v}\left( \mathit{\boldsymbol{V}} \right)}}K\left( {\frac{{\mathit{\boldsymbol{V}}-{\mathit{\boldsymbol{V}}_l}}}{{{h_v}}}} \right)\left| {U = u} \right.} \right] \times \mathit{\boldsymbol{a}}{{\left( u \right)}^{\rm{T}}}\left( {{{\mathit{\boldsymbol{\tilde Z}}}_l} - {\mathit{\boldsymbol{Z}}_l}} \right) + {o_p}\left( 1 \right)} . \end{array} $ |
这个结果结合(A.20)式和(A.25)式,可得
| $ \begin{array}{l} \mathit{\boldsymbol{M}}_{n1}^{\left[1 \right]} = {\left( {n~{l_u}} \right)^{ - 1}}\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{Z}}_i}{\lambda }\left( {\frac{{{U_i} - u}}{{{l_u}}}} \right){\varepsilon _i}} + {\left( {n~{l_u}} \right)^{\frac{1}{2}}}E\left( {\mathit{\boldsymbol{Z}}{\mathit{\boldsymbol{Z}}}\left| {U = u} \right.} \right){\mathit{\boldsymbol{a}}^{\left( 2 \right)}}\left( u \right){\mu _2}~l_u^2 + \\ \;\;\;\;\;\;\;\;\;\;{\left( {\frac{{n~h_v^{2d}}}{{{l_u}}}} \right)^{ - \frac{1}{2}}}\sum\limits_{l = 1}^n {E\left[{\frac{\mathit{\boldsymbol{Z}}}{{{f_v}\left( \mathit{\boldsymbol{V}} \right)}}K\left( {\frac{{\mathit{\boldsymbol{V}}-{\mathit{\boldsymbol{V}}_l}}}{{{h_v}}}} \right)\left| {U = u} \right.} \right] \times \mathit{\boldsymbol{a}}{{\left( u \right)}^{\rm{T}}}\left( {{{\mathit{\boldsymbol{\tilde Z}}}_l} - {\mathit{\boldsymbol{Z}}_l}} \right) + {o_p}\left( 1 \right)} . \end{array} $ | (A.8) |
接下来考虑Mn1[2]:
| $ \begin{array}{l} \mathit{\boldsymbol{M}}_{n1}^{\left[2 \right]} = {\left( {n~{l_u}} \right)^{ - \frac{1}{2}}}\sum\limits_{i = 1}^n {\left( {{{\mathit{\boldsymbol{\hat \gamma }}}_n}{{\left( {{\mathit{\boldsymbol{V}}_i}} \right)}^{\rm{T}}} - {\mathit{\boldsymbol{Z}}_i}} \right)\lambda \left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)} \times \left( {{Y_i} - {\mathit{\boldsymbol{\alpha }}^{\rm{T}}}\left( {{U_i}} \right){\mathit{\boldsymbol{Z}}_i}} \right) + \\ \;\;\;\;\;{\left( {n~{l_u}} \right)^{ - \frac{1}{2}}}\sum\limits_{i = 1}^n {\left( {{{\mathit{\boldsymbol{\hat \gamma }}}_n}{{\left( {{\mathit{\boldsymbol{V}}_i}} \right)}^{\rm{T}}} - {\mathit{\boldsymbol{Z}}_i}} \right)\lambda \left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)} \sum\limits_{j = 1}^p {\left\{ {{a_j}\left( {{U_i}} \right) - \left. {\left\{ {{a_j}\left( u \right) + {b_j}\left( u \right)\left( {{U_i} - u} \right)} \right\}} \right)} \right.{Z_{ji}}} + \\ \;\;\;\;\;{\left( {n~{l_u}} \right)^{ - \frac{1}{2}}}\sum\limits_{i = 1}^n {\left( {{{\mathit{\boldsymbol{\hat \gamma }}}_n}{{\left( {{\mathit{\boldsymbol{V}}_i}} \right)}^{\rm{T}}} - {\mathit{\boldsymbol{Z}}_i}} \right)\lambda \left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)} \sum\limits_{j = 1}^p {\left\{ {{a_j}\left( u \right) + {b_j}\left( u \right)\left( {{U_i} - u} \right)} \right\}\left( {{Z_{ji}} - {{\hat \gamma }_{nj}}\left( {{\mathit{\boldsymbol{V}}_i}} \right)} \right)} \\ \;\;\;\;\; = \mathit{\boldsymbol{M}}_{n1, 1}^{\left[2 \right]} + \mathit{\boldsymbol{M}}_{n1, 2}^{\left[2 \right]} + \mathit{\boldsymbol{M}}_{n1, 3}^{\left[2 \right]}. \end{array} $ |
对Mn1, 1[2], 类似于(A.7)式的推导,可以得到
| $ \mathit{\boldsymbol{M}}_{n1, 1}^{\left[2 \right]} = {\left( {n~{l_u}} \right)^{ - \frac{1}{2}}}\sum\limits_{i = 1}^n {\lambda \left( {\frac{{{U_i} - u}}{{{l_u}}}} \right)\frac{{{Y_i} - {\mathit{\boldsymbol{\alpha }}^{\rm{T}}}\left( {{U_i}} \right){\mathit{\boldsymbol{Z}}_i}}}{{nh_v^d{f_v}\left( {{\mathit{\boldsymbol{V}}_i}} \right)}}} \times \sum\limits_{l = 1}^n {\left( {{{\mathit{\boldsymbol{\tilde Z}}}_l} - {\mathit{\boldsymbol{Z}}_l}} \right)K\left( {\frac{{{\mathit{\boldsymbol{V}}_i} - {\mathit{\boldsymbol{V}}_l}}}{{{h_v}}}} \right)}, $ |
可以证得
| $ \mathit{\boldsymbol{M}}_{n1}^{\left[2 \right]} = {o_p}\left( 1 \right). $ | (A.9) |
由(A.5)式,(A.8)式和(A.9)式,可以得到
| $ \begin{array}{l} {\mathit{\boldsymbol{M}}_{n1}} = {\left( {n~{l_u}} \right)^{ - \frac{1}{2}}}\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{Z}}_i}{\lambda }\left( {\frac{{{U_i} - u}}{{{l_u}}}} \right){\varepsilon _i}} + {\left( {n~{l_u}} \right)^{\frac{1}{2}}}E\left( {\mathit{\boldsymbol{Z}}{\mathit{\boldsymbol{Z}}^{\rm{T}}}\left| {U = u} \right.} \right){\mathit{\boldsymbol{a}}^{\left( 2 \right)}}\left( u \right){\mu _2}~l_u^2 + \\ \;\;\;\;\;\;\;\;\;\;{\left( {\frac{{n~h_v^{2d}}}{{{l_u}}}} \right)^{ - \frac{1}{2}}}\sum\limits_{l = 1}^n {E\left[{\frac{\mathit{\boldsymbol{Z}}}{{{f_v}\left( \mathit{\boldsymbol{V}} \right)}}K\left( {\frac{{V-{V_l}}}{{{h_v}}}} \right)\left| {U = u} \right.} \right] \times \mathit{\boldsymbol{a}}{{\left( u \right)}^{\rm{T}}}\left( {{{\mathit{\boldsymbol{\tilde Z}}}_l} - {\mathit{\boldsymbol{Z}}_l}} \right) + {o_p}\left( 1 \right)} . \end{array} $ |
由条件(C1)和条件(C4)以及中心极限定理,可以证得定理2.1。
| [1] |
Liang H, Hardle W, Carroll R J. Estimation in a semiparametric partially linear errors-in-variables model[J]. Annals of Statistics, 1999, 27(5):1519–1535.
DOI:10.1214/aos/1017939140 |
| [2] |
Roddam A W. Measurement error in nonlinear models:a modern perspective[J]. Journal of the Royal Statistical Society:Series A (Statistics in Society), 2008, 171(2):505–506.
DOI:10.1111/j.1467-985X.2007.00528_4.x |
| [3] |
冯三营, 裴丽芳, 薛留根. 非参数部分带有测量误差的部分线性变系数模型的经验似然推断[J]. 系统科学与数学, 2011, 31(12):1652–1663.
|
| [4] |
Ma Y, Carroll R J. Locally efficient estimators for semiparametric models with measurement error[J]. Journal of the American Statistical Association, 2006, 101(476):1465–1474.
DOI:10.1198/016214506000000519 |
| [5] |
Sun Z, Ye X, Sun L. Consistent test of error-in-variables partially linear model with auxiliary variables[J]. Journal of Multivariate Analysis, 2015, 141(C):118–131.
|
| [6] |
Cai Z, Naik P A, Tsai C L. De-noised least squares estimators:an application to estimating advertising effectiveness[J]. Statistica Sinica, 1970, 10(4):1231–1241.
|
| [7] |
Cui H, He X, Zhu L. On regression estimators with de-noised variables[J]. Statistica Sinica, 2002, 12(4):1191–1205.
|
| [8] |
Li L, Greene T. Varying coefficients model with measurement error[J]. Biometrics, 2008, 64(2):519–526.
DOI:10.1111/j.1541-0420.2007.00921.x |
| [9] |
Zhou Y, Liang H. Statistical inference for semiparametric varying-coefficient partially linear models with error-prone linear covariates[J]. Annals of Statistics, 2009, 37(1):427–458.
DOI:10.1214/07-AOS561 |
| [10] |
Zhao P, Xue L. Variable selection for semiparametric varying coefficient partially linear errors-in-variables models[J]. Journal of Multivariate Analysis, 2010, 101(8):1872–1883.
DOI:10.1016/j.jmva.2010.03.005 |
| [11] |
Hastie T, Tibshirani R. Varying-coefficient models[J]. Journal of the Royal Statistical Society, 1996, 55(4):757–796.
|
| [12] |
Fan J, Zhang W. Simultaneous confidence bands and hypothesis testing in varying-coefficient models[J]. Scandinavian Journal of Statistics, 2000, 27(4):715–731.
DOI:10.1111/sjos.2000.27.issue-4 |
| [13] |
Fan J, Zhang W. Statistical methods with varying coefficient models[J]. Statistics & Its Interface, 2008, 1(1):179–195.
|
| [14] |
Wang L, Li H, Huang J Z. Variable selection in nonparametric varying-coefficient models for analysis of repeated measurements[J]. Journal of the American Statistical Association, 2008, 103(484):1556–1569.
DOI:10.1198/016214508000000788 |
| [15] |
Heckman J J, Urzua S, Vytlacil E. Understanding instrumental variables in models with essential heterogeneity[C]//Review of Economics & Statistics. Geary Institute, University College Dublin, 2006: 389-432.
http://aje.oxfordjournals.org/external-ref?access_num=10.1162/rest.88.3.389&link_type=DOI |
| [16] |
Baum C F, Schaffer M E, Stillman S. Instrumental variables and GMM:estimation and testing[J]. Stata Journal, 2003, 3(1):1–31.
|
| [17] |
Bowden R J, Turkington D A. Instrumental variables[J]. Economic Journal, 1986, 17(3):223–228.
|
| [18] |
Hu Y, Schennach S M. Instrumental variable treatment of nonclassical measurement error models[J]. Econometrica, 2008, 76(1):195–216.
DOI:10.1111/ecta.2008.76.issue-1 |
| [19] |
Buzas J S, Stefanski L A. Instrumental variable estimation in generalized linear measurement error models[J]. Journal of the American Statistical Association, 1996, 91(435):999–1006.
DOI:10.1080/01621459.1996.10476970 |
| [20] |
Fan J, Gijbels I.
Local polynomial modelling and its applications:monographs on statistics and applied probability[M]. London: Chapman & Hall, 1996.
|
| [21] |
Qi L, Racine J S.
Nonparametric econometrics:theory and practice[M]. Princeton: Princeton University press, 2007.
|
| [22] |
Masry Elias. Multivariate local polynomial regression for time series:uniform strong consistency and rates[J]. J Time Ser Anal, 1996, 17:571–599.
DOI:10.1111/j.1467-9892.1996.tb00294.x |
 2018, Vol. 35
2018, Vol. 35 


