2. 中国科学院空间信息处理与应用系统技术重点实验室, 北京 100190;
3. 中国科学院大学, 北京 100049
2. Key Laboratory of Spatial Information Processing and Application System Technology, Chinese Academy of Sciences, Beijing 100190, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
合成孔径雷达(synthetic aperture radar, SAR)是一种具有全天候、全天时对地观测能力的主动式微波成像雷达,并对地表有一定的穿透能力。它通过主动照射地物目标,获取后向散射回波生成高分辨率的二维影像,在资源勘探、军事侦查、灾害与环境监测等方面有重要作用,其中星载合成孔径雷达卫星是以SAR为有效载荷的对地观测卫星[1-3]。与传统单站SAR收发共用不同的是,双站SAR的发射机和接收机分别放置在不同平台上[4],它具有以下优势:1)收发分离,卫星隐蔽能力提高;2)多角度观测地物,信息获取量增加;3)同时观测,地物时间去相干低,大气效应可以互相抵消;4)接收机不含大功率器件,成本低[1, 5]。
然而,双站特有的飞行构型会引入两个技术难点,一是发射机和接收机之间的同步问题,对于同步问题,目前已经有较好的解决方法,如文献[6-7]中提出的空间同步和相位同步方法。还有一个关键问题是双站距离历程的近似问题,对于脉冲体制雷达,单站SAR采用“走停走”假设,其收发距离历程相同,因此其二维频谱具有解析解;但对于双站SAR,收发斜距由于平台的分离不再相等,其距离历程为二者之和,表现为双根号形式,这导致其二维频谱很难求得解析表达式,无法直接沿用单站的成像方法。LBF方法[8-9]和级数反演方法(method of series reversion,MSR)[10]均是基于显式二维频谱的近似求解思路,但需要重新推导成像算法。BP算法[11]可用于各种复杂的成像模式,如移变模式双站SAR,但其计算量较大,无法满足星载SAR成像对实时性的要求。Aria等[12-13]借鉴地震信号处理中的DMO方法,并将该方法应用于双站SAR成像中,其主要思路是对双站SAR回波数据进行预处理转换为单站SAR回波,缺点是只可用于顺飞模式。文献[14]提出一种基线中点单站等效方法,然而其只能适用于基线较短的情况。Bamler等在文献[15-16]中提出两种方法,一种是基于数值计算的NuSAR(numerical SAR)方法,还有一种是双曲等效方法。后一种方法相对于基线中点单站等效方法的精度更高,且能沿用单站SAR的成像算法;但是其三次等效误差会随合成孔径时间的增加而迅速变大,此外随收发平台之间的基线增大其等效误差也会增加。
本文基于单站等效思路,采用Bakhshali近似[17-18]重新计算等效参数,提出一种改进的双曲等效方法,有效地降低了等效误差。同时,基于Bakhshali近似设计了新的CS成像算法流程,提高了成像质量。最后通过计算机仿真进行点目标成像,与改进前的双曲等效方法进行成像结果的对比,仿真结果表明,本文算法提高了星载双站SAR的成像质量。
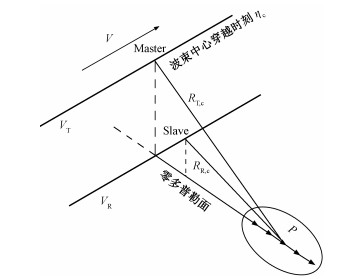
1 双站SAR成像几何模型与信号模型 1.1 双站SAR成像几何模型图 1给出双站SAR成像的几何模型示意图。本文主要研究平飞模式下的双站SAR成像算法并采用正侧视模型进行分析,此外,为保证获取原始数据时方位向的时不变性,假设发射机和接收机的速度近似相等。如图 1所示,VT=VR=V,RT, c和RR, c分别是波束中心穿越时刻ηc发射机和接收机到目标的斜距,在正侧视模型下,波束中心穿越时刻即零多普勒时刻。在任意η时刻,发射机和接收机与目标点P之间的瞬时斜距分别为
| $ \begin{array}{l} {R_{\rm{T}}}\left( \eta \right) = \sqrt {R_{{\rm{T,c}}}^2 + V_{\rm{T}}^2{{\left( {\eta - {\eta _{\rm{c}}}} \right)}^2}} ,\\ {R_{\rm{R}}}\left( \eta \right) = \sqrt {R_{{\rm{R,c}}}^2 + V_{\rm{R}}^2{{\left( {\eta - {\eta _{\rm{c}}}} \right)}^2}} . \end{array} $ | (1) |
|
Download:
|
| 图 1 双站SAR成像几何模型 Fig. 1 Geometry model of bistatic SAR imaging | |
则双站距离历程为
| $ \begin{array}{l} {R_{bi}}\left( \eta \right) = {R_{\rm{T}}}\left( \eta \right) + {R_{\rm{R}}}\left( \eta \right) = \sqrt {R_{{\rm{T,c}}}^2 + V_{\rm{T}}^2{{\left( {\eta - {\eta _{\rm{c}}}} \right)}^2}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\sqrt {R_{{\rm{R,c}}}^2 + V_{\rm{R}}^2{{\left( {\eta - {\eta _{\rm{c}}}} \right)}^2}} . \end{array} $ | (2) |
采用双曲等效方法[19],对Rbi(η)进行单站等效:
| $ {R_{bi}}\left( \eta \right) \approx 2\sqrt {R_{{\rm{m,c}}}^2 + V_{\rm{m}}^2{{\left( {\eta - {\eta _{\rm{c}}}} \right)}^2}} . $ | (3) |
其中,Rm, c表示等效最短斜距,Vm表示等效速度。令η-ηc=ξ,对式(1)和式(3)式泰勒展开到二阶:
| $ \begin{array}{l} {R_{\rm{T}}}\left( \eta \right) = {R_{{\rm{T,c}}}} + \frac{{V_{\rm{T}}^2{\xi ^2}}}{{2{R_{{\rm{T,c}}}}}},\\ {R_{\rm{R}}}\left( \eta \right) = {R_{{\rm{R,c}}}} + \frac{{V_{\rm{R}}^2{\xi ^2}}}{{2{R_{{\rm{R,c}}}}}},\\ {\mathit{R}_{bi}}\left( \eta \right) = 2\left( {{R_{{\rm{m,c}}}} + \frac{{V_{\rm{m}}^2{\xi ^2}}}{{2{R_{{\rm{m,c}}}}}}} \right). \end{array} $ | (4) |
可以求得等效参数:
| $ \begin{array}{l} {R_{{\rm{m,c}}}} = \frac{1}{2}\left( {{R_{{\rm{T,c}}}} + {R_{{\rm{R,c}}}}} \right),\\ V_{\rm{m}}^2 = \frac{1}{2}{R_{{\rm{m,c}}}}\left( {\frac{1}{{{R_{{\rm{T,c}}}}}} + \frac{1}{{{R_{{\rm{R,c}}}}}}} \right){V^2}. \end{array} $ | (5) |
假设发射机发射的信号为线性调频信号,则接收机接收到的回波信号[20-21]为
| $ \begin{array}{*{20}{c}} {s\left( {\tau ,\eta } \right) = {A_p}{w_r}\left( {\tau - \frac{{{R_{bi}}\left( \eta \right)}}{c}} \right){w_{az}}\left( \eta \right) \times }\\ {\exp \left\{ { - {\rm{j}}\frac{{2{\rm{ \mathsf{ π} }}{f_0}{R_{bi}}\left( \eta \right)}}{c} + {\rm{j \mathsf{ π} }}{K_r}{{\left[ {\tau - \frac{{{R_{bi}}\left( \eta \right)}}{c}} \right]}^2}} \right\}.} \end{array} $ | (6) |
式中:τ是距离向时间,η是方位时间,Kr是距离向调频率,Ap为目标的雷达后向散射系数,f0是中心频率,wr(·)是距离向包络,waz(·)是发射和接收天线方向图的综合表示。与单站SAR的信号模型相比,主要的不同之处是距离历程的改变,即收发距离历程为Rbi(η),还有天线方向图的变化。
2 基于Bakhshali近似的改进双曲等效方法对于形如
| $ \sqrt S = \sqrt {{N^2} + d} $ | (7) |
的平方根式,d=S-N2,令
| $ \begin{array}{l} P = \frac{d}{{2N}},\\ A = N + P,\\ \sqrt S \approx A - \frac{{{P^2}}}{{2A}}. \end{array} $ | (8) |
经过上述代数运算,即可得到
| $ \sqrt S = N + \frac{d}{{2N}} - \frac{{{d^2}}}{{8{N^3} + 4Nd}}. $ | (9) |
对于式(7)如果采用泰勒级数展开,保留至二阶,得
| $ \sqrt {{N^2} + d} = N + \frac{d}{{2N}} - \frac{{{d^2}}}{{8{N^3}}}. $ | (10) |
在变量d处展开的泰勒二阶近似与Bakhshali近似的形式非常接近,区别在于二阶项系数中包含变量d。相比于泰勒二阶近似,Bakhshali近似的精度更高。
采用Bakhshali近似计算式(1)、式(3):
| $ \begin{array}{l} {R_{\rm{T}}}\left( \eta \right) = {R_{{\rm{T,c}}}} + \frac{{V_{\rm{T}}^2{\xi ^2}}}{{2{R_{{\rm{T,c}}}}}} - \frac{{V_{\rm{T}}^4{\xi ^4}}}{{8R_{{\rm{T,c}}}^3 + 4{R_{{\rm{T,c}}}}V_{\rm{T}}^2{\xi ^2}}},\\ {R_{\rm{R}}}\left( \eta \right) = {R_{{\rm{R,c}}}} + \frac{{V_{\rm{R}}^2{\xi ^2}}}{{2{R_{{\rm{R,c}}}}}} - \frac{{V_{\rm{R}}^4{\xi ^4}}}{{8R_{{\rm{R,c}}}^3 + 4{R_{{\rm{R,c}}}}V_{\rm{R}}^2{\xi ^2}}},\\ {R_{bi}}\left( \eta \right) = 2\left( {{R_{{\rm{m,c}}}} + \frac{{V_{\rm{m}}^2{\xi ^2}}}{{2{R_{{\rm{m,c}}}}}} - \frac{{V_{\rm{m}}^4{\xi ^4}}}{{8R_{{\rm{m,c}}}^3 + 4{R_{{\rm{m,c}}}}V_{\rm{m}}^2{\xi ^2}}}} \right). \end{array} $ | (11) |
根据式(11)重新计算等效参数,其中Rm, c保持不变,等效速度Vm的计算较为复杂,为了简化运算过程,直接给出结果:
| $ \begin{array}{l} a = 2{R_{{\rm{T,c}}}}{R_{{\rm{R,c}}}}\left[ {4R_{{\rm{T,c}}}^2R_{{\rm{R,c}}}^2 + } \right.\\ \;\;\;\;\;\left. {2{V^2}\left( {R_{{\rm{T,c}}}^2 + R_{{\rm{R,c}}}^2} \right){\xi ^2} + {V^4}{\xi ^4}} \right],\\ b = {V^4}\left( {{R_{{\rm{T,c}}}} + {R_{{\rm{R,c}}}}} \right){\xi ^4} + 8R_{{\rm{T,c}}}^2R_{{\rm{R,c}}}^2\left( {{R_{{\rm{T,c}}}} + {R_{{\rm{R,c}}}}} \right) + \\ 2{V^2}{\xi ^2}\left[ {2{R_{{\rm{T,c}}}}{R_{{\rm{R,c}}}}\left( {{R_{{\rm{T,c}}}} + {R_{{\rm{R,c}}}}} \right) + \left( {R_{{\rm{T,c}}}^3 + R_{{\rm{R,c}}}^3} \right)} \right]. \end{array} $ | (12) |
| $ \begin{array}{l} {P_2} = a{\xi ^2},\\ {P_1} = {R_{{\rm{m,c}}}}\left( {4a{R_{{\rm{m,c}}}} - {V^2}b{\xi ^2}} \right),\\ {P_0} = - 2R_{{\rm{m,c}}}^3{V^2}b \end{array} $ | (13) |
| $ V_{\rm{m}}^2\left( {R;\xi } \right) = \frac{{ - {P_1} + \sqrt {P_1^2 - 4{P_2}{P_0}} }}{{2{P_2}}}. $ | (14) |
需要注意的是,由于等效速度Vm与方位向时间有关,因此不但具有距离空变性,还随方位向时变。为满足后续成像处理对方位向均匀采样的要求,需要重新设计成像算法流程。
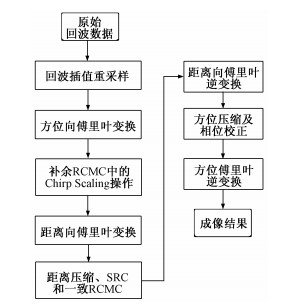
3 改进的CS成像算法流程CS算法是一种频域算法,通过相位相乘实现成像处理,是一种具有良好保相性的成像算法,它兼顾成熟、简单、高效和精确等因素,至今仍是应用最广泛的成像算法,适用于星载SAR成像[1, 22]。采用Bakhshali近似计算的等效速度随方位向变化,所以需要重新设计成像算法流程,图 2是改进后的CS成像算法流程。
|
Download:
|
| 图 2 改进的CS成像算法流程 Fig. 2 Improved procedure of CS imaging algorithm | |
因为采用基于单站等效思路的双曲等效成像方法,成像过程可直接沿用单站SAR的方法,这也是该方法的一大优点。CS算法[23]的关键步骤是三步相位相乘,第一步相位相乘通过变线性标方程实现补余距离徙动校正,使所有目标残余的距离徙动轨迹保持一致,其相位方程为
| $ {\mathit{\Phi }_1} = \exp \left\{ { - {\rm{j \mathsf{ π} }}{K_{r0}}{C_{s0}}\left( {{f_\eta }} \right){{\left[ {\tau - {\tau _{{\rm{ref0}}}}\left( {{f_\eta }} \right)} \right]}^2}} \right\}, $ |
| $ {K_{r0}} = \frac{{{K_r}}}{{1 + {K_r}{R_{{\rm{ref}}}}\frac{{2\lambda }}{{{c^2}}}\frac{{{{\left( {\frac{{\lambda {f_\eta }}}{{2{V_r}}}} \right)}^2}}}{{{{\left[ {1 - {{\left( {\frac{{\lambda {f_\eta }}}{{2{V_r}}}} \right)}^2}} \right]}^{\frac{3}{2}}}}}}}, $ |
| $ \begin{array}{l} {C_{s0}}\left( {{f_\eta }} \right) = \frac{1}{{\sqrt {1 - \left( {\frac{{\lambda {f_\eta }}}{{2{V_r}}}} \right)} }} - 1,\\ {\tau _{{\rm{ref0}}}}\left( {{f_\eta }} \right) = \frac{2}{c}{R_{{\rm{ref}}}}\left[ {1 + {C_{s0}}\left( {{f_\eta }} \right)} \right]. \end{array} $ | (15) |
式中:Rref为参考目标的最短斜距,即Rm, c; 由于距离向和方位向耦合,导致距离向调频率距有所变化,Kr0即为改变后的距离向调频率,具有距离空变性;fη为方位向频率;Cs0(fη)是徙动因子。
第二步相位相乘通过参考函数实现距离压缩,二次距离压缩(SRC)以及一致距离徙动校正,其参考函数为
| $ \begin{array}{*{20}{c}} {{\mathit{\Phi }_2} = \exp \left\{ { - {\rm{j}}\frac{{{\rm{ \mathsf{ π} }}f_\tau ^2}}{{{K_{r0}}\left[ {1 + {C_{s0}}\left( {{f_\eta }} \right)} \right]}}} \right\} \times }\\ {\exp \left\{ {{\rm{j}}\frac{{4{\rm{ \mathsf{ π} }}}}{c}{f_\tau }{R_{{\rm{ref}}}}{C_{s0}}\left( {{f_\eta }} \right)} \right\}.} \end{array} $ | (16) |
最后一步相位相乘通过与随距离变化的匹配滤波器进行相位相乘,实现方位压缩与聚焦,由于第一步相位相乘中的变标操作,这一步中还需要附加一项校正相位[13],其补偿因子为
| $ \begin{array}{*{20}{c}} {{\mathit{\Phi }_3} = \exp \left\{ { - {\rm{j}}\frac{{2{\rm{ \mathsf{ π} }}c\tau }}{\lambda }\left[ {1 - \sqrt {1 - \left( {\frac{{\lambda {f_\eta }}}{{2{V_r}}}} \right)} } \right] + {\rm{j}}\theta \left( {{f_\eta }} \right)} \right\},}\\ {\theta \left( {{f_\eta }} \right) = \frac{{4{\rm{ \mathsf{ π} }}}}{{{c^2}}}{K_{r0}}\left[ {1 + {C_{s0}}\left( {{f_\eta }} \right)} \right]{C_{s0}}\left( {{f_\eta }} \right)\left( {R - {R_{{\rm{ref}}}}} \right).} \end{array} $ | (17) |
式中,R为其他目标点对应的最短斜距。
改进的CS算法与传统CS方法的主要不同之处在于对回波数据的处理。等效速度由于具有时变性,为后续成像处理带来了麻烦,因此需要对其重采样,使回波满足方位向均匀采样的要求。如图 3所示,采用线性插值的方法,以某一距离单元为例,根据已知的相邻两个方位采样点插值出均匀采样点,其线性插值基函数和插值点的计算公式如下:
| $ \begin{array}{l} {l_k}\left( x \right) = \frac{{x - {x_{k + 1}}}}{{{x_k} - {x_{k + 1}}}},\\ {l_{k + 1}}\left( x \right) = \frac{{x - {x_k}}}{{{x_{k + 1}} - {x_k}}}. \end{array} $ | (18) |
| $ {L_1}\left( x \right) = {y_k}{l_k}\left( x \right) + {y_{k + 1}}{l_{k + 1}}\left( x \right). $ | (19) |

|
Download:
|
| 图 3 方位向插值重采样 Fig. 3 Resample by interpolation in azimuth | |
式中: x表示方位向采样点位置信息,y表示回波信息,需要对回波数据的实部和虚部均进行插值。此外,等效速度还具有距离空变性,因此需要对每一距离单元都进行方位向的线性插值重采样。
4 仿真结果与分析本节针对星载双站SAR进行仿真实验,并通过仿真验证本文中提出方法的有效性。本文采用平飞正侧视模型,其成像几何示意图如图 1所示,成像模式为条带模式。星载双站SAR由主星和辅星构成,星历参数如表 1所示,其中主星半长轴为6 795.35 km和6 805.35 km时,对应主辅星间基线距分别0.51 km和10.5 km。仿真卫星采用X波段的中心频率,距离向和方位向的天线尺寸均设为5 m左右,方位向分辨率约为2.5 m,主辅星的成像参数基本相同,具体的成像仿真参数见表 2。
|
|
表 1 主辅卫星星历仿真实验参数 Table 1 Ephemeris simulation parameters of master and slave satellites |
|
|
表 2 主辅卫星成像仿真实验参数 Table 2 Imaging simulation parameters of master and slave satellites |
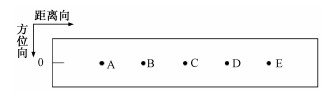
多点目标的分布如图 4所示,沿距离向设置5个点目标,其坐标分别为A(188, 0)、B(262, 0)、C(336, 0)、D(410, 0)、(484, 0),距离向分辨率为0.983 8 m。
|
Download:
|
| 图 4 距离向多点目标分布示意图 Fig. 4 Distribution of multiple targets in range | |
首先分析比较泰勒展开近似与Bakhshali近似的近似精度,对于双站SAR的双根式距离历程,分别采用泰勒二阶、四阶、六阶近似和Bakhshali近似对其展开,以表 3的一组星载仿真参数比较2种方法的近似误差,仿真结果如图 5所示。
|
|
表 3 近似精度比较仿真参数 Table 3 Simulation parameters for comparison of approximation precision |

|
Download:
|
| 图 5 泰勒二阶、四阶以及六阶近似与Bakhshali近似误差对比 Fig. 5 Approximation error comparison between Bakhshali and the second-order, fourth-order, and sixth-order Taylor | |
从图 5可知,对于双根式距离历程,当合成孔径时间较短时,泰勒二阶、四阶以及六阶的近似精度和Bakhshali近似的误差都非常小,接近0,但是当合成孔径时间变长,如图所示超过2 s时,泰勒二阶近似与真实的双根式距离历程的误差迅速增大,而Bakhshali近似在整个仿真所给出的近6 s的合成孔径时间内均非常小。由此可知,对于星载SAR成像几何模型,当合成孔径时间较长时采用Bakhshali近似的距离模型精度更高。
改进前的双曲等效方法采用泰勒二阶近似计算等效斜距和等效速度,改进后的双曲等效方法采用Bakhshali近似计算等效参数,图 6(a)比较2种方法单站等效后的单根式距离历程与真实的双根式距离历程的近似误差,可以看到根据表 3给出的仿真参数,随着合成孔径时间的增加,基于Bakhshali近似的精度相对于泰勒二阶展开整体上提高近2倍,以-3 s时刻为例,改进后的等效误差为9.843e-06 m。

|
Download:
|
| 图 6 两种近似的单站等效误差 Fig. 6 Monostatic equivalence error comparison between two methods | |
为了更好地比较两种双曲等效方法的近似误差,再从双星间基线距变化的角度进行分析,通过收发斜距差来体现,其中发射距离为700 km,接收斜距R1的变化范围为700~1 700 km,方位向时刻固定为-3 s。如图 6(b)所示,可以看到随着收发斜距差的增大,Bakhshali近似误差变化趋势更平缓。图 7对误差随合成孔径时间和收发斜距差的二维变化进行比较,改进后的双曲等效方法整体近似精度有了提高。

|
Download:
|
| 图 7 两种方法的二维误差 Fig. 7 Two-dimensional errors of two methods | |
最后根据表 1和表 2所给的仿真参数以及按图 4设置的多点目标,采用CS算法在未加窗的情况下得到两种双曲等效方法参考目标的聚焦图像和质量参数。
图 8和图 9分别表示主星和辅星间的基线在0.51 km和10.5 km情况下,经典双曲等效方法[15]和本文方法的距离向测绘带多点目标的成像结果,其中等高线图和方位向压缩波形图表示的是景中心C点的成像结果,表 4和表 5列出两种情况下所有点目标距离向和方位向的峰值旁瓣比和积分旁瓣比的结果。

|
Download:
|
| 图 8 基线距为0.51 km时的多点目标成像结果 Fig. 8 Imaging results of multiple targets with the baseline of 0.51 km | |
|
Download:
|
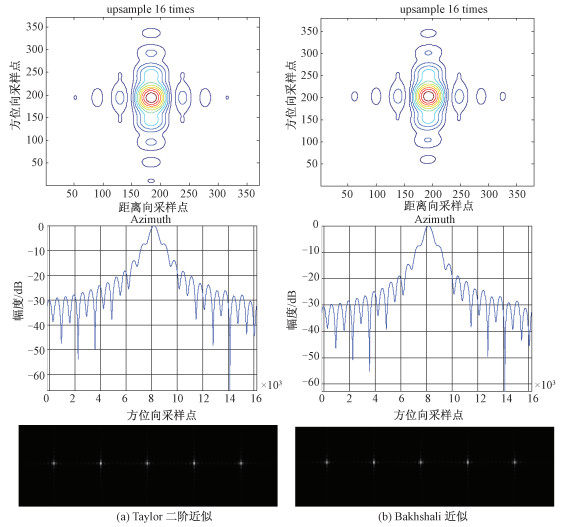
| 图 9 基线距为10.5 km时的多点目标成像结果 Fig. 9 Imaging results of multiple targets with the baseline of 10.5 km | |
|
|
表 4 基线距为0.51 km时两种方法的成像结果 Table 4 Imaging results with the baseline of 0.51 km |
|
|
表 5 基线距为10.5 km时两种方法的成像结果 Table 5 Imaging results with the baseline of 10.5 km |
当基线距为0.51 km时,主辅星间距离较近,相较于经典的双曲等效方法,即采用泰勒二阶近似的方法,本文方法的成像结果质量有轻微的提高。但是当基线距增大到10.5 km时,两种方法方位向都开始散焦,但基于Bakhshali近似的双曲等效方法,其沿距离向多点目标成像结果的峰值旁瓣比和积分旁瓣比均比泰勒二阶近似要好,且有了较为明显的提高,随着基线距的增大,提升效果将会更显著。
5 总结本文基于单站等效思路,提出一种新的基于Bakhshali近似的双曲等效方法,并重新设计适用于新方法的CS成像流程。相比于传统的基于泰勒二阶近似的双曲等效方法,采用Bakhshali近似的双曲等效方法对于双根式距离历程的近似精度更高,误差更低。本文最后通过星载双站SAR的仿真参数对两种等效方法进行误差对比和多点目标仿真,并分别对不同基线距下的成像结果进行指标分析,通过仿真验证了在基线增大和合成孔径时间增加的情况下本文方法的有效性。
| [1] | 魏钟铨. 合成孔径雷达卫星[M]. 北京: 科学出版社, 2001: 1-8. |
| [2] | 黄丽佳, 仇晓兰, 胡东辉, 等. 机载双站聚束SAR改进ωK算法[J]. 电子与信息学报, 2013, 35(9):2154–2160. |
| [3] | 胡继伟, 洪峻. 基于三维重建的分布式卫星SAR干涉测高模型及误差分析[J]. 中国科学院大学学报, 2011, 28(4):489–497. |
| [4] | 陈立福, 林月冠, 彭曙蓉, 等. 一种用于机载双天线InSAR系统的实时DEM生成方法及实现[J]. 中国科学院大学学报, 2014, 31(5):678–684. |
| [5] | 仇晓兰, 丁赤飚, 胡东辉. 双站SAR成像处理技术[M]. 北京: 科学出版社, 2010: 8-9. |
| [6] | 刘建平, 梁甸农. 主星带伴随分布式小卫星雷达系统的波束同步分析[J]. 国防科技大学学报, 2006, 28(2):54–58. |
| [7] | Younis M, Metzig R, Krieger G. Performance prediction of a phase synchronization link for bistatic SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2006, 3(3):429–433. DOI:10.1109/LGRS.2006.874163 |
| [8] | Loffeld O, Nies H, Peters V, et al. Models and useful relations for bistatic SAR processing[J]. IEEE Transanctions on Geoscience and Remote Sensing, 2004, 42(10):2031–2038. DOI:10.1109/TGRS.2004.835295 |
| [9] | Natroshvili K, Loffeld O, Nies H, et al. Focusing of general bistatic SAR configuration data with 2-D inverse scaled FFT[J]. IEEE Transanctions on Geoscience and Remote Sensing, 2006, 44(10):2718–2727. DOI:10.1109/TGRS.2006.872725 |
| [10] | Neo Y L, Wong F, Cumming I G. A two-dimensional spectrum for bistatic SAR processing using series reversion[J]. IEEE Geoscience and Remote Sensing Letters, 2007, 4(1):93–96. DOI:10.1109/LGRS.2006.885862 |
| [11] | 李冉, 皮亦鸣, 张晓玲. 基于改进Bp算法的机载双基地Sar成像[J]. 雷达科学与技术, 2006, 4(6):348–352. |
| [12] | Aria D, Guarnieri A M, Rocca F. Focusing bistatic synthetic aperture radar using dip move out[J]. IEEE Transanctions on Geoscience and Remote Sensing, 2004, 42(7):1362–1376. DOI:10.1109/TGRS.2004.830166 |
| [13] | Ding J, Zhang Z, Xing M, et al. A new look at the bistatic-to-monostatic conversion for Tandem SAR image formation[J]. IEEE Geoscience and Remote Sensing Letters, 2008, 5(3):392–395. DOI:10.1109/LGRS.2008.916645 |
| [14] | 闫鸿慧, 王岩飞, 于海锋, 等. 一种基于距离补偿的分布式小卫星双基Sar成像方法[J]. 电子与信息学报, 2005, 27(5):771–774. |
| [15] | Bamler R, Meyer F, Liebhart W. Processing of bistatic SAR data from quasi-stationary configuration[J]. IEEE Transan-ctions on Geoscience and Remote Sensing, 2007, 45(11):3350–3358. DOI:10.1109/TGRS.2007.895436 |
| [16] | Bamler R, Boerner E. On the use of numerically computed transfer functions for processing of data from bistatic SARs and high squint orbital SARs//International Geoscience and Remote Sensing Symposium, 2005, 86(86):1051-1055. |
| [17] | Channabasappa M N. On the square root formula in the Bakhshali manuscript[J]. Indian Journal of History of Science Calcutta, 1976, 11:112–124. |
| [18] | Duersch M I. Backprojection for Synthetic Aperture Radar. Provo:Brigham Young University, 2013. http://search.proquest.com/docview/1427363335 |
| [19] | Qiu X L, Hu D H, Ding C B. Focusing bistatic images use RDA based on hyperbolic approximating//International Conference on Radar. Shanghai, 2006:1323-1326. |
| [20] | Clemente C, Soraghan J J. Approximation of the bistatic slant range using Chebyshev polynomials[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(4):682–686. DOI:10.1109/LGRS.2011.2178812 |
| [21] | 田卫明, 曾涛, 胡程. 基于导航信号的BiSAR成像技术[J]. 雷达学报, 2013, 2(1):39–45. |
| [22] | Cumming I G, Wong F. 合成孔径雷达成像: 算法与实现[M]. 洪文, 胡光辉, 译. 北京: 电子工业出版社, 2012: 192-193. http://www.bookask.com/book/1791856.html |
| [23] | 张升康, 杨汝良. 双基地合成孔径雷达扩展Chirp Scaling成像算法[J]. 中国科学院大学学报, 2008, 25(1):101–109. |
 2017, Vol. 34
2017, Vol. 34 


