2. 中国科学院空间信息处理与应用系统技术重点实验室, 北京 100190;
3. 中国科学院大学, 北京 100049
2. Key Laboratory of Spatial Information Processing and Application System Technology, Chinese Academy of Sciences, Beijing 100190, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
永久散射体干涉合成孔径雷达(permanent scatterer InSAR,PS-InSAR)技术是利用观测同一地区的多景SAR影像复数据,识别在时间序列上表现出稳定后向散射特性的目标点,进行相干处理,以研究目标在较长时间序列上形变规律的一门技术。相比传统InSAR技术,PS-InSAR能够有效利用已有影像,有效克服时间、空间去相干以及去除大气延迟带来的影响,从而获得毫米级精度的地表形变信息[1-3]。PS-InSAR技术观测范围大,监测点空间密度高,在微小地表形变监测方面具有无与伦比的优势,为地面沉降的预防和治理提供重要的基础数据。
PS-InSAR技术可以获取SAR影像拍摄期间的地表平均形变率以及影像对应时刻的形变量,但是无法预测未来的形变趋势。在很多情况下,仅掌握监测区域的历史形变信息是远远不够的,预测形变量在未来时刻的量值,结合建筑、桥梁、大坝等设计安全预警值,给相关人员提供预警信息,提示管理者对潜在的形变异常位置或者建筑进行安全检查,可有效减少灾难发生和财产损失。目前已有很多理论和方法应用于形变预测,如回归分析方法、时间序列分析方法、灰色模型分析方法、人工神经网络方法等[4-5]。针对桥梁[6]、边坡[5]、隧道[7]等不同地面目标的形变预测研究也在不断深入。这些方法极大地提高了形变预测的精度和可靠性,但是它们大多是预测少量观测点的变化,寻求具有大覆盖范围和高空间分辨率能力的形变预测方法仍是目前需要解决的问题。
针对这些问题,本文将卡尔曼滤波理论与PS-InSAR技术相结合,提出一种新的形变预测方法。首先概述PS-InSAR方法的技术流程,然后根据差分干涉相位模型,从理论上详细推导设计卡尔曼滤波器,最后利用2009—2012年覆盖美国新奥尔良地区的42景TerraSAR数据、2013—2016年覆盖北京通州的32景TerraSAR数据和水准测量数据,验证该方法的有效性。实验结果表明,该算法可以充分利用历史形变数据,发挥PS-InSAR技术通过多景SAR影像统计分析抗时间、空间去相关、减弱大气扰动影响的优点,有效预测每一个PS点的形变趋势,具有较高的空间分辨率、预测精度。
1 PS-InSAR技术流程设研究区有N+1幅不同时间的SAR影像,通过幅度离差法选择出M个PS点。选取其中一幅影像为公共主影像,其余N幅影像为辅影像,分别与主影像进行配准,重采样到同一几何坐标下。辅影像分别与主影像进行相干处理得到N个干涉对,借助已有的数字高程模型(DEM)去除地形相位,就可得到N幅差分干涉图,从而得到各PS点的时间序列差分干涉相位[8]。某一PS点的差分干涉相位为[9]
| $ \begin{array}{l} \phi \left( {X,{t_k}} \right) = {\phi _{{\rm{topo}}}}\left( {X,{b_k}} \right) + {\phi _{{\rm{defo}}}}\left( {X,{t_k}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\phi _{{\rm{atmo}}}}\left( {X,{t_k}} \right) + {\phi _{{\rm{nose}}}}\left( {X,{t_k}} \right),\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;k = 1 \cdots N. \end{array} $ | (1) |
式中:X表示目标在图像中的位置,bk表示空间基线,tk表示与主图像之间的时间间隔,ϕtopo表示DEM误差对应的相位,ϕdefo表示目标形变相位,ϕatmo表示大气相位,ϕnose表示失相关噪声及其他噪声相位。
目标形变一般都是非线性的,所以形变相位ϕdefo(X, tk)可以分为两项
| $ {\phi _{{\rm{defo}}}}\left( {X,{t_k}} \right) = \frac{{4{\rm{ \mathsf{ π} }}}}{\lambda }v\left( X \right) \cdot {t_k} + \frac{{4{\rm{ \mathsf{ π} }}}}{\lambda }{\mu _{{\rm{NL}}}}\left( {X,{t_k}} \right). $ | (2) |
式中:λ表示雷达波长,v(X)表示目标的平均线性形变速率,μNL表示非线性形变分量。因此将差分干涉相位重写为如下形式
| $ \phi \left( {X,{t_k}} \right) = {C_\varepsilon }\left( X \right) \cdot {b_k} + {C_v}\left( X \right) \cdot {t_k} + \omega \left( {X,{t_k}} \right). $ | (3) |
其中
| $ {C_\varepsilon }\left( X \right) = - \frac{{4{\rm{ \mathsf{ π} }}}}{\lambda }\frac{{h\left( X \right)}}{{r\sin \theta }}, $ |
| $ {C_v}\left( X \right) = - \frac{{4{\rm{ \mathsf{ π} }}}}{\lambda }v\left( X \right). $ |
式中: h(X)表示高程误差,r表示主图像中对应的斜距,θ表示入射角,ω(X, tk)中包含大气相位、轨道误差引入的相位、非线性形变相位及热噪声。
接下来对所探测出的PS点构造网络,常用的网络有Delaunay三角网和PS自由网,通过邻近PS点的相位差分可以部分抵消大气相位、轨道误差以及其他系统偏差的影响,在PS点数据集上可以得到较好的形变探测结果[10]。双差分干涉相位可以表示为
| $ \begin{array}{*{20}{c}} {\Delta \phi \left( {{X_r},{X_s},{t_k}} \right) = \phi \left( {{X_r},{t_k}} \right) - \phi \left( {{X_s},{t_k}} \right)}\\ { = \Delta {C_\varepsilon } \cdot {b_k} + \Delta {C_v} \cdot {t_k} + \Delta {\omega _k}.} \end{array} $ | (4) |
根据Ferretti等[9]提出的干涉相关系数最大化思想,求得使下式取得最大值的ΔCε,ΔCv
| $ \gamma = \left| {\frac{{\sum\limits_{k = 1}^N {{{\rm{e}}^{{\rm{j}}\Delta {\omega _k}}}} }}{N}} \right|, $ | (5) |
进而可得每一点的Δv,Δh,采用加权的最小二乘网络平差法计算每一PS点的v,h,ω(X, tk)。为保证最终结果,可以设定一定的门限γ0,剔除γ < γ0的点。对ω(X, tk)在时间上求平均得ω(X),以此作为主图像在点X处大气相位的估计值,而对[ω(X, tk)-ω(X)]时间维的低通滤波获得形变的非线性分量。充分考虑大气相位在时间域呈高频、在空间域呈低频的特点,将大气延迟相位从残余相位中分离出来。大气相位的估计值为
| $ \begin{array}{l} {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \phi } }_{{\rm{atmo}}}}\left( {X,{t_k}} \right) = {\left[ {{{\left[ {\omega \left( {X,t} \right)} \right]}_{{\rm{HP}}\_{\rm{T}}}}} \right]_{{\rm{LP\_Space}}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left[ {\bar \omega \left( X \right)} \right]_{{\rm{LP\_Space}}}}. \end{array} $ | (6) |
为进一步提高形变监测精度,可通过插值获得每幅图像每一点处的大气相位,从差分干涉图中去除大气相位,重新选择PS点,按照上述方法重新估计DEM误差、线性形变率和非线性形变量。
2 卡尔曼滤波器设计卡尔曼滤波是一种线性最小方差滤波方法,通过状态空间法描述系统,能够估计非平稳的矢量信号随机过程,由状态方程和观测方程组成[11]。
经典卡尔曼滤波只能解决线性系统状态估计问题,此处为非线性问题,故采用线性近似方式,用线性化方法处理非线性系统的估计。卡尔曼滤波是当前应用最广的一种动态数据处理方法,具有最小无偏差性,它的最大特点是能够剔除随机干扰误差,从而获取逼近真实情况的有用信息[12]。它不但可以用于数据的检验, 还可以用于数据的预测预报。在测量界在应用中对卡尔曼滤波进行了多方面研究,尤其在变形监测方面其应用最为广泛。卡尔曼滤波可以根据前一个时刻形变量的最优估计值与最近一个实测形变值,估计的当前形变量,通过其状态方程、观测方程及更新过程进行估计,结果是估计值。在动态形变监测的工作中,运用扩展卡尔曼滤波技术进行滤波及预报具有重要意义。
在详细推导状态方程和观测方程之前,作如下说明:假设已经利用PS-InSAR技术完成对历史影像的处理,且处理结果精度足够理想,校正后DEM、线性形变率和形变量等处理结果作为后续滤波器设计的基础;PS点提取、主图像选取、参考点选择等工作不再重复进行;预测形变量仍然相对参考点的相对值,而非绝对值。
2.1 状态方程利用PS-InSAR形变监测技术仅可获取图像对应时刻的形变量,形变一般为非线性的,为了近似得到形变量随时间变化的解析形式,可以通过离散时刻的形变量拟合出每一PS点的形变量函数。由于PS-InSAR技术获得是相对于主图像获取时刻的形变量,所以拟合出的形变量函数也是相对于主图像获取时刻的变化情况。拟合采用的基函数可以是多项式函数、三角函数等,多项式次数或者基函数类型可以根据实际情况选择,本文采用的是三次多项式进行拟合
| $ \begin{array}{*{20}{c}} {{\mu _i}\left( t \right) = {a_i} + {b_i}t + {c_i}{t^2} + {d_i}{t^3},}\\ {i = 1 \cdots M.} \end{array} $ | (7) |
式中: t表示相对于主图像的时间间隔,ai、bi、ci、di为多项式系数。对式(7)离散化,相邻两图像获取时刻的形变量表达式为
| $ \begin{array}{l} \mu _k^i = {a_i} + {b_i}\left( {{t_{k - 1}} + T} \right) + {c_i}{\left( {{t_{k - 1}} + T} \right)^2} + \\ \;\;\;\;\;\;\;{d_i}{\left( {{t_{k - 1}} + T} \right)^3},\\ \mu _{k - 1}^i = {a_i} + {b_i}{t_{k - 1}} + {c_i}t_{k - 1}^2 + {d_i}t_{k - 1}^3. \end{array} $ | (8) |
上式两项相减并移项,可得两个时刻形变量关系式
| $ \begin{array}{l} \mu _k^i = \mu _{k - 1}^i + {b_i}T + {c_i}\left[ {{{\left( {{t_{k - 1}} + T} \right)}^2} - t_{k - 1}^2} \right] + \\ \;\;\;\;\;\;\;\;{d_i}\left[ {{{\left( {{t_{k - 1}} + T} \right)}^3} - t_{k - 1}^3} \right]. \end{array} $ | (9) |
式中T表示图像k与图像k-1之间的时间间隔,为卫星重访周期的整数倍。取M个PS点同一时刻形变量所组成的向量为状态向量,即
| $ {\mathit{\boldsymbol{X}}_k} = {\left( {\mu _k^1,\mu _k^2, \cdots \cdots ,\mu _k^M} \right)^{\rm{T}}}. $ | (10) |
则状态方程为
| $ {\mathit{\boldsymbol{X}}_k} = {\mathit{\boldsymbol{A}}_{k,k - 1}}{\mathit{\boldsymbol{X}}_{k - 1}} + {\mathit{\boldsymbol{B}}_{k,k - 1}}{\mathit{\boldsymbol{u}}_{k - 1}} + {\mathit{\boldsymbol{\xi }}_{k - 1}}. $ | (11) |
其中
| $ {\mathit{\boldsymbol{A}}_{k,k - 1}} = {\mathit{\boldsymbol{I}}_{M \times M}}, $ |
| $ {\mathit{\boldsymbol{B}}_{k,k - 1}} = \left[ {\begin{array}{*{20}{c}} {{b_1}}&{{c_1}}&{{d_1}}\\ \vdots&\vdots&\vdots \\ {{b_M}}&{{c_M}}&{{d_M}} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{u}}_{k - 1}} = \left[ {\begin{array}{*{20}{c}} T\\ {{{\left( {{t_{k - 1}} + T} \right)}^2} - t_{k - 1}^2}\\ {{{\left( {{t_{k - 1}} + T} \right)}^3} - t_{k - 1}^3} \end{array}} \right]. $ |
式中:Ak, k-1为从k-1时刻到k时刻的状态转移矩阵;uk-1为对系统的控制量;Bk, k-1为转换矩阵;ξk-1为状态误差,是对状态转移模型的修正。ξk-1满足以下统计特性:
| $ E\left( {{\mathit{\boldsymbol{\xi }}_{k - 1}}} \right) = 0, $ |
| $ E\left( {{\mathit{\boldsymbol{\xi }}_i}\mathit{\boldsymbol{\xi }}_j^ * } \right) = {\mathit{\boldsymbol{Q}}_\xi }{\delta _{ij}}. $ |
式中:E(·)表示数学期望,Qξ为模型误差协方差矩阵,δij为狄拉克函数,说明不同时刻的模型误差是相互独立的。
2.2 观测方程现在利用卡尔曼滤波的方法处理新增影像,首先新增影像与主影像进行干涉处理,然后利用校正后的DEM去除地形相位得到差分干涉相位(仅对PS点操作),差分干涉相位的相位模型如式(1)所示。
接下来非常关键的一步是估计并去除大气相位的影响,可以通过多幅图像的相位统计特性,利用大气相位在空间域相关、时间域不相关的特点将其分离出来。但是这种方法需要重新处理整个数据集,步骤繁琐、耗时严重。除此之外还可以通过引入外部大气数据来估计大气相位,一种方法是根据SAR成像区域内地基GPS接收器获得的大气延迟数据插值估计大气相位[13];另一种方法是根据近红外探测仪测得的水汽数据估计大气相位,不过研究区域内云的变化情况会对这种方法的精度产生很大影响[14];还有一种方法是通过高分辨率的大气数据模型对成像时刻的大气状况进行预报模拟出大气相位[15]。这几种方法可以在不同程度上减弱大气延迟的影响,但是它们相对比较复杂,而且针对特定研究区域的未必有可用数据。
为充分利用已有数据处理结果,快速估计大气延迟,本文提出一种更为简便的方法。从新产生的差分干涉图中减去线性形变对应的相位(理想情况下线性形变率的精度可以达到0.1~0.5 mm/a[16],如果不发生地震、断层等突变情况,新增一景影像平均形变率不会明显变化),与参考点二次差分去除相位偏移,得到残余相位ω(X)。根据大气相位的时空特性,对残余相位在空域进行高通滤波,然后在时间域进行低通滤波,即通过式(6),估计大气相位的影响。这样既发挥了PS-InSAR利用多景数据统计特性减弱大气扰动影响的技术优势,保证了处理精度;又可以避免重新处理整个数据集,提高了数据处理的效率。
重新将线性形变对应的相位加回差分干涉相位中。然后对差分干涉相位进行相位解缠,由于已经去掉地形相位和大气相位,相位解缠的难度大大降低。式(1)变为如下形式
| $ {\phi ^i} = \phi _{{\rm{topo}}}^i + \phi _{{\rm{defo}}}^i + \phi _{\rm{n}}^i,i = 1, \cdots ,M. $ | (12) |
令观测向量为
| $ {\mathit{\boldsymbol{Z}}_k} = {\left( {\phi _k^1,\phi _k^2, \cdots ,\phi _k^M} \right)^{\rm{T}}}. $ | (13) |
则观测方程可以表示为
| $ {\mathit{\boldsymbol{Z}}_k} = {\mathit{\boldsymbol{C}}_k}{\mathit{\boldsymbol{X}}_k} + {\mathit{\boldsymbol{D}}_k}{\mathit{\boldsymbol{h}}_k} + {\mathit{\boldsymbol{\eta }}_k}. $ | (14) |
其中
| $ {\mathit{\boldsymbol{C}}_k} = - \frac{{4{\rm{ \mathsf{ π} }}}}{\lambda } \cdot {\mathit{\boldsymbol{I}}_{M \times M}}, $ |
| $ {\mathit{\boldsymbol{h}}_k} = {\left[ {\begin{array}{*{20}{c}} {\Delta {h_1}}& \cdots &{\Delta {h_M}} \end{array}} \right]^{\rm{T}}}, $ |
| $ {\mathit{\boldsymbol{D}}_k} = \left[ {\begin{array}{*{20}{c}} { - \frac{{4{\rm{ \mathsf{ π} }}}}{\lambda }\frac{{B_ \bot ^k}}{{{r_1}\sin {\theta _1}}}}& \cdots &0\\ \vdots&\ddots&\vdots \\ 0& \cdots &{ - \frac{{4{\rm{ \mathsf{ π} }}}}{\lambda }\frac{{B_ \bot ^k}}{{{r_M}\sin {\theta _M}}}} \end{array}} \right]. $ |
式中: Ck为k时刻的观测矩阵,hk表示DEM误差对应的向量,Dk为k时刻的转换矩阵,ηk为观测误差。ηk和ξk-1满足以下统计特性:
| $ E\left( {{\mathit{\boldsymbol{\eta }}_{k - 1}}} \right) = 0 $ |
| $ E\left( {{\mathit{\boldsymbol{\eta }}_i}\mathit{\boldsymbol{\eta }}_j^ * } \right) = {\mathit{\boldsymbol{R}}_\eta }{\delta _{ij}}, $ |
| $ \mathit{E}\left( {{\mathit{\boldsymbol{\xi }}_k}\mathit{\boldsymbol{\eta }}_k^ * } \right) = 0. $ |
式中Rη为观测误差对应的协方差矩阵,不同时刻的测量误差相互独立,测量误差和模型误差相互独立。
PS-InSAR校正后的DEM精度很高,误差小于1 m。假设高程误差为1 m,平均垂直基线76 m,实验所用的TerraSAR数据波长3.1 cm,参考图像的中心斜距为565 632.095 5 m,参考图像的雷达入射角为26.423 6°,则由下式可得残余地形相位为
| $ \phi _{{\rm{topo}}}^i = - \frac{{4{\rm{ \mathsf{ π} }}}}{\lambda }\frac{{B_ \bot ^kh}}{{r\sin \theta }} = 0.12{\rm{rad}}. $ |
所以为了简化模型,可以将Dkhk从观测方程中去掉,这时ηk中包含DEM误差的影响,应根据经验估计Dkhk的协方差矩阵对Rη进行调整。
2.3 形变预测通过前一时刻的状态预测当前时刻的状态,初始状态为历史数据最后一幅图像对应时刻的形变向量,状态预测方程为
| $ {{\mathit{\boldsymbol{\hat X'}}}_k} = {\mathit{\boldsymbol{A}}_{k,k - 1}}{{\mathit{\boldsymbol{\hat X}}}_{k - 1}} + {\mathit{\boldsymbol{B}}_{k,k - 1}}{\mathit{\boldsymbol{u}}_{k - 1}} + {\mathit{\boldsymbol{\xi }}_{k - 1}}. $ | (15) |
然后通过前一时刻的状态协方差矩阵预测当前时刻的协方差矩阵,用来表示状态估计的误差,初始协方差矩阵可通过分析PS-InSAR形变量估计精度来确定,状态协方差矩阵的估计方程为
| $ {{\mathit{\boldsymbol{P'}}}_k} = {\mathit{\boldsymbol{A}}_{k,k - 1}}{\mathit{\boldsymbol{P}}_{k - 1}}\mathit{\boldsymbol{A}}_{k,k - 1}^{\rm{T}} - {\mathit{\boldsymbol{Q}}_{k - 1}}. $ | (16) |
由式(16)完成了对未来时刻形变量的预测,uk-1中的时间间隔T可根据实际情况设定。当有新影像加入时,按照上节中的方法获得差分干涉相位,去除大气相位,对预测状态进行校正。首先计算增益矩阵
| $ {\mathit{\boldsymbol{K}}_k} = {{\mathit{\boldsymbol{P'}}}_k}\mathit{\boldsymbol{C}}_k^{\rm{T}}{\left[ {{\mathit{\boldsymbol{C}}_k}{{\mathit{\boldsymbol{P'}}}_k}\mathit{\boldsymbol{C}}_k^{\rm{T}} + {\mathit{\boldsymbol{R}}_k}} \right]^{ - 1}}, $ | (17) |
接下来通过滤波方程对状态向量进行校正
| $ {{\mathit{\boldsymbol{\hat X}}}_k} = {{\mathit{\boldsymbol{\hat X'}}}_k} + {\mathit{\boldsymbol{K}}_k}\left( {{\mathit{\boldsymbol{Z}}_k} - {\mathit{\boldsymbol{C}}_k}{{\mathit{\boldsymbol{\hat X'}}}_k}} \right), $ | (18) |
最后更新状态协方差矩阵
| $ {\mathit{\boldsymbol{P}}_k} = {{\mathit{\boldsymbol{P'}}}_k} - {\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{C}}_k}{{\mathit{\boldsymbol{P'}}}_k}. $ | (19) |
预测协方差矩阵Pk用来衡量状态方程对系统状态预测的不确定性,Pk越小,对测量值的预测就越精确。
3 实验结果和分析讨论 3.1 新奥尔良地表形变预测实验本文采用42景美国新奥尔良地区TerraSAR影像,验证该方法的有效性。首先,利用PS-InSAR技术处理所有影像获取观测区域形变信息,以此作为形变预测精度的对比值。然后处理前35景图像,获取平均形变率、形变量以及校正后的高精度DEM,用本文提出的算法对后7景图像对应时刻的形变量进行预测,与直接用PS-InSAR技术获得的形变量(认为足够精确,视为真实变化值)进行对比,分析形变预测精度。
图 1(a)、1(b)图分别是2012年5月11日形变量的真实值和预测值,通过对比图 1(a)和1(b),可以看出,整体上本文算法预测的形变量与真实形变量非常相似,说明形变预测的效果比较理想。该方法可以预测每一个PS点的形变情况,相对于传统方法在观测区域和观测点密度方面具有明显优势。

|
Download:
|
| 图 1 2012年5月11日真实形变量和预测值 Fig. 1 The real values and predicted values of deformation of 11 May 2012 | |
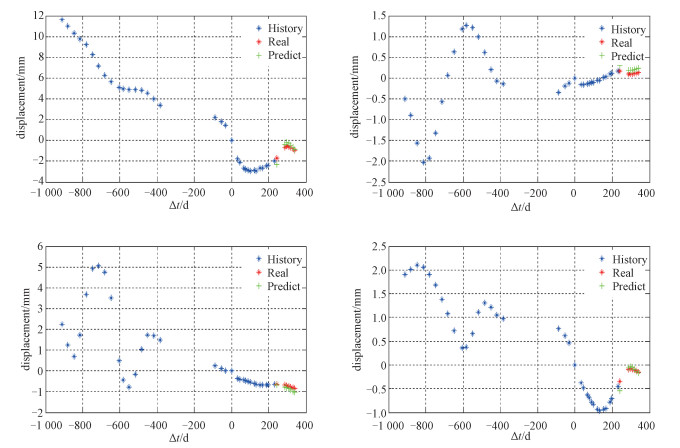
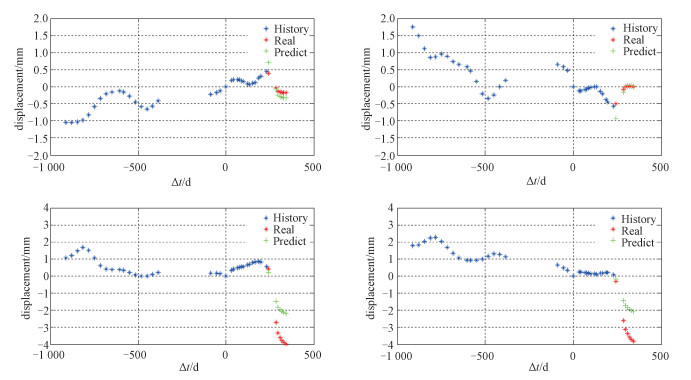
选取图 1中不同形变趋势的PS点在时间维对比预测值和真实值,由图 2可以看出,对于形变趋势比较平稳的点,预测非常准确,偏差很小;由图 3可以发现,对于形变趋势复杂、变化较大或者存在突变的点,预测的误差较大。对于形变趋势复杂的点,可以通过增加多项式的次数拟合更加准确的形变函数,提高形变预测精度。
|
Download:
|
| 图 2 第1组PS点形变量预测值和真实值对比 Fig. 2 Comparison between predicted deformation and real deformation of the first group of PSs | |
|
Download:
|
| 图 3 第2组PS点形变量预测值和真实值对比 Fig. 3 Comparison between predicted deformation and real deformation of the second group of PSs | |
为了从数值上分析该算法形变预测的精度,计算不同时刻形变量预测值的平均偏差,即
| $ \Delta {{\bar \mu }_k} = \frac{1}{M}\sum\limits_i^M {\left| {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \mu } _k^i - \mu _k^i} \right|} . $ | (20) |
从表 1可以看出,形变预测值的平均偏差很小,说明该算法形变预测的效果比较理想。同时可以看出,随着时间的推移,平均偏差越来越大,说明预测短时间内的形变精度较高,而预测长期形变精度会下降。造成这种现象的原因是仅拟合出历史形变函数确定状态方程,而形变函数会随时间发生变化,造成状态方程存在偏差,影响预测精度。因此,为确保长期形变预测的精度,在实际应用中到达一定时间应重新拟合形变函数,更新状态方程。
|
|
表 1 形变预测值平均偏差 Table 1 Mean variation of predicted deformation |
为进一步验证该形变预测方法的有效性,本文进行了北京通州地区地表形变预测精度验证实验。该实验首先利用2013—2016年32景TerraSAR影像获取地面平均沉降速率和SAR影像对应时刻的形变量,进而利用卡尔曼滤波的方法预测2016年4月27日至2016年9月14日期间地表形变信息,重点以观测区域内的温榆河左右桥为研究对象,将形变预测值与水准数据测量结果比对,验证形变预测结果的精度。
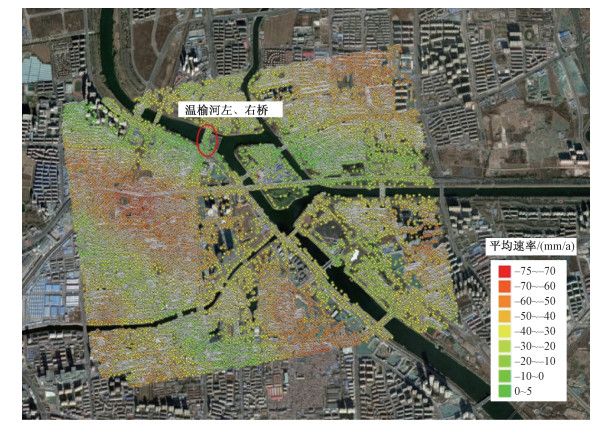
该地区2013—2016年的平均形变速率如图 4所示,图中彩色点表示PS点,并以不同颜色表示相应的形变速率。在大约2 km×2 km的范围内有12万PS点,观测点的数量和密度是常规观测手段无法比拟的。从图中可以发现,通州地面地面沉降情况十分严重,图中红色区域沉降最为严重,沉降速率最高达到-75 mm/a(相对形变),大部分地区沉降速率超过-30 mm/a。从PS点颜色可以发现,温榆河左右桥的南北两端形变情况存在差异,北端沉降速率明显大于南端。
|
Download:
|
| 图 4 通州地区形变信息图 Fig. 4 Displacement of Tongzhou | |
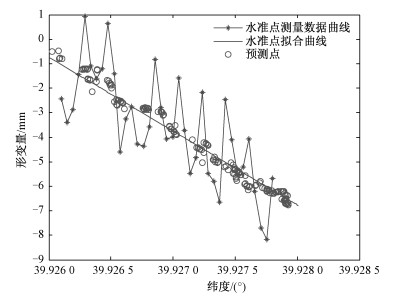
通过2016年4月27日和2016年9月14日两次对温榆河左右桥的水准沉降监测数据,用9月份测量高程减去4月份测量高程计算出两次沉降观测的沉降差,得到这一时期相对沉降量。同时用本文提出的方法预测这段时间的相对形变量,将其与水准数据比对,比对结果如图 5所示。由于水准观测点布设在桥梁的不同位置上,包括桥面观测点、桥墩、台观测点等,桥梁不同结构位置形变情况可能存在差异,桥梁形变受风、温度、车流等影响,另外水准测量数据本身也存在误差,所以水准数据波动较大。为更好地反映桥梁整体形变趋势,将水准数据进行线性拟合。从图中可以看出,水准监测结果和形变预测结果都表明从桥梁南端到北端形变逐渐增大,预测形变值与水准数据观测值趋势相同。水准数据拟合直线表明温榆河左右桥北端较南端的相对沉降量达到约6 mm,而预测值北端相对南端也沉降了大约6 mm,与水准数据拟合直线非常吻合,说明本文方法可准确预测地面目标的形变趋势。
|
Download:
|
| 图 5 温榆河大桥形变量预测值和水准数据对比 Fig. 5 Comparison between predicted deformation and leveling data of the Wenyu River Bridge | |
总体来看,虽然受限于水准点测量中的一些随机因素,以及PS点和水准监测点空间上的不完全匹配,二者测量结果还存在一些的差异,但是扩展卡尔曼滤波预测结果基本和水准测量结果趋势相同,变化情况基本保持一致,充分说明本文方法形变预测信息是可靠、合理的。
4 总结本文提出一种新的基于扩展卡尔曼滤波的PS-InSAR形变预测方法,根据差分干涉相位模型详细推导卡尔曼滤波器的状态方程和观测方程,与PS-InSAR的技术流程相结合建立形变预测的理论模型。该方法充分利用PS-InSAR技术高精度的形变监测结果,得到较高精度、高空间分辨率的形变预测值,适用于大范围的地面形变预测。通过美国新奥尔良地区地面形变预测和北京通州地面形变预测实验,并与水准数据对比,验证了该方法的有效性。虽然该方法对于复杂形变和地面断层等突变情况预测值存在一定误差,但是对于绝大部分观测目标,预测的形变趋势与真实形变趋势相吻合。从与水准数据比对结果来看,预测精度较高,对于地面沉降的治理和预防有重要的参考价值,具有广阔的应用前景。
| [1] | Colesanti C, Ferretti A, Prati C, et al. Monitoring landslides and tectonic motions with the permanent scatterers technique[J]. Engineering Geology, 2003, 68:3–14. DOI:10.1016/S0013-7952(02)00195-3 |
| [2] | Wan Q, Liew S C, Kwoh L K. Permanent scatterer InSAR for ground deformation mapping using ALOS PALSAR data:a case study in Singapore//IEEE International Geoscience & Remote Sensing Symposium, Canada. 2014:441-444. |
| [3] | Zeng Q, Jiao J, Shen L, et al. Measurement crustal movement along Altyn Tagh Fault by using multimode InSAR time series analysis//IEEE International Geoscience & Remote Sensing Symposium, China, 2016:3822-3825. |
| [4] | 陈兴权, 王解先, 谷川. 基于主成分分析的BP神经网络在形变预测中的应用[J]. 大地测量与地球动力学, 2008, 28(3):72–76. |
| [5] | 张卫国, 赵越红. 改进灰色神经网络模型在形变预测中的应用[J]. 计算机仿真, 2016, 33(6):446–450. |
| [6] | 黄国斌, 田林亚, 赵小飞. 径向基神经网络的大桥形变预测[J]. 辽宁工程技术大学学报(自然科学版), 2013, 32(8):1103–1106. |
| [7] | 宁伟, 周立, 宁亚飞, 等. 隧道变形监测预测模型的建立与改正[J]. 东南大学学报(自然科学版), 2013, 43(增Ⅱ):279–282. |
| [8] | Ferretti A, Prati C, Rocca F. Permanent scatterers in SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(1):8–20. DOI:10.1109/36.898661 |
| [9] | Ferretti A, Prati C, Rocca F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5):2202–2212. DOI:10.1109/36.868878 |
| [10] | 刘国祥, 陈强, 罗小军, 等. 永久散射体雷达干涉理论与方法[M]. 北京: 科学出版社, 2012: 52-69. |
| [11] | Chui C K, Chen G. Kalman filtering with real-time application[M]. Berlin: Springer Berlin Heidelberg, 2009: 16-26. |
| [12] | 叶俊华. 基于自适应卡尔曼滤波的灰色模型改进及在变形预测中的应用研究. 西安: 长安大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10710-1013018124.htm |
| [13] | Onn F, Zebker H A. Correction for interferometric synthetic aperture radar atmospheric phase artifacts using time series of zenith wet delay observations from a GPS network[J]. Journal of Geophysical Research, 2006, 111:B09102. |
| [14] | Li Z, Fielding E J, Cross P, et al. Interferometric synthetic aperture radar atmospheric correction:medium resolution imaging spectrometer and advanced synthetic aperture radar integration[J]. Geophysical Research Letters, 2006, 33(6):L06816. |
| [15] | Catalao J, Nico G, Hanssen R, et al. Merging GPS and atmospherically corrected InSAR data to map 3-D terrain displacement velocity[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(6):2354–2360. DOI:10.1109/TGRS.2010.2091963 |
| [16] | Colesant C, Ferretti A, Novali F, et al. SAR monitoring of progressive and seasonal ground deformation using the permanent scatterers technique[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(7):1685–1701. DOI:10.1109/TGRS.2003.813278 |
 2017, Vol. 34
2017, Vol. 34 


