舰船是人类海洋活动的重要工具, 对海上舰船进行遥感监测对于维护国家安全、发展国家经济具有十分重要的意义.然而传统光学遥感容易受到云层和昼夜变化的影响, 而合成孔径雷达(synthetic aperture radar, SAR)却能够全天时、全天候成像, 因而成为舰船监测的重要手段.当SAR对海面运动舰船成像时, 常可观测到4种类型的舰船尾迹:湍流尾迹、开尔文尾迹、窄Ⅴ形尾迹和船生内波尾迹^[1].检测SAR图像中的这些尾迹可以用来反演运动舰船的航速、航向信息, 也有助于发现图像中难以检测的弱小舰船目标^[2].然而, 舰船尾迹能否被SAR设备成像受到船体因素(如舰船吨位和航行状态)、SAR系统因素(如极化方式和工作频率)和海洋因素(如海面风速和海水层化)的影响^[3], 而且, SAR图像中固有的斑点噪声以及高风速下剧烈起伏的海面形态都使得SAR图像舰船尾迹检测非常困难.对于SAR图像舰船尾迹检测的研究可以追溯到20世纪80年代末, 绝大多数方法都从舰船尾迹的形状特点出发, 转化为斑点噪声下的线特征检测问题, 采用基于Radon变换或者Hough变换的线检测方法; 并且为了消除斑点噪声的影响, 一般都会先对图像进行某种形式的滤波预处理和强散射点去除.比如, 文献[2, 4-11]均提出在检测舰船尾迹前先对SAR图像进行预处理, 其中, 文献[2]采用滑动窗滤波方法, 文献[4]采用小波相关器方法, 文献[5]采用随机匹配滤波方法, 文献[6]进行去均值的归一化处理, 文献[7]进行奇异区剔除处理, 文献[8]采用中值滤波方法, 文献[9]采用均值漂移(mean-shift)滤波方法, 文献[10]采用非线性滤波方法, 文献[11]采用西格玛滤波方法; 相反, 文献[12-13]则不主张对图像进行预处理, 而是认为Radon变换或者Hough变换本身即具有斑点噪声抑制能力.而在预处理后的尾迹线检测阶段, 文献[2, 4-5]采用标准Radon变换方法, 文献[6-7]提出并采用长度归一化的Radon变换方法, 文献[8-10]提出并采用窗口Radon变换方法, 文献[13]则提出并采用线段Radon变换方法, 此外, 文献[11-12]提出并且采用灰度归一化的Hough变换方法.

不难看出, 当前的SAR图像舰船尾迹检测方法没有特别考虑图像背景的复杂性, 仅仅认为通过抑制斑点噪声就能够取得好的尾迹检测效果, 因而对于复杂背景SAR图像的尾迹检测效果会很糟糕.因此, 本文从图像能量的角度出发, 针对复杂背景SAR图像提出一种新的舰船尾迹检测方法.该方法通过建立相对全变分能量泛函模型而分离出图像中包含舰船尾迹的光滑成分与包含海面背景纹理的振荡成分, 之后考虑到光滑成分中舰船尾迹表现出方向性的高频特征, 使用剪切波变换求取光滑成分的高频系数并重构部分系数, 再对重构图像做二值化处理得到增强的舰船尾迹图像, 最终通过Radon变换检测出该二值图像中的尾迹线.

1 简单背景与复杂背景的定义及特点分析

海面常被看作海风作用下的随机粗糙面, 由大尺度的近似周期性波浪和小尺度的波纹及浪花叠加而成.随着海风的增大, 海面粗糙度也随之增强, 使得SAR发出的雷达波发生各向异性的散射、并将目标信号淹没其中.由于海杂波在SAR图像上表现为随机纹理的复杂形态, 因此本文即根据这种纹理的粗糙程度定义舰船尾迹的背景复杂程度.当海面背景粗糙程度较低时, 称这样的图像是简单背景的, 如图 1(a)所示, 特点是海面背景亮度较暗但起伏均匀、舰船尾迹较显著.反之则称这样的图像是复杂背景的, 如图 1(b)所示, 特点是海面背景亮度较高且起伏剧烈、舰船尾迹不明显.正是由于简单背景下舰船尾迹较为显著, 因而现有的舰船尾迹检测方法能够取得比较好的检测效果.但是在复杂背景下, 由于舰船尾迹不明显, 现有方法并不能取得理想的检测效果.因此, 本文工作旨在解决复杂背景下的舰船尾迹检测问题.

需要指出的是, 海面SAR图像中除舰船尾迹呈线状特征以外, 往往还存在其他类型的线状目标, 如海洋内波、岛屿边缘、线状溢油等, 增加了背景的复杂性.但是本文只将它们看作检测舰船尾迹的干扰, 会对结果造成影响并产生错检.因此在实际应用中, 尾迹检测后的鉴别处理是必要的, 但这些不是本文的研究内容.

2 图像分解的全变分正则化模型

通常可以将图像X看作由光滑成分S和振荡成分V线性叠加而成, 表示为

$ \mathit{\boldsymbol{X}} = \mathit{\boldsymbol{S}} + \mathit{\boldsymbol{V}}, $

(1)

其中: S包含图像的几何信息, 反映图像逐片光滑的骨架轮廓; V包含图像的细节信息, 反映图像的周期性或振荡本质.可以看到, 从图像X分离出S和V是一个不适定的反问题, 不附加限制条件将没有唯一解.而如果从能量角度出发构建图像的能量泛函E(S, V), 则当其为凸时, 通过求全局极小值即可得到S和V的最终分解结果.这个能量泛函^[14]可以定义为如下形式:

$ E\left( {\mathit{\boldsymbol{S}},\mathit{\boldsymbol{V}}} \right) = E\left( \mathit{\boldsymbol{S}} \right) + \lambda E\left( \mathit{\boldsymbol{V}} \right), $

(2)

其中：E(S)表示S的能量泛函；E(V)表示V的能量泛函；λ表示二者权重.为使E(S, V)为凸的, 常取E(S)为S的全变分(total variation, TV)范数:

$ E\left( \mathit{\boldsymbol{S}} \right) = \sum\limits_{i,j} {\left| {\nabla \mathit{\boldsymbol{S}}} \right|} = {\left\| \mathit{\boldsymbol{S}} \right\|_{{\rm{TV}}}}, $

(3)

即S的梯度矩阵中各元素绝对值的和, 相当于对S进行平滑, 使之接近于图像的真实骨架.另外, 也常将E(V)取为V的某种形式的范数以适配不同类型的纹理, 比如L²范数或者G范数.当E(V)取为V的L²范数时, 求E(S, V)极小值的过程可以表示为如下的最优化问题:

$ \left( {{\mathit{\boldsymbol{S}}^ * },{\mathit{\boldsymbol{V}}^ * }} \right) = \arg \mathop {\min }\limits_{\mathit{\boldsymbol{S}},\mathit{\boldsymbol{V}}} \left( {\lambda \left\| \mathit{\boldsymbol{V}} \right\|_2^2 + {{\left\| \mathit{\boldsymbol{S}} \right\|}_{{\rm{TV}}}}} \right), $

(4)

其中, S^*和V^*表示最优分解得到的S和V.由于V=X-S, 式(4)的右侧括号内又可以表示为

$ \begin{array}{l} E\left( \mathit{\boldsymbol{S}} \right) = \lambda \left\| {\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{S}}} \right\|_2^2 + {\left\| \mathit{\boldsymbol{S}} \right\|_{{\rm{TV}}}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i,j} {\left[ {\lambda {{\left( {\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{S}}} \right)}^2} + \left| {\nabla \mathit{\boldsymbol{S}}} \right|} \right]} , \end{array} $

(5)

其中, (i, j)表示X及S中的像素位置.由于E(S)的值对应$ \frac{\partial E}{\partial \mathit{\boldsymbol{S}}}=F\left( \mathit{\boldsymbol{S}} \right)=\lambda {{\left( \mathit{\boldsymbol{X}}-\mathit{\boldsymbol{S}} \right)}^{2}}+\left| \nabla \mathit{\boldsymbol{S}} \right|=0 $时S的取值, 从而可以推导出关于泛函F(S)的偏微分方程形式^[15]35-63如下:

$ \frac{{\partial F}}{{\partial \mathit{\boldsymbol{S}}}} - \frac{{\rm{d}}}{{{\rm{d}}i}}\left( {\frac{{\partial F}}{{\partial {\mathit{\boldsymbol{S}}_i}}}} \right) - \frac{{\rm{d}}}{{{\rm{d}}j}}\left( {\frac{{\partial F}}{{\partial {\mathit{\boldsymbol{S}}_j}}}} \right) = 0, $

(6)

其中, $ \frac{\partial F}{\partial {{\mathit{\boldsymbol{S}}}_{i}}} $和$ \frac{\partial F}{\partial {{\mathit{\boldsymbol{S}}}_{j}}} $表示泛函F(S)在S的i方向和j方向上的偏导数.式(6)也被称为欧拉-拉格朗日方程, 是一个静态的偏微分方程(partial differential equation, PDE), 可以引入时间变量t而将其转变为一个发展型的PDE:

$ \frac{{\partial \mathit{\boldsymbol{S}}}}{{\partial t}} = - F\left( {\mathit{\boldsymbol{S}}\left( {i,j,t} \right)} \right). $

(7)

对于式(7)的求解, 可将迭代计算次数看作t, 从而将式(7)离散化为代数方程组, 而后即可通过高斯迭代等方法求出使E(S)达到极小值时所对应的S以及V的取值.

3 复杂背景的舰船尾迹检测方法

在复杂背景的SAR图像中, 海面背景呈现出随机纹理的复杂形态, 淹没了舰船尾迹自身的结构形态, 使得现有的舰船尾迹检测方法很难发挥作用.针对这一问题, 本文方法的思路是: 1)对SAR图像采用相对全变分技术进行预处理, 将包含舰船尾迹的光滑成分和包含海面背景纹理的振荡成分相分离; 2)对光滑成分进行剪切波变换, 重构部分高频系数后对重构图像进行二值化处理, 以增强光滑成分中的舰船尾迹区域; 3)对二值化的舰船尾迹区域进行Radon变换, 从而检测出连续的尾迹线.

3.1 光滑成分分离

本小节依据图像分解的全变分正则化模型, 将复杂背景SAR图像X看作是包含舰船尾迹的光滑成分S和包含海面背景纹理的振荡成分V线性叠加而成, 如式(1)所示, 通过全变分方法可以求得唯一解.但是文献[16]指出, 传统全变分方法不能很好区分光滑成分的边缘和纹理成分, 因而提出相对全变分(relative total variation, RTV)图像分解方法.该方法定义像素点p的窗口全变分$ \mathscr{D} $和窗口不相关变分$ \mathscr{L} $(p)如下:

$ \begin{array}{l} {\mathscr{D}_x}\left( p \right) = \sum\limits_{q \in R\left( p \right)} {{g_{p,q}} \cdot \left| {{{\left( {{\partial _x}\mathit{\boldsymbol{S}}} \right)}_q}} \right|} ,\\ {\mathscr{D}_y}\left( p \right) = \sum\limits_{q \in R\left( p \right)} {{g_{p,q}} \cdot \left| {{{\left( {{\partial _y}\mathit{\boldsymbol{S}}} \right)}_q}} \right|} , \end{array} $

(8)

$ \begin{array}{l} {\mathscr{L}_x}\left( p \right) = \sum\limits_{q \in R\left( p \right)} {{g_{p,q}} \cdot \left| {{{\left( {{\partial _x}\mathit{\boldsymbol{S}}} \right)}_q}} \right|} ,\\ {\mathscr{L}_x}\left( p \right) = \sum\limits_{q \in R\left( p \right)} {{g_{p,q}} \cdot \left| {{{\left( {{\partial _y}\mathit{\boldsymbol{S}}} \right)}_q}} \right|} , \end{array} $

(9)

其中: R(p)表示以像素点p为中心的矩形窗口; q表示窗口内的某像素点; ∂_xS和∂_yS表示光滑成分S沿x方向和y方向的梯度. g_{p, q}是加权函数, 相当于一个高斯滤波核, 可以定义为

$ {g_{p,q}} \propto \exp \left[ { - \frac{{{{\left( {{x_p} - {x_q}} \right)}^2} + {{\left( {{y_p} - {y_q}} \right)}^2}}}{{2{\sigma ^2}}}} \right], $

(10)

其中, σ表示该窗口内图像内容的标准差, 通过调整σ的取值可以控制滤波核大小.从而光滑成分S的相对全变分可以定义为

$ {\left\| \mathit{\boldsymbol{S}} \right\|_{{\rm{RTV}}}} = \frac{{{\mathscr{D}_x}\left( p \right)}}{{{\mathscr{L}_x}\left( p \right) + }} + \frac{{{\mathscr{D}_y}\left( p \right)}}{{{\mathscr{L}_y}\left( p \right) + }}, $

(11)

其中, $ \boldsymbol{\epsilon} $是一个足够小的正数, 用以防止分母的值为0.从而, S的能量泛函E(S)可以定义为

$ \begin{align} & \ \ \ \ E\left( \mathit{\boldsymbol{S}} \right)=\lambda \left\| \mathit{\boldsymbol{X}}-\mathit{\boldsymbol{S}} \right\|_{2}^{2}+{{\left\| \mathit{\boldsymbol{S}} \right\|}_{\rm{RTV}}}= \\ & \lambda \sum\limits_{p}{{{\left( {{\mathit{\boldsymbol{X}}}_{p}}-{{\mathit{\boldsymbol{S}}}_{p}} \right)}^{2}}+\left( \frac{{{\mathscr{D}}_{x}}\left( p \right)}{{{\mathscr{L}}_{x}}\left( p \right)+\epsilon }+\frac{{{\mathscr{D}}_{y}}\left( p \right)}{{{\mathscr{L}}_{y}}\left( p \right)+\epsilon } \right)}. \\ \end{align} $

(12)

然而这是一个非凸泛函, 无法求取唯一极小值, 但是可以对‖S‖_RTV进行分解, 得到近似表达式

$ \begin{array}{*{20}{c}} {{{\left\| \mathit{\boldsymbol{S}} \right\|}_{{\rm{RTV}}}} \ne \sum\limits_q {{{\left( {{u_x}} \right)}_q}{{\left( {{w_x}} \right)}_q}{{\left[ {{{\left. {{\partial _x}\mathit{\boldsymbol{S}}} \right)}_q}} \right]}^2}} + }\\ {\sum\limits_q {{{\left( {{u_y}} \right)}_q}{{\left( {{w_y}} \right)}_q}{{\left[ {{{\left. {{\partial _y}\mathit{\boldsymbol{S}}} \right)}_q}} \right]}^2}} ,} \end{array} $

(13)

其中, q表示矩形窗口R(p)内的某个像素点, 在该像素点的x方向和y方向上可以分别定义有关变量u和w, 它们的取值如下:

$ \begin{array}{l} {\left( {{u_x}} \right)_q} = {\left( {{G_\sigma } * \frac{1}{{\left| {{G_\sigma } * {\partial _x}\mathit{\boldsymbol{S}}} \right| + \varepsilon }}} \right)_q},\\ {\left( {{w_x}} \right)_q} = \frac{1}{{\left| {{{\left( {{\partial _x}\mathit{\boldsymbol{S}}} \right)}_q}} \right| + \varepsilon }}, \end{array} $

(14)

$ \begin{array}{l} {\left( {{u_y}} \right)_q} = {\left( {{G_\sigma } * \frac{1}{{\left| {{G_\sigma } * {\partial _y}\mathit{\boldsymbol{S}}} \right| + \varepsilon }}} \right)_q},\\ {\left( {{w_y}} \right)_q} = \frac{1}{{\left| {{{\left( {{\partial _y}\mathit{\boldsymbol{S}}} \right)}_q}} \right| + \varepsilon }}, \end{array} $

(15)

其中:G_σ表示标准差为σ的高斯滤波器, *表示卷积运算.此时, E(S)转变为一个凸泛函, 求其极小值即相当于求以下矩阵的极小值:

$ \begin{array}{*{20}{c}} {{{\left( {{\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{S}}} - {\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{X}}}} \right)}^{\rm{T}}}\left( {{\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{S}}} - {\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{X}}}} \right) + \lambda .}\\ {\left( {\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{S}}^{\rm{T}}\mathit{\boldsymbol{C}}_x^{\rm{T}}{\mathit{\boldsymbol{U}}_x}{\mathit{\boldsymbol{W}}_x}\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{S}}} + \mathit{\boldsymbol{v}}_\mathit{\boldsymbol{S}}^{\rm{T}}\mathit{\boldsymbol{C}}_y^{\rm{T}}{\mathit{\boldsymbol{U}}_y}{\mathit{\boldsymbol{W}}_y}\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{S}}}} \right),} \end{array} $

(16)

其中: v_S和v_X分别是光滑成分S和图像X的向量表达; C_x和C_y是光滑成分S沿着x方向和y方向的Toeplitz矩阵; U_x、U_y、W_x、W_y是4个对角矩阵, 各个对角元素表示为:

$ \begin{array}{l} {\mathit{\boldsymbol{U}}_x}\left[ {i,i} \right] = {\left( {{u_x}} \right)_i},\;\;\;\;{\mathit{\boldsymbol{W}}_x}\left[ {i,i} \right] = {\left( {{w_x}} \right)_i},\\ {\mathit{\boldsymbol{U}}_y}\left[ {i,i} \right] = {\left( {{u_y}} \right)_i},\;\;\;\;{\mathit{\boldsymbol{W}}_y}\left[ {i,i} \right] = {\left( {{w_y}} \right)_i}. \end{array} $

求式(16)极小值的过程可以概括为: 1)将第k次迭代求得的光滑成分S代入式(14)和式(15), 2)将求得的矩阵U_x, U_y, W_x, W_y代入以下公式, 得到新的光滑成分S:

$ \left( {\mathit{\boldsymbol{I}} + \lambda {\mathit{\boldsymbol{L}}^k}} \right) \cdot \mathit{\boldsymbol{v}}_\mathit{\boldsymbol{S}}^{k + 1} = {\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{X}}}, $

(17)

其中: I表示单位矩阵; k表示迭代次数; 而矩阵L^k又可以进一步表示为

$ {\mathit{\boldsymbol{L}}^k} = \mathit{\boldsymbol{C}}_x^{\rm{T}}\mathit{\boldsymbol{U}}_x^k\mathit{\boldsymbol{W}}_x^k{\mathit{\boldsymbol{C}}_x} + \mathit{\boldsymbol{C}}_y^{\rm{T}}\mathit{\boldsymbol{U}}_y^k\mathit{\boldsymbol{W}}_y^k{\mathit{\boldsymbol{C}}_y}. $

(18)

对于图 2(a)所示的一幅ERS-2舰船尾迹SAR图像, 设定各有关参数为λ=0.04、σ=4、$ \boldsymbol{\epsilon} $=0.04, 进行基于相对全变分的图像分解, 4次迭代后分离出的光滑成分和振荡成分如图 2(b)和2(c)所示。可以看到, 通过相对全变分, 图像中的舰船尾迹与海面背景纹理相分离, 消除了斑点噪声和复杂纹理对舰船尾迹结构形态的干扰。

3.2 光滑成分增强

由图 2(b)可以看到, 舰船尾迹表现出很强的方向性高频特征, 但同时也存在着低频背景的干扰。为了增强舰船尾迹的显著性, 本文通过提取并重构光滑成分的剪切波高频系数而对舰船尾迹进行增强, 具体步骤是: 1)对光滑成分进行剪切波变换求得高频系数, 相当于获得光滑成分的边缘信息; 2)重构部分高频系数并二值化重构图像, 得到较为干净的舰船尾迹区域图像。

剪切波变换的基函数表达式^[17]1-38如下:

$ {\varphi _{j,km}}\left( \mathit{\boldsymbol{p}} \right) = {\left| \mathit{\boldsymbol{A}} \right|^{\frac{j}{2}}}\varphi \left( {{\mathit{\boldsymbol{B}}^k}{\mathit{\boldsymbol{A}}^j}\mathit{\boldsymbol{p}} - \mathit{\boldsymbol{m}}} \right), $

(19)

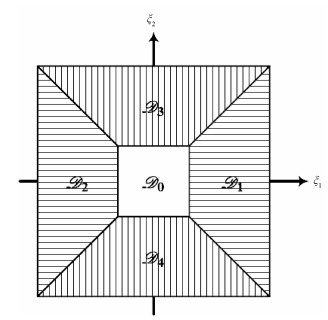
其中:矩阵A称为膨胀因子, 控制变换时的尺度分解; 矩阵B称为剪切因子, 控制变换时的方向分解; 向量m=(m_x, m_y)称为平移因子, 控制卷积运算的范围; 变量j和k分别表示尺度分解数和方向分解数, 而向量p=(x, y)为自变量。各基函数均通过对剪切波函数φ进行尺度、平移和剪切计算而得到。为使各基函数是紧支撑的从而在空间域和频率域中具有细节定位能力, 需要对剪切波函数φ的构成进行限定。可以从频率域出发定义频率域的紧支撑剪切波函数, 这需要将频率平面划分为5个部分, 如图 3所示, 方形区域$ \mathscr{D} $₀为低频盒, 4个梯形区域$ \mathscr{D} $₁~$ \mathscr{D} $₄为高频锥, 且$ \mathscr{D} $₁∪$ \mathscr{D} $₂称为高频水平锥、$ \mathscr{D} $₃∪$ \mathscr{D} $₄称为高频垂直锥。在高频水平锥中, 矩阵A、B定义为:

$ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 4&0\\ 0&2 \end{array}} \right],\mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} 1&1\\ 0&1 \end{array}} \right], $

(20)

而在高频垂直锥中, 矩阵A、B的定义分别为:

$ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 2&0\\ 0&4 \end{array}} \right],\mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} 1&0\\ 1&1 \end{array}} \right]. $

(21)

此时, 记$ \hat{\varphi } $为φ的傅里叶变换, 在高频水平锥和高频垂直锥中分别记为$ \hat{\varphi } $^h和$ \hat{\varphi } $^v, 为使二者是频率域紧支撑的, 可将它们定义为可分离形式:

$ \begin{array}{l} {{\hat \varphi }^{\rm{h}}}\left( \xi \right) = \hat \varphi \left( {{\xi _1},{\xi _2}} \right) = {{\hat \varphi }_1}\left( {{\xi _1}} \right){{\hat \varphi }_2}\left( {\frac{{{\xi _2}}}{{{\xi _1}}}} \right),\\ {{\hat \varphi }^{\rm{v}}}\left( \xi \right) = \hat \varphi \left( {{\xi _2},{\xi _1}} \right) = {{\hat \varphi }_1}\left( {{\xi _2}} \right){{\hat \varphi }_2}\left( {\frac{{{\xi _1}}}{{{\xi _2}}}} \right), \end{array} $

(22)

其中: φ可选频率支撑区间在$ \left[-\frac{1}{2}, -\frac{1}{16} \right]\cup \left[\frac{1}{16}, -\frac{1}{2} \right] $的一元小波, φ₂可选频率支撑区间在[-1, 1]的一元样条, 它们分别是$ \hat{\varphi } $₁和$ \hat{\varphi } $₂的傅里叶逆变换。另外, 记$ \hat{\phi } $为函数$ \phi $的傅里叶变换, 为使$ \hat{\phi } $在低频盒中也紧支撑, 也可将其定义为可分离形式:

$ \hat \phi \left( \xi \right) = \hat \phi \left( {{\xi _1},{\xi _2}} \right) = {{\hat \phi }_1}\left( {{\xi _1}} \right){{\hat \phi }_1}\left( {{\xi _2}} \right), $

(23)

其中, $ \hat{\phi } $₁是$ \phi $₁的傅里叶变换, 可选为m阶盒样条:

$ {{\hat{\phi }}_{1}}\left( w \right)={{\left( \frac{\sin \text{ }\!\!\pi\!\!\text{ }w}{\pi w} \right)}^{m+1}}{{\text{e}}^{-\text{i}\text{ }\!\!\pi\!\!\text{ }\epsilon w}}. $

(24)

经过以上处理即可构建出频率域中紧支撑的剪切波函数, 但是还不能保证其在空间域中也是紧支撑的, 为使其具有空间域的紧支撑性, 还需对函数$ \hat{\varphi } $^h、$ \hat{\varphi } $^v和$ \hat{\phi } $做进一步限定, 使对于常数C₁＞0, C₂＞0和α＞β＞3, 函数$ \hat{\phi } $满足条件

$ \begin{array}{*{20}{c}} {\hat \phi \left( \xi \right) = \hat \phi \left( {{\xi _1},{\xi _2}} \right) \le }\\ {{C_1} \cdot \min \left\{ {1,{{\left| {{\xi _1}} \right|}^{ - \beta }}} \right\} \cdot \min \left\{ {1,{{\left| {{\xi _2}} \right|}^{ - \beta }}} \right\},} \end{array} $

(25)

函数$ \hat{\varphi } $^h和$ \hat{\varphi } $^v满足条件:

$ \begin{array}{*{20}{c}} {\left| {{{\hat \varphi }^{\rm{v}}}\left( {{\xi _2},{\xi _1}} \right)} \right| = \left| {{{\hat \varphi }^{\rm{h}}}\left( {{\xi _1},{\xi _2}} \right)} \right| \le {C_2} \cdot \min \left\{ {1,} \right.}\\ {\left. {{{\left| {{\xi _1}} \right|}^\alpha }} \right\} \cdot \min \left\{ {1,{{\left| {{\xi _1}} \right|}^{ - \beta }}} \right\} \cdot \min \left\{ {1,{{\left| {{\xi _2}} \right|}^{ - \beta }}} \right\}.} \end{array} $

(26)

另外也可以从空间域出发, 选取空间域紧支撑的一元尺度函数$ \phi $₁和小波函数φ₁构建二元函数φ^h, φ^v和$ \phi $。则$ \phi $₁和φ₁应满足双尺度方程:

$ \begin{array}{l} {\phi _1}\left( x \right) = \sqrt 2 \sum\limits_{n \in Z} {h\left( n \right){\phi _1}\left( {2x - n} \right)} ,\\ {\varphi _1}\left( x \right) = \sqrt 2 \sum\limits_{n \in Z} {g\left( n \right){\phi _1}\left( {2x - n} \right)} . \end{array} $

(27)

其中, h(n)和g(n)分别称为低通滤波器和高通滤波器, 二者满足关系式

$ g\left( n \right) = {\left( { - 1} \right)^n}\bar h\left( { - n + 1} \right), $

(28)

其中, h表示h的共轭。从而选择不同的h就可以得到不同的$ \phi $₁和φ₁, 进而得到φ^h, φ^v和$ \phi $:

$ \left\{ \begin{array}{l} \phi \left( {x,y} \right) = {\phi _1}\left( x \right){\phi _1}\left( y \right),\\ {\psi ^{\rm{h}}}\left( {x,y} \right) = {\psi _1}\left( x \right){\phi _1}\left( y \right),\\ {\psi ^{\rm{v}}}\left( {x,y} \right) = {\psi _1}\left( y \right){\phi _1}\left( x \right). \end{array} \right. $

(29)

此时, 剪切波函数是空间域紧支撑的, 若要同时满足频率域的紧支撑性, 只需函数φ^h, φ^v和$ \phi $的傅里叶变换满足条件式(25)和式(26)即可。

经过以上对剪切波基函数的构建, 光滑成分S的剪切波变换可以表示为如下的内积形式:

$ \alpha = \left( {\left\langle {\mathit{\boldsymbol{S}},{\phi _m}} \right\rangle ,\left\langle {\mathit{\boldsymbol{S}},\varphi _{j,k,m}^{\rm{h}}} \right\rangle ,\left\langle {\mathit{\boldsymbol{S}},\varphi _{j,k,m}^{\rm{v}}} \right\rangle } \right), $

(30)

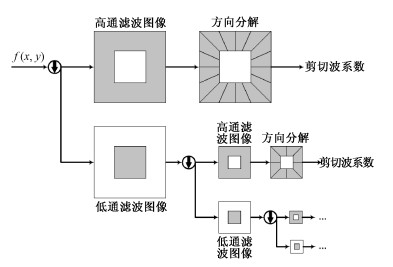
其中: 〈S, $ \phi $_m〉被称为低频剪切波系数, 并且满足$ \phi $_m=$ \phi $(p-m)、p=(x, y)); 同时, 〈S, φ_{j, k, m}^h〉和〈S, φ_{j, k, m}^v〉被称为高频剪切波系数, 且φ_{j, k, m}^h和φ_{j, k, m}^v表示剪切波函数φ^h和φ^v在尺度因子j、方向因子k、平移因子m下的基函数。变换过程中需要进行多分辨率分析并且可以采用空间域和频率域两种方法。前者以卷积计算为基础^[17]239-282, 后者则基于傅里叶变换并包括如图 4所示的4个步骤^[18]: 1)对输入图像进行拉普拉斯变换, 得到一个低通滤波图像和一个高通滤波图像; 2)对高通滤波图像进行傅里叶变换; 3)对变换结果沿不同方向做带通滤波, 得到剪切波系数; 4)将低通滤波图像作为输入再次进行迭代。

图 2(b)所示的光滑成分进行4层剪切波变换, 各层的方向分解数设定为34, 取所得高频系数最大绝对值的0.2倍为阈值T_SC、对高频系数进行阈值化并重构剩余系数, 得到的重构结果如图 5(a)所示, 再对图 5(a)以阈值T_ib=0.3进行二值化, 得到如图 5(b)所示的结果, 即得到一幅比较干净的舰船尾迹区域图像。

3.3 基于Radon变换的尾迹线检测

从图 5(b)可以看出, 二值化的舰船尾迹区域图像通常表现为不连续的线特征, 为了使线特征连续, 本文利用Radon变换对二值图像进行检测。设图像中过像素点(x, y)的直线方程为ρ=x cos θ+y sin θ, ρ表示图像中心到直线的距离, θ表示直线法向与图像x轴正向的夹角。则图像f(x, y)的Radon变换^[2]可以表示为

$ R\left( {p,\theta } \right) = \sum\limits_{x = 1}^M {\sum\limits_{y = 1}^N {f\left( {x,y} \right)\delta \left( {\rho - x\cos \theta - y\sin \theta } \right)} } , $

(31)

其中, δ为Dirac函数, 当像素点在该直线上时δ=1, 否则δ=0。该变换将直线上像素点的灰度值累加, 从而将直线与变换点建立起对应关系。当确定变换域峰值点位置坐标(ρ₀, θ₀)后, 代入直线方程x cos θ₀+y sin θ₀=ρ₀便可绘制出图像域直线, 即舰船尾迹的检测结果。

对图 5(b)所示的二值图像进行Radon变换, 得到图 6(a)所示的结果, 图 6(b)是对图 6(a)按照阈值T_rb=0.6进行二值化处理得到的峰值点检测结果。通过对图 6(b)中的峰值点进行聚类分析并将聚类中心做逆Radon变换, 然后再将变换结果与原图叠加, 即得到图 6(c)中加粗白线所示的舰船尾迹检测结果。

4 实验结果与分析

为验证本文所提方法的性能, 这里使用21幅复杂背景的ERS-2舰船尾迹SAR图像, 在CPU主频3 GHz、内存大小8 GB的windows电脑上采用matlab编程进行性能比较实验。这些图像的方位向空间分辨率与距离向空间分辨率均为12.5 m、尺寸均为300像素×400像素, 共包含有湍流尾迹、开尔文尾迹和窄Ⅴ形尾迹或者尾迹臂32条。这些图像是由欧洲航天局发射的第2颗欧洲遥感卫星所拍摄, 该卫星携带的SAR设备以垂直极化方式对地球大气、陆地、海洋和极地冰进行观测, 已于2011年退役。

实验中, 本文选择文献[6]和文献[11]方法作为性能比较的对象, 分别简记为NRT方法和NHT方法。这2种方法分别采用分块和滤波预处理方法改善尾迹线的检测能力, 体现了当前SAR图像舰船尾迹检测的最优水平。对于本文所提方法, 涉及的重要参数有8个, 分别是:图像分解时的权重系数λ、标准差σ和足够小的正数$ \boldsymbol{\epsilon} $, 光滑成分增强时的剪切波变换层数j、各层的方向分解数k、高频系数的重构阈值T_SC和重构图像的二值化阈值T_ib, 以及尾迹线的检测阈值T_rb, 它们共同构成一个参数组。为缩小最优参数组的搜索空间, 本文采用先根据经验选取参数组的若干合理取值范围, 再以手动调整方式逐步优化的基本思路。具体优化过程是: 1)根据经验选取参数组的3个合理取值范围; 2)在该范围内按一定步长细化调整参数组取值, 统计所有实验样本的查全率(recall, R)和查准率(precision, P), 将这2项指标最高时对应的参数组作为候选最优参数组; 3)将2项指标下3个候选最优参数组中的最优者作为最优参数组。对于NHT方法, 涉及的重要参数为虚警概率P_fa, 它决定了Hough域的检测阈值; 而NRT方法的重要参数为变换域阈值T_r。采用上述步骤也可以确定这2种方法各自的最佳参数。当求得全部3种方法在各自最佳参数下的查全率和查准率后, 便可将这2项指标均最高的方法看作是最佳的舰船尾迹检测方法。这里, 查全率和查准率的计算方法^[19]如下:

$ R = \frac{{{P_t}}}{{{P_n}}},P = \frac{{{P_t}}}{{{P_t} + {P_f}}}, $

(32)

其中：R_t表示检测到的舰船尾迹数; P_f表示检测结果中的非尾迹数; P_n表示舰船尾迹的总数。

最优参数下的部分舰船尾迹检测结果如图 7所示。图 7(b)中的加粗白线表示舰船尾迹的真实位置, 这是专家给出的检测结果, 可用于定量评价这3种方法的查全率和查准率指标, 也可以通过其空间位置对这3种方法的定位精度加以定量评价。图 7(c)~图 7(e)中的白线表示这3种方法对舰船尾迹的检测结果。由图 7(c)和图 7(d)不难看出, 复杂海况背景下, NRT和NHT方法检测出的舰船尾迹大多偏离了真实位置, 错检和漏检情况较为严重。由图 7(e)可以看出, 本文所提方法对于湍流尾迹以及窄Ⅴ形尾迹均表现出更好的检测性能, 这是因为本文所提方法不仅能较好地去除复杂海面背景和斑点噪声对舰船尾迹结构形态的干扰, 而且能够有效提升舰船尾迹的显著程度, 从而得到更准确的检测结果。表 1列出本文所提方法与其他2种方法的查全率和查准率定量比较结果, 可以看到, 本文所提方法的查全率和查准率均高于其他2种方法, 进一步说明该方法的舰船尾迹检测性能远优于NRT和NHT方法。

5 结论

SAR图像舰船尾迹检测是一个极有意义却非常困难的问题, 现有的SAR图像舰船尾迹检测方法对于简单海面背景的情况检测效果比较好, 但在复杂的海面背景情况下检测效果难以满足使用要求。本文从图像能量的角度出发, 提出一种基于相对全变分正则化的复杂背景SAR图像舰船尾迹检测方法。该方法将复杂背景SAR图像看作是由包含舰船尾迹的光滑成分和包含复杂海面背景纹理的振荡成分线性叠加而成, 通过分离出光滑成分并利用剪切波变换和二值化处理对光滑成分进行增强, 可以得到比较干净的二值化舰船尾迹区域图像, 最后再基于Radon变换对该二值图像进行线检测, 即可得到舰船尾迹的线检测结果。与现有舰船尾迹检测方法的比对实验结果表明, 本文所提方法对于复杂背景SAR图像的舰船尾迹的检测效果明显优于参与比较的其他方法。