2. 中国科学院大学, 北京 101408;
3. 安徽师范大学国土资源与旅游学院, 安徽 芜湖 241000
2. University of Chinese Academy of Sciences, Beijing 101408, China;
3. College of Territorial Resources and Tourism, Anhui Normal University, Wuhu 241000, Anhui, China
交通运输作为克服空间摩擦,缩小时间距离的重要手段,在推动区域发展,重塑经济地理格局中起着重要的作用。作为运输系统的核心,效率是政府政策制定及企业运营决策中考虑的关键因素[1],运输效率体现了运输系统的运行状况及发展潜力[2],不仅影响中国交通运输业的可持续发展,而且对整个国民经济的良性发展也产生着不可忽视的影响[3]。而公路运输作为交通运输体系中的重要组成部分[4],相比于其他交通方式具有基础性和普适性,其效率高低对于综合运输体系总体效率产生着重要影响,因此,对公路交通运输效率进行科学、合理的评价极有必要。
就运输效率而言,国外学者较早开展了相关研究,早在20世纪70年代国外学者就对城市公交系统效率及其评价指标进行了研究[5-7]。Levinson[8]从运输的流动性、生产性、效用性和可达性4个维度出发,在不同侧面构建指标对本国运输效率进行评价;Karlaftis和Tsamboulas[9]利用欧洲交通系统15年的数据,构建评估模型,对运输效率不同评价方法的结果进行比较研究;Jain等[10]结合DEA方法,以城市轨道运输系统效率为例,认为私有化对于提升效率有直接和积极的意义。国内就运输效率也进行过很多研究[11-12],吴群琪等[13]借助主成分分析运用超效率三阶段DEA模型探讨中国各省域综合运输效率的空间布局和集群状况。李涛等[14]选取4个时间段综合考虑公路、铁路和水运3种运输方式,分析中国31个省综合运输效率的时空动态变化特征。总体来看,已有研究取得了许多有价值的成果,对交通运输规划和布局具有一定的借鉴意义,但运输效率的测算仍存在一些不足,在研究内容上多从整体上分析运输效率的主要因素,缺少对运输效率的时空演变规律和区域差异的研究。研究方法上多采用传统DEA方法,很少将其他模型应用到运输效率的测度上。
长江三角洲地区(以下简称为长三角地区)是中国区域经济最为发达的地区,也是率先推进区域一体化的地区。低成本、高效率实现区域运输联系是促进该地区一体化及经济社会进一步发展的基础。目前,长三角地区已形成多种交通方式并存的综合交通体系,综合运输成本总体已处于较低水平[15],但人们尚未认识并掌握其运输效率运行的内在机理。而公路运输作为该地区交通运输结构体系中的核心,在其中起着重要的作用,但对其研究涉及较少。
鉴于此,本研究应用DEA方法中的BCC模型结合超效率模型对长三角地区2014年16个城市的公路交通效率进行静态比较。同时采用Malmquist指数模型对长三角地区2014年公路运输技术效率变动、技术进步变动与全要素生产率的关系做进一步的分析,全面分析2007—2014年长三角地区公路运输全要素生产率的时空演变规律与区域差异。以期为该地区公路的投资建设以及整个交通运输业的可持续发展提供一定的科学依据。
1 研究方法与指标体系 1.1 DEA基础模型的建立数据包络分析(data envelopment analysis,简称DEA)是一种用来评价一组具有多输入多输出的决策单元的相对效率的数学规划方法。目前使用较多的模型主要有CCR (Charnes, Cooper, Rhodes)和BCC (Banker, Charnes, Cooper)模型。CCR又称CRS(creasing returns to scale,即规模报酬不变)模型,它计算的是假定规模报酬不变的情况下的效率评价模型。BCC又称VRS(varying returns to scale,即规模报酬变动)模型,能把CCR模型中的综合技术效率分解成规模效率和纯技术效率的乘积。二者的值越接近于1,表示纯技术效率、规模效率越高。当二者都等于1时,表示该城市分别达到纯技术效率最优和规模效率最优。考虑到运输需求的派生性,本文主要选用投入导向的BCC模型,即在不改变产出数量的情况下,可以节约多少投入要素。
超效率模型方法的基本原理与DEA相同,其基本思想是在进行第k个决策单元效率评价时,使第k个决策单元的投入和产出被其他所有的决策单元投入和产出的线性组合替代,而将第k个决策单元排除在外,因而其超效率值可能大于1,即一个有效的决策单元可以使其投入按比例增加,而效率值保持不变,其投入增加比例即其超效率评价值[16]。
1.2 Malmquist生产率指数模型方法Malmquist生产率指数是基于DEA模型的方法提出的,它利用距离函数的比率来计算投入产出效率。公式如下
| $ \begin{align} &{{M}_{i, t+1}}\left( x_{i}^{t}, y_{i}^{t}, x_{i}^{t+1}, y_{i}^{t+1} \right)= \\ &\ {{\left[\frac{D_{i}^{t}\left( x_{i}^{t+1}, y_{i}^{t+1} \right)}{D_{i}^{t}\left( x_{i}^{t}, y_{i}^{t} \right)}\cdot \frac{D_{i}^{t+1}\left( x_{i}^{t+1}, y_{i}^{t+1} \right)}{D_{i}^{t+1}\left( x_{i}^{t}, y_{i}^{t} \right)} \right]}^{1/2}}, \\ \end{align} $ | (1) |
式中:Dt(xt, yt), Dt(xt+1, yt+1)分别指以t期的技术为参考(即以t期的数据为参考集)时,t期和t+1期的决策单元的距离函数,M表示全要素生产率指数,当M > 1时表示生产率水平提高;M=1时表示生产率水平不变;M < 1时表示生产率水平下降。
| $ \begin{align} & {{M}_{i,t+1}}\left( x_{i}^{t},y_{i}^{t},x_{i}^{t+1},y_{i}^{t+1} \right)= \\ & \ \underbrace{\frac{D_{i}^{t+1}\left( x_{i}^{t+1},y_{i}^{t+1} \right)}{D_{i}^{t}\left( x_{i}^{t},y_{i}^{t} \right)}}_{\text{EC}}\underbrace{{{\left[ \frac{D_{i}^{t}\left( x_{i}^{t},y_{i}^{t} \right)}{D_{i}^{t+1}\left( x_{i}^{t},y_{i}^{t} \right)}\cdot \frac{D_{i}^{t}\left( x_{i}^{t+1},y_{i}^{t+1} \right)}{D_{i}^{t+1}\left( x_{i}^{t+1},y_{i}^{t+1} \right)} \right]}^{1/2}},}_{\text{TC}} \\ \end{align} $ | (2) |
式(2)是式(1)的变形,用来表示技术进步变化与技术效率变化的分离。右边前半部分为技术效率变化率(EC),后半部分为技术进步率(TC)。
全要素生产率指数表示道路运输资源的配置、利用水平和规模集聚水平的变化,技术进步指数表示运输技术水平变化情况,技术效率变动指数反映现有生产能力的利用水平。其中包括纯技术效率变动指数和规模效率变动指数。前者表示在技术和规模不变的前提下道路运输相对生产效率的变化,而规模效率反映的是规模集聚水平的变化。
1.3 指标体系与数据来源在有关学者研究的基础上,结合公路运输的实际情况以及数据的可获得性,最终确定投入和产出指标。投入指标包括公路里程(X1)、公路营业性运输车辆拥有量(X2)和公路运输从业人员(X3)。公路里程代表公路资源的投入。营业性运输车辆拥有量代表运输工具的投入水平,主要包括营业性载客汽车和营业性普通载货汽车,其中杭州、绍兴、舟山营业性汽车由于没有直接的统计资料,而营业性汽车一般以大中型汽车为主,所以本文采用的是民用汽车大中型载货汽车和载客汽车来替代。从业人员数是在统计数据的基础上通过一定的计算方法获得的,代表劳动力方面的投入。产出指标包括公路客运量(Y1)、公路客运周转量(Y2)、公路货运量(Y3)和公路货运周转量(Y4)。由于交通运输部分别于2008年和2013年开展了全国公路运输量专项调查,且统计口径有所差别,所以4项产出指标的数据是通过同增长率修正方法修正后的数据。其推算公式为:
| $ {{r}_{i}}={{Y}_{i}}/{{Y}_{i-1}}, $ | (3) |
| $ {{{Y}'}_{i-1}}={{{Y}'}_{i}}/{{r}_{i}}, $ | (4) |
式中:ri为第i年营业性公路运输量增长率;Yi、Yi-1分别为第i、i-1年原统计口径运输量;Y′i、Y′i-1分别为第i、i-1年新统计口径运输量。
以上原始数据来自于长三角地区各地方统计年鉴。
2 结果和分析 2.1 长三角地区公路运输效率分析综合效率反映在最合适的规模下以给定的产出进行运营最大程度节约投入资源的能力,只有当决策单元同时处于技术有效和规模有效时才为综合有效。从表 1可以看出,2014年长三角地区公路运输平均综合效率为0.954,表明长三角地区公路运输平均存在4.6%的投入浪费,总体效率较高。上海、南京、无锡、苏州、宁波、嘉兴、湖州、绍兴、舟山、台州10个城市综合效率DEA有效,综合效率高,投入利用较为充分。分区域来看,北部地区的上海和江苏板块9个城市中,有4个DEA有效,南部浙江板块7个城市除杭州外,其他6个均达到DEA有效。比较DEA无效的城市可知,江苏省有3个低于平均水平,特别是扬州市,综合效率仅为0.65,投入浪费达到35%,可见长三角地区公路运输综合效率存在着一定的地区差异性,南北分异突出,其中南部地区明显高于北部地区。
|
|
表 1 2014年长三角各城市综合效率及分解的特征分析 Table 1 Overall efficiency analysis and decomposition characteristics(2014) |
利用超效率模型对各个地区的运输效率做进一步的评价分析,可以发现苏州市的效率值为2.473,位列第1位,舟山、台州、湖州分别位居第2、3、4位,上海位列第5位,说明在DEA有效的单元中,南部的公路运输效率依然优于北部。因此北部地区应加大对公路运输的重视程度,从而提高整个地区的公路交通运输效率。
由表 1可以看出,DEA无效的6个城市,其规模效率也是无效的,说明2014年长三角地区规模效率是决定其综合效率是否有效的主要因素。常州、扬州、镇江、泰州处于规模收益递增阶段,也就是说增加要素投入可以带动公路运输综合效率的提高,政府可通过扩大规模或范围来提高该地区的运输效率,从而使得各地区均衡协调发展。南通、杭州处于规模收益递减阶段,表明增加要素投入并不能提高综合效率。除此之外,镇江、泰州、杭州的技术效率为1,表明该地区的投入产出已经实现最优化,综合效率的无效主要是由于没有实现规模的最优化。而常州、南通、扬州技术效率未达到DEA有效,具有投入冗余或产出不足的现象。
投入冗余和产出不足能客观反映出公路运输技术效率无效的影响因素。由表 2可以看出,常州市主要存在运输车辆的投入冗余和公路客运量的产出不足,2014年常州市运输车辆达到57 727.47辆,存在一定的投入浪费,如果让这些投入达到理想效果,再进一步刺激对公路客运量的需求,将会更有利于常州市交通业的可持续发展。南通市主要存在公路客运量的产出不足和公路里程及运输车辆的冗余,其中公路里程冗余现象较为明显,冗余度达到34.65%,因此南通市应加大对公路资源的利用,从而带动整个公路运输效率的提高。扬州市的技术效率为0.747,远远低于平均水平,存在严重的投入冗余和产出不足现象。扬州市拥有运输车辆45 169.87辆,但这些投入并未达到最佳利用效果,存在投入冗余。产出不足主要表现在公路客运量和货运量指标上,不足量和不足率分别为2 478.701万人、1 611.502万t和51.7%、24.8%,也是影响扬州公路运输效率的主要因素。
|
|
表 2 2014年长三角地区各市公路运输投入冗余产出不足评价结果 Table 2 Evaluation results of input redundancy and output deficiency(2014) |
通过对2007—2014年长三角地区各城市公路运输Malmquist生产率指数分析,得到各年全要素生产率及其分解结果(表 3)。
|
|
表 3 2007—2014年长三角地区Malmquist生产率指数及分解 Table 3 Malmquist efficiency index and its decomposition(2007—2014) |
Malmquist指数反映全要素生产率的变化情况。从长三角地区Malmquist生产率指数的总体水平来看,2007—2014年公路运输的全要素生产率指数呈现一定的波动,总体较为稳定。其中2007、2011、2013、2014年Malmquist指数低于1,其生产率是降低的,但是从整体上看,在本文的研究时段内,Malmquist生产率指数均值为1.016,公路运输的全要素生产率变化是正向的,并以1.6%的年均速度增长。
Malmquist指数通常受技术效率变化和技术进步变化的影响,通过表 3可以看出,2007、2011、2014年3个年份内技术效率和技术进步的同时下降导致该时段内Malmquist指数的下降,全要素生产率较上一年分别下降4.6%、5.5%和6.1%。2008、2010两个年份内,Malmquist指数分别为1.124和1.034,生产率较上一年上升12.4%和3.4%,主要得益于技术效率和技术进步的同时上升。2009、2012年Malmquist指数出现增长,主要得益于技术进步的提升,不仅抵消了技术效率的负增长,还带动了Malmquist指数的提升。2013年技术进步提升3%,技术效率下降3.9%,技术效率的下降带动了Malmquist指数的小幅下降,其全要素生产率较与前一年基本持平。
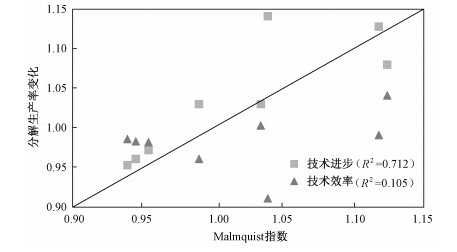
图 1显示的是2007—2014年Malmquist指数与技术效率变化和技术进步变化的二维有序坐标散点图,散点图越集中于45°线,则该因素对全要素生产率变化的解释能力越强,反之则越弱。由图可知,技术进步变化与Malmquist指数拟合程度较高,R2达到0.712,表明技术进步指数对Malmquist指数具有决定性的作用。而技术效率变化与Malmquist指数的拟合程度较差,二者相关系数为0.105,对全要素生产率变化影响不大。
|
Download:
|
| 图 1 2007—2014年各分解生产率变化与全要素生产率变化关系 Fig. 1 Correlations of the decomposed productivity changes with TFP change | |
综上所述,技术进步变化趋势与Malmquist指数变化趋势基本相同。技术进步的快慢直接影响到全要素生产率的增长快慢。这说明长三角地区公路运输效率的提高依靠技术进步是行之有效的方法,而技术效率的变化起着减缓和促进全要素生产率增长的作用。
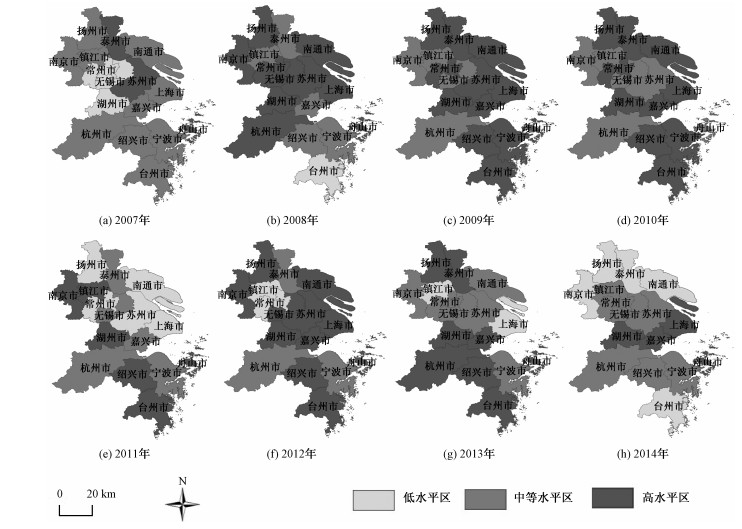
基于DEA-Malmquist模型分析结果,利用2007—2014年长三角地区各城市的Malmquist生产率指数值,运用Arcgis软件对其进行空间分析,将其按大小分为3类,并绘制成空间分布图(图 2)。其中,高水平区的Malmquist指数大于1,全要素生产率与上年相比有所提升,中等水平区Malmquist指数介于0.9~1,全要素生产率与上年相比有所下降但变化不大,低水平区Malmquist指数小于0.9,生产率有较大幅度下降。
|
Download:
|
| 图 2 长三角地区各城市Malmquist生产率指数的时空格局演化过程(2007—2014) Fig. 2 Evolution of temporal and spatial patterns in Malmquist productivity index(2007—2014) | |
从图 2中可以看出,2007年Malmquist指数中等水平区覆盖范围广且集中连片分布,说明长三角地区2007年道路运输全要素生产率相比于2006年总体变化不大。低水平区和高水平区除湖州和舟山外,均位于北部江苏板块,说明该地区全要素生产率变化区域差异明显。从2008年起,全要素生产率开始有明显提升,2008—2010年3年内除2008年的台州外,Malmquist指数均处于中等水平区和高水平区,其中高水平区的城市占绝大多数区域,特别是2009年有12个城市处于高水平区。整个地区全要素生产率进步较快,变化的区域差异不明显,各地区均衡发展。2011—2013年3年内,Malmquist指数空间格局发生明显变化,整体上看各等级的城市分布较为分散,各类型区的城市交叉分布,低水平区主要分布在北部上海和江苏板块,该地区区域差异较大。2014年Malmquist指数整体较低,南北分异突出。低水平区有南京、扬州、泰州、南通、台州5个城市,全要素生产率水平下降,中等水平区和高水平区集中连片分布,主要集中在区域中部。
综上所述,2007—2014时间段内长三角地区全要素生产率的变化存在时空演变规律与区域差异。2007—2010年Malmquist指数在不断上升,区域差异较小,全要素生产率整体水平有所提升,且各地区均衡发展。2010—2013年,不同等级Malmquist指数分布分散,区域差异变大,全要素生产率提升不足且发展不均衡,其中北部的上海和江苏板块差异最为显著,说明北部各地区的要素资源利用配置和规模集聚水平差异较大,个别地区道路交通技术进步不明显,从而影响整个地区全要素生产率的提升。2014年Malmquist指数呈现一定的南北分异特征,区域中部地区全要素生产率进步较快,而南部和北部进步缓慢。说明上海、苏州等经济发达地区开始重视公路运输的发展,在组织创新和技术创新等方面具有较大的进步。
3 结论与讨论1) 长三角地区2014年公路运输综合效率整体水平较高,为长江经济带和长三角城市群发展战略的深入落实提供了重要的推动力量。但是地区间差异仍然明显,南北分异突出,其中规模效率的差异是造成其地区间差异的主要因素。未来如何通过加强公路交通运输的规模效应来减小地区间差异将成为长三角地区提高综合效率、优化空间结构的关键点。
2) 运输车辆的投入冗余和客运量的产出不足是造成常州、南通和扬州技术无效的主要因素。伴随着社会经济的快速发展,各政府对物流业的扶持力度也在不断加大,从而引导公路运输资源包括人员、车辆在内的集聚不断加强,超出当地对公路运输的需求水平,加上对运输资源低效的配置利用,使得技术效率并未达到有效状态。未来该城市需充分刺激对公路客运量的需求,对运输车辆进行高效配置利用,从而提高当地的技术效率。
3) 2007—2014年长三角地区公路运输的全要素生产率指数在波动中缓慢上升,其变化趋势与公路运输行业技术进步指数变化趋势基本相同,说明长三角地区公路运输效率的提高依靠技术进步是行之有效的方法。随着信息革命的深入发展,各地区通过促进公路运输与信息技术的结合来加快技术进步的步伐,将成为提高公路运输生产率的重要举措。
4) 从时空演化来看,长三角地区全要素生产率的变化存在时空演变特征与区域差异。2007—2014年全要素生产率指数先提升后下降,区域差异先缩小后增大。其中南部的区域差异要小于北部地区。
从公路运输投入产出的多样性来考虑,指标的选取应充分反映公路运输的各个方面。针对投入,不仅包括人员、车辆、能源、公路、场站枢纽等物化要素,还应考虑管理、技术等组织要素;产出方面,除考虑公路运输的直接产出——运输服务效益外,还应考虑相应的外部效应,比如事故损失、运输时间、生态环保等。而鉴于数据来源的现状,本文在投入产出指标的选取上具有不全面性,同时由于不同年份统计口径的调整,本文部分数据经过一定方法计算获得,因此得出的结果也存在一定的偏差,有待进一步改善。
| [1] | 杨良杰, 吴威, 苏勤, 等. 基于SBM-Undesirable模型的1997-2010年中国公路运输效率评价[J]. 地理科学进展, 2013, 32(11):1602–1611. DOI:10.11820/dlkxjz.2013.11.003 |
| [2] | Costa A, Markellos R N. Evaluation public transport efficiency with neural network models[J]. Transportation Research Part C:Emerging Technologies, 1997, 5(5):301–312. DOI:10.1016/S0968-090X(97)00017-X |
| [3] | 吴威, 曹有挥, 梁双波. 运输效率研究述评及基于交通运输地理学视角的研究展望[J]. 地理科学进展, 2013, 32(2):243–250. DOI:10.11820/dlkxjz.2013.02.010 |
| [4] | 唐常春, 樊杰, 黄梅. 长株潭城市群公路交通与区域协调发展研究[J]. 地域研究与开发, 2011, 30(2):91–95. |
| [5] | Gilbert G, Dajani J. Measuring the performance of transit service[M]. Chapel Hill, North Carolina: University of North Carolina Press, 1975: 35-65. |
| [6] | Tomazinis A R. A study of efficiency indicators of urban public transportation systems. Washington, DC:United States Department of Transportation (USDOT), 1977:299. http://trid.trb.org/view/54813 |
| [7] | Fielding G J, Glauthier R E, Lave C A. Performance indicators for transit management[J]. Transportation, 1978, 7(4):365–379. DOI:10.1007/BF00168037 |
| [8] | Levinson D. Perspectives on efficiency in transportation[J]. International Journal of Transport Management, 2003, 1(3):145–155. DOI:10.1016/j.ijtm.2004.01.002 |
| [9] | Karlaftis M G, Tsamboulas D. Efficiency measurement in public transport:Are findings specification sensitive?[J]. Transportation Research Part A:Policy and Practice, 2012, 46(2):392–402. DOI:10.1016/j.tra.2011.10.005 |
| [10] | Jain P, Cullinane S, Cullinane K. The impact of governance development models on urban rail efficiency[J]. Transportation Research Part A:Policy and Practice, 2008, 42(9):1238–1250. DOI:10.1016/j.tra.2008.03.012 |
| [11] | 李雪, 吴芳, 左建伟. 兰州市交通运输效率的评价分析[J]. 交通科技与经济, 2007(3):92–94. |
| [12] | 段新, 岑晏青, 路敖青. 基于DEA模型的31省份公路运输效率分析[J]. 交通运输系统工程与信息, 2011, 11(6):25–29. |
| [13] | 吴群琪, 宋京妮, 巨佩伦, 等. 中国省域综合运输效率及其空间分布研究[J]. 经济地理, 2015, 35(12):43–49. |
| [14] | 李涛, 曹小曙, 杨文越, 等. 中国区域综合运输效率的测度及其时空演化[J]. 地理科学, 2015, 35(2):168–175. |
| [15] | 吴威, 曹有挥, 梁双波. 外部成本对区域综合运输成本空间格局的影响:以长江三角洲地区为例[J]. 地理科学, 2011, 31(11):1322–1328. |
| [16] | 李洁, 左毅刚. 基于超效率DEA方法的公路运输效率评价与分析[J]. 交通信息与安全, 2015, 33(1):127–132. |
 2017, Vol. 34
2017, Vol. 34 


