2. 西安科技大学通信与信息工程学院, 西安 710054;
3. 长沙理工大学交通运输工程学院, 长沙 410004
2. College of Communication and Information Engineering, Xi'An University of Science and Technology, Xi'an 710054, China;
3. School of Traffic and Transportation Enginneering, Changsha University of Science & Technology, Changsha 410004, China
干涉合成孔径雷达(InSAR,interferometry synthetic aperture radar)技术是利用两个通道的回波数据经过成像处理产生干涉相位,进而利用干涉信号处理根据干涉几何关系反演出场景DEM(digital elevation model)[1]。该技术经过几十年的发展,已经较为成熟,可以获取较高的DEM精度。目前,机载干涉SAR可以获取优于0.5 m精度的DEM,有的甚至达到0.1 m,国内已经拥有DEM精度优于0.3 m的系统[2];星载干涉SAR系统(TandEM-X系统)目前可以获取绝对高程精度优于10 m和相对高程精度优于2 m的DEM产品[3][4]。由于InSAR系统可实现全天时、全天候对地面大范围、高精度测绘,获得波长量级精度的DEM,使其在地形测绘、形变监测等方面得到了广泛应用[5]。
目前对获取的两通道SAR数据进行成像处理采用较多的是ECS成像算法[6]、改进的ECS自配准[7]及ECS非线性自配准成像算法[8]。但在利用该算法成像中,进行了一些近似和假设,这对干涉相位会造成一定的影响,从而造成DEM精度的降低。
本文通过对非线性ECS自配准成像算法中的相位保持精度进行分析,明确哪些近似或假设可以忽略,哪些需要考虑并对算法改进,从而在本质上解决SAR成像算法引起的DEM精度恶化问题。
1 InSAR技术生成DEM基本原理图 1给出双天线InSAR系统几何关系图。由该图可得DEM反演公式[8]
| $ \begin{array}{l} {\theta _1} \approx \alpha - \arcsin \left( {\lambda \varphi /2{\rm{\pi }}BQ} \right),\\ h = H - r\cos {\theta _1},\\ y = r\sin {\theta _1}. \end{array} $ | (1) |

|
Download:
|
| 图 1 干涉几何关系图 Fig. 1 Interferometry geometry relations | |
由(1) 式可知,若知道基线长度B和基线倾角α、平台飞行高度H、斜距r和系统参数(波长λ和工作模式Q),就可从绝对相位φ中解算地表高程h。
2 相位保持精度分析本节主要分析在非线性ECS自配准成像算法中引入的干涉相位误差[8]。在该成像算法中,主要采用4个近似和假设:雷达和散射体之间相对速度采用等效雷达速度近似;非线性自配准时对两天线距离差采用二次近似;非线性变标时采用二阶泰勒级数展开近似;成像处理中采用平地假设近似。这些近似和假设会引起干涉相位误差,从而造成DEM精度下降,因而有必要分析其影响。
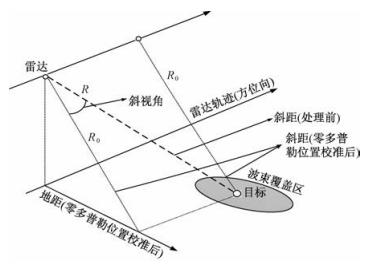
2.1 雷达和散射体之间相对速度等效误差分析雷达位置和波束在地面覆盖区的简单几何模型如图 2所示。
|
Download:
|
| 图 2 雷达位置和波束在地面覆盖区简单几何模型 Fig. 2 Simple geometry model of radar and beam on the covered ground | |
雷达轨迹指机下点在地球表面移动轨迹[9]。平台速度指平台沿飞行路径速度,用Vs表示;波束速度指零多普勒线扫过地面速度,用Vg表示。
在星载情况下,Vs就是轨道速度,可以定义在地心惯性坐标系或地心转动坐标系中,一般都假定地心转动坐标系。波束速度是在零多普勒线沿地球表面的速度。对于高度为800 km的卫星,由于轨道圆周大于轨迹圆周,因而Vg约比Vs小12%。而对于机载情况,Vs是飞机相对于地球的设计时速。因为,在机载SAR几何中,地球弯曲很小,完全可以假设Vs=Vg。在机载系统中,飞行路径局部为直线,飞机距地面一般为6 000 m,而地球半径平均为6 371.393 km,因而在飞机飞行的局部时间内,地球为局部平坦是满足的。假设下图中雷达的速度为Vr,则在局部时间内,波束指向相对于飞行方向不变,速度随着距离变化非常微小,可以忽略不计。
2.2 非线性自配准中二次近似误差分析在非线性自配准中,两天线距离差Δr′采用二次近似[8],即
| $ \Delta r' = \Delta {r_{{\rm{ref}}}} + {k_{{\rm{sl}}}}\left( {r - {r_{{\rm{ref}}}}} \right) + {k_{{\rm{s2}}}}{\left( {r - {r_{{\rm{ref}}}}} \right)^2}. $ | (2) |
在实际数据处理中,其中系数ks1和ks2为利用最小二乘近似求取。其中Δrref为参考斜距处的两天线路径差,rref为参考斜距。
不考虑平地假设误差,根据图 1两天线几何关系可得两天线距离差的精确表达式为
| $ \begin{array}{l} \Delta r = {A_2}P - {A_1}P\\ \;\;\;\;\; = \sqrt {{{\left( {H - h + B\sin \alpha } \right)}^2} + {{\left( {\left( {H - h} \right)\tan {\theta _1} - B\cos \alpha } \right)}^2}} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\left( {H - h} \right)/\cos {\theta _1}. \end{array} $ | (3) |
因此,二次近似造成的距离向两天线路径差为
| $ \begin{array}{l} \delta \Delta r = \Delta r - \Delta r'\\ \;\;\;\;\;\; = \sqrt {{{\left( {H - h + B\sin \alpha } \right)}^2} + {{\left( {\left( {H - h} \right)\tan {\theta _1} - B\cos \alpha } \right)}^2}} - \\ \;\;\;\;\;\;\;\;\;\;\;\left( {H - h} \right)/\cos {\theta _1} - \left[ {\Delta {r_{{\rm{ref}}}} + {k_{{\rm{sl}}}}\left( {r - {r_{{\rm{ref}}}}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {{k_{{\rm{s}}2}}{{\left( {r - {r_{{\rm{ref}}}}} \right)}^2}} \right], \end{array} $ | (4) |
其中: Δrref为参考斜距处两天线路径差,在计算精确值时采用式(3) 计算;θ1为参考斜距处的视角。
实际数据成像时采用Δrref≈-Bsin(θref-α),也会引入误差。因该斜距只需计算一次,可以采用式(3) 直接计算,只需要修改该式中的θ为参考斜距处的视角即可,从而消除该部分误差。
为了定量研究二次近似造成的距离向误差对配准精度及干涉相位的影响,采用表 1的典型机载参数进行仿真分析。
|
|
表 1 仿真参数 Table 1 Simulation parameters |
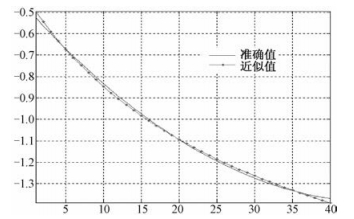
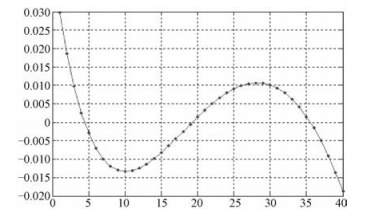
由图 3和图 4的结果可知,当采用式(2) 进行两天线斜距差近似时,会引入最大0.03 m的斜距差误差,当距离向分辨率为0.5 m时,将造成0.06个像素的失配量;绝大部分斜距差误差控制在0.013 m以内,即引起0.026个像素的失配量。这对距离向配准已经可以保持非常高的配准精度,因而这种二次近似是可以接受的。当距离向分辨率较高时,如0.1 m分辨率时,这时绝大部分的斜距差误差引起0.13个像素的失配量,超过0.1个像素的失配量,会引起相干性降低,此时不能忽略二次近似误差。因此,当系统距离向分辨率较高,一般优于0.1个像素时,要考虑距离向二次近似造成的误差。
|
Download:
|
| 图 3 精确和二次近似斜距差沿距离向变化曲线 Fig. 3 Variation curves of accurate range difference and second approximate range difference with the range | |
|
Download:
|
| 图 4 二次近似引起两天线路径差误差随距离变化图 Fig. 4 Variation curve of path difference error caused by quadratic approximation with the range | |
在非线性ECS自配准成像算法中,距离向变标时,与变标因子有关的相位因子包含三次方因子[8],如式(5) 所示。将该因式展开时,只进行二阶泰勒展开,没有考虑高阶余项的影响,这会引入一定误差,因而有必要进行分析。
| $ \begin{array}{l} \Phi = {\rm{\pi }}{K_{\rm{s}}}\left( {{f_{\rm{t}}},{r_{{\rm{ref}}}}} \right)\left[ {{{\left( {\tau - \frac{{2{R_2}\left( {{f_{\rm{t}}},{r_0}} \right)}}{c}} \right)}^2} + } \right.\\ \;\;\;\;\;\;\;\left. {{\alpha _{{\rm{scll}}}}\left( {{f_{\rm{t}}}} \right){{\left( {\tau - \frac{{2\left( {m\Delta {r_{{\rm{ref}}}} + {R_1}\left( {{f_{\rm{t}}},{r_{{\rm{ref}}}}} \right)} \right)}}{c}} \right)}^2}} \right] + \\ \;\;\;\;\;\;\;{\rm{\pi }}{K_{\rm{s}}}\left( {{f_{\rm{t}}},{r_{{\rm{ref}}}}} \right){\alpha _{{\rm{scl2}}}}\left( {{f_{\rm{t}}}} \right) \cdot \\ \;\;\;\;\;\;\;{\left( {\tau - \frac{{2\left( {m\Delta {r_{{\rm{ref}}}} + {R_1}\left( {{f_{\rm{t}}},{r_{{\rm{ref}}}}} \right)} \right)}}{c}} \right)^3}, \end{array} $ | (5) |
式中:
距离向非线性变标时,先通过变标将天线A2相位中心移到τ′0=2(r0+rrefα(ft)+mΔrref)/c,再在距离向频域将相位中心平移2 mΔrref/c后使两天线相位中心一致τ0=2(r0+rrefα(ft))/c,完成距离向自配准。
首先对式(5) 中的因子进行化简计算:
| $ \begin{array}{l} {R_2}\left( {{f_{\rm{t}}},{r_0}} \right) = {r_0}\left( {1 + \alpha \left( {{f_{\rm{t}}}} \right)} \right) + m\Delta {r_0} \approx \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{r_0}\left( {1 + \alpha \left( {{f_{\rm{t}}}} \right)} \right) + m\left[ {\Delta {r_{{\rm{ref}}}} + {k_{{\rm{s1}}}}\left( {{r_0} - } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {{r_{{\rm{ref}}}}} \right) + {k_{{\rm{s2}}}}{{\left( {{r_0} - {r_{{\rm{ref}}}}} \right)}^2}} \right], \end{array} $ | (6) |
| $ \begin{array}{l} {{\tau '}_0} - \frac{{2{R_2}\left( {{f_{\rm{t}}},{r_0}} \right)}}{c} = - \frac{2}{c}\left[ {\left( {{r_0} - {r_{{\rm{ref}}}}} \right) \cdot } \right.\\ \;\;\;\;\;\;\;\left. {\left( {\alpha \left( {{f_{\rm{t}}}} \right) + m{k_{{\rm{s1}}}}} \right) + m{k_{{\rm{s2}}}}{{\left( {{r_0} - {r_{{\rm{ref}}}}} \right)}^2}} \right], \end{array} $ | (7) |
| $ {{\tau '}_0} - \frac{{2\left( {m\Delta {r_{{\rm{ref}}}} + {R_1}\left( {{f_{\rm{t}}};{r_{{\rm{ref}}}}} \right)} \right)}}{c} = \frac{2}{c}\left[ {\left( {{r_0} - {r_{{\rm{ref}}}}} \right)} \right]. $ | (8) |
将式(5) 在τ=τ′0处进行泰勒级数展开可得
| $ \begin{array}{l} \Phi = \Phi \left( {{{\tau '}_0}} \right) + \frac{{\Phi '\left( {{{\tau '}_0}} \right)}}{{1!}}\left( {\tau - {{\tau '}_0}} \right) + \\ \;\;\;\;\;\;\frac{{\Phi ''\left( {{{\tau '}_0}} \right)}}{{2!}}{\left( {\tau - {{\tau '}_0}} \right)^2} + \\ \;\;\;\;\;\; \cdots + \frac{{{\Phi ^{\left( n \right)}}\left( {{{\tau '}_0}} \right)}}{{n!}}{\left( {\tau - {{\tau '}_0}} \right)^n} + {R_n}\left( \tau \right), \end{array} $ | (9) |
其中
推导式(9) 中各阶导数,将式(6)、式(7) 和式(8) 代入可得
| $ \begin{array}{l} \Phi \left( {{{\tau '}_0}} \right) = \frac{{4{\rm{\pi }}{K_{\rm{s}}}\left( {{f_{\rm{t}}},{r_{{\rm{ref}}}}} \right)}}{{{c^2}}}\left[ {{\alpha _{{\rm{scl1}}}}\left( {{f_{\rm{t}}}} \right){{\left( {{r_0} - {r_{{\rm{ref}}}}} \right)}^2} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {{r_0} - {r_{{\rm{ref}}}}} \right)^2}\left( {\alpha \left( {{f_{\rm{t}}}} \right) + m{k_{{\rm{s1}}}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{{\left. {m{k_{{\rm{s2}}}}\left( {{r_0} - {r_{{\rm{ref}}}}} \right)} \right)}^2}} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{8{\rm{\pi }}{K_{\rm{s}}}\left( {{f_{\rm{t}}},{r_{{\rm{ref}}}}} \right)}}{{{c^3}}}{\alpha _{{\rm{scl2}}}}\left( {{f_{\rm{t}}}} \right){\left( {{r_0} - {r_{{\rm{ref}}}}} \right)^3}, \end{array} $ | (10) |
| $ \begin{array}{l} \Phi '\left( {{{\tau '}_0}} \right) = 4{\rm{\pi }}{K_{\rm{s}}}\left( {{f_{\rm{t}}},{r_{{\rm{ref}}}}} \right)\left( {{r_0} - {r_{{\rm{ref}}}}} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\frac{{\left( {{r_0} - {r_{{\rm{ref}}}}} \right)\left( {3{\alpha _{{\rm{scl2}}}}\left( {{f_{\rm{t}}}} \right) - cm{k_{{\rm{s}}2}}} \right)}}{{{c^2}}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left[ {{\alpha _{{\rm{scl1}}}}\left( {{f_{\rm{t}}}} \right) - \left( {\alpha \left( {{f_{\rm{t}}}} \right) + m{k_{{\rm{s1}}}}} \right)} \right]} \right], \end{array} $ | (11) |
| $ \begin{array}{l} \Phi ''\left( {{{\tau '}_0}} \right) = 2{\rm{\pi }}{K_{\rm{s}}}\left( {{f_{\rm{t}}},{r_{{\rm{ref}}}}} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {{\alpha _{{\rm{scl1}}}}\left( {{f_{\rm{t}}}} \right) + 1 + \frac{{6{\alpha _{{\rm{scl2}}}}\left( {{f_{\rm{t}}}} \right)\left( {{r_0} - {r_{{\rm{ref}}}}} \right)}}{c}} \right], \end{array} $ | (12) |
| $ \Phi '''\left( {{{\tau '}_0}} \right) = 6{\rm{\pi }}{K_{\rm{s}}}\left( {{f_{\rm{t}}},{r_{{\rm{ref}}}}} \right){\alpha _{{\rm{scl2}}}}\left( {{f_t}} \right). $ | (13) |
由式(5) 可知,4阶以上导数Φ""(τ′0)=0,即最高为3阶导数,则式(9) 为
| $ \begin{array}{l} \Phi = \Phi \left( {{{\tau '}_0}} \right) + \Phi '\left( {{{\tau '}_0}} \right)\left( {\tau - {{\tau '}_0}} \right) + \\ \;\;\;\;\;\;\;\frac{{\Phi ''\left( {{{\tau '}_0}} \right)}}{2}{\left( {\tau - {{\tau '}_0}} \right)^2} + \frac{{\Phi '''\left( {{{\tau '}_0}} \right)}}{6}{\left( {\tau - {{\tau '}_0}} \right)^3}. \end{array} $ | (14) |
非线性ECS自配准成像算法中只用了2阶泰勒展开,将式(13) 代入可得泰勒级数展开近似误差为
| $ \begin{array}{l} \Delta \Phi = \frac{{\Phi '''\left( {{{\tau '}_0}} \right)}}{6}{\left( {\tau - {{\tau '}_0}} \right)^3} = {\rm{\pi }}{K_{\rm{s}}}\left( {{f_{\rm{t}}},{r_{{\rm{ref}}}}} \right) \cdot \\ \;\;\;\;\;\;\;\;\;{\alpha _{{\rm{scl2}}}}\left( {{f_t}} \right){\left( {\tau - {{\tau '}_0}} \right)^3}. \end{array} $ | (15) |
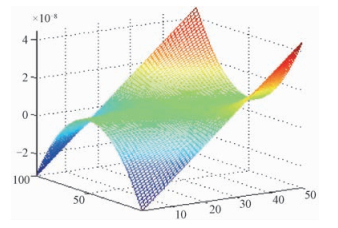
在分析式(15) 的误差时会用到Ks(ft, rref)、αscl2(ft)、τ-τ′0等参数,因而要确定各个量的范围,如式(16) 所示。其中ft为方位向频率,ks2为最小二乘拟合获取的系数。
| $ \begin{array}{l} {r_0} \in \left[ {{r_{\min }},{r_{\max }}} \right],{f_{\rm{t}}} \in \left[ {{f_{\min }},{f_{\max }}} \right],\\ {\alpha _{{\rm{scl2}}}}\left( {{f_t}} \right) = \frac{{cm}}{3}{k_{{\rm{s}}2}},\\ \tau - {{\tau '}_0} = \frac{2}{c}\left[ {\alpha \left( {{f_t}} \right)\left( {{r_0} - {r_{{\rm{ref}}}}} \right) - m\Delta {r_{{\rm{ref}}}}} \right]. \end{array} $ | (16) |

|
Download:
|
| 图 5 Ks(ft, rref)随方位向变化曲线 Fig. 5 Variation curve of Ks(ft, rref) with the azimuth | |

|
Download:
|
| 图 6 α(ft)随方位向频率变化曲线 Fig. 6 Variation curve of α(ft) with the azimuth | |
|
Download:
|
| 图 7 τ-τ′0在方位向和距离向的变化 Fig. 7 Changes in (τ-τ′0) with azimuth and range | |
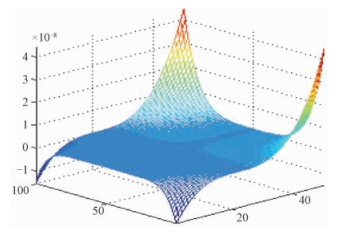
|
Download:
|
| 图 8 相位误差随方位向和距离向的变化 Fig. 8 Changes in phase error with azimuth and range | |
最小二乘拟合后ks2=4.043 7e-8,可得αscl2(ft)=4.043 7。最大相位误差4.407 0e~8 rad,最小相位误差为-1.575 0e~8 rad,化为角度最大相位误差约为2.525 1e-6°。这个误差非常小,对干涉相位影响可以忽略。因此,非线性ECS自配准成像算法中,非线性变标时可采用二阶泰勒级数展开近似。
2.4 成像中的平地假设误差分析在非线性ECS自配准成像处理中,对地球的弯曲平面进行了平地假设,没有考虑地形变化带来的影响,这将造成斜距表达式和变标因子等产生误差,下面将分析这种误差影响。
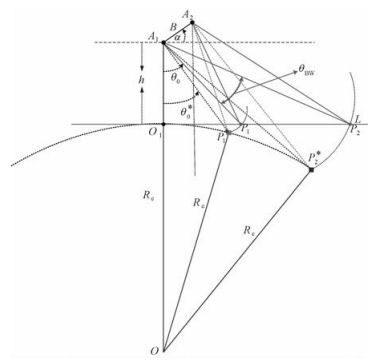
对于机载双天线InSAR系统而言,图 9给出平地近似和地球弯曲表面的几何关系示意图,该图表示的是天线A1发射信号,而天线A1和A2同时接收信号情况下的几何关系。其中A1和A2为两个天线,O1为天线A1正下方与地平面L的交点,O为地球中心,Re为地球半径,θ0为天线A1最近斜距下视角,θBW为天线A1的距离向波束宽度,P1和P2分别为最近斜距和最远斜距与地平面L的交点。而P1*和P2*分别以天线A1为圆心,以最近斜距与最远斜距为半径画圆与地球表面的交点。h为天线A1到地平面的高度,基线长度为B,基线倾角为α。
|
Download:
|
| 图 9 地球平地与地球弯曲平面几何示意图 Fig. 9 Geometry of flat and curved grounds | |
在此模型中,天线A1发出信号,两个天线都接收信号,因此,天线A1的斜距没有误差。而当以A1为圆心画圆与地球表面相交时,由于天线下视角发生变化,因而天线A2的斜距发生变化,两天线的路径差就变为天线A2平地近似的路径差。
设天线A1的斜距为R,下视角为θ,则
| $ R = h/\cos \theta , $ | (17) |
天线A2的平地近似斜距为
| $ {{\bar R}_2} = \sqrt {{B^2} + {B^2} - 2BR\sin \left( {\theta - \alpha } \right)} , $ | (18) |
设天线A1与地球表面交点对应下视角为θ*,则
| $ \begin{array}{l} {\theta ^ * } = {\mathop{\rm arc}\nolimits} \;cos\left( {\frac{{{R^2} + {{\left( {{R_{\rm{e}}} + h} \right)}^2} - R_{\rm{e}}^2}}{{2R\left( {{R_{\rm{e}}} + h} \right)}}} \right)\\ \;\;\;\; = {\mathop{\rm arc}\nolimits} \;cos\left( {\frac{{{R^2} + {h^2} + 2{R_{\rm{e}}}h}}{{2R\left( {{R_{\rm{e}}} + h} \right)}}} \right), \end{array} $ | (19) |
可得天线A2与地球表面交点对应的斜距为
| $ {R_2} = \sqrt {{B^2} + {R^2} - 2BR\sin \left( {{\theta ^ * } - \alpha } \right)} , $ | (20) |
则由于平地近似造成的天线两天线斜距误差为
| $ \begin{array}{l} \Delta {R_{12}} = {R_2} - {{\bar R}_2}\\ \;\;\;\;\;\;\;\; = \sqrt {{B^2} + {R^2} - 2BR\sin \left( {{\theta ^ * } - \alpha } \right)} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\sqrt {{B^2} + {R^2} - 2BR\sin \left( {{\theta ^ * } - \alpha } \right)} , \end{array} $ | (21) |
引起的干涉相位误差为
| $ \Delta \varphi = 2{\rm{\pi }}\Delta {R_{12}}/\lambda . $ | (22) |
为定性并更加直观地研究由于平地近似造成的误差,现利用表 1中较为典型的机载双天线InSAR系统参数进行误差仿真分析,地球平均半径Re=6 371.393 km。
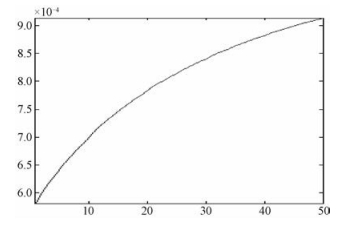
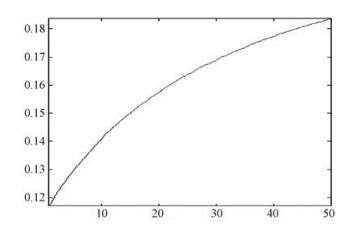
图 10和图 11为仿真结果,由该图可知,在表 1参数中,由于对地球面采用平地近似引起的两天线最大斜距误差约为9.134 071e-04 m,从而导致的最大干涉相位误差为0.183 651 rad,约为10.522 4°。采用平地近似,主要在干涉运动补偿的轨迹误差校正和相位补偿时造成误差,这个误差大小对于高精度InSAR系统(高程精度优于0.5 m时)会造成一定的影响,要在干涉运动补偿部分予以考虑。
|
Download:
|
| 图 10 ΔR12随距离向的变化情况 Fig. 10 Changes in ΔR12 with the range | |
|
Download:
|
| 图 11 Δφ随距离向的变化情况 Fig. 11 Changes in Δφ with the range | |
为进一步提高机载双天线干涉SAR系统的相位保持精度,进而提高最终的DEM产品精度,本文针对目前广泛应用的ECS自配准成像算法,分析其中4个近似误差对相位的影响,即雷达和散射体之间相对速度等效误差、非线性自配准时两天线距离差的二次近似误差、非线性变标时二阶泰勒近似误差及成像处理中平地假设误差,并得出每个因素的定性和定量相位误差。这些近似误差的分析将为高精度InSAR系统的相位精度的提升提供进一步思考和解决问题的方向。
| [1] | Chen L F, Xie W B, Huang Y F. Estimation of initial phase offset in real-time for airborne dual-antenna InSAR system [C]//Radar Conference 2013, IET International. Xi'an, 14-16 April, 2013: 1-4. |
| [2] | 陈立福, 林月冠, 彭曙蓉, 等. 一种用于机载双天线InSAR系统的实时DEM生成方法及实现[J]. 中国科学院大学学报, 2014, 31(5):678–684. |
| [3] | 杜亚男, 冯光财, 李志伟, 等. TerraSAR-X/ TanDEM-X获取高精度数字高程模型技术研究[J]. 地球物理学报, 2015, 58(9):3089–3102. DOI:10.6038/cjg20150907 |
| [4] | 孙亚飞, 江利明, 柳林, 等. TanDEM-X双站InSAR地形提取及精度评估[J]. 武汉大学学报(信息科学版), 2016, 41(1):101–105. |
| [5] | 李芳芳, 胡东辉, 丁赤飚, 等. 机载双天线InSAR对飞数据处理与分析[J]. 雷达学报, 2015, 4(1):38–48. |
| [6] | Moreira A, Mittermayer J, Scheiber R. Extended chirp scaling algorithm for air-and spaceborne SAR data processing in stripmap and scanSAR imaging modes[J]. IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(5):1123–1135. DOI:10.1109/36.536528 |
| [7] | 李绍恩, 向茂生, 吴一戎. 一种新的双天线干涉SAR自配准成像算法[J]. 电子与信息学报, 2004, 26(Suppl.):237–243. |
| [8] | 陈立福, 韦立登, 向茂生, 等. 机载双天线干涉SAR非线性近似自配准成像算法[J]. 电子与信息学报, 2010, 32(9):2208–2214. |
| [9] | Cumming I G, Wong F H. Digital processing of synthetic aperture radar data: algorithms and implementation[M]. Beijing: Electronic Industry Press, 2007. |
 2017, Vol. 34
2017, Vol. 34 


