2. 中国科学院大学, 北京 100049;
3. 安徽理工大学土木建筑学院, 安徽 淮南 232001
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. School of Civil Engineering and Architecture, Anhui University of Science & Technology, Huainan 232001, Anhui China
自由表面流的数值模拟分析是计算流体力学中最具挑战的问题之一。光滑粒子流体动力学(smoothed particle hydrodynamics, SPH)方法在处理自由表面流问题时不需要额外的方程或技术来追踪自由面的位置,并且基于拉格朗日的架构使其避免了数值耗散的出现。因此与传统的基于网格的方法相比,具有独特的优势。
光滑粒子流体动力学方法由Gingold和Monaghan[1]、Lucy[2]于1977年分别提出,最初用于求解天体物理学问题。SPH法基于拉格朗日粒子对空间计算域进行离散,这些粒子挟带有表征计算域特征的物理量,如质量、动量和速度等。场变量及其导数借助粒子和核函数以某种加权求和的方式进行计算,这种求和只涉及场变量及核函数的导数值,而不需要求解场变量本身的导数,因此降低了对场变量连续性的要求。
Shao和Lo[3]采用不可压缩SPH方法、基于Cross流变模型分析非牛顿流体在定床上的溃坝问题。Laigle等[4]基于单相的SPH方法,采用Bingham模型分析黏性泥石流与结构间的相互作用。Manenti等[5]在分析人工蓄水结构时引入Mohr-Coulomb屈服准则以及颗粒物的Shields原理,并对2个准则的敏感性进行分析。Razavitoosi等[6]分析动床溃坝问题时,将底床颗粒物视为符合Bingham流变特征的非牛顿流体,底床颗粒物在动量方程中既包括依据实验结果、由速度拟合而来的人工黏度项,又包括依据剪切率张量第二部变量确定的有效黏度项。由于缺少底床颗粒物的启动判断条件,Razavitoosi等在定义Bingham模型的有效黏度时,引入一个放大系数,以便能够反映底床颗粒物在未启动条件下具有很高的黏度,但该放大系数缺少物理解释。Ulrich等[7]在分析船舶工程问题时,基于Mohr-Coulomb屈服准则提出固液混合黏度计算公式,并提出基于土颗粒体积比的悬浮质黏度计算公式。Ran等[8]基于不可压缩光滑粒子流体动力学(ISPH)、利用Shakibaeinia和Jin[9]提出的混合黏度的计算公式分析动床溃坝问题,但该公式是基于牛顿流体特征提出的,在分析具有非牛顿特征的底床颗粒物时,其精度有限。底床颗粒物在流体冲刷下会经历由静止到启动,并有部分颗粒悬浮于水流底部等一系列状态。Fourtakas和Rogers[10]尝试将这些状态关联起来进行考虑,综合土力学中的屈服准则以及非牛顿流体力学、牛顿流体力学对动床溃坝问题进行分析。
为了更准确地描述启动后的底床颗粒物的动力学特征,本文在Fourtakas和Rogers[10]的理论框架基础上,基于颗粒流的Savage数对摩擦系数进行合理的折减。通过与已有实验数据的对比,验证了该改进公式的合理性。
1 数值模型 1.1 SPH法基本原理SPH方法以离散的、任意分布的粒子对计算域进行离散化,物理量通过相邻粒子间的插值确定。这一过程主要分两步,分别称为核近似和粒子近似。核近似是将场变量的函数及其导数以核函数及其导数的连续积分的形式进行表示;而粒子近似是将上述连续积分表示为支持域内临近离散粒子的累加求和。任意场函数f(r)基于SPH原理的一般表达形式为
| $ \left\langle {f\left( \mathit{\boldsymbol{r}} \right)} \right\rangle = \int_\Omega {f\left( {\mathit{\boldsymbol{r'}}} \right)W\left( {\mathit{\boldsymbol{r}} - \mathit{\boldsymbol{r'}},h} \right){\rm{d}}\mathit{\boldsymbol{r'}}} , $ | (1) |
其中:W称为核函数;h为光滑长度,代表核函数W的影响范围。核函数的选择需要满足归一化、紧支性和狄拉克函数性质等属性。
在方程(1) 的基础上,按照分步积分和散度定理,可以将空间位置i处的场函数及其一阶导数以离散格式表示为
| $ \left\langle {{f_i}} \right\rangle = \sum\limits_j {{f_j}{W_{ij}}{V_{ij}}} , $ | (2) |
| $ \left\langle {\nabla {f_i}} \right\rangle = \sum\limits_j {\left( {{f_j} - {f_i}} \right){\nabla _i}{W_{ij}}{V_{ij}}} , $ | (3) |
其中:mj和ρj是第j个粒子的质量和密度,而场变量fi=f(ri),核函数Wij=W(|ri-rj|, h)。
本文采用Wendland型核函数[7],形式为
| $ W = {\alpha _d}{\left( {1 - \frac{q}{2}} \right)^4}\left( {2q + 1} \right), $ | (4) |
其中: αd是归一化系数,对该核函数在二维空间中αd=7/(4πh2); q是粒子i和j之间的归一化距离,定义为q=|ri-rj|/h。
1.2 控制方程在拉格朗日框架下的弱压缩流体的控制方程[11](质量和动量守恒方程)可以写为如下形式:
| $ \frac{{{\rm{d}}\rho }}{{{\rm{d}}t}} = - \frac{1}{\rho }\frac{{\partial {v^\alpha }}}{{\partial {x^\alpha }}}, $ | (5) |
| $ \frac{{{\rm{d}}{v^\alpha }}}{{{\rm{d}}t}} = \frac{1}{\rho }\frac{{\partial {\sigma ^{\alpha \beta }}}}{{\partial {x^\beta }}} + {f^\alpha }, $ | (6) |
其中:α和β代表坐标分量,适用Einstein求和约定;vα是流体速度分量,σαβ是总应力张量的(α, β)分量;fα代表外力引起的加速度分量,一般只考虑重力;d/dt=∂/∂t+vβ·(∂/∂xβ)是物质导数。
将SPH法应用于上述2个守恒方程,可以得到守恒方程的离散格式:
| $ \frac{{{\rm{d}}{\rho _i}}}{{{\rm{d}}t}} = {\rho _i}\sum\limits_{j = 1}^N {\frac{{{m_j}}}{{{\rho _j}}}\left( {v_i^\alpha - v_j^\alpha } \right)\frac{{\partial {W_{ij}}}}{{\partial x_i^\alpha }},} $ | (7) |
| $ \frac{{{\rm{d}}v_i^\alpha }}{{{\rm{d}}t}} = \sum\limits_{j = 1}^N {{m_j}\left( {\frac{{\sigma _i^{\alpha \beta }}}{{\rho _i^2}} + \frac{{\sigma _j^{\alpha \beta }}}{{\rho _j^2}} + C_{ij}^{\alpha \beta }} \right)\frac{{\partial {W_{ij}}}}{{\partial x_i^\beta }} + g_i^\alpha } , $ | (8) |
其中:N代表支持域内粒子总数;Cijαβ是稳定项,用于减少应力波动及受拉不稳定现象,一般采用人工黏度项的形式。
总应力张量可以分解为各项同性正应力P和偏应力张量ταβ:
| $ {\mathit{\boldsymbol{\sigma }}^{\alpha \beta }} = - \mathit{\boldsymbol{P}}{\delta ^{\alpha \beta }} + {\mathit{\boldsymbol{\tau }}^{\alpha \beta }}, $ | (9) |
其中:δαβ是Kronecker delta符号,当α=β时,δαβ=1;当α≠β时,δαβ=0。将上述应力分解形式代入式(8),其中偏应力部分的计算,采用如下离散格式[12]
| $ \left\langle {\frac{1}{\rho }\frac{{\partial \tau _i^{\alpha \beta }}}{{\partial {x^\beta }}}} \right\rangle = \sum\limits_{j = 1}^N {{m_j}\left( {\frac{{\tau _i^{\alpha \beta } + \tau _j^{\alpha \beta }}}{{{\rho _i}{\rho _j}}}} \right)\frac{{\partial {W_{ij}}}}{{\partial x_{ij}^\beta }},} $ | (10) |
偏应力张量
| $ {\mathit{\boldsymbol{\tau }}^{\alpha \beta }} = 2{\mu _{{\rm{app}}}}{{\dot \varepsilon }^{\alpha \beta }}, $ | (11) |
其中,
偏应力与偏应变率之间的关系体现了流变特征,底床物质发生侵蚀后其流变特征在1.5节介绍。应变率张量可以通过速度梯度进行计算:
| $ {{\dot \varepsilon }^{\alpha \beta }} = \frac{1}{2}\left( {\frac{{\partial {v^\alpha }}}{{\partial {x^\beta }}} + \frac{{\partial {v^\beta }}}{{\partial {x^\alpha }}}} \right) - \frac{1}{3}\left( {\frac{{\partial {v^\gamma }}}{{\partial {x^\gamma }}}} \right){\delta ^{\alpha \beta }}, $ | (12) |
其中,vα是速度分量,其梯度的计算由SPH的离散格式表示为
| $ \frac{{\partial {v^\alpha }}}{{\partial {x^\beta }}}\left| {_i} \right. = \sum\limits_{j = 1}^N {\frac{{{m_j}}}{{{\rho _j}}}v_{ij}^\alpha \frac{{\partial {W_{ij}}}}{{\partial x_i^\beta }}.} $ | (13) |
在本文中,将流体看作弱可压缩流体(密度变化小于1%)。在弱可压缩SPH算法中,发生运动的颗粒物质所受压力P通过热动力学状态方程显式地计算,本文采用Tait型状态方程[13]:
| $ {P_i} = \frac{{{c^2}{\rho _0}}}{\gamma }\left( {{{\left( {\frac{{{\rho _i}}}{{{\rho _0}}}} \right)}^\gamma } - 1} \right), $ | (14) |
其中:c是声速;ρ0是参考密度;γ=7。该状态方程已在黏性流体的分析中得到应用并获得了比较理想的计算结果[14-15]。
为了保证密度的浮动范围在1%以内,声速的取值一般取流体可能出现的最大速度的10倍以上,即
| $ c > 10\max \left( {\left| \mathit{\boldsymbol{v}} \right|} \right). $ | (15) |
对未发生屈服而处于静止状态的底床颗粒物,其正应力由静止土压和孔隙水压力确定,
| $ P' = P - {P_{\rm{w}}} = \left( {{\gamma _{\rm{s}}} - {\gamma _{\rm{w}}}} \right){z_{\rm{s}}}, $ | (16) |
其中:P是静止土压;Pw是孔隙水压力;γs和γw分别是底床颗粒物和水的容重;zs是粒子到底床侵蚀界面的距离。
1.4 侵蚀起动条件底床颗粒物由于受重力和相互间的摩擦力、黏聚力作用,具有一定的抗冲刷能力。只有来流满足一定条件时,底床颗粒物才会起动并被来流挟带走。
Fourtakas和Rogers[12]对比分析Mohr-Coulomb和Drucker-Prager两种侵蚀启动条件,发现由前者得到的发生侵蚀的底床颗粒层等效黏度偏大,因此侵蚀层厚度比实验结果小。因此本文假设底床颗粒物质满足Drucker-Prager准则,其应变率张量可以分解为弹性部分和塑性部分,而后者可以依据塑性流动准则进行计算:
| $ {{\dot \varepsilon }^p} = \dot \lambda \frac{{\partial {g_{\rm{p}}}}}{{\partial \sigma }}, $ | (17) |
其中:
只有当应力达到屈服面时才发生侵蚀启动。屈服面的形状由Drucker-Prager屈服准则描述,表示为
| $ f = {\alpha _\phi }{I_1} + \sqrt {{J_2}} - {k_c} = 0, $ | (18) |
其中:I1是第一应力不变量,即I1=σγγ/3;J2是偏应力张量的第二不变量,即J2=ταβταβ/2。
各向同性物质在处于屈服临界状态时,流体应力与底床颗粒物的屈服强度平衡,即
| $ \left| {{\tau _y}} \right| = - {\alpha _\phi }{I_1} = {\kappa _c}. $ | (19) |
因此,认为当满足(20) 式时,水动力达到底床颗粒物的屈服强度,底床颗粒物在侵蚀作用下发生启动,
| $ \sqrt {{J_2}} \ge - {\alpha _\phi }{p_{\rm{s}}} + {\kappa _c}, $ | (20) |
其中:Ps是颗粒物所受的有效压应力;αϕ和κc是Drucker-Prager准则中的常数,可以由摩尔库仑准则的黏聚力c和内摩擦角ϕ算得[16]:
| $ {\alpha _\phi } = \frac{{\tan \phi }}{{\sqrt {9 + 12{{\tan }^2}\phi } }},{\kappa _c} = \frac{{3c}}{{\sqrt {9 + 12{{\tan }^2}\phi } }}. $ | (21) |
由式(19) 以及
| $ {\mu _{{\rm{app}}}} = \frac{{ - {\alpha _\phi }{p_{\rm{s}}} + {\kappa _c}}}{{2\sqrt {I{I_D}} }}. $ | (22) |
部分底床颗粒物受溃决水体冲刷而启动,与水发生混合并在其下的静止底床颗粒物上发生运动,其流变特征可以用黏塑性流变模型进行描述。在常用的流变模型中,Bingham模型[17]是最简单的一种,该模型体现了物质在屈服之后,其偏应变与所受剪切应力之间的线性关系。而Herschel-Bulkley模型则能够描述黏塑性物质在塑性阶段的多种非线性变形特征,更具有广泛性。Herschel-Bulkley流变模型[4]可以表示为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\tau }} = \left( {\frac{{\left| {{\mathit{\boldsymbol{\tau }}_y}} \right|}}{{\sqrt {I{I_D}} }} + K{{\left( {\sqrt {I{I_D}} } \right)}^{\frac{{n - 1}}{2}}}} \right)\mathit{\boldsymbol{D}},\;\;\;\;\;\;\left| \mathit{\boldsymbol{\tau }} \right| > {\mathit{\boldsymbol{\tau }}_y},\\ \mathit{\boldsymbol{D}} = 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| \mathit{\boldsymbol{\tau }} \right| \le {\mathit{\boldsymbol{\tau }}_y}, \end{array} \right. $ | (23) |
其中:τy代表屈服应力;IID是偏应变张量的第二不变量;K是稠度指数。
Bingham模型和Herschel-Bulkley模型在屈服应力附近都存在应力的转折点,Frigaard和Nouar[18]对黏塑性非牛顿流变模型进行综合分析后认为Herschel-Bulkley-Papanastasiou(HBP)模型[19]以连续函数的形式提供对Herschel-Bulkley模型最好的近似。Herschel-Bulkley-Papanastasiou模型的等效黏度表示为
| $ {\mu _{\rm{s}}} = \frac{{\left| {{\mathit{\boldsymbol{\tau }}_y}} \right|}}{{\sqrt {I{I_D}} }}\left( {1 - {{\rm{e}}^{ - m\sqrt {I{I_D}} }}} \right) + K{\left( {\sqrt {I{I_D}} } \right)^{n - 1}}, $ | (24) |
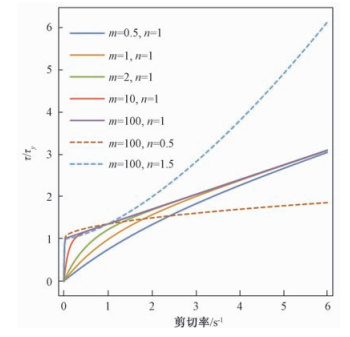
其中:m控制着HBP模型与Herschel-Bulkley模型在塑性屈服过渡段(图 1中曲线的转折点附近)的接近程度,m越大则HBP模型越接近Herschel-Bulkley模型。参数n控制着物质在剪应力作用下的应变硬化(或软化)特征;n>1发生应力硬化,n<1发生应力软化;n=1时,HBP模型则简化为Bingham模型。τy代表屈服应力。偏应变张量的第二不变量IID定义为
| $ I{I_D} = \frac{1}{2}\left[ {{{\left( {\frac{{\partial {u^\alpha }}}{{\partial {x^\alpha }}}} \right)}^2} + {{\left( {\frac{{\partial {u^\beta }}}{{\partial {x^\beta }}}} \right)}^2} + \frac{1}{2}\left( {\frac{{\partial {u^\alpha }}}{{\partial {x^\beta }}} + \frac{{\partial {u^\beta }}}{{\partial {x^\alpha }}}} \right)}^2 \right]. $ | (25) |
|
Download:
|
| 图 1 HBP模型示意图 Fig. 1 Schematic diagram of HBP model | |
从数值计算的角度来说,SPH法是基于显式时间迭代算法的,时间步的上限是基于一定的收敛准则确定的。Bingham模型和Herschel-Bulkley模型在分母中都包含偏应变张量第二不变量IID,当IID趋于无穷小时,等效黏度会趋于无穷大,物理上代表未屈服区域内底床颗粒物不发生变形,但是在数值计算上会导致计算收敛困难。因此可以为上述两种模型的等效黏度设置一个上限值,通常取K的1 000倍比较合理。HBP模型中包含IID的指数项
底床颗粒物满足侵蚀启动条件而发生运动后,可以将其看作一种伪流体,基于黏塑性流变模型来描述其运移变形特征。发生运动的底床颗粒物与溃决水体接触面附近,颗粒物受冲刷及水的浮力作用会悬浮于水流底部,进而导致这底部水流的黏度有所提高,提高后的黏度直接影响两相界面的动力学特征,对计算结果有重要影响。Gotoh和Fredso[20]在采用移动粒子半隐式(MPS)法分析细颗粒在水中的沉降时,采用如下公式计算混合黏度:
| $ {\mu _{{\mathop{\rm mix}\nolimits} }} = {\mu _{\rm{w}}}/{\left( {1 + {\alpha _{\rm{s}}}\frac{{{\rho _{\rm{s}}}}}{{{\rho _{\rm{w}}}}}} \right)^{1/2}}, $ | (26) |
其中:ρs和ρw分别是颗粒物和水的密度;αs是固体颗粒物的体积比。Shakibaeinia和Jin[9]也采用同样的公式。Fourtakas[10]在分析动床条件下的溃坝问题时,将含悬浮颗粒的水流视为牛顿流体,认为混合黏度是固体颗粒物的体积比的函数,采用Vand模型[21]来计算混合黏度:
| $ {\mu _{{\mathop{\rm mix}\nolimits} }} = {\mu _{\rm{w}}}{{\rm{e}}^{\frac{{2.5{\alpha _{\rm{s}}}}}{{1 - 39{\alpha _{\rm{s}}}/64}}}},\left( {{\alpha _{\rm{s}}} \le 0.3} \right), $ | (27) |
其中,αs采用如下离散格式计算:
| $ {\alpha _{{\rm{s,}}i}} = \sum\limits_{{j_{{\rm{sat}}}} \in 2h}^N {\frac{{{m_j}}}{{{\rho _j}}}} /\sum\limits_{j \in 2h}^N {\frac{{{m_j}}}{{{\rho _j}}}} , $ | (28) |
式中:jsat是i粒子的支持域内处于饱和状态的粒子;h是光滑半径。
通过式(27) 计算的混合黏度,虽然体现了固相体积比对混合黏度的影响,但计算是基于液相的黏度μw进行计算的,实际是将固液混合体看作伪牛顿流体,因此该公式仅当细颗粒物含量较小时才适用。
1.7 流变模型的改进Bagnold耗散压力原理认为,牛顿流体中的颗粒流在剪切应力作用下所产生的能量耗散是颗粒间的非弹性碰撞产生的,其大小依赖于颗粒间的回弹系数[22]。Armanini通过对实验的分析发现,当水下颗粒流内存在明显摩擦应力时,摩擦产生的剪应力既依赖剪切率同时也依赖压力(库仑型),其摩擦角不应该是常数,而是依赖于流体的局部运动特征,如颗粒间的压应力、接触特征以及颗粒的物质构成等因素[23]。体现上述主要因素对颗粒流剪切应力影响的参数称为Savage数[24],表示为
| $ {I_{\rm{s}}} = \frac{{{\rho _{\rm{s}}}{{\left( {\dot \gamma {d_{\rm{p}}}} \right)}^2}}}{{{p^g}}}, $ | (29) |
其中:ρs是颗粒密度;
摩擦产生的剪切应力在趋近静止底床表面时应该符合库仑型摩擦特征;当Is足够大时,应逐渐趋于消失[23]。如果将水下颗粒流内的摩擦系数看作常数,则不能充分反映真实的动力学特征,必然导致计算结果有一定的出入。
以底床颗粒物的摩擦特征为基础,本文对启动后的水下颗粒流内摩擦应力部分进行修正,提出如下混合黏度计算公式:
| $ {\mu _{{\mathop{\rm mix}\nolimits} }} = \frac{{{I_{{\rm{so}}}}}}{{{I_{\rm{s}}} + {I_{{\rm{so}}}}}}\frac{{\left| {{\mathit{\boldsymbol{\tau }}_y}} \right|}}{{\sqrt {I{I_D}} }}\left( {1 - {{\rm{e}}^{ - m\sqrt {I{I_D}} }}} \right) + K{\left( {\sqrt {I{I_D}} } \right)^{n - 1}}, $ | (30) |
其中,Iso是依赖间隙流体特征和固体颗粒物构成特征的参数,其值需要通过实验确定。Is是Savage数,由式(29) 计算。由于Is越靠近底床数值越小,因此由式(30) 确定的混合黏度μmix在静止底床的上边界处取得最大值。
2 溃坝问题分析采用Spinewine[25]的溃坝室内试验数据对上述模型进行验证。
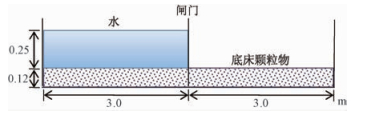
2.1 模型及相关参数Spinewine所做实验的几何模型如图 2所示,模型总长度为6.0 m,宽度为0.25 m。模型底部全长范围内平铺0.12 m厚的松散PVC细颗粒(等效直径dp=3.9 mm),闸门位于3.0 m处,闸门左侧水体高度为0.25 m。
|
Download:
|
| 图 2 计算模型示意图 Fig. 2 Geometry of numerical modeling model | |
底床PVC颗粒物处于饱和状态,颗粒密度为1 580 kg/m3,初始体积比为0.58,因此换算为等效均质体后的等效体积密度为1 336 kg/m3。颗粒物内摩擦角为38°,黏聚力忽略不计。
数值模拟基于开源的SPHYSICS2D代码,结合本文介绍的模型在该代码基础上进行二次开发,使其能够计算动床条件下的冲刷侵蚀问题。本文所涉及的溃坝问题的几何模型相对比较简单、规则,可以利用SPHYSICSgen2D完成建模。
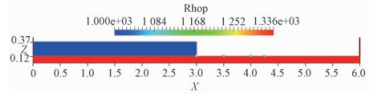
根据上述几何尺寸建立数值计算模型,初始时刻的数值计算模型如图 3所示,图中同时还显示了两种物质的密度(Rhop)的取值情况。
|
Download:
|
| 图 3 数值模型几何尺寸图 Fig. 3 Geometry diagram of numerical model | |
闸门后的水体最初处于静止状态,在t=0时刻打开闸门,闸门后水体发生溃决,进而对底床产生冲刷。
2.2 模拟参数基于SPH方法的模拟采用Wendland型核函数、固定的光滑半径、显式欧拉时间积分。通过虚粒子模拟固墙边界,固墙边界上应满足无滑移条件。水体和底床颗粒物初始压力按静水压力考虑。粒子间距0.005 m,光滑长度取粒子间距的1.3倍,初始时间步长1.0×10-8,CFL=0.1。采用Symplectic型[26]时间积分算法;密度过滤采用δ-SPH算法[27],密度校正系数ξ=0.1。底床颗粒物HBP模型流变模型参数n=1.8,m=100,稠度指数K=0.002。通过对实验中底床颗粒速度分布特征的拟合,确定参数Iso取值0.04。
2.3 模拟结果及对比分析 2.3.1 常摩擦系数情况当固相体积比αs≤0.3时,悬浮层内的混合黏度按式(27) 计算;悬浮层与静止底床之间的混合层(αs>0.3) 的混合黏度按式(24) 计算。
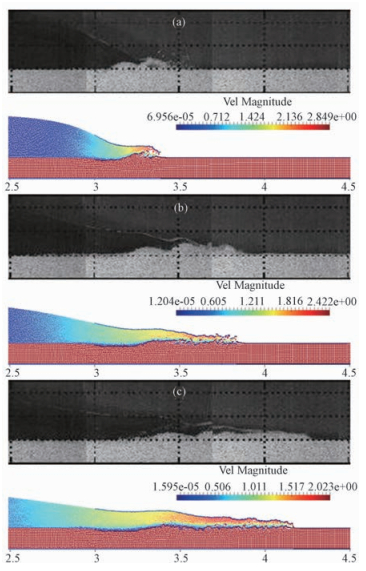
模拟总时长1 s,截取数值模拟获得的溃决水体在t=0.25、0.5和0.75 s这3个时刻的速度云图,并与实验实测结果[16]进行对比如图 4所示。
|
Download:
|
| 图 4 模拟流动形态与实验对比图 Fig. 4 Comparison of flow profiles between numerical modeling and experiment | |
从图 4(a)和(b)中可以看出,数值模拟的运动前缘与实验结果吻合的都比较好。图 4(c)是t=0.75 s时的情况,模拟的运动前缘位置比实验结果靠后。该模拟结果与Fourtakas[10]模拟Ulrich的溃坝实验[7]结论是一致的,即模型在预测侵蚀界面方面可以获得较满意的结果,但是从0.75 s开始,算得的溃决体的运动略滞后于实验结果。
2.3.2 变摩擦系数情况坝后水体溃决之后,与底床颗粒物迅速产生接触,底床颗粒物在动水压力作用下一部分颗粒上浮进入水体内部,接触边界附近的颗粒发生重新排列,颗粒间的接触紧密度发生变化。上层流体产生的快速剪切导致表层颗粒间出现碰撞应力,这些因素都导致等效摩擦系数在深度方向上的分布是不均匀的。正如在前面1.7节讨论的那样,Savage数综合反映了上述多个因素对摩擦剪切应力的影响。
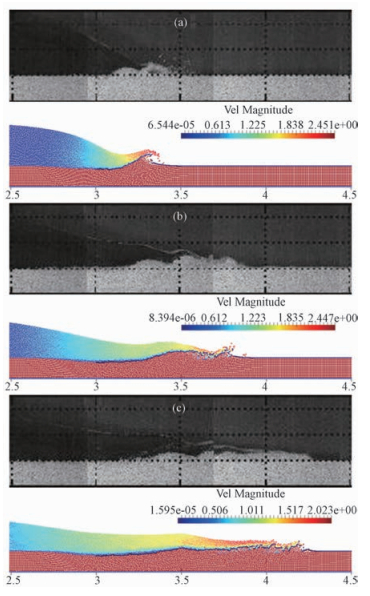
为改进数值模拟结果,当αs>0.3时,混合黏度按改进公式(30) 计算,其他参数取值与之前的模拟一样。分析1 s时间内溃决水体与底床的动态演变过程,截取t=0.25、0.5和0.75 s这3个时刻的模拟结果与实验结果进行对比,如图 5所示。
|
Download:
|
| 图 5 模拟流动形态与实验对比图(改进模型) Fig. 5 Comparison of flow profiles between numerical modeling (using an improved model) and experiment | |
将图 4与图 5进行对比可以发现,后图中数值模拟获得的上浮于原底床顶面以上的颗粒物更多,底床被冲蚀后的轮廓更接近实验结果。尽管2个模拟在αs≤0.3的悬浮质采用了相同的公式,但超过原底床顶面以上的、被冲蚀起来的颗粒有相当大的比例是满足αs>0.3的颗粒,由于针对这部分颗粒2个模拟采用的公式不同,所以结算结果会有差异。
从图 5中可以看到,数值模拟结果不仅在t=0.25 s和t=0.5 s与实验结果吻合较好,而且在t=0.75 s也具有很高的吻合度,底床颗粒物运动前缘与实验结果非常接近。
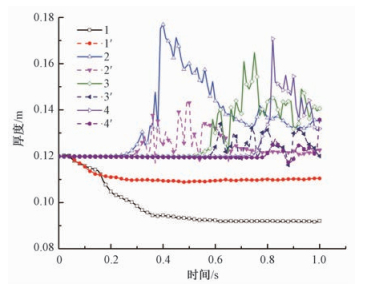
在两次数值模拟中同时记录了底床顶面4个点的底床厚度随时间变化情况。这4个点的位置如图 3所示,距离模型最左侧0点的距离分别是3.0、3.5、4.0和4.25 m。图 6中第n曲线表示采用可变摩擦系数模拟得到的第n个点处的层厚变化,第n’曲线表示采用常摩擦系数模拟得到的第n个点处的层厚变化(n=1~4)。以2和2’两条曲线为例,在x=3.5 m的第2点处,采用可变摩擦系数时发生冲蚀的时间提前了约0.04 s,冲蚀引起的最大层厚增加了33.9 mm。
|
Download:
|
| 图 6 底床高度对比图 Fig. 6 Comparison of flow depths of sediment | |
流体与固体颗粒的混合物具有非常复杂的动力学特征,受固液两相构成比例、两相各自的力学特征以及两相之间的相互作用等多种因素影响。因此,溃决流体对底床颗粒物产生高速的冲刷和侵蚀作用,这一过程伴随着复杂的动力学过程。对动床条件下溃坝问题的数值模拟既要克服数值计算方法方面的困难,同时要深入物理过程本身的机理,只有充分体现内部的物理原理,才能获得更好的仿真模拟结果。
本文以Drucker-Prager屈服准则作为侵蚀是否发生的判断条件,将发生侵蚀的颗粒以满足Herschel-Bulkley-Papanastasiou流变特征的非牛顿流体特征进行描述,较好地解决了无黏颗粒物底床是否发生侵蚀以及侵蚀后底床颗粒物的运动特征如何描述这两个关键问题。根据Armanini[23]对水中颗粒流的研究成果,考虑影响摩擦系数的主要因素,本文提出一种摩擦系数的修正公式,引入到基于SPH方法的计算模型中,通过数值模拟结果与实验结果的对比,证明了该修正公式的合理性。
通过对比分析发现,底层颗粒物摩擦系数的取值对底床的侵蚀深度分布有明显的影响。通过对HPB模型中的摩擦系数进行合理的折减,计算得到的溃决流体的流速更快,闸门附近的侵蚀量略有增加,流体运动前缘附近的颗粒上浮、雍高量将有所增加,流体运动前缘的位置与实验结果更加吻合。
在本文中以固相体积比0.3作为分界来区分启动的底床颗粒物中发生悬浮的颗粒,并且两部分采用了不同的计算模型。如何基于颗粒物本身的动力学特征来确定它们的运动形态,并以一个统一的模型来描述启动的颗粒物,需要基于对颗粒物与流体相互作用过程的更深入的分析,值得进一步深入研究。
| [1] | Gingold R A, Monaghan J J. Smoothed particle hydrodynamics:theory and application to non-spherical stars[J]. Monthly Notices of the Royal Astronomical Society, 1977, 181(3):375–389. DOI:10.1093/mnras/181.3.375 |
| [2] | Lucy L B. A numerical approach to the testing of the fission hypothesis[J]. The Astronomical Journal, 1977, 82:1013–1024. DOI:10.1086/112164 |
| [3] | Shao S, Lo E Y M. Incompressible SPH method for simulating Newtonian and non-Newtonian flows with a free surface[J]. Advances in Water Resources, 2003, 26(7):787–800. DOI:10.1016/S0309-1708(03)00030-7 |
| [4] | Laigle D, Lachamp P, Naaim M. SPH-based numerical investigation of mudflow and other complex fluid flow interactions with structures[J]. Computational Geosciences, 2007, 11(4):297–306. DOI:10.1007/s10596-007-9053-y |
| [5] | Manenti S, Sibilla S, Gallati M, et al. SPH Simulation of Sediment Flushing Induced by a Rapid Water Flow[J]. Journal of Hydraulic Engineering, 2012, 138(3):272–284. DOI:10.1061/(ASCE)HY.1943-7900.0000516 |
| [6] | Razavitoosi S L, Ayyoubzadeh S A, Valizadeh A. Two-phase SPH modelling of waves caused by dam break over a movable bed[J]. International Journal of Sediment Research, 2014, 29(3):344–356. DOI:10.1016/S1001-6279(14)60049-4 |
| [7] | Ulrich C, Leonardi M, Rung T. Multi-physics SPH simulation of complex marine-engineering hydrodynamic problems[J]. Ocean Engineering, 2013, 64:109–121. DOI:10.1016/j.oceaneng.2013.02.007 |
| [8] | Ran Q, Tong J, Shao S, et al. Incompressible SPH scour model for movable bed dam break flows[J]. Advances in Water Resources, 2015, 82(8):39–50. |
| [9] | Shakibaeinia A, Jin Y-C. A mesh-free particle model for simulation of mobile-bed dam break[J]. Advances in Water Resources, 2011, 34(6):794–807. DOI:10.1016/j.advwatres.2011.04.011 |
| [10] | Fourtakas G, Rogers B D. Modelling multi-phase liquid-sediment scour and resuspension induced by rapid flows using Smoothed Particle Hydrodynamics (SPH) accelerated with a Graphics Processing Unit (GPU)[J]. Advances in Water Resources, 2016, 92(6):186–199. |
| [11] | Xu X, Ouyang J, Yang B, et al. SPH simulations of three-dimensional non-Newtonian free surface flows[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 256(4):101–116. |
| [12] | Fourtakas G, Rogers B D, Laurence D R. Modelling sediment resuspension in industrial tanks using SPH[J]. La Houille Blanche, 2013(2):39–45. DOI:10.1051/lhb/2013014 |
| [13] | Monaghan J J. Simulating free surface flows with SPH[J]. Journal of Computational Physics, 1994, 110(2):399–406. DOI:10.1006/jcph.1994.1034 |
| [14] | Morris J, Monaghan J. A switch to reduce SPH viscosity[J]. Journal of Computational Physics, 1997, 136(1):41–50. DOI:10.1006/jcph.1997.5690 |
| [15] | Fang J, Parriaux A, Rentschler M, et al. Improved SPH methods for simulating free surface flows of viscous fluids[J]. Applied Numerical Mathematics, 2009, 59(2):251–271. DOI:10.1016/j.apnum.2008.02.003 |
| [16] | Chen W-F, Mizuno E. Nonlinear analysis in soil mechanics[M]. Amsterdam: Elsevier, 1990. |
| [17] | Rodriguez-Paz M X, Bonet J. A corrected smooth particle hydrodynamics method for the simulation of debris flows[J]. Numerical Methods for Partial Differential Equations, 2004, 20(1):140–163. DOI:10.1002/(ISSN)1098-2426 |
| [18] | Frigaard I A, Nouar C. On the usage of viscosity regularisation methods for visco-plastic fluid flow computation[J]. Journal of Non-Newtonian Fluid Mechanics, 2005, 127(127):1–26. |
| [19] | Papanastasiou T C. Flows of Materials with Yield[J]. Journal of Rheology, 1987, 31(5):385–404. DOI:10.1122/1.549926 |
| [20] | Gotoh H, Fredsoe Jr. Lagrangian two-phase flow model of the settling behavior of fine sediment dumped into water [C]//International Conference on Coastal Engineering, 2001:3906-3919. |
| [21] | Vand V. Viscosity of Solutions and Suspensions. I. Theory[J]. The Journal of Physical and Colloid Chemistry, 1948, 52(2):277–299. DOI:10.1021/j150458a001 |
| [22] | Bagnold R A. Experiments on a Gravity-Free Dispersion of Large Solid Spheres in a Newtonian Fluid under Shear[J]. Proceedings of the Royal Society of London Series A Mathematical and Physical Sciences, 1954, 225(1160):49–63. DOI:10.1098/rspa.1954.0186 |
| [23] | Armanini A, Larcher M, Nucci E, et al. Submerged granular channel flows driven by gravity[J]. Advances in Water Resources, 2014, 63(2):1–10. |
| [24] | Savage S B. The mechanics of rapid granular flows[J]. Advances in Applied Mechanics, 1984, 24(87):289–366. |
| [25] | Spinewine B. Two-layer flow behaviour and the effects of granular dilatancy in dam-break induced sheet-flow. [D] Belgium:Université catholique de Louvain PhD Thesis, 2005. https://dial.uclouvain.be/pr/boreal/object/boreal:4999?site_name=UCL |
| [26] | Leimkuhler B J, Reich S, Skeel R D. Mathematical approaches to biomolecular structure and dynamics[M]. New York: Springer, 1996: 161-185. |
| [27] | Molteni D, Colagrossi A. A simple procedure to improve the pressure evaluation in hydrodynamic context using the SPH[J]. Computer Physics Communications, 2009, 180(6):861–872. DOI:10.1016/j.cpc.2008.12.004 |
 2017, Vol. 34
2017, Vol. 34 


