2. 中国科学院大学地球科学学院, 北京 100049
2. College of Earth Sciences, University of Chinese Academy of Sciences, Beijing 100049, China
岩石等孔隙材料与介质的吸水现象普遍存在于自然界与人为工程中,吸水过程可对地下岩体稳定性[1]、建筑材料耐久性[2-3]、油气工程开采率[4-5]等产生重要影响,因此吸水特性的研究受到地下工程、建筑材料、土木工程、石油工程等多领域的关注与重视[6]。深入了解与掌握孔隙介质的吸水机理及动力学特性是从根本上解决不同领域岩石吸水问题的关键,也是将吸水特性为工程开发所用的前提。
通常认为,水在岩石等介质中的迁移方式主要有毛细过程、扩散过程及在压力梯度下的渗透这3类,而对于非饱和介质,毛细作用下的水分传输过程则占据主导[7-8]。Washburn[9]首先从多孔介质的角度提出岩石吸水动力特性的理论模型。假设岩石介质由一束平行且直径相同的毛细管组成,若不考虑重力影响,液体吸入前缘的速率取决于毛细管力,则吸入高度随时间的变化关系[9]可表示为:
| $ h\left( t \right) = \sqrt {\frac{{r\sigma \cos \theta }}{{2\eta }}t}, $ | (1) |
式中:r为毛细圆柱管半径;σ为水的表面张力;θ为接触角;η为水的黏度。该公式是岩石吸水过程理论分析及实验研究的基础,此后,Fries和Dreyer[10]、Kim和Whitesides[11]、Cai等[12]从重力作用、毛管形状、分形特征等方面对该模型进行改进和拓展。
同时,一些学者也通过室内实验研究岩石毛细吸水的动力学特性,分析不同因素对岩石吸水过程及水分分布的影响。称重法由于简便、适用性强的特点,成为应用最为广泛的实验方法,其原理是通过测量一定时间间隔内样品累计质量的变化值,计算吸水率,从而分析介质的吸水能力。李科等[13]采用一维单面吸水方式,运用称重法研究石膏质岩的吸水特性,并对比干湿循环前后吸水曲线,发现循环后岩石孔隙率变大,吸水量增加;任凯等[14]通过称重法针对渝东南下志留龙马溪组页岩开展自发渗吸实验,分析页岩层理、氯化钾溶液和阳离子表面活性剂对自吸速率和能力的影响,并提出一种基于自吸速率预测页岩储层压裂液返排率的方法;贾志刚等[15]对传统称重法进行改进,实现连续、精确测量,并分析吸水边界对吸水过程的影响。然而,称重法无法获取水分空间分布,若对样品进行切割也易造成误差并丢失大量信息。
为确定多孔介质内部水分分布规律,电阻率成像法、计算机断层扫描法、核磁共振法等逐步被应用于吸水特性的研究。查甫生等[16]通过监测土样吸水膨胀过程的电阻率参数指标变化规律,建立描述膨胀土微结构变化的电阻率评价方法;Roels和Carmeliet[17]利用X射线照相技术获得多孔介质吸水过程的二维照片,分析其含水率变化;Hanzic和Ilic[18]在实验中采用中子射线照相技术测量试件内的水分分布规律,得到x-t1/2关系曲线;蒙冕模等[19]采用低场核磁共振技术监测蒸馏水在页岩自发渗吸过程中的分布特征,发现页岩渗吸过程液体首先充满大孔隙和裂缝,且会产生大量微裂缝。但电阻率成像法对岩石样品的测试精度与适用性受限,CT法的精度与样品尺寸成反比,受非均质影响大且价格昂贵,而核磁共振技术由于其方法原理与特点,在岩石吸水动力学研究中展现出一定的技术优势。
以上方法多被用于砂岩的流体驱替、软化机理等方面的研究,如Holmes和Packer[20]和周莉等[21]利用核磁脉冲磁场梯度测定枫丹白露砂岩的水油两相运移规律,并取得一定的成果,但对砂岩自然吸水过程研究较少。本文将具有参数可控特点的人工砂岩作为研究对象,用来重现自然界岩石本身的性质以及所反映的力学和其他物理性质[22]。此外,实验将称重法与核磁共振谱分析、成像分析相结合,深入研究砂岩孔隙结构对于吸水过程的影响及机理,获取水分分布与运移信息。核磁共振的测试精度一定程度上受信噪比影响,而氢原子核磁旋比大,所产生核磁信号较强,因此该技术非常适用于监测水分的迁移过程,并且具有直观、无损、快速、适用性广等特点,在岩石吸水的相关研究中极具前景。但目前应用的核磁共振方法主要通过谱分析获得岩石吸水量与孔隙水分分布信息,对于水分迁移过程的直观监测研究较少,限制了对其动力学特性的深入研究与规律总结。本文选取不同渗透率的人工砂岩,采用称重法与核磁共振谱分析法进行对比验证,并借助核磁共振一维剖面成像技术,开展砂岩的一维垂向与三维吸水实验,研究砂岩中水分分布变化与迁移规律,并针对渗透率、吸水边界等因素对吸水过程的影响进行探讨。
1 核磁共振原理及方法介绍 1.1 核磁共振原理核磁共振(nuclear magnetic resonance,NMR)是具有自旋特性的原子核所特有的物理现象[23]。若叠加一射频场B1,且该射频场的频率与特定原子核的拉莫频率一致,核自旋系统发生共振吸收、能级跃迁的现象即为核磁共振。而射频场作用结束后,核自旋从高能级的非平衡状态恢复到低能级平衡状态的过程称为弛豫[24],根据弛豫机理的区别,将其分为纵向弛豫与横向弛豫。多孔介质中,主要通过对受限流体的横向弛豫时间(T2)进行反演来表征其孔隙结构,通常尺寸越小的空隙其横向弛豫时间越短。
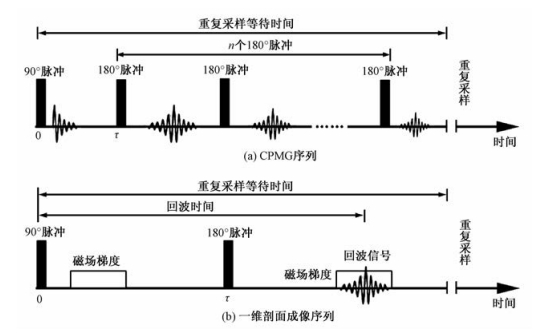
1.2 核磁共振测试方法 1.2.1 横向弛豫时间测试进行横向弛豫时间T2测量时,需要消除磁场不均匀性带来的影响,通常采用CPMG(Carr-Purcell-Meiboom-Gill)序列(脉冲时序如图 1(a)所示),通过施加多个180°射频脉冲,延缓由于磁场不均匀而导致的信号衰减,消除干扰[25]。由于多孔介质一般由不同尺寸的孔隙组成,CPMG序列测得的总弛豫M(t)是不同孔隙弛豫的叠加:
| $ M\left( t \right) = \sum\limits_i {{A_i}\exp \left( {\frac{{-t}}{{{t_{2i}}}}} \right), } $ | (2) |
|
Download:
|
| 图 1 核磁共振测试序列图 Fig. 1 Sequences of NMR measurement used in this study | |
式中:Ai为第i组分所占的比例;t2i为第i组分的弛豫时间。
通过T2谱分析,可以获得样品中水分含量变化与不同孔径孔隙中的水分分布情况,从而分析岩石的吸水能力以及孔隙结构对吸水过程的影响。
1.2.2 一维剖面成像测试为获得样品中不同位置剖面的水分含量信息,研究实现了一维核磁共振成像技术,并将其用于水分迁移规律的分析。一维剖面成像序列(如图 1(b)所示)是在90°射频脉冲间隔τ时间后加以180°射频脉冲,并在180°射频脉冲前后施加磁场梯度脉冲,利用梯度磁场进行剖面定位,根据不同剖面的首点信号强度衡量含水量。通过傅里叶变换,信号强度[26]可表示如下
| $ A = {A_0}\left[{1-\exp \left( {\frac{{-{T_{\rm{R}}}}}{{{T_1}}}} \right)} \right]\exp \left( {\frac{{ -{t_{\rm{E}}}}}{{{T_2}}}} \right), $ | (3) |
借助一维剖面成像技术,可在同一时刻获取样品区内512个不同剖面的水分含量信息,实现对于水分时空变化的分析以及毛细上升前缘的追踪。
2 实验过程与结果分析 2.1 实验过程本文实验皆在中国科学院页岩气与地质工程重点实验室开展。
2.1.1 仪器与样品核磁共振测试采用上海纽迈公司的MesoMR柜式核磁共振成像仪,磁场强度≥0.5 T,共振频率21~24 MHz,用于T2谱分析和一维成像分析;电子分析天平(精度0.000 1 g),测量不同时间间隔的样品质量;样品人工砂岩岩心为环氧树脂胶结石英砂,利用压机压制而成,尺寸均为1.5 cm×1.5 cm×5 cm,气测渗透率分别为4.5、10 D。
2.1.2 实验过程将气测渗透率分别为4.5、10 D的人工砂岩岩心(简称S1、S2)烘干、称重后,放于装有水的烧杯中,利用定水头装置保证吸水水位稳定,进行一维、三维不同边界条件的吸水实验,其中对一维垂向吸水实验的样品侧面用蜡进行密封处理,使得水分主要沿垂向运移,并将烧杯置于密封皿中;样品吸水不同时间间隔后取出,擦去表面水分,利用分析天平与MesoMR柜式核磁共振成像仪获取样品质量、T2谱与一维成像数据,直至样品吸水后质量不再变化,对测试结果进行整理、分析。
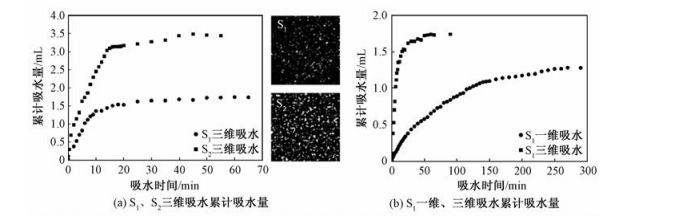
2.2 结果分析 2.2.1 砂岩毛细吸水性能分析研究砂岩的毛细吸水过程需对其吸水能力进行衡量与分析,本文利用核磁共振CPMG序列获取的衰减曲线首点信号量绘制累计吸水量曲线,分析不同渗透率、不同吸水条件对砂岩吸水量与吸水速率变化的影响。由图 2(a)可知,对于尺寸一致的人工砂岩样品,渗透率对其吸水能力影响显著。为更直观反映人工砂岩样品的孔隙结构,本文还利用CT技术对2个样品进行结构扫描,并对图片做二值化处理。结果显示,渗透率较高的样品吸水量更大、吸水速率更快,且渗透率与吸水量基本符合线性关系;而对于三维、一维两种吸水边界的实验,由图 2(b)可知,同一样品三维吸水过程由于与水分接触更充分,吸水速率远高于其一维吸水过程并较快达到稳定,且稳定后的累计吸水量也高于一维垂向吸水结果,吸水量较后者多30%左右。但仅根据吸水量变化难以分析水分的分布与运移状态,无法解释二者稳定吸水量的差异,这也是称重法的主要缺点,而核磁共振的谱分析与成像技术可获得更加全面的信息,后文将针对该问题进行深入分析。
|
Download:
|
| 图 2 S1、S2累计吸水量 Fig. 2 Cumulative water volumes of S1 and S2 by water absorption | |
此外,不同条件的吸水过程根据吸水速率变化皆可分为三部分:快速上升阶段、缓慢上升阶段以及相对稳定阶段。同时,将核磁共振数据与称重法数据相对比(如图 3所示),二者的含水量结果极为吻合。由此可知,核磁共振方法不仅在含水量的监测上具有较高的精度与可信度,而且可以监测水分运移过程,在岩石的吸水性能研究方面极具潜力。

|
Download:
|
| 图 3 核磁共振法与称重法结果对比 Fig. 3 Comparison of NMR with weighing method | |
通过CPMG序列反演得到不同孔隙中的水分分布信息是核磁共振方法相较称重法、电阻率成像法、计算机断层扫描法等方法研究毛细吸水问题的优势之一。对于砂岩吸水过程,核磁共振仪器可采集不同吸水时间后样品孔隙的水分分布信息,从而分析孔隙结构对该过程的影响与规律。如图 4(a)、4(b),反映人工砂岩样品S1、S2从开始三维吸水至稳定过程的孔隙水分变化情况。可见,人工砂岩的孔隙尺度分布较广,以大孔为主体,其吸水过程中各孔隙内的水分均匀增长,且较大孔隙内连通性较好,水分增长速度较快。通过谱分析也能明显观察到砂岩初始吸水速率快,之后逐步减缓的现象,而不同渗透率的样品在孔隙水分变化过程中存在共性。

|
Download:
|
| 图 4 S1、S2吸水横向弛豫谱 Fig. 4 Transverse relaxation T2 distributions of S1 and S2 by water absorption | |
此外,对S1样品进行不同吸水条件的水分分布比对,如图 4(c)可知,一维吸水条件的结果大体与三维吸水结果类似,水分在不同孔隙内均匀增加,且吸水速率随时间减缓。对比图 4(a)、图 4(c)可知,一维吸水相较三维吸水结果在较小的孔隙区域(横向弛豫时间10 ms附近)并未检测到水分信号,这有可能是人工砂岩岩心内部并未完全连通,使得一维吸水方式无法让水分迁移至部分孔隙中,因此一维吸水的累计含水量低于三维吸水的结果,具体可结合下文一维剖面成像结果进一步分析验证。
2.2.3 毛细吸水水分迁移规律通过成像原理直观观测砂岩吸水过程的水分分布与迁移过程,对于毛细吸水动力学特征与机理研究具有重要意义,核磁共振成像技术由于对水分独特的敏感性在相关领域研究具有广泛的适用性。此外,借助梯度场的一维剖面成像在测试精度方面又极具优势,故可提供砂岩毛细吸水过程的动态信息。
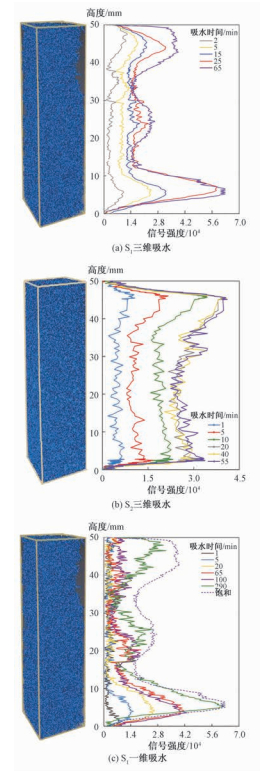
不同渗透率人工砂岩样品的不同位置水平截面含水量如图 5(a)、5(b)所示,对于三维吸水过程,水分由表面逐步向样品内部进入,且顶、底面由于直接接触水分,含水量增加略快于样品内部。本文还借助CT扫描数据,建立了三维孔隙结构。通过孔隙结构可以发现,S1样品的上部存在部分不连通孔隙,因此该段水平截面的含水量略低于其余位置,且与一维成像的水分分布数据对应较好。而S2样品整体连通性较好,水分迁移过程较为均匀,并最终均匀分布于整个样品之中。
|
Download:
|
| 图 5 S1、S2吸水核磁剖面成像结果 Fig. 5 NMR imaging results of S1 and S2 by water absorption | |
同时,本文也对S1样品的一维吸水水分迁移过程进行分析研究。该实验过程,样品底部与水分接触,随时间变化,毛细作用使得水分逐步由底部向顶部迁移,其一维剖面成像的水分迁移前缘逐步向上移动,最终达到稳定状态。图 5(c)中的虚线表示S1样品三维吸水稳定状态时的水分分布状态,可见二者整体趋势较为吻合,但在样品顶部由于孔隙连通性限制,一维吸水实验中水分并未能完全充满孔隙结构,使其水平截面的含水量略低。该结论也解释了上文部分孔隙区域中水分分布较少的现象。由此可见,孔隙结构与连通性对水分迁移途径与规律存在较大影响。
为深入研究水分迁移规律,本文还针对一维吸水过程进行定量化研究,将核磁共振方法结果与理论公式相结合,分析砂岩毛细吸水过程的动力学特征。目前,吸水率S(Sorptivity)被认为是最具代表性的毛细吸水特征评价指标[27],它反映不同介质在毛细力作用下吸收、运移水分的趋势与能力,可用于指示吸水速率[28]。该概念首先用于非饱和土壤带的水分运移研究,后逐步用于描述多孔介质的吸水过程。一维毛细吸水过程的吸水率[29]可通过以下公式求得:
| $ i\left( t \right) = k + S{t^{1/2}}, $ | (4) |
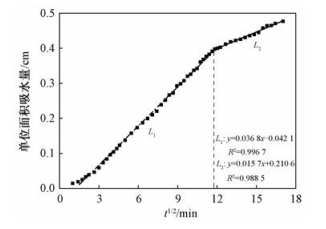
式中:i(t)为不同吸水时间单位横截面面积上的累计吸水量;k为一常数。该式反映一维吸水过程,其单位面积吸水量变化与t1/2成正比关系,则吸水率S可通过数据的线性拟合得到。人工砂岩样品S1的拟合结果如图 6所示,可见i-t1/2线性相关特征显著,然而在数据后段部分出现拐点,前后线性拟合斜率不同,即吸水过程中的吸水率发生变化。根据计算可得,前段吸水率约为0.036 8 cm/min1/2,后段吸水率约为0.015 7 cm/min1/2。
|
Download:
|
| 图 6 单位面积吸水量与t1/2关系图 Fig. 6 Cumulative water absorption vs. t1/2 | |
为了更好地解释该现象,我们将图 6与图 5(c)进行比对,发现图 6中拐点所处时间为水分迁移前缘到达顶端后,由此可推测,吸水率的变化与砂岩样品吸水条件变化有关。根据分析可知,在一维垂向吸水过程前段,水分迁移以毛细作用下的垂向上升为主,该过程中水分前缘逐步由底部向顶部迁移直至到达顶部,此阶段吸水率保持恒定。而此后,样品的吸水率减小,表现为图 6中L2段的斜率减小,可见存在某种作用影响水分的垂向迁移。对于本次实验而言,孔隙中水分丢失的途径仅有一种,即蒸发作用。人工砂岩S1进行一维垂向吸水时,一端持续吸水,而另一端当水分运移至顶端截面时受到蒸发影响,使得毛细作用下吸入的部分水分以蒸发的形式逃逸出样品系统,故表现为岩石吸水速率的减小[30-31]。因此,图中L1部分的线性拟合斜率更接近样品S1的真实吸水率,即为0.036 8 cm/min1/2。对图 6进一步分析可得,该实验条件下毛细吸水率大于蒸发率且最终二者达到平衡,故表现为水分迁移至样品顶端后,S1样品含水量仍增加并与t1/2呈线性关系。由此表明,蒸发效应对水分迁移条件的改变影响砂岩吸水过程。
通过一维剖面成像数据,本文对砂岩吸水过程进行更深入的研究与探讨,分析总结渗透率、吸水边界对水分迁移过程的影响,并定量化探讨吸水机理对吸水率的控制作用。
3 结论本文将核磁共振谱分析与一维成像技术相结合,对砂岩毛细吸水过程进行实验研究,并与称重法结果相对比,验证了核磁共振方法的精度与可信度。通过不同渗透率、吸水边界的核磁实验,可以归纳结论如下:
1) 利用核磁信号强度定量化表征累计吸水量、吸水速率随时间的变化,得到与常规认识一致的结论,三维吸水相较一维吸水条件吸水量更大,吸水速率更快,且砂岩的吸水过程大致可划分为快速上升阶段、缓慢上升阶段以及相对稳定阶段。同时,根据菲克定律计算得到一维垂向吸水条件下砂岩的吸水速率为0.036 8 cm/min1/2。
2) 通过核磁共振谱分析发现不同渗透率样品孔隙分布范围大致类似,结合成像技术与CT数据证明孔隙的连通性差异造成样品吸水量和吸水速率的不同,且砂岩吸水过程中不同尺寸孔隙内的水分均匀增加,其增加程度与速度受样品孔隙结构的影响。
3) 对于一维垂向吸水过程,其水分迁移机理的改变将导致吸水率的变化,水分运移至样品顶面后蒸发效应对于毛细吸水过程的影响不容忽视,蒸发强度的变化将直接影响岩石吸水特征。
综上所述,核磁共振技术作为一种直观、无损、快速、高精度的测试手段,对于孔隙介质水分迁移与水分分布相关问题的研究方面具有称重法、电阻率成像法、CT等方法不可比拟的优势。本文将核磁共振谱分析与成像技术相结合,分析不同岩性、孔隙度样品的吸水过程,并考虑蒸发效应的影响,有望进一步揭示孔隙介质中毛细吸水过程规律与特性。
| [1] | 李天斌, 陈子全, 陈国庆, 等. 不同含水率作用下砂岩的能量机制研究[J]. 岩土力学, 2015(s2):229–236. |
| [2] | Lockington D, Parlange J Y, Dux P. Sorptivity and the estimation of water penetration into unsaturated concrete[J]. Materials & Structures, 1999, 32(5):342–347. |
| [3] | Leventis A, Verganelakis D A, Halse M R, et al. Capillary imbibition and pore characterisation in cement pastes[J]. Transport in Porous Media, 2000, 39(2):143–157. DOI:10.1023/A:1006687114424 |
| [4] | Dehghanpour H, Lan Q, Saeed Y, et al. Spontaneous imbibition of brine and oil in gas shales:effect of water adsorption and resulting microfractures[J]. Energy & Fuels, 2013, 27(6):3039–3049. |
| [5] | Engelder T, Cathles L M, Bryndzia L T. The fate of residual treatment water in gas shale[J]. Journal of Unconventional Oil & Gas Resources, 2014, 7:33–48. |
| [6] | 蔡建超, 郁伯铭. 多孔介质自发渗吸研究进展[J]. 力学进展, 2012, 42(6):735–754. DOI:10.6052/1000-0992-11-096 |
| [7] | 黄蓓, 钱春香. 掺合料混凝土的毛细吸水现象[J]. 混凝土与水泥制品, 2008(4):14–16. |
| [8] | 李淑红, 王立成. 多孔建筑材料毛细吸水过程研究进展综述[J]. 水利与建筑工程学报, 2010, 8(6):16–20. |
| [9] | Washburn E W. The dynamics of capillary flow[J]. Physical Review, 1921, 17(3):273–283. DOI:10.1103/PhysRev.17.273 |
| [10] | Fries N, Dreyer M. An analytic solution of capillary rise restrained by gravity[J]. Journal of Colloid & Interface Science, 2008, 320(1):259–263. |
| [11] | Kim E, Whitesides G M. Imbibition and flow of wetting liquids in noncircular capillaries[J]. Journal of Physical Chemistry B, 1997, 101(6):855–863. DOI:10.1021/jp961594o |
| [12] | Cai J, Yu B, Zou M, et al. Fractal characterization of spontaneous co-current imbibition in porous media[J]. Energy & Fuels, 2010, 24(1):1860–1867. |
| [13] | 李科, 贾志刚, 余宏明, 等. 石膏质岩毛细吸水特性与孔隙特征研究[J]. 长江科学院院报, 2014, 31(9):79–83. |
| [14] | 任凯, 葛洪魁, 杨柳, 等. 页岩自吸实验及其在返排分析中的应用[J]. 科学技术与工程, 2015, 15(30):106–109. DOI:10.3969/j.issn.1671-1815.2015.30.019 |
| [15] | 贾志刚, 齐平, 李科, 等. 岩石毛细吸水试验新方法[J]. 长江科学院院报, 2015(5):95–99. |
| [16] | 查甫生, 刘松玉, 杜延军, 等. 基于电阻率法的膨胀土吸水膨胀过程中结构变化定量研究[J]. 岩土工程学报, 2008(12):1832–1839. DOI:10.3321/j.issn:1000-4548.2008.12.011 |
| [17] | Roels S, Carmeliet J. Analysis of moisture flow in porous materials using microfocus X-ray radiography[J]. International Journal of Heat & Mass Transfer, 2006, 49(s25/26):4762–4772. |
| [18] | Hanzic, Ilic R. Relationship between liquid and capillary in concrete[J]. Cement and Concrete Research, 2003, 33(9):1385–1388. DOI:10.1016/S0008-8846(03)00070-X |
| [19] | 蒙冕模, 葛洪魁, 纪文明, 等. 基于核磁共振技术研究页岩自发渗吸过程[J]. 特种油气藏, 2015(5):137–140. |
| [20] | Holmes W M, Packer K J. Investigation of two phase flow and phase trapping by secondary imbibition within Fontainebleau sandstone[J]. Magnetic Resonance Imaging, 2003, 21(s3/4):389–391. |
| [21] | 周莉, 何满潮, 李京阳, 等. 砂岩吸水特性试验[J]. 解放军理工大学学报(自然科学版), 2009, 10(6):580–585. |
| [22] | 司文朋, 魏建新, 狄帮让, 等. 人造砂岩制作方法及其声学性质研究[J]. 地球物理学进展, 2013, 28(4):2193–2198. DOI:10.6038/pg20130466 |
| [23] | Nestle N. NMR relaxometry study of cement hydration in the presence of different oxidic fine fraction materials[J]. Solid State Nuclear Magnetic Resonance, 2004, 25(1/3):80-83–84. |
| [24] | Tziotziou M, Karakosta E, Karatasios I, et al. Application of 1H NMR to hydration and porosity studies of lime-pozzolan mixtures[J]. Microporous & Mesoporous Materials, 2011, 139(1-3):16–24. |
| [25] | 俎栋林. 核磁共振成像学[M]. 北京: 高等教育出版社, 2004. |
| [26] | Jiang T, George Hirasaki A, Miller C, et al. Diluted bitumen water-in-oil emulsion stability and characterization by nuclear magnetic resonance (NMR) measurements†[J]. Energy & Fuels, 2007, 21(3):1325–1336. |
| [27] | Sabir B B, Wild S, O'Farrell M. A water sorptivity test for mortar and concrete[J]. Materials & Structures, 1998, 31(8):568–574. |
| [28] | Martys N S, Ferraris C F. Capillary transport in mortars and concrete[J]. Cement & Concrete Research, 1997, 27(5):747–760. |
| [29] | Wilson M A, Hoff W D, Hall C. Water movement in porous building materials-ⅩⅠ. Capillary absorption from a hemispherical cavity[J]. Building & Environment, 1994, 29(1):99–104. |
| [30] | Roels S. A comparison of different techniques to quantify moisture content profiles in porous building materials[J]. Journal of Thermal Envelope & Building Science, 2004, 27:261–276. |
| [31] | Lockington D A, Parlange J Y, Lenkopane M. Capillary absorption in porous sheets and surfaces subject to evaporation[J]. Transport in Porous Media, 2007, 68(1):29–36. DOI:10.1007/s11242-006-9056-5 |
 2017, Vol. 34
2017, Vol. 34 


