2. 中国科学院光电研究院, 北京 100094
2. Academy of Opto-Electronics, Chinese Academy of Sciences, Beijing 100094, China
基于衍射光学成像理论发展起来的现代衍射光学技术作为一项前沿学科在国内外得到快速发展[1-3]。在此基础上发展起来的叠层成像是一种无透镜的扫描相干衍射成像技术,于1969年由Hoppe和Strube提出并验证其有效性[4]。2004年Faulkner和Rodenburg[5]对Hoppe的叠层成像工作进行改进,提出基于相位恢复的叠层成像技术,该技术已经用于电子显微成像并获得目前该波段最好的分辨率与成像效果。2013年Shi等[6]将叠层成像用于光学图像加密中,实现叠层成像与信息安全的结合。2014年,Godden等[7]发明的三维叠层成像显微技术放宽了样品厚度的限制。目前叠层成像技术已在可见光域、X射线、电子显微镜等不同波段得到实验证实,相比于传统相位恢复算法,叠层衍射成像技术能够消除数值孔径对样品尺寸的限制,同时解决了正确解和复共轭之间的二义性问题,系统的复杂度显著降低[8]。近年,我们在叠层成像领域做了一些工作[9-12]。然而,在实际操作中,传统叠层成像技术照明光束的位置与理论位置间存在偏差,实验受随机噪声和系统噪声的干扰较大,这些都影响着图像的恢复质量。
目前,光学实验中常引入先验信息以提升成像质量。通常,在样品旁放置已知物体,并与样品共同记录,在迭代重建中将这些已知条件作为约束支撑,这些已知物体称为先验信息。在现阶段的研究中,常需借助其他光学器件建立先验信息和样品间的联系。如Alexander等[13]在物平面前放置相位物体以增加已知信息与待测样品的交叠面积,提升收敛速度和重建精度,有效地消除了“二义性”。此外,针对不同样品,先验信息的选取存在较多的限制条件。
考虑到上述情况,本文首次将先验信息引入叠层成像领域,提出一种基于已知振幅信息约束的叠层成像技术。本文通过计算机模拟实验和光学实验证实了该方法的有效性和通用性,同时针对系统的鲁棒性分析得到,该技术具有良好的抗噪能力、抗偏移能力和更快的收敛速度。该技术能够在保持叠层衍射成像技术的传统优势下,有效地解决上述先验信息的不足,实施过程简便,具有很好的通用性。
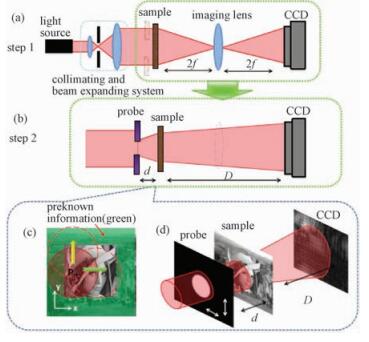
1 原理分析 1.1 已知先验信息的叠层成像技术的基本原理已知振幅型先验信息的叠层成像系统的原理如图 1所示。实验过程分为两步:利用成像透镜拍摄样品及其周围振幅图像,如图 1(a)所示;保证样品位置不变,撤下成像透镜放置孔径光阑。基于传统叠层衍射成像理论,以“过扫描”[14]的方式叠层扫描样品及其周围,经菲涅耳衍射最终记录各扫描位置对应衍射图样,如图 1(b)所示。所谓“过扫描”指衍射图样中应在保证交叠率和恢复效率的同时,尽量多地包含样品周围的已知信息。提取拍摄所得样品周围的已知信息,并将其作为重建基准,与衍射图样共同代入叠层迭代算法中,最终重建出待测样品的复振幅图像。由于迭代算法中包含准确的已知振幅信息,在重建恢复过程中,除层与层之间的交叠约束外,引入了样品周围的已知信息作为进一步的约束,有效地扩大已知条件,使重建结果更接近真实值。图 1(c)为已知先验信息的叠层扫描方式,其中样品周围绿色部分为先验信息,图 1(d)为叠层衍射成像的原理图。
|
Download:
|
| 图 1 已知先验信息的叠层成像技术的基本原理 Fig. 1 Principle of ptychographic imaging based on preknown information constraint | |
已知先验信息的叠层成像技术使用改进的ePIE算法[15],在ePIE的基础上增加对先验信息的读取-替换等步骤,利用已知图片的强度分布约束样品重建,提高成像质量。
本实验采用近场衍射,入射平面波通过扫描探针经过距离d的菲涅耳衍射照射在物面上,其中扫描探针的照明函数记为Pn(x, y),n=1, 2, …, m,物面的透过率函数为Oin(x, y),透过率函数由待测样品及其周围准确的先验信息构成。记录光强分布Iin代入算法中重建,光强分布由样品和已知信息的衍射斑构成。具体重建过程如下:
步骤1 由于第一次迭代时样品的透过率函数未知,因此透过率函数Oin(x, y)中样品部分为猜测值,其余部分为准确的振幅型先验信息,初始时i=1为迭代次数。
步骤2 探针Pn(x, y)透过物体后的出射场为
| $ {{\psi }_{\text{in}}}\left( \xi, \eta \right)={{P}_{n}}\left( x, y \right)\cdot {{O}_{\text{in}}}\left( x, y \right). $ | (1) |
步骤3 由菲涅耳变换得到出射场经过距离D传播到接收面时得到的振幅和相位
| $ \psi {{'}_{\text{in}}}\left( \xi, \eta \right)=\text{FrT}\left[{{\psi }_{\text{in}}}\left( \xi, \eta \right) \right], $ | (2) |
其中,将FrT定义为菲涅耳变换。
步骤4 应用已知的光强分布Iin对其振幅进行更新,得到新的强度分布为
| $ \psi {{'}_{\text{in}}}\left( \xi, \eta \right)={{I}_{\text{in}}}\cdot \left( \psi {{'}_{\text{in}}}\left( \xi, \eta \right)/|\psi {{'}_{\text{in}}}\left( \xi, \eta \right)| \right). $ | (3) |
步骤5 对更新后的光强分布进行逆菲涅耳变换,得到新的物面出射场
| $ {{\psi }_{\text{new}}}\left( \xi, \eta \right)=\text{Fr}{{\text{T}}^{-1}}\left[\psi {{'}_{\text{in}}}\left( \xi, \eta \right) \right], $ | (4) |
其中,将FrT-1定义为逆菲涅耳变换。
步骤6 令Δψ(ξ, η)=ψnew(ξ, η)-ψin(ξ, η),更新样品的物函数和探针
| $ {{O}_{\text{in}}}\left( x, y \right)=U\left[{{O}_{\text{in}}}\left( x, y \right), {{P}_{n}}\left( x, y \right), \Delta \psi \left( \xi, \eta \right) \right], $ | (5) |
| $ {{P}_{n}}\left( x, y \right)=U\left[{{P}_{n}}\left( x, y \right), {{O}_{\text{in}}}\left( x, y \right), \Delta \psi \left( \xi, \eta \right) \right], $ | (6) |
其中U为更新系数:
| $ U\left[f, g, \Delta \psi \right]=f+\alpha \frac{{{g}^{*}}}{|g|_{\max }^{2}}\Delta \psi, $ |
其中,α为反馈函数,以下模拟实验中取1。
步骤7 提取更新后物函数中样品部分,替换初始物函数中样品,作为新的物函数Oin(x, y),Oin(x, y)由重建后样品复振幅图像及其周围准确的先验信息构成。移动至下一照明探针Pn(x, y) (n=n+1),重复步骤2到步骤6遍历所有照明位置。
步骤8 当计算完所有探针,视为完成一轮迭代。当迭代阈值达到要求值时,完成迭代,得到最终的重建物函数。
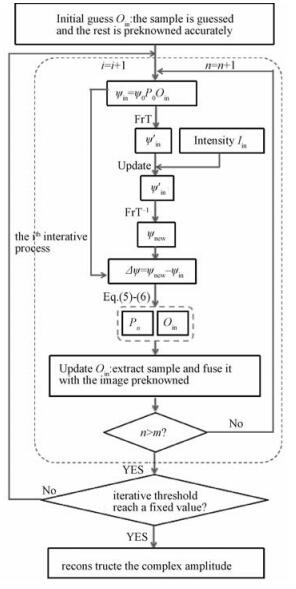
以上算法可用如图 2所示流程图表示。
|
Download:
|
| 图 2 已知先验信息的叠层成像算法流程图 Fig. 2 Flow chart of ptychographic imaging algorithm based on preknown information constraint | |
模拟实验中分别采用“lena”和“baboon”作为待测样品的振幅和相位,如图 3(a)和图 3(b)所示。采用“flat”作为已知信息(图 3(c))。利用待测样品替换图 3(c)中黑色部分,表示在样品周围引入先验图像(图 3(d))。有效采样点为256×256,照射光束为632.8 nm,共扫描4×4个孔径位置(图 3(e))。

|
Download:
|
| 图 3 初始模拟数据 Fig. 3 Initial simulation data | |
值得注意的是,本法在叠层衍射成像中有较强的适用性,对于其他拓展型算法,仍可将样品周围振幅分布视为先验信息,通过已知条件进行约束提升恢复效果。限于篇幅,本文仅以比较传统叠层成像方法为例进行一般性说明,对其他拓展算法不再详述。
分别迭代50次观察重建结果,为了能够微观地分析复原效果和收敛速度,引入复原结果与原样品的相关系数Co及均方差MSE。振幅和相位结果及曲线图如图 4所示。可以发现,已知先验信息的叠层成像技术的复原效果明显好于传统叠层成像技术,特别在相位恢复上提升效果显著,且收敛速度明显提高。而由于传统叠层成像方法已经能够很好地恢复出样品的振幅信息,所以直观上两种方法复原结果对比不明显。但本文技术相比传统技术收敛速度增加近一倍;对比图 4(e)和图 4(f),利用传统叠层成像技术重建相位时部分信息出现反转现象,而通过本文方法很好地修复了这一问题,相位复原结果更加清晰完整。

|
Download:
|
| 图 4 利用两种算法重建结果对比 Fig. 4 Comparison of the reconstruction results between the two ptychographic methods | |
上述结果中基于先验信息的叠层成像技术在振幅和相位的重建结果及收敛速度上均有明显提高,由于篇幅有限,以下讨论中仅以相位重建为例,对抗噪声和抗孔径偏移能力进行分析。
2.2 噪声对两种成像技术的影响已知先验信息的叠层成像方法相比于传统方法具有更强的抗噪声能力。通过分析实际情况和上述模拟实验条件,我们在每幅衍射图中引入50%的随机噪声,以此比较两种叠层衍射成像方法重建得到的复原结果。图 5是相位部分迭代50次的重建结果及其相关系数Co和均方差MSE。

|
Download:
|
| 图 5 50%噪声迭代50次时重建结果及曲线图 Fig. 5 Reconstructions and their graphs after 50 iterations with 50% random noise | |
可以看到,引入50%的随机噪声后,在相位相关系数曲线中,传统叠层成像技术的Co稳定值约为0.68,而本文技术的Co稳定值可达到0.91,且收敛速度为传统方法的3倍。在均方差曲线中,本文技术的优越性也能很好地体现。综上所述,已知先验信息的成像方法受噪声干扰较小,相位信息恢复更全面,具有更好的收敛性。
2.3 孔径偏移对两种成像技术的影响由于目前光学设备的精度有限,不可避免地存在孔径的偏移误差,从而影响实验结果。已知先验信息的叠层成像技术相比于传统技术具有更好的抗孔径偏移能力。模拟实验中,我们对P1、P4和P15等3个扫描孔径的位置添加平移误差,模拟迭代50次时两种方法重建得到的复原结果及其相关系数Co和均方差MSE,如图 6所示。

|
Download:
|
| 图 6 个孔径位置偏移下迭代50次的重建结果及曲线图 Fig. 6 Reconstructions and their graphs after 50 iterations using three probes in wrong positions | |
面对相同偏移误差,利用本文方法进行恢复,相位重建效果更加清晰完整。由图 6(c)~6(d)可知,当存在孔径偏移时,相同迭代次数下,利用已知先验信息的叠层成像方法重建得到的相位Co值更大,MSE值更小,收敛速度更快,由此证实了在已知先验信息的条件下,叠层成像技术具有更好的抗孔径偏移能力。
3 光学实验分析 3.1 实验装置我们搭建了一个光学叠层衍射成像系统进一步分析本文所提方法的有效性。实验装置如图 7所示,光源为波长为632.8 nm的氦氖激光器,通过扩束准直系统获得入射平面波。首先放置成像透镜,并在其后接收样品及其周围图像的等大倒像。实验中将激光通过成像透镜照射得到样品周围的已知信息作为先验约束条件。然后保证待测样品位置不变,撤下成像透镜,放置探针并进行移动,对样品的不同部分“过扫描”进行衍射成像。

|
Download:
|
| 图 7 已知先验信息的叠层成像实验装置图 Fig. 7 Optical setup of ptychography based on preknown information constraint | |
模拟实验中,待测样品四周为“flat”图片,即准确的振幅信息。与模拟实验不同的是,实验中利用相干光作为光源,存在相干噪声和散斑噪声,所以采集得到的先验信息并不完全准确。通过光学实验的叠层重建结果可以看出,采用相干光照明能够很好地完成样品复振幅的恢复,且在相同的实验环境下,恢复效果相比于传统叠层技术有较大提升,因此可以推知当采用非相干光照明获得更精确的先验信息时,叠层重建结果将更加清晰准确。本实验利用相干光做点光源,既能够保证叠层成像技术的重建质量,又无需在实验过程中更换光源,减少操作和实验成本,因此在实际应用中具有一定价值。
实验中接收衍射图样所使用的CCD为Coolsnap EZ型,单像素尺寸为6.45 μm,CCD窗口大小为1 392×1 040像素。本实验中的样品分别为分辨率板(美军标MIL-S-150A)和植物茎横切组织。
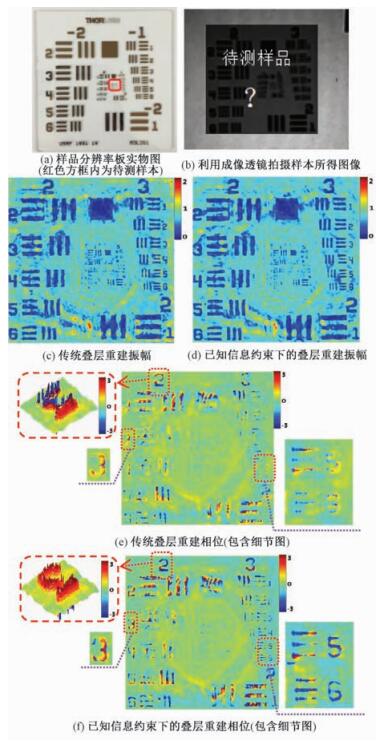
3.2 重建结果及分析 3.2.1 分辨率板复原效果及分析首先采用分辨率板作为实验样品。实验中,探针移动3×3个位置,每次移动1 mm,探针直径为5.50 mm。探针与待测样品间距离d为33.80 mm,样品与CCD间距离D为84.92 mm。图 8(a)为数码相机拍摄所得分辨率板实物图,选取其中最小图块为待测样品并用红框标出。8(b)为经凸透镜成像并用CCD接收获得的样品及其周围图像的振幅信息,实验中将激光通过样品周围透明玻璃片照在CCD上,采集得到图像作为已知约束条件。图 8(c)~8(f)为采用两种算法恢复结果,迭代次数均为20次。
|
Download:
|
| 图 8 待测样品及两种叠层成像重建结果 Fig. 8 Sample and the reconstruction results using traditional ptychography and ptychography based on pre-known constraint | |
对比图 8(c)、8(d)看出,基于已知先验信息的叠层成像方法重建出的振幅图像质量与传统叠层成像方法比较接近,但对比度要略好于传统叠层成像技术;对比图 8(e)、8(f),传统叠层方法的重建图像十分模糊,数字几乎不可见,而利用本文方法重建出的相位图像线条清晰,色彩对比度更高,由此表明相位分辨率更高,恢复质量更好。将相位图像中圈出部分放大观察,待测样品的细节相比传统叠层成像更加完整。同时取样品部分三维图,可以直观地看出,本文方法成像效果更好,相位信息连续性增强,更接近真实情况。由此可见,在相同的实验环境下,采用本文方法重建所得复振幅信息相比于传统方法有一定提升,且无需增加实验成本,因此具有实际意义。
3.2.2 植物茎横切组织复原效果及分析由于分辨率板属于纯振幅样品,复原的相位信息不能完全反映叠层衍射成像技术的水平,下面采用植物茎横切组织样品,以便能够在振幅和相位上完全反映叠层衍射成像的复原效果。实验中探针移动3×3个位置,每次移动1 mm,探针直径为5.95 mm。探针与待测样品间距离d为28.84 mm,样品与CCD间距离D为91.96 mm。图 9(a)为利用成像透镜成像,在接收器上显示的样品及其周围所成图像,实验中仍以光通过样品周围透明玻璃片照在CCD上所采集的图像作为已知约束条件。图 9(b)~9(e)为对两种算法均迭代20次后的恢复结果。

|
Download:
|
| 图 9 待测样品及两种叠层成像重建结果 Fig. 9 Sample and the reconstruction results using traditional ptychography and ptychography based on preknown constraint | |
观察成像透镜拍摄得到的样品图和基于叠层衍射成像重建得到的复振幅图像可知,重建样品轮廓鲜明,在细节上信息更加丰富。对比图 9(b)~9(c),采用本文方法恢复得到的振幅图像效果有一定提升,结合图中圈出部分的放大图可以看出,在已知信息的约束下,植物组织细胞的脉络线条分明,能够更好地反映样品内部的实际结构;对比图 9(d)、9(e),相位重建信息色彩丰富,辨识度提高。为了能够直观的观察样品的空间结构,分别重建出样品振幅和相位的三维分布图,进一步验证了利用已知信息能够在振幅和相位上显著加强重建结果的连续性,使样品更接近真实情况。综合分辨率板实验中的重建结果,可以证明本文技术具有良好的通用性和实用性。
4 总结本文利用模拟实验和光学实验分别验证了基于已知振幅信息约束的叠层衍射成像技术在样品重建上的效果,并通过相关系数Co和协方差MSE曲线进行定量分析,加强所提出理论的可靠性。实验结果证明:在相同实验环境下,基于振幅型先验信息的叠层衍射成像技术相比于传统叠层成像技术能够有效地提高样品的恢复质量和收敛速度,相位重建效果尤其显著,此外该技术具有更强的抗噪声和抗孔径偏移能力。模拟实验和光路实验在误差允许范围内很好地吻合,证明了实验成像装置的可靠性。同时在光学实验中对多个样品进行探究,验证了本方法具有广泛的通用性。本方法成像过程简便,实际操作中,无需提高实验成本,具有较强的实用性,在叠层成像领域具有比较重要的参考价值。
| [1] | Miao J, Charalambous P, Kirz J, et al. Extending the methodology of X-ray crystallography to allow imaging of micrometre-sized non-crystalline specimens[J]. Nature, 1999, 400(6742):342–344. DOI:10.1038/22498 |
| [2] | Thibault P, Dierolf M, Bunk O, et al. Probe retrieval in ptychographic coherent diffractive imaging[J]. Ultramicroscopy, 2009, 109(4):338–343. DOI:10.1016/j.ultramic.2008.12.011 |
| [3] | Rodenburg J M. Ptychography and related diffractive imaging methods[J]. Physics, 2008, 150:87–184. |
| [4] | Hoppe W, Strube G. Diffraction in inhomogeneous primary wave fıelds. 2. Optical experiments for phase determination of lattice interferences[J]. Acta Crystallogr A, 1969, 25:502–507. DOI:10.1107/S0567739469001057 |
| [5] | Faulkner H M L, Rodenburg J M. A phase retrieval algorithm for shifting illumination[J]. Applied Physics Letters, 2004, 85(20):4795–4797. DOI:10.1063/1.1823034 |
| [6] | Shi Y S, Li T, Wang Y L, et al. Optical image encryption via ptychography[J]. Optics Letters, 2013, 38(9):1425–1427. DOI:10.1364/OL.38.001425 |
| [7] | Godden T M, Suman R, Humphry M J, et al. Ptychographic microscope for three-dimensional imaging[J]. Optics Express, 2014, 22(10):12513. DOI:10.1364/OE.22.012513 |
| [8] | 王治昊, 李拓, 王雅丽, 等. 基于旋转相位编码与照明光束匹配的叠层衍射成像算法研究[J]. 物理学报, 2014, 63(16):191–197. |
| [9] | 王雅丽, 史祎诗, 李拓, 等. 可见光域叠层成像中照明光束的关键参量研究[J]. 物理学报, 2013, 62(6):201–210. |
| [10] | Li T, Shi Y S. Security risk of diffractive-imaging-based optical cryptosystem[J]. Opt Express, 2015, 23(16):21384–21391. DOI:10.1364/OE.23.021384 |
| [11] | Li T, Shi Y S. Attack on optical double random phase encryption based on the principle of ptychographical imaging[J]. Chinese Physics Letters, 2016, 33(1):63–66. |
| [12] | 刘祥磊, 潘泽, 王雅丽, 等. 基于叠层衍射的数字水印算法研究[J]. 物理学报, 2015, 64(23):85–94. |
| [13] | Alexander J, Walter H, Stefan B, et al. Quantitative single-shot imaging of complex objects using phase retrieval with a designed periphery[J]. Optics Express, 2012, 20(5):5470–5480. DOI:10.1364/OE.20.005470 |
| [14] | 周光照, 佟亚军, 陈灿, 等. 相干X射线衍射成像的数字模拟研究[J]. 物理学报, 2011, 60(2):772–778. |
| [15] | Maiden A M, Rodenburg J M. An improved ptychographical phase retrieval algorithm for diffractive imaging[J]. Ultramicroscopy, 2009, 109(10):1256–1262. DOI:10.1016/j.ultramic.2009.05.012 |
 2017, Vol. 34
2017, Vol. 34 


