2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
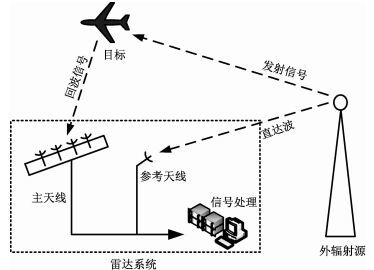
外辐射源雷达具有在静默状态下实现目标探测的特点,近年来已成为研究热点[1-2]。基于全向外辐射源的雷达系统主要由主天线、参考天线、回波通道和参考通道接收机、信号处理器等组成,如图 1所示。回波通道接收从目标散射回来的目标回波信号,参考通道接收外辐射源的直达波参考信号。回波通道进行直达波对消处理后,将回波信号与参考信号经匹配滤波和相干积累处理后获得目标的距离-多普勒谱,从而进行目标的检测及定位。
|
Download:
|
|
图 1 外辐射源单源单站雷达系统结构示意图 Fig. 1 Geometry of passive radar system of SISO |
|
除单源单站工作方式外,外辐射源雷达也可工作在单源多站、多源单站、多源多站方式下。
广播和电视信号是一类重要的全向外辐射源,具有带宽大、发射功率稳定、低空覆盖区域广等优点,可用来形成空中目标雷达探测系统[3]。FM广播信号具有较大的发射功率,适合用于外辐射源雷达远距探测,但较低的信号频率和较小的带宽使雷达的距离和角度分辨率受限。DVB-T数字电视信号具有较高的发射功率,其信号频率较高、带宽较大,有助于外辐射雷达实现远距离高分辨率探测。
基于数字电视信号的相关参数,本文主要分析全向外辐射源雷达的空中目标探测性能。
1 主要问题及系统体制损失 1.1 参考信号获取问题与传统雷达不同,外辐射源雷达存在参考信号获取问题。参考信号在外辐射源雷达中主要有两个作用,一是用来对消回波通道中的直达波及多径杂波;二是用来重构发射信号对目标回波进行时延和多普勒频移两维匹配滤波,以实现目标检测和参数估计。
参考信号获取主要有两种途径:第一种是根据外辐射源的位置信息,设置方向性强的参考天线接收外辐射源的直达波信号;第二种是根据广播电视信号的波形特征直接对参考信号进行重构,例如恒模算法[4]、基于编解码的重构算法[5-6]等。目前技术水平下,接收站参考信号的获取主要通过独立设置的定向参考天线接收直达波信号实现,对固定接收站,有条件时可考虑在收发站间铺设光缆,传输发射信号,形成失真较小的参考信号。
无论采用哪种途径获取参考信号,由于电磁波在空间传播过程中路径与回波通道存在差异,参考信号与目标回波信号都存在去相关问题,并会在匹配滤波环节产生去相关失配损失,对此在实际系统设计中应予以考虑。
使用参考天线获取直达波,假定外辐射源发射天线高度100 m,接收站参考天线高度9 m,对应的通视距离约50 km。当收发站间距50 km时,由于地球曲率影响,参考天线收到直达波困难;当收发站间距40 km时,由于地形和地物遮挡的影响,参考天线中多径直达波功率和直达波功率有可能达到相当的水平,由此会和目标回波信号产生2~3 dB的去相关损失。多径直达波主要来自于近距离地物,接收站周围地形越开阔、直达波方向地物越少,参考天线的高度越高,波束越窄,副瓣越低,多径直达波影响越小。
参考信号中多径直达波的存在,不仅会产生去相关失配损失,而且会降低直达波的时域对消效果,产生虚假目标并增加虚警概率,因此必须对其进行提纯处理。数字电视信号的带宽较宽,距离分辨率较高,当直达波分量较弱,基于主成分分析的提纯方法[7]效果有限时,可开展基于高距离分辨率特征的直达波提纯研究工作。
1.2 直达波抑制问题外辐射源雷达的直达波抑制问题类似传统连续波雷达的收发隔离问题,由于其直接影响雷达的探测灵敏度和作用距离,是外辐射源雷达要解决的核心问题,在系统设计中要有充分考虑,目前分空域抑制和时域抑制两个环节。
1) 空域抑制
直达波空域抑制的主要方法是主天线采用低副瓣天线或在主天线产生方向图凹口对准外辐射源,减少直达波进入接收机的功率,并使用大动态范围接收机和多位数AD。空域干扰抑制对副瓣干扰具有较好的抑制效果,但对于主瓣内的多径干扰无抑制能力。
假定通过相干积累预期实现的信噪比改善因子为60 dB (如脉冲压缩时宽带宽积为30 dB,慢时间域1 000个脉冲相干积累增益为30 dB),基于16位AD的仿真分析表明[8]:当输入信噪比为-40 dB,输入杂噪比为0~60 dB,为保证小信号无损失采样和大信号不出现多普勒频谱杂散,接收机噪声电平应淹没AD8位,由此确定接收机增益和动态范围,此时输入杂噪比为60 dB的信号已使16位AD接近饱和,显然为保证小信号探测能力提高接收机噪声电平,会使16位AD的动态范围有较大缩小。
将直达波看做杂波,上述分析表明空域抑制应保证直达波信号功率不大于接收机灵敏度60 dB。当进入接收机的直达波信号功率较大时,为避免AD饱和可降低接收机增益,但由此会产生目标检测损失,这实际上明确了空域直达波抑制的要求。
主天线收到的直达波功率与收发站间距和主天线的副瓣电平相关,主天线收到的直达波信号功率计算公式如下
| ${P_{\rm{d}}} = \frac{{{P_{\rm{t}}}{G_{\rm{t}}}{G_{{\rm{er}}}}{\lambda ^2}}}{{{{\left( {4{\rm{\pi }}} \right)}^2}{D^2}}},$ | (1) |
其中:辐射源的平均发射功率为Pt;发射天线增益为Gt;主天线在辐射源方向的接收增益为Ger;信号波长为λ;辐射源到接收站距离为D。
外辐射源系统参数如表 1所示。当收发站间20 km,主天线对直达波接收增益Ger=5 dB时,主天线收到的直达波产生的杂噪比已接近60 dB;当收发站间距40 km,主天线对直达波接收增益Ger=-10 dB时,主天线收到的直达波产生的杂噪比接近40 dB。在实际系统中,由于要兼顾参考信号接收,收发站间距不能太大,要实现主天线对直达波接收增益达到-10 dB并非易事,由于在此波段天线副瓣不可能很低,只能通过在辐射源方向使天线副瓣区自适应形成凹口[9],或者机械移动主天线使方向图凹口对准外辐射源。小尺寸宽波束天线一般具有较低的副瓣,且容易采用机械方式使方向图凹口对准外辐射源。
|
|
表 1 单源单站系统参数 Table 1 Related parameters of single illuminator and single observer system |
2) 时域抑制
目前直达波的时域抑制方法主要为自适应杂波对消方法[9-10]。文献[11]分析直达波时域抑制方法的性能,其性能主要由参考信号和主天线收到的直达波信号的相关系数决定,并将其转化为参考通道和接收通道的一致性问题。结合直达波抑制算法,在目前技术水平下直达波时域对消增益可达到35 dB。假定空域抑制使直达波杂噪比在40 dB水平,时域对消后剩余5 dB的杂噪比仍会对目标的探测性能产生影响。
由于广播电视信号是一类随机信号,其模糊函数为图钉型,距离-多普勒平面副瓣较高,其直达波抑制的杂波剩余会提高距离-多普勒平面的检测基底,并直接影响目标探测性能,故其测试是一项重要的工作内容。考虑到近距离静止杂波空间分布的影响,应在距离-多普勒平面分远近距和高低多普勒频率区间测试,其比对值应为仅有接收机噪声条件下的距离-多普勒平面基底。
要特别注意的是,目前基于LMS算法实施杂波对消处理后,杂波残余功率最多会被降低到噪声功率水平[11]。杂波残余会使检测基底升高,即使参考信号中没有噪声,杂波对消环节也会带来3 dB的检测损失。当参考信号存在噪声或多径直达波时,杂波残余会增大到参考通道噪声加多径直达波水平并由此产生更大的检测损失。
1.3 数字电视信号特有问题1) 信号频率高和带宽大
外辐射源雷达系统辐射源与接收站分置的观测结构,对于运动目标在原理上就容易产生多普勒散焦。数字电视信号频率较高,对具有横向速度的运动目标更容易产生多普勒散焦,从而降低探测性能。与此同时,由于其带宽较大,等效的距离分辨率比较高,约8 MHz的信号带宽对应的距离分辨率约为20 m,当目标径向运动速度较高为300 m/s,信号积累时间为1 s时,存在15个距离单元跨越问题。由此产生的距离徙动会造成较大的探测性能损失。
目前,距离徙动可采用keystone变换实施校正[12],以减少探测损失。外辐射源雷达天线波束通常不扫描,对远距离目标信号可采用长时间相干积累,对近距离目标信号可采用短时间相干积累,并自动实现一定的灵敏度时间控制(STC)功能。由于运动目标的多普勒散焦程度与距离成反比,对远近距离目标采用不同信号积累时间并形成不同的数据率,不仅是一个合理的选择,显然也有利于缓解目标多普勒散焦问题。
当信号频率500 MHz,目标横向运动速度300 m/s,距离50 km,信号积累时间1 s,多普勒散焦可达6 Hz,远大于多普勒频率分辨率1 Hz,会产生较大的信噪比损失。把信号积累时间调整为0.3 s,由于2 Hz的多普勒散焦值小于3 Hz的多普勒频率分辨率,可避免多普勒散焦带来的探测损失。
当目标径向运动速度300 m/s时,其对应的多普勒中心频率可达到1 kHz,这意味着系统的等效重复频率至少要达到2 kHz,由此限制了系统的不模糊测距离范围仅为75 km。为了综合解决不模糊测距/测速以及距离徙动/多普勒散焦问题,可考虑将约8 MHz带宽的电视信号进行频率分割,形成等效载频为4 MHz的长波长信号,再使用双频共轭处理去除多普勒模糊完成低信噪比高速运动目标探测和参数估计[13]。
2) 多站单频网
数字电视信号目前采用多站组网结构在降低发射功率的同时提高覆盖范围,客观上形成了分布式的外辐射源,而且单频网已成为主要的发展方向。为了保证地面用户的使用,其信号在高度方向的覆盖范围有限,这在原理上限制了基于单接收站的外辐射源雷达系统的探测距离,因此研究基于组网方式的多源多站(包括单源三站)雷达系统具有重要的意义。
不同于简单的单频网,数字电视单频网是指网中若干发射点同时在同一频带发射相同信号,依托先进的调制解调技术可防止同频带发射站间互扰,实现对一定服务区域的可靠覆盖。由于可得到各个发射站调制解调的先验信息,在原理上可考虑通过信号处理的方法实现多源同频信号的分选。文献[14]介绍压缩感知(CS)理论在外辐射源雷达中的应用情况,其核心思想为在信号的匹配滤波环节上通过使用CS方法抑制随机信号副瓣的干扰,提高空间分辨率和目标定位精度。将CS方法引入数字电视单频网外辐射源雷达系统,有可能同时提高直达波抑制能力,相关研究工作值得深入开展。
以上论述数字电视信号外辐射源雷达的特有问题,由此可能产生的系统性能损失在实际应用中应予以重视。
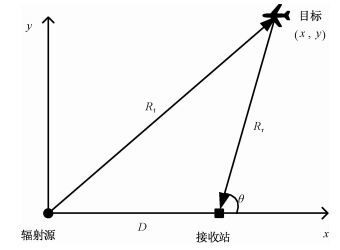
2 单源单站系统性能分析 2.1 单源单站系统参数单源单站系统通常采用测量目标双基距离和方位角实现对目标的定位[15],辐射源与接收站的系统布局如图 2所示。图中Rt为辐射源到目标距离,Rr为接收站到目标距离,D为辐射源到接收站基线长度,θ为目标相对接收站的方位角。
|
Download:
|
|
图 2 单源单站系统布局 Fig. 2 Layout of passive radar system of SISO |
|
单站考虑使用4组阵列天线,每组在方位向覆盖90°即可实现全向覆盖。每组天线由俯仰4×方位6阵元组成,俯仰上每4个阵元采用功率合成后,俯仰向覆盖范围约为26°(3 dB波束宽度)/36°(6 dB波束宽度),在方位向形成6个通道,通过DBF形成5个方位波束,每个方位波束覆盖约17°(3d B波束宽度),方位向覆盖范围约85°[16-17]。系统的总波束数为4×5,对应的信号处理通道数为20。系统参数如表 1所示。
这里检测信噪比选取为16 dB,对应起伏目标的发现概率约为0.8,虚警约为10-5[18];系统损耗选取为13 dB,包括射频系统损失1 dB,波束形状损失1 dB,CFAR损失2 dB,信号处理失配损失5 dB (包括AD、目标距离徙动、多普勒散焦、滤波器带宽失配等),参考信号与回波信号去相关损失1 dB (相关系数0.8),直达波对消使检测基底抬高损失3 dB,后两项损失为外辐射源雷达体制带来的。显然上述参数的设置较为理想,实际的系统损耗可能会更大。
2.2 单源单站探测能力根据信号从辐射源到接收机传播中的功率变化情况,由雷达方程[18]可推导出
| ${R_{\rm{r}}}{R_{\rm{t}}} = \sqrt {\frac{{{P_{\rm{t}}}{G_{\rm{t}}}{G_{\rm{r}}}\sigma {\lambda ^2}}}{{{{\left( {4{\rm{\pi }}} \right)}^3}k{T_0}(1/{T_n}){\rm{ }}F{L_n}{{\left( {SNR} \right)}_{{\rm{omin}}}}}}} ,$ | (2) |
其中:Pt为辐射源发射功率;Gt为发射天线增益;Gr为接收天线增益;σ为目标RCS;λ为信号波长;Rt为目标到辐射源距离;Rr为目标到接收天线的最远接收距离;(SNR)omin为接收机最小输出信噪比;k为波尔兹曼常数;T0为接收机噪声温度;F为接收机噪声系数;Tn为接收机信号积累时间;Ln为系统损耗。
根据图 2及式(2) 可得到雷达在水平面各个方向上的最大接收距离表达式
| ${R_{{\rm{rmax}}}} = \sqrt {\frac{{{P_{\rm{t}}}{G_{\rm{t}}}{G_{\rm{r}}}\sigma {\lambda ^2}}}{{{{\left( {4{\rm{\pi }}} \right)}^3}k{T_0}(1/{T_n}){\rm{ }}F{L_n}{{\left( {SNR} \right)}_{{\rm{omin}}}}}} + \frac{{{D^2}}}{4} + \frac{D}{2}} ,$ | (3) |
| ${R_{{\rm{rmin}}}} = \sqrt {\frac{{{P_{\rm{t}}}{G_{\rm{t}}}{G_{\rm{r}}}\sigma {\lambda ^2}}}{{{{\left( {4{\rm{\pi }}} \right)}^3}k{T_0}(1/{T_n}){\rm{ }}F{L_n}{{\left( {SNR} \right)}_{{\rm{omin}}}}}} + \frac{{{D^2}}}{4} - \frac{D}{2}} .$ | (4) |
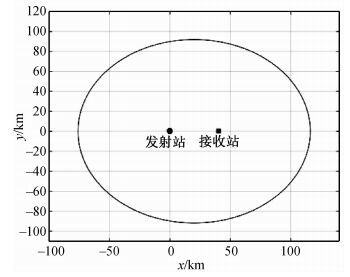
在表 1参数下,Rrmax=116 km,Rrmin=76 km,单站覆盖范围约为28 953 km2,如图 3所示。
|
Download:
|
|
图 3 单源单站系统平面布局及覆盖范围 Fig. 3 Layout and coverage area of passive radar system of SISO |
|
单源单站系统通常利用目标的双基距离和方位角实现对目标的定位,一般不测量目标高度。其双基距离测量精度主要由信号带宽、GPS时统精度、辐射源和接收站的定位精度。对基于数字电视信号的雷达系统而言,其双基测量精度已可以优于100 m;其方位角测量精度通常在天线方位波束宽度的1/10左右。假定天线的方位波束宽度为10°,其方位角测量精度约1°。测角方法主要由比幅测角与和差测角两种。要提高方位角的测量精度,需要增大天线尺寸。
在图 2所示的单源单站系统布局中,设接收站接收到辐射源的直达波与经目标反射的回波之间的时间延迟为Δt,目标的双基距离为R。
根据三角函数关系有
| $R_{\rm{t}}^2 = R_{\rm{r}}^2 + {D^2} + 2{R_{\rm{r}}}D\cos \theta .$ | (5) |
目标的双基距离是目标到辐射源距离与目标到接收站距离之和,即
| $R = {R_{\rm{t}}} + {R_{\rm{r}}} = c\Delta t - D.$ | (6) |
根据式(5) 和式(6) 可推出目标到接收站距离的表达式
| ${R_{\rm{r}}} = \frac{{{R^2} - {D^2}}}{{2\left( {R + D\cos \theta } \right)}}.$ | (7) |
由此再结合图 2所示的单源单站系统布局,可得到目标位置x、y关于双基距离和方位角的表达式,
| $\left\{ \begin{array}{l} x = D + {R_{\rm{r}}}\cos \theta ,\\ y = {R_{\rm{r}}}\sin \theta . \end{array} \right.$ | (8) |
进而根据全微分方程可求得目标的位置精度,
| $\left\{ \begin{array}{l} {\rm{d}}x = \left| {\cos \theta } \right|{\rm{d}}{R_r} + \left| {{R_{\rm{r}}}\sin \theta } \right|{\rm{d}}\theta ,\\ {\rm{d}}y = \left| {\sin \theta } \right|{\rm{d}}{R_r} + \left| {{R_{\rm{r}}}\cos \theta } \right|{\rm{d}}\theta . \end{array} \right.$ | (9) |
表 2给出不同参数下的目标位置测量精度仿真结果。
|
|
表 2 单源单站目标位置测量精度仿真结果 Table 2 Measurement accuracy simulation results of target location in SISO |
从表 2的仿真结果可以看出,在单源单站条件下,基于双基距离和方位角可对目标在x、y方向上实现定位,其位置测量精度与目标距离有关,距离越远,定位精度越低。在双基距离测量精度100 m、方位角测量精度1°的条件下,在双基距离200 km处定位精度约为1.7 km。单源单站对目标的定位精度主要受限于测角精度。
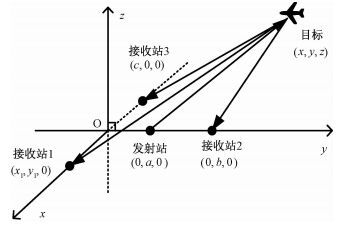
3 单源三站系统性能分析 3.1 单源三站系统参数下面以1个辐射源、3个接收站为例分析单源多站情况。3个接收站以辐射源为中心成“Y”型布局,如图 4所示。图中定义x,y,z为目标在该坐标系中的直角坐标。为发射站到接收站基线长度。为满足“Y”型布局要求,设置辐射源、接收站位置关系如图中所示,辐射源与接收站2位于y轴上,接收站1和接收站3位于x轴上。这里a=0.5D,b=1.5D,c=-0.866D,x1=0.866D,y1=0。
|
Download:
|
|
图 4 单源三站(SITO)系统布局 Fig. 4 Layout of passive radar system of SITO |
|
这里3个接收站使用的接收天线总阵元数为96个,与单源单站工作方式下一致。每个接收站阵元数为32个,考虑使用4组阵列天线,每组在方位向覆盖90°以实现全向覆盖,如图 5所示。接收站每组天线由俯仰4×方位2阵元组成,采用功率合成后形成1个通道,方位向覆盖约60°(3 dB波束宽度)/85°(6 dB波束宽度),俯仰上覆盖范围约为26°(3 dB波束宽度)/36°(6 dB波束宽度)。这里,每个接收站的总波束数为4×1,对应的信号处理通道数为4,每组接收天线增益约14 dB,其他系统参数同表 1。
|
Download:
|
|
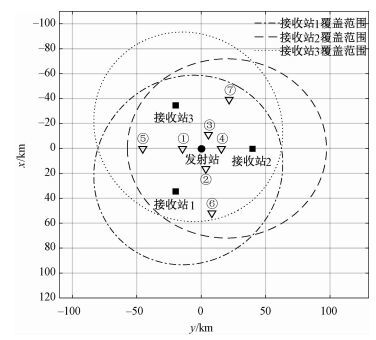
图 5 单源三站平面布局及覆盖范围 Fig. 5 Layout and coverage area of passive radar system of SITO |
|
在上述单源三站系统中,每个接收站的最大作用距离及覆盖范围的计算方法同单源单站。基于单源三站系统参数,对于每个接收站有Rrmax=98 km,Rrmin=58 km,三站覆盖范围约为30 172 km2,如图 5所示。显然单源三站的覆盖范围略优于单源单站的覆盖范围。图 5中每个椭圆的覆盖区为目标可探测区,根据每个接收站的目标回波信息可测量目标的双基距离。利用3个接收站获得的双基距离通过共视区数据关联处理后,通过解目标定位方程,即可实现目标定位,同时包括目标一定的高度信息,无需对目标进行单站测角。
3.3 单源三站目标位置测量精度假设目标到接收站1、2、3的双基距离分别为R1、R2、R3,根据辐射源、接收站及目标的位置关系有
| $\begin{array}{l} \sqrt {{x^2} + {{\left( {y - a} \right)}^2} + {z^2}} + \\ {\rm{ }}\quad \sqrt {{{(x - {x_1})}^2} + {{(y - {y_1})}^2} + {z^2}} = {R_1},\\ \sqrt {{x^2} + {{\left( {y - a} \right)}^2} + {z^2}} + \\ {\rm{ }}\quad \sqrt {{x^2} + {{\left( {y - b} \right)}^2} + {z^2}} = {R_2},\\ \sqrt {{x^2} + {{\left( {y - a} \right)}^2} + {z^2}} + \\ {\rm{ }}\quad {\rm{ }}\sqrt {{{\left( {x - c} \right)}^2} + {y^2} + {z^2}} = {R_3}. \end{array}$ | (10) |
根据式(10) 可得到x、y、z关于双基距离的表达式,
| $\begin{array}{l} x = \frac{{({K_1}{R_2} - {K_2}{R_1}){\rm{ }}{N_2} - ({K_3}{R_2} - {K_2}{R_3}){\rm{ }}{N_1}}}{{2(c{N_1} - {x_1}{N_2}){\rm{ }}{R_2}}},\\ y = \frac{{c{\rm{ }}({K_1}{R_2} - {K_2}{R_1}) - {x_1}({K_3}{R_2} - {K_2}{R_3})}}{{c{N_1} - {x_1}{N_2}}}{\rm{ }},\\ z = \sqrt {{{\left[ {\frac{{{K_2} + 2\left( {b - a} \right){\rm{ }}y}}{{2{R_2}}}} \right]}^2} - {x^2} - {{\left( {y - a} \right)}^2}} . \end{array}$ | (11) |
这里,
| $\begin{array}{l} \quad {K_1} = {R_1}^2 + {a^2} - {x_1}^2 - {y_1}^2,\\ \quad \quad {K_2} = {R_2}^2 + {a^2} - b,\\ \quad \quad {K_3} = {R_3}^2 + {a^2} - {c^2},\\ {N_1} = 2\left( {b - a} \right){\rm{ }}{R_1} - 2({y_1} - a){\rm{ }}{R_2},\\ \quad {N_2} = 2\left( {b - a} \right){\rm{ }}{R_3} + 2a{R_2} \end{array}$ |
进而根据全微分方程求得目标的位置精度,
| $\left\{ \begin{array}{l} {\rm{d}}x = \left| {\frac{{\partial x}}{{\partial {R_1}}}} \right|{\rm{d}}{R_1} + \left| {\frac{{\partial x}}{{\partial {R_2}}}} \right|{\rm{d}}{R_2} + \left| {\frac{{\partial x}}{{\partial {R_3}}}} \right|{\rm{d}}{R_3},\\ {\rm{d}}y = \left| {\frac{{\partial y}}{{\partial {R_1}}}} \right|{\rm{d}}{R_1} + \left| {\frac{{\partial y}}{{\partial {R_2}}}} \right|{\rm{d}}{R_2} + \left| {\frac{{\partial y}}{{\partial {R_3}}}} \right|{\rm{d}}{R_3},\\ {\rm{d}}z = \left| {\frac{{\partial z}}{{\partial {R_1}}}} \right|{\rm{d}}{R_1} + \left| {\frac{{\partial z}}{{\partial {R_2}}}} \right|{\rm{d}}{R_2} + \left| {\frac{{\partial z}}{{\partial {R_3}}}} \right|{\rm{d}}{R_3}. \end{array} \right.$ | (12) |
式(12) 给出目标位置精度表达式,据此可分析不同参数下的目标定位精度。表 3给出几组典型参数下的目标位置测量精度分析结果,表中仰角对应于发射站。这里先确定双基距离,然后求解目标在直角坐标系中对应的位置。
|
|
表 3 单源三站目标位置测量精度仿真结果 Table 3 Measurement accuracy simulation results of target location in SITO |
从表 3的仿真结果可以看出,在单源三站条件下基于双基距离,目标在x、y方向上的位置测量精度约200 m。在此条件下,系统虽具有一定的目标高度测量能力,但其测高误差与目标仰角成反比。
与单源单站工作方式相比,利用单源三站可以对目标在x、y方向在原理上实现较高精度定位,但由于存在三站共视区、三站目标数据空时同步和关联等问题,实际的目标定位测量精度可能比上述仿真结果低,而且三站共视区要比三站覆盖范围小。由于该定位方法是基于同时交汇探测,要求系统对目标具有较高的发现概率并正确关联。
3.4 单源三站目标速度测量精度数字电视信号频率较高,故其目标径向速度测量精度较高,而三站观测结构具有求解目标速度矢量的可能,相关研究对多目标航迹生成具有意义。
在收发分置观测结构下,将目标径向速度方向定义在收发双基地角平分线上。设目标到接收站1、2、3的径向速度分别为v1、v2、v3;直角坐标系下目标速度矢量在3个方向的分量分别为vx、vy、vz。目标位置坐标为pta=[x y z]T,发射站位置坐标为ptr=[0 a 0]T,接收站1位置坐标为pr1=[x1y10]T,接收站2位置坐标为pr2=[0 b 0]T,接收站3位置坐标为pr3=[c 0 0]T。接收站1、2、3的双基地角平分线矢量分别为
| $\begin{array}{l} {\mathit{\boldsymbol{a}}_{{\rm{t1}}}} = \frac{{{\mathit{\boldsymbol{p}}_{{\rm{r1}}}} - {\mathit{\boldsymbol{p}}_{{\rm{ta}}}}}}{{\left| {{\mathit{\boldsymbol{p}}_{{\rm{r1}}}} - {\mathit{\boldsymbol{p}}_{{\rm{ta}}}}} \right|}} + \frac{{{\mathit{\boldsymbol{p}}_{{\rm{tr}}}} - {\mathit{\boldsymbol{p}}_{{\rm{ta}}}}}}{{\left| {{\mathit{\boldsymbol{p}}_{{\rm{tr}}}} - {\mathit{\boldsymbol{p}}_{{\rm{ta}}}}} \right|}},\\ {\mathit{\boldsymbol{a}}_{{\rm{t2}}}} = \frac{{{\mathit{\boldsymbol{p}}_{{\rm{r2}}}} - {\mathit{\boldsymbol{p}}_{{\rm{ta}}}}}}{{\left| {{\mathit{\boldsymbol{p}}_{{\rm{r2}}}} - {\mathit{\boldsymbol{p}}_{{\rm{ta}}}}} \right|}} + \frac{{{\mathit{\boldsymbol{p}}_{{\rm{tr}}}} - {\mathit{\boldsymbol{p}}_{{\rm{ta}}}}}}{{\left| {{\mathit{\boldsymbol{p}}_{{\rm{tr}}}} - {\mathit{\boldsymbol{p}}_{{\rm{ta}}}}} \right|}},\\ {\mathit{\boldsymbol{a}}_{{\rm{t3}}}} = \frac{{{\mathit{\boldsymbol{p}}_{{\rm{r3}}}} - {\mathit{\boldsymbol{p}}_{{\rm{ta}}}}}}{{\left| {{\mathit{\boldsymbol{p}}_{{\rm{r3}}}} - {\mathit{\boldsymbol{p}}_{{\rm{ta}}}}} \right|}} + \frac{{{\mathit{\boldsymbol{p}}_{{\rm{tr}}}} - {\mathit{\boldsymbol{p}}_{{\rm{ta}}}}}}{{\left| {{\mathit{\boldsymbol{p}}_{{\rm{tr}}}} - {\mathit{\boldsymbol{p}}_{{\rm{ta}}}}} \right|}}。\end{array}$ |
令A=[at1at2at3]T,
Y=[vxvyvz]T,
B=[at1v1at2v2at3v3]T,
则根据速度投影关系有
| $\mathit{\boldsymbol{AY}} = \mathit{\boldsymbol{B}}$ | (13) |
即
| $\mathit{\boldsymbol{Y}} = {\mathit{\boldsymbol{A}}^{ - 1}}\mathit{\boldsymbol{B}}.$ | (14) |
式(14) 表明只要目标位置矩阵可逆,其直角坐标系速度矢量就可求解。
另外,令
| $\mathit{\boldsymbol{D}} = {\mathit{\boldsymbol{A}}^{ - 1}}\mathit{\boldsymbol{E}}.$ | (15) |
其中:A、E均为只与目标位置及系统布局有关的矩阵,所以式(15) 说明直角坐标系下速度矢量对径向速度的偏导矩阵只与目标位置及系统布局有关。
令直角坐标系下的速度精度矢量为dY=[dvx dvy dvz]T,径向速度精度矢量为dX=[dv1 dv2 dv3]T,根据全微分方程有
| ${\rm{d}}\mathit{\boldsymbol{Y}} = {\rm{abs}}(D){\rm{d}}\mathit{\boldsymbol{X}}.$ | (16) |
目标径向速度的测量需通过3个接收站多普勒频率测量实现,故直角坐标系下的目标速度精度矢量与目标位置、系统布局和多普勒频率测量精度有关。设信号积累时间为1 s,多普勒频率分辨率为1 Hz,假设多普勒频率精度与其分辨率相当,则根据多普勒频率精度表达式
根据式(16),即可分析直角坐标系中不同参数下目标的速度测量精度。表 4给出图 5中①、②、⑥、⑦ 所示位置目标的速度测量精度分析结果。仿真中假定直角坐标系下目标高度向速度为零,即速度矢量位于xy平面,同时给出与之对应3个接收站的径向速度。
|
|
表 4 单源三站目标速度测量精度仿真结果 Table 4 Measurement accuracy simulation results of target velocity in SITO |
从表 4的仿真结果可以看出,在单源三站条件下基于径向速度,可在直角坐标系下对目标进行速度矢量测量,x、y方向的速度测量精度约1 m/s,与x、y方向相比z方向的速度测量精度较差,其测量误差与目标仰角成反比。
4 结束语基于数字电视信号的外辐射源雷达目前得到广泛的关注和研究,本文论述其主要问题及系统性能损失,同时以单源单站和单源三站为例对其空中目标探测性能进行分析。研究结果表明,当覆盖范围约为30 000 km2,在接收天线均使用96个阵元的情况下,单源单站需要总波束数为4×5,对应的信号处理通道数为20,单源三站需要总波束数为3×4×1,对应的信号处理通道数为12。
单源多站组网方式可降低系统的复杂度,在实现目标探测和定位的同时也可实现直角坐标系中的速度矢量测量,有助于改善目标航迹质量,将是未来发展的一个重要趋势。
| [1] | 苏卫民, 顾红, 张先义. 基于外辐射源的雷达目标探测与跟踪技术研究[J]. 现代雷达, 2005, 27(4):19–22. |
| [2] | 李红伟. 外辐射源雷达目标定位与跟踪方法研究[D]. 西安: 西安电子科技大学, 2012. |
| [3] | Wang Y S, Bao Q L, Wang D H, et al. An experimental study of passive bistatic radar using uncooperative radar as a transmitter[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(9):1868–1872. DOI:10.1109/LGRS.2015.2432574 |
| [4] | Colone F, Cardinali R, Lombardo P, et al. Space-time constant modulus algorithm for multipath removal on the reference signal exploited by passive bistatic radar[J]. IET Radar, Sonar & Navigation, 2009, 3(3):253–264. |
| [5] | Baczyk M K, Malanowski M. Decoding and reconstruction of reference DVB-T signal in passive radar systems[C]//The 11th International Radar Symposium(IRS), Vilnius, Lithuania, 2010: 1-4. |
| [6] | O'Hagan D W, Kuschel H, Heckenbach J, et al. Signal reconstruction as an effective means of detecting targets in a DAB-based PBR[C]//International Radar Symposium, Vilnius, Lithuania, 2010: 48-51. |
| [7] | 张瑜, 贺秋瑞. 无源雷达探测中的直达波提取方法[J]. 舰船科学技术, 2013, 35(3):74–77. |
| [8] | 郗莹, 李道京. 成像雷达微弱运动目标信号AD采样问题分析[C]//第四届微波遥感技术研讨会, 延吉, 2015: 100-103. |
| [9] | 赵耀东. UHF波段无源雷达信号处理算法研究[D]. 北京: 中国科学院大学, 2013. http://159.226.65.12/handle/80137/9909 |
| [10] | 纪传, 吕晓德, 向茂生, 等. 等效凹槽滤波器及其在无源相关定位雷达中的应用[J]. 雷达学报, 2014, 3(6):675–683. |
| [11] | 冯远. 数字电视辐射源雷达参考信号获取及干扰抑制算法研究[D]. 北京: 北京理工大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10007-1015029489.htm |
| [12] | 关欣, 胡东辉, 仲利华, 等. 一种高效的外辐射源雷达高径向速度目标实时检测方法[J]. 电子与信息学报, 2013, 35(3):581–588. |
| [13] | 李道京, 刘波, 尹建凤, 等. 高分辨率雷达运动目标成像探测技术[M]. 北京: 国防工业出版社, 2014. |
| [14] | Joachim Ender. A compressive sensing approach to the fusion of PCL sensors[C]//The second International Workshop on Compressed Sensing appllied to Radar(CoSeRa 2013), Bonn, Germany, 2013: 100-110. |
| [15] | 赵洪立, 习建博. 一种基于多辐射源匹配的未知辐射源的定位方法[J]. 雷达学报, 2014, 3(6):727–730. |
| [16] | 鄢社锋, 马远良. 传感器阵列波束优化设计及应用[M]. 北京: 科学出版社, 2009. |
| [17] | Van Trees H L. Optimum array processing: Part Ⅳ of detection, estimation, and modulation theory[M]. New York: John Wiley & Sons, Inc, 2002. |
| [18] | Merrill I, Skolin. 雷达手册[M]. 王军, 林强, 等译. 北京: 电子工业出版社, 2003. |
 2017, Vol. 34
2017, Vol. 34 


