According to Shannon's source-channel separation theory[1], source coding, channel coding, information security, and modulation can be performed separately and sequentially for any typical communication system, while maintaining optimality for the communication transmission. In particular, source encoder and decoder can be designed without knowing the channel state information (CSI). Although the separation theorem, which is true for considerable classes of sources and channels, does not always hold, the separation approach has been widely adopted in practical communication systems due to the great reduction in complexity.
Source coding is used to improve the efficiency of transmission by compressing information data. Channel coding is provided for correcting channel errors by adding some check bits and for ensuring the reliability of data. Information security is responsible for ensuring data security transmission. Modulation improves the bandwidth efficiency of communication transmission under conditions of limited power and bandwidth constraints[2-3].
However, practical communication systems are constrained by delay, bandwidth, and power, and do not satisfy the assumptions of Shannon's separation theory. On the other hand, the performance of a wireless communication system is also greatly influenced by the knowledge of the CSI at the transmitter side (CSIT) and at the receiver side (CSIR). Here, CSI refers to the knowledge about the actual status of the wireless channel. CSI plays an important role in many sophisticated transmission techniques such as linear precoding and beamforming. In both theory and practice, (relatively) accurate CSIR can be measured by sending training sequences known a priori to the receiver whereas CSIT is usually obtained via feedback. However, due to practical limitations such as link capacity and delay constraint, obtaining arbitrarily accurate feedback information is often infeasible in most wireless systems. Furthermore, it is known that Shannon's source-channel separation theorem does not hold when full CSIT is not available[4-5]. Therefore, to achieve an optimal performance, joint source-channel transmission approaches are in general required. The cross-layer wireless network design approach addresses this issue by jointly optimizing the allocation of network resources such as power and bandwidth based on the wireless channel conditions and the quality of service (QoS) requirement[6]. Driven by the increasing demands for reliable universal connectivity, higher throughput, and wireless applications with stringent delay and energy constraints such as wireless broadband multimedia services, future wireless systems must employ advanced algorithms and techniques to offer better reliability and higher data rate. However, as we have already seen, while rapid progresses have been made, wireless system performance is still limited due to the many challenging issues mentioned above. This prompts us to study the fundamental performance limitations of wireless communication systems, which will provide us a complete picture and some useful insights into this intricate problem, in particular, the joint impact of key factors such as fading, user cooperation, and CSI feedback on the system performance[7-8]. Furthermore, as we take into consideration both the source and channel characteristics in the joint source-channel system design, it is also important to adopt an appropriate measure that characterizes the end-to-end performance of the overall system. In recent years, joint en/decoding approaches attracted extensive attention in academic circles, including joint source channel en/decoding approaches and joint source channel symbol-level en/decoding approaches[9-12]. Due to the perfect performance at low signal to noise ratio (SNR) levels, turbo codes have entered into service in many communication applications such as CCSDS standards, etc. Naturally, the new subject of JSCD for the VLC combined with a turbo code attracted increasing research interests. A model of iterative decoding between two SISO modules based on a bit-level super trellis was proposed by Laković and Villasenor[13].
A Joint source channel symbol-level en/decoding fast algorithm based on the space policy trellis for the variable-length symbol-A posteriori probability (VLS-APP) decoding is proposed in this work. We construct a new efficient space policy trellis by introducing and optimizing the weight value of variable-length symbols under condition of meeting the constraint equation of decoding, and achieve a low-complexity joint source channel symbol-level decoding with the VLS-APP algorithm. Simulation result shows that symbol-level decoding with this space policy trellis has better performance than the symbol-level decoding with other plane trellis or the separation bit-level decoding with a posteriori probability (APP) algorithm. It is obvious that the symbol-level decoding with our space policy trellis achieves the best decoding performance among all the methods.
1 Joint source channel symbol-level en/decoding system 1.1 Separate source and channel codingThe source-channel separation theorem indicates that several parts in a communication system can be designed independently. In the source coding stage of the separate source and channel coding system, a discrete-time source {s1, s2, …, sK} with K samples (e.g., image, video, or speech signal) is mapped to an index (message) w drawn from a finite alphabet W={1, 2, …, M}. It is clear that on average each source sample is represented by
In the channel coding stage, the message w is mapped into a sequence of N channel symbols {x1, x2, …, xN} to be transmitted over the channel, for which we say the communication consumes N channel uses. {x1, x2, …, xN} is referred to as a length-N codeword. The set of all codewords is called a codebook, which should be known well in the communication system. Since the communication system attempts to transmit log2M bits of information through the channel after N channel uses, the rate of the channel code is thus
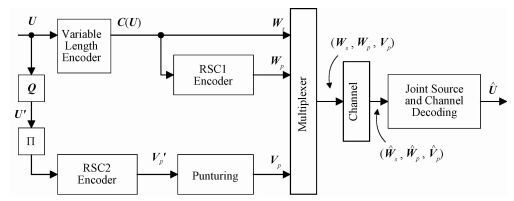
Joint source channel en/decoding model for the transmission system is depicted in Fig. 1. In the encoding part, the variable-length coding (VLC) is first integrated with the upper recursive systematic convolutional (RSC) code of a turbo code into a single component code. We assume that the VLC is prepared for a source symbol sequence U=[U1, U2, …, UK] with K symbols, where each Uk(k=1, 2, …, K) from a finite source set must be encoded to a variable-length codeword symbol c (Uk). So a coded symbol sequence C (U)=[c (U1), c (U2), …, c (UK)] composed of K variable length codewords can be obtained through the VL encoder, and then can be expressed as a binary sequence ws=[ws1, ws2, …, wsn1] with the total bits length n1. The channel RSC1 encoder provides a parity check sequence wp=[wp1, wp2, …, wpn1] in order to increase the robustness of the sensitive variable-length bit stream ws. By utilizing a Q-bit quantization process, the source symbol sequence U is converted into a bit sequence U′=[U′1, U′2, …, U′K] with quantized bits u′k=[u′k1, u′k1, …, u′kQ](k=1, 2, …, K). Then the bit sequence U′ is permuted by the bit-level interleaver ∏ and coded by another channel encoder RSC2[9, 12-13].
|
Download:
|
|
Fig. 1 Joint source-channel en/decoding model for the transmission system |
|
We assume that coherently detected binary phase-shift keying (BPSK) modulation and signals are transmitted over an additive white Gaussian noise (AWGN) channel. After the channel observations are received, an iterative JSCD is carried out in order to obtain the output as

|
Download:
|
|
Fig. 2 Iterative source-channel decoding model for the transmission system |
|
In order to get the symbol-level output of the posteriori probability, two kinds of side information based on a plane trellis is proposed and used in Ref. [8-9, 11], and then the corresponding BCJR algorithm is applied to the logarithm likelihood ratios (LLRs). The symbol level a posteriori probability (APP) for each symbol ck at the moment k can be calculated by using formula (1). Given the observation sequence R1M from the channel, the posteriori probability of symbol ck is
| $\begin{array}{l} P{\rm{ }}({c_k} = c{\rm{ }}\left( i \right)/\mathit{\boldsymbol{R}}_1^M) = \sum\limits_{t \in {\Re _k}} {} \sum\limits_{t\prime \in {\Re _{k - 1}}} {} P{\rm{ }}({T_k} = t,{c_k} = c{\rm{ }}\left( i \right),\\ {T_{k - 1}} = t\prime /\mathit{\boldsymbol{R}}_1^M) = \xi \cdot \sum\limits_{t \in {R_k}} {} \sum\limits_{t\prime \in {R_{k - 1}}} {} \underbrace {p{\rm{ }}({T_{k - 1}} = t\prime ,\mathit{\boldsymbol{R}}_1^{m{\rm{ }}(t\prime )})}_{{\alpha _{k - 1}}\left( {t\prime } \right)}\cdot\\ \quad \quad \quad \quad \quad \quad \underbrace {p{\rm{ }}(\mathit{\boldsymbol{R}}_{m{\rm{ }}\left( t \right) + 1}^M/{T_k} = t)}_{{\beta _k}\left( t \right)} \cdot \\ \quad \quad \underbrace {p{\rm{ }}(\mathit{\boldsymbol{R}}_{m{\rm{ }}\left( {t\prime } \right) + 1}^{m{\rm{ }}(t)},{c_k} = c{\rm{ }}\left( i \right),{T_k} = t/{T_{k - 1}} = t\prime )}_{{\gamma _k}^i(R_{m{\rm{ }}\left( {t\prime } \right) + 1}^{m{\rm{ }}(t)},t\prime ,t)}, \end{array}$ | (1) |
where ξ=1/R1M is a constant usually. In formula (1), the first probability αk(t) is defined as the forward recursive factor that can be calculated by a forward iteration, and the probability βk(t) is similarly defined as the backward recursive factor that can be obtained through a backward iteration. The last probability γki(Ym (t′)+1m (t), t′, t) is the transition probability from the state Tk-1=t′ to Tk=t and associated with the situation of ck=c (i), where c (i) is an input symbol[3, 11].
However, the structure of a plane trellis is complicated, and it contains lots of competence paths for the decoding. So the computational complexity of the symbol-level APP decoding algorithm based on a plane trellis will increase as a square level with the growth of decoding symbols. The methods presented in Refs.[9] and [14] proposed that competence paths could be eliminated by introducing a new side information of accumulated weight value of the decoded symbols. However, without optimizing the weight value of variable length symbols, the decoding complexity in those methods was still high.
2 The fast en/decoding algorithm based on the optimized design of space policy trellisBased on the above analysis in section 1, we propose a new joint source channel symbol-level en/decoding fast algorithm using an optimized space policy trellis.
For a source set X={x1, x2, …, xM}, which contains M variable-length symbols, the corresponding probability distribution and the symbol length are {p (x1), p (x2), …, p (xM)} and {l (x1), l (x2), …, l (xM)} respectively. The length of the decoding symbol sequence is K.
For the process of joint source channel symbol-level decoding based on the space policy trellis, any possible decoding paths should satisfy three conditions of side information as follows. Both the total number of decoded bits as L-allbits and the total number of decoded symbols K are certain, and at same time the accumulated weight value of decoded symbols as φ-allbits is also fixed. These three constraints are expressed as:
| $\begin{align} & K=\sum\limits_{i=1}^{M}{{}}{{n}_{i}}, \\ & L-\text{allbits}=\sum\limits_{i=1}^{M}{{}}l\text{ }({{x}_{i}})\cdot {{n}_{i}}, \\ & \varphi -\text{allbits}=\sum\limits_{i=1}^{M}{{}}{{{\tilde{\varphi }}}_{i}}\cdot {{n}_{i}}, \\ \end{align}$ | (2) |
where ni represents the total number of the i-th variable length symbol in a decoding path, and
For the decoding fast algorithm based on a space policy trellis, it is crucial to optimize the side information of accumulated weight value of the decoding path. Under the consideration of using the probability difference and the length characteristic of each variable length symbol, we suggest construction of the weigh values of M variable length symbols in a way given below.
For any variable length coding, the length of symbol with high probability is short. Similarly, we hope that the difference for each weight value is associated with the probability of variable length symbols. We let
| ${{{\tilde{\varphi }}}_{i}}=\left\lfloor {{{\tilde{\varphi }}}_{i-1}}-\ln \frac{p\text{ }({{x}_{i}})}{p\text{ }({{x}_{i-1}})}\text{ }\times l\text{ }({{x}_{i}}) \right\rfloor .$ | (3) |
Then each weight value
Then the space policy trellis for decoding is constructed by using the optimized weight values {
|
Download:
|
|
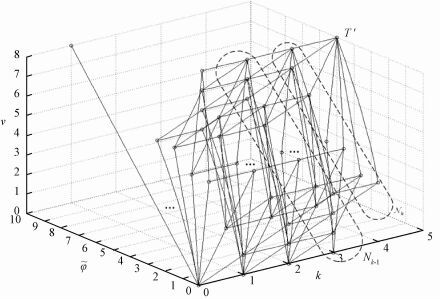
Fig. 3 VLC space policy trellis |
|
It can be seen that the variable-length symbols C={c (x1), c (x2), …, c (xM)} mapped from the source set X will be transmitted over the channel and every possible variable-length code word of the corresponding decoding sequence U=[u1, u2, …, uK] will exist on the space policy trellis (as illustrated in Fig. 4).
|
Download:
|
|
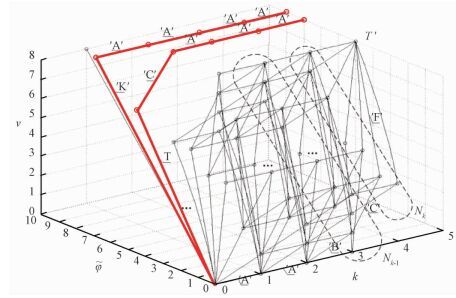
Fig. 4 VLC space policy trellis and elimination of two red paths |
|
As shown in Fig. 4, three decoding paths can reach the state where the number of decoded symbol is 5 and the number of accumulated decoded bits is 8. However, the two red paths can be eliminated because the accumulated weight value exceeds φ-allbits (=5) for that source variable length symbol sequence.
So on the basis of the space police trellis with the optimized weigh values of variable length symbols, the joint decoding process first computes the optimum decoding path constrained by the equations in formulae (2) and the space policy trellis with optimized weight values.
The second step of the joint decoding process is that the state node and the state transfer branch of the space policy trellis are projected to a 2-D plane composed of "the symbol number index k" and "the bit state index v". This generates a simplified plane trellis named as the VLC KV space policy trellis and at the same time still keeps the transfer relationship between the state nodes in the space policy trellis.
Further, the VLC KV policy trellis can be extended to construct a variable-length symbol-level joint policy trellis with complex states, which is applied for joint source channel decoding using the VLS-APP algorithm. This specific process is the same as that in Ref. [11]. The complexity of the VLC directly affects the computation amount of the VLS-APP algorithm. The simplified VLC KV plane trellis has a lower complexity, which reduces the computation amount of the VLS-APP algorithm and, as a result, the decoding process is speeded.
3 Simulation results and analysisThe experiments were carried out over the AWGN channel modulated with BPSK in order to evaluate the performance of the proposed joint source channel symbol-level coding/decoding approach based on space policy trellis. We have performed two simulation experiments and compared the proposed joint source channel symbol-level approach based on space policy trellis with existing bit-level separate approaches[13] based on plane trellis[8-9]. All simulation experiments were carried out over the multiple simulation platform of joint source channel encoding and decoding developed by Visual C++.
3.1 Comparison of decoding complexity with plane trellisIn order to verify that the fast algorithm proposed in this work reduces the complexity of decoding efficiently, we compare the decoding time of different numbers of source reversible variable symbols using reversible variable length codes (RVLC) in Refs.[14-16]. The same code-table of RVLC as in Ref. [14] with the pre-statistical length L is set to 12, which means that the length of continuous string "0" or string "1" is from 1 to 12. In the case of 12-RVLC source-symbol, its parameters is listed in Table 1, the decoding symbol length K=10, the interleaver length N=600 bits, and the decoding iteration times=8. The last column in table 1 shows the optimum weigh value
|
|
Table 1 Parameters of 12-RVLC source-symbol |
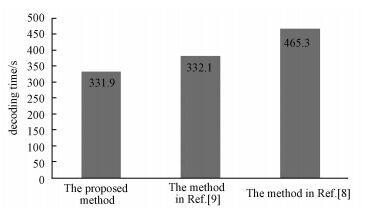
Simulation results are illustrated in Fig. 5. It is shown that the decoding time of the proposed method with the new efficient space policy trellis reduces by about 49.3% and 39.4%, compared with the method with plane trellis in Refs.[8-9], respectively. We calculated the total number of all possible branch paths in these three decoding processes, and found that the proposed method with the new efficient space policy trellis under condition of the optimized
|
Download:
|
|
Fig. 5 Decoding time comparison among different methods |
|
To compare the decoding performance of 12-RVLC source-symbols with bit-level separate system and plane trellis, two simulation experiments were carried out. In the case of 12-RVLC source-symbol (its parameters are listed in Table 1), the decoding symbol length K=10 under the condition of 8 iterations and the decoding symbol length K=16 under the condition of 16 iterations. The interleaver lengths in these two situations are both 600 bits. The total number of the source symbol sequence is 180 000.
The purpose of the two simulations is to show the performance of Eb/N0 (the signal to noise ratio, determined by signal power par bit and noise power spectral density) under the condition of the same bit error rate (BER). We compare the joint decoding performance of our joint source channel symbol-level en/decoding fast algorithm based on the space policy trellis with the optimum weight values with the performances of the same joint en/decoding algorithm based on the plane trellis in Ref. [8] and the separate en/decoding method with bit-level a posteriori probability (APP) algorithm in Ref. [13].
In Fig. 6 shown are the BER vs. Eb/N0 performance curves of those three methods mentioned above, under conditions of the decoding symbol length K=10 and 8 iterations. Generally speaking, the decoding performance of our method proposed in this work is the best. At BER=2×10-5, the signal to noise gain of VLS-APP decoding based on the space policy trellis with optimum weight values in this work is 1.3 dB in comparison with the joint source channel symbol-level decoding with plane trellis in Ref. [8]. At the same time, an Eb/N0 gain of about 1.7 dB is obtained by the proposed method in this work, compared to the separate en/decoding methods with bit-level APP algorithm in Ref. [13].

|
Download:
|
|
Fig. 6 BER performance comparison among three methods (with 8 iterations) |
|
We investigate the decoding performance of those three methods in the situation of a greater decoding complexity. So we increase the decoding symbol length K from 10 to 16, and the times of iteration from 8 to 12, but keep the interleaver length of 600 bits. The result of simulation is shown in Fig. 7, which indicates that our method still performs best when the demand of decoding becomes more complicated. A BER=2×10-5, the joint source channel en/decoding fast algorithm in this work gains Eb/N0 by about 1 dB and 1.8 dB, compared to the method with plane trellis in Ref. [8] and the separation en/decoding method in Ref. [13].
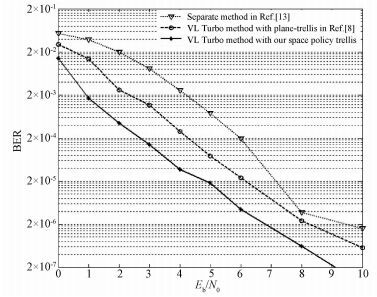
|
Download:
|
|
Fig. 7 BER performance comparison among three methods (with 12 iterations) |
|
On the basis of the construction of a new efficient space policy trellis by optimizing the weight value of variable-length symbols, a fast decoding method with VLS-APP algorithm is presented in this paper, which can be used for joint source channel symbol-level encoding and decoding. The space policy trellis proposed in this work is helpful to eliminate competitive decoding path in an efficient way, and obviously reduces the complexity of iterative decoding for a joint source channel symbol-level communication system. The results of simulations on both decoding complexity and transmission performance show that symbol-level decoding with the new efficient space policy trellis performs better than that with other plane trellis and the separate bit-level decoding method with APP algorithm. This method could be well used in resource-constrained environment such as the space communication scene.
| [1] | Shannon C E. A mathematical theory of communication[J]. Bell System Technical Journal, 1948, 27(3):3–55. |
| [2] | Chen C, Tu G F, Zhang C. Joint source-channel coded multidimensional modulation for variable-length codes[J]. Science China Information Sciences, 2014, 57(6):1–12. |
| [3] | Proakis J G, Salehi M. Digital communication[M].5th ed. New York: McGraw-Hill Education, 2007. |
| [4] | Cover T M, Thomas J A. Elements of information theory[M].2nd ed. New York: Wiley, 2006. |
| [5] | Tu G F, Liu J J, Zhang C, et al. Studies and advances on joint source-channel encoding/decoding techniques in flow media communications.[J]. Science China Information Sciences, 2010, 53(1):1–17. DOI:10.1007/s11432-010-0001-4 |
| [6] | Tu G F, Zhang C, Nimann H, et al. Scalable video object coding & QoS control for next generation space internet[J]. Science in China, 2008, 51(5):599–608. |
| [7] | Cheng C, Tu G F, Zhang C, et al. Optimization of irregular mapping for error floor removed bit-interleaved coded modulation with iterative decoding and 8PSK[J]. EURASIP Journal on Wireless Communications & Networking, 2014, 2014(1):217–232. |
| [8] | Liu J, Tu G F, Zhang C, et al. Joint source and channel decoding for variable length encoded turbo codes[J]. EURASIP Journal on Advances in Signal Processing, 2007, 2008(1):1–7. |
| [9] | Chen S H, Zhang C, Tu G F, et al. Low-complexity joint source-channel decoding based on variable length encoded Turbo codes[J]. Journal of the Graduate School of the Chinese Academy of Sciences, 2011, 28(2):246–252. |
| [10] | Wang J. Cooperation and joint source-channel transmission in wireless networks[D]. Burnaby: Simon Fraser University, 2010. |
| [11] | Tu G F, Liu J J, Zhang C, et al. Joint source-channel en/decoding based on a new symbol-level joint trellis[J]. Chinese Journal of Electronics, 2011, 20(1):114–120. |
| [12] | Liu J J, Tu G F, Wu W R. New iterative super-trellis decoding with source a priori information for VLCs with turbo codes[J]. Journal of Electronics, 2007, 24(1):122–127. |
| [13] | Laković K, Villasenor J. Combining variable length codes and turbo codes[C]//IEEE 55th Vehicular Technology Conference, 2002: 1 719-1 723. |
| [14] | Huo Y H, Zhang C, Gao S S. Low-complexity joint source-channel coding and decoding approach based on space trellis[J]. Journal of Graduate School of Chinese Academy of Sciences, 2012, 29(4):493–500. |
| [15] | Tu G F, Liu X M, Zhang C, et al. Joint source-channel coding/decoding by combining RVLC and VLC for CCSDS IDC coefficients[C]//IEEE International Conference on Networking, Sensing and Control, 2010: 49-52. |
| [16] | Chen C, Tu G F, Zhang C. Joint source-channel coded multidimensional modulation for variable-length codes[J]. Science China Information Sciences, 2014, 57(6):1–12. |
 2017, Vol. 34
2017, Vol. 34 


