2. 中国矿业大学信息与控制工程学院, 江苏 徐州 221116;
3. 中国科学院大学, 北京 100049
2. School of Information and Control Engineering, China University of Mining and Technology, Xuzhou 221116, Jiangsu, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
图像在采集、压缩、处理和传输的过程中经常会引入各种类型的失真,如块效应、模糊、噪声等。图像失真的大小决定图像质量的高低,也决定图像处理方法的性能优劣,因此研究图像的质量评价具有很重要的意义。图像质量评价方法通常分为主观评价方法和客观评价方法两大类。主观评价方法一般是由人眼直接观察并评价图像质量,最终统计其评价结果;客观评价方法是设计算法提取图像的失真信息,并综合这些信息得到图像的质量分数。主观评价方法更符合人的视觉感知特性,是最为准确、可靠的图像质量评价方法,但是由于容易受到评价环境及观察者经验水平、个人偏好等外界不确定因素的影响,评价结果往往不稳定,具有较强的随机性,并且成本较大,也不适用于实时系统。客观评价方法具有简单、稳定、实时等特点,但往往不能精确反映出人的视觉感知特性。由于人是图像的最终使用者,研究符合人类视觉系统 (HVS) 特性的客观质量评价方法是图像质量评价的关键问题。寻找一种能够最大程度地反映HVS特性的图像质量客观评价方法至关重要,将极大促进视频技术的发展。
根据图像质量评价方法对原始图像的依赖程度,质量评价方法一般分为3种类型,即全参考、部分参考和无参考[1]。全参考方法就是利用原始图像的所有信息,通过统计原始图像与失真图像之间的信号差异得到失真图像的质量评价结果。一般可以分为以下几类:1) 基于像素统计误差的方法,这类方法包括均方误差 (MSE) 和峰值信噪比 (PSNR),这两种方法通过计算对应像素点的像素值之间的误差衡量图像的质量,这类算法的缺点是评价结果不能很好地反映人眼对图像的主观感受。2) 基于结构相似度的算法包括结构相似性 (SSIM)[2]方法,该方法认为人眼主要功能是提取视场中的结构信息,并且人眼对视场内结构的变化具有高度的自适应性。3) 基于通用图像质量指数 (UQI)[3]方法,该方法利用图像之间互相关性以及图像亮度、对比度差异性衡量图像质量。4) 基于信息论提出的信息保真度方法,主要代表性方法为视觉信息保真度 (VIF)[4],此算法通过计算原始图像与失真图像之间的互信息度量图像质量。5) 基于人类视觉算法,如:JND模型,这种方法主要将人眼的视觉特性与视觉相似度结合起来,能够区分图像中不同区域的图像特征,得到符合人眼视觉特性的质量评价方法。部分参考方法是利用图像的特征进行质量评价。无参考方法是在没有原始图像的条件下进行质量评价的一种方法。本文的研究工作是基于全参考帧的质量评价方法。
基于图像全参考的质量评价方法的研究工作很多,文献[5]提出一种基于离散正交矩的图像质量评价方法,是众多方法中性能突出的方法之一。该方法是基于图像块的质量评价方法,将图像划分成图像块,然后计算各个图像块的离散正交矩的矩变换矩阵,并利用参考图像和测试图像对应的矩变换矩阵相关系数计算图像块的质量分数。所以正交矩能够很好地提取图像特征,对图像进行质量评价。文献[5]的方法中利用离散正交矩计算的图像块矩的变换矩阵中的值不一定是正值,所以直接使用参考图像和测试图像对应的矩变换矩阵相关系数作为图像块的质量分数不合适,应该计算矩变换矩阵的矩能量差异以求得图像块的质量分数。
文献[5]的方法使用了Tchebichef矩[6]和Krawtchouk矩[7]的离散正交矩方法。尽管离散正交矩运算性能相比其他方法有一定的优势,但连续正交矩也有自己的优点。Gaussian-Hermite矩作为一种连续正交矩,比离散正交矩方法有更好的图像重建效果[8],可以很好地提取图像的特征信息,又因为客观质量评价方法需要正确反映人的主观感受,所以本文采用连续正交矩Gaussian-Hermite和人类视觉系统的掩盖效应对图像进行质量评价,可以与主观评价方法保持很好的一致性,能够准确衡量图像的质量。
1 Gaussian-Hermite矩Gaussian-Hermite矩理论上的定义区间为 (-∞, +∞),为了计算大小为K×K数字图像I(i, j) 的矩变换矩阵,我们把Gaussian-Hermite矩的核函数Hp(x/σ) 转换成离散核函数
| $ \begin{array}{l} {{\tilde H}_p}\left( {i, K;\sigma } \right) = {\left[{{2^p}p!\sqrt {\pi } }\sigma \right]^{ -1/2}} {\cdot} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{exp}}( -{X^2}/2{\sigma ^2}){H_p}\left( {X/\sigma } \right), \end{array} $ | (1) |
式 (1) 即为Gaussian-Hermite矩核函数的离散形式,图像的矩变换矩阵可以通过式 (2) 得到:
| $ {\eta _{pq}} = \frac{4}{{{{\left( {K-1} \right)}^2}}}\sum\limits_{i = 0}^{K-1} {\sum\limits_{j = 0}^{K-1} I } \left( {i, j} \right){{\tilde H}_p}\left( {i, K;\sigma } \right){\cdot}{{\tilde H}_q}\left( {j, K;\sigma } \right), $ | (2) |
其中,p+q为阶数,并且p, q=0, 1, 2, …, K-1,因为正交矩的正交性,图像可以利用式 (2) 的逆运算进行重构:
| $ I\left( {i, j} \right) = \sum\limits_{p = 0}^n {\sum\limits_{q = 0}^n {{\eta _{pq}}} } {{\tilde H}_p}\left( {i, K;\sigma } \right){{\tilde H}_q}\left( {j, K;\sigma } \right). $ | (3) |
由上可知,正交矩具有正交性和不变性的特性,所以常常用来进行图像特征提取。
2 人类视觉系统掩盖效应图像的观测者是人,人眼在对图像进行评估时会根据图像不同区域的亮度和纹理复杂度有不同的侧重,所以图像质量评价不仅仅是对图像像素的简单处理,还应该考虑人类视觉系统的掩盖效应[9]。HVS的掩盖效应主要包括两种:亮度掩盖效应和纹理复杂度掩盖效应。
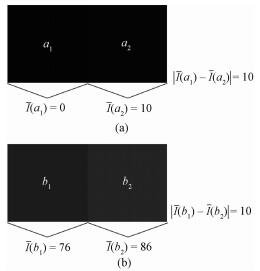
人眼对图像中不同亮度区域的关注是不同的,如图 1所示,相邻两图像块平均像素差异均为10,图 1(a)中几乎看不到两图像块的差异,但是图 1(b)中两图像块差异却很明显。
|
Download:
|
|
图 1 图像中的亮度掩盖效应示例图 Fig. 1 Brightness masking effect in image |
|
所以对于不同亮度区域的图像块应该加上亮度掩盖权值cv,假设图像块平均亮度为I,则图像块的亮度掩盖加权值cv为
| $ cv = \left\{ \begin{array}{l} {\left( {\frac{{\bar I}}{{81}}} \right)^{1/2}}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 < \bar I \le 81, \\ 1-\left( {81-\bar I} \right) \cdot \left( {\frac{{0.3}}{{174}}} \right), \;\;81 < \bar I \le 255. \end{array} \right. $ | (4) |
由式 (4) 可知,图像块平均亮度值为81时,cv值最大为1,平均亮度越大或越小,cv值越小。
图像中纹理十分复杂的区域会掩盖一些细节信息,所以人眼对图像中纹理复杂的区域不敏感。如图 2所示,在鹦鹉的眼部和头部失真情况下,人眼会更容易注意到较平坦的头部区域的失真。

|
Download:
|
|
图 2 图像中的纹理掩盖效应示例图 Fig. 2 Texture masking effect in image |
|
所以对于不同纹理区域的图像块应该分成平坦和非平坦区域图像块,假设图像块平均亮度为I,图像块每个像素为I(i, j),则纹理复杂度SSM[10]为
| $ {\rm{SSM}} = \sum\limits_{i, j = 0}^n {{{\left[{I\left( {i, j} \right)-\bar I} \right]}^2}} . $ | (5) |
如果图像块纹理复杂度SSM小于阈值TSSM,则图像块为平坦图像块;反之,图像块为非平坦图像块。根据文献[10],图像块的纹理复杂度掩盖权值ct为
| $ ct = \left\{ \begin{array}{l} 0.8, \;\;\;{T_{{\rm{SSM}}}} < 5000, \\ 0.2, \;\;\;{T_{{\rm{SSM}}}} \ge 5000. \end{array} \right. $ | (6) |
因为连续正交矩具有较好地提取图像信息的能力,所以我们利用Gaussian-Hermite矩对图像进行分块计算,然后融合人类视觉掩盖效应,针对不同区域的图像块进行加权,最后平均得到图像的质量分数。具体过程如下。
首先把参考图像和测试图像划分成不重叠的8×8的图像块,然后计算图像块的低阶矩变换矩阵,即
| $ \mathit{\boldsymbol{M}}_k^{\rm{R}} = \left( {\begin{array}{*{20}{c}} {m_{00}^{\rm{R}}} & {m_{01}^{\rm{R}}} & {m_{02}^{\rm{R}}}\\ {m_{10}^{\rm{R}}} & {m_{11}^{\rm{R}}} & {m_{12}^{\rm{R}}}\\ {m_{20}^{\rm{R}}} & {m_{21}^{\rm{R}}} & {m_{22}^{\rm{R}}} \end{array}} \right), $ | (7) |
| $ \mathit{\boldsymbol{M}}_k^{\rm{T}} = \left( {\begin{array}{*{20}{c}} {m_{00}^{\rm{T}}} & {m_{01}^{\rm{T}}} & {m_{02}^{\rm{T}}}\\ {m_{10}^{\rm{T}}} & {m_{11}^{\rm{T}}} & {m_{12}^{\rm{T}}}\\ {m_{20}^{\rm{T}}} & {m_{21}^{\rm{T}}} & {m_{22}^{\rm{T}}} \end{array}} \right). $ | (8) |
其中,MkR和MkT分别代表参考图像和测试图像的第k个图像块的矩变换矩阵。因为MkR和MkT中的值可以是非正值,所以不能直接利用MkR和MkT进行相关性运算,应该对MkR和MkT进行如下调整:
| $ {A_k} = {({a_{ij}})_{3 \times 3}} = {\rm{abs}}(\mathit{\boldsymbol{M}}_k^{\rm{R}}), $ | (9) |
| $ {B_k} = {({b_{ij}})_{3 \times 3}} = {\rm{abs}}(\mathit{\boldsymbol{M}}_k^{\rm{T}}). $ | (10) |
其中,Ak和Bk就是正交矩能量值,根据Ak和Bk,可以得到图像块的矩能量差异
| $ {T_k} = {({t_{ij}})_{3 \times 3}} = {\left( {\frac{{2{a_{ij}}{b_{ij}}}}{{{a_{ij}}^2 + {b_{ij}}^2}}} \right)_{3 \times 3}}, $ | (11) |
其中,tij∈(0, 1], i, j=0, 1, 2,然后根据图像块的亮度和纹理复杂度掩盖权值得到
| $ f({t_{ij}}) = {t_{ij}}{\cdot}cv{\cdot}ct. $ | (12) |
其中cv∈(0, 1],所以矩相关矩阵为
| $ {\mathit{\boldsymbol{I}}_k} = (f{({t_{ij}}))_{3 \times 3}} = \left( {\begin{array}{*{20}{c}} {I_{00}^{^k}} & {I_{01}^{^k}} & {I_{02}^{^k}}\\ {I_{10}^{^k}} & {I_{11}^{^k}} & {I_{12}^{^k}}\\ {I_{20}^{^k}} & {I_{21}^{^k}} & {I_{22}^{^k}} \end{array}} \right), $ | (13) |
然后对所有图像块的矩相关矩阵求平均
| $ \begin{array}{l} I = \frac{1}{K}\left( {\begin{array}{*{20}{c}} {\sum\nolimits_{k = 1}^K {I_{00}^{^k}} }&{\sum\nolimits_{k = 1}^K {I_{01}^{^k}} }&{\sum\nolimits_{k = 1}^K {I_{02}^{^k}} }\\ {\sum\nolimits_{k = 1}^K {I_{10}^{^k}} }&{\sum\nolimits_{k = 1}^K {I_{11}^{^k}} }&{\sum\nolimits_{k = 1}^K {I_{12}^{^k}} }\\ {\sum\nolimits_{k = 1}^K {I_{20}^{^k}} }&{\sum\nolimits_{k = 1}^K {I_{21}^{^k}} }&{\sum\nolimits_{k = 1}^K {I_{22}^{^k}} } \end{array}} \right)\\ \;\;\; = \left( {\begin{array}{*{20}{c}} {{I_{00}}}&{{I_{01}}}&{{I_{02}}}\\ {{I_{10}}}&{{I_{11}}}&{{I_{12}}}\\ {{I_{20}}}&{{I_{21}}}&{{I_{22}}} \end{array}} \right). \end{array} $ | (14) |
其中,K为图像中所有图像块的总数,假设图像块中平坦图像块数量为p,非平坦图像块的数量为s。最终,图像的质量分数Q为
| $ Q = \frac{{\frac{1}{9}\sum\limits_{i = 0}^2 {\sum\limits_{j = 0}^2 {{I_{ij}}} } }}{{\left( {0.8p + 0.2s} \right)/K}}. $ | (15) |
在3个图像质量评价数据集LIVE[11]、CSIQ[12]和VCL@FER[13]中进行实验,验证提出方法的实际性能,并与几种具有代表性的图像质量评价方法进行对比,包括PSNR、SSIM[2]、UQI[3]和文献[5]方法。利用Logistic非线性回归方程对主客观评价结果进行非线性回归[5]:
| $ f(x) = \frac{{{\tau _1}-{\tau _2}}}{{1 + {{\rm{e}}^{(x-{\tau _3})/{\tau _4}}}}} + {\tau _2}, $ | (16) |
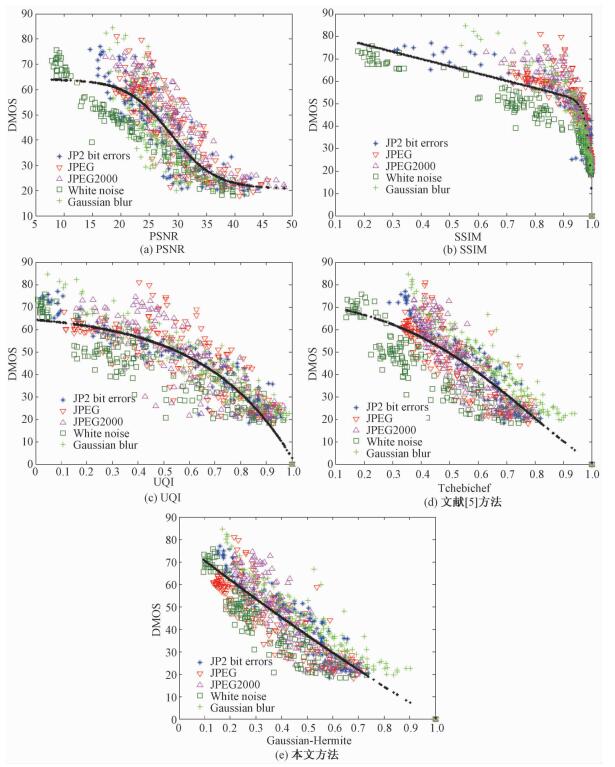
其中,x表示块效应分数,拟合时适当选取τ1、τ2、τ3和τ4的值使得f(x) 与主观质量分数的误差最小。通过Logistic回归方程,可以直观地观察本算法计算的客观质量分数与主观评价结果的一致性。图 3为5种方法的质量评价分数与主观评价分数在LIVE图像库上的拟合曲线。从该图的结果可以看出,本文方法的图像质量评价分数更好地聚集在拟合曲线附近,这说明评价结果与主观评价结果一致性更高,因此该方法性能优于文献[5]的方法。从图 3的结果也可以看出本文方法效果明显优于SSIM、UQI和PSNR方法。
|
Download:
|
|
图 3 在LIVE数据集测试的拟合曲线 Fig. 3 Fitting curves of testing in LIVE dataset |
|
在非线性拟合的基础上,用相关系数 (correlation coefficient, CC) 和均方根误差 (root mean square error, RMSE) 衡量客观分数与主观评价结果的一致性程度;用斯皮尔曼相关系数 (Spearman rank order correlation coefficient, SROCC) 衡量算法的单调性。表 1展示5种方法在LIVE图像数据集中的实验结果,性能最好的结果用黑体突出。由表 1可以看出我们提出的方法效果最好,对于所有失真类型图像综合的CC和SROCC结果均高于其他4种方法,同时RMSE均低于其他4种方法。因此,实验结果表明本文的视频质量评价方法的准确性与单调性很高。
|
|
表 1 LIVE图像数据集中的实验结果比较 Table 1 Comparisons of testing results on LIVE image dataset |
表 2给出本文方法和文献[5]的方法在CSIQ和VCL@FER图像数据集上的实验结果。可以看出本文方法在这两个数据集上的测试性能完全优于文献[5]的方法。
|
|
表 2 CSIQ和VCL@FER图像数据集实验结果比较 Table 2 Comparisons of testing results on CSIQ and VCL@FER image datasets |
连续正交矩在提取图像特征方面优于离散正交矩,基于这一重要特性,对连续正交Gaussian-Hermite矩研究发现,利用该连续正交矩对图像分块进行矩变换,并充分利用矩变换矩阵的矩能量差异,然后结合人类视觉系统的掩盖效应对图像块进行质量评价。通过3个标准图像库上的实验,表明本文所提出的方法的评价结果完全符合主观评价结果,也体现该方法相比现有方法在性能上有明显的提高。
| [1] | 蒋刚毅, 黄大江, 王旭, 等. 图像质量评价方法研究进展[J]. 电子与信息学报, 2010, 32(1):219–226. |
| [2] | Wang Z, Bovik A C, Sheikh H R, et al. Image quality assessment: from error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4):600–612. DOI:10.1109/TIP.2003.819861 |
| [3] | Wang Z, Bovik A C. A universal image quality index[J]. IEEE Signal Processing Letters, 2002, 9(3):81–84. DOI:10.1109/97.995823 |
| [4] | Sheikh H R, Bovik A C. Image information and visual quality[J]. IEEE Transactions on Image Processing, 2006, 15(2):430–444. DOI:10.1109/TIP.2005.859378 |
| [5] | Wee C Y, Paramesran R, Mukundan R, et al. Image quality assessment by discrete orthogonal moments[J]. Pattern Recognition, 2010, 43(12):4055–4068. DOI:10.1016/j.patcog.2010.05.026 |
| [6] | Mukundan R, Ong S H, Lee P A. Image analysis by Tchebichef moments[J]. IEEE Transactions on Image Processing, 2001, 10(9):1357–1364. DOI:10.1109/83.941859 |
| [7] | Yap P T, Paramesran R, Ong S H. Image analysis by Krawtchouk moments[J]. IEEE Transactions on Image Processing, 2003, 12(11):1367–1377. DOI:10.1109/TIP.2003.818019 |
| [8] | Yang B, Dai M. Image analysis by Gaussian-Hermite moments[J]. Signal Processing, 2011, 91(10):2290–2303. DOI:10.1016/j.sigpro.2011.04.012 |
| [9] | 吴金建. 基于人类视觉系统的图像信息感知和图像质量评价[D]. 西安: 西安电子科技大学, 2014. |
| [10] | Li L, Zhu H, Yang G, et al. Referenceless measure of blocking artifacts by tchebichef kernel analysis[J]. IEEE Signal Processing Letters, 2014, 21(1):122–125. DOI:10.1109/LSP.2013.2294333 |
| [11] | Sheikh H R, Wang Z, Cormack L, et al. LIVE image quality assessment database release 2[EB/OL].(2006)[2017-01-15].http://live.ece.utexas.edu/research/quality. |
| [12] | Larson E C, Chandler D M. Categorical subjective image quality CSIQ database[EB/OL]. (2009-04-24)[2017-01-15]. http://vision.okstate.edu/csiq/. |
| [13] | Zaric A, Tatalovic N, Brajkovic N, et al. Vcl@fer image quality assessment database[J]. Automatika Journal for Control Measurement Electronics Compu, 2012, 53(4):105–110. |
 2017, Vol. 34
2017, Vol. 34 


