Over the past three decades, unconventional superconductivity with gap symmetry other than s-wave has been found in several classes of materials, including the heavy-Fermion superconductors with or without the spatial inversion symmetry, the high-Tc superconductors, and the organic superconductors[1-2]. The study of exotic properties of unconventional superconductors has become a central issue in the field of condensed matter physics. Most of unconventional superconductors have nodes (zeros) in the gap functions along certain directions in the momentum space. Since the nodal structure is intimately related to the pairing interaction, its identification is of fundamental importance. The anisotropic nodal structure in unconventional superconductors has mainly been investigated by probing the thermally excited quasiparticles. Experimentally, the temperature dependence of several thermodynamic quantities and transport coefficients such as electronic specific heat Ce(T), nuclear magnetic resonance relaxation rate T1-1(T), London penetration depth λ(T), and thermal conductivity κ(T) have been extensively used so far to explore the nodal topology of unconventional superconductors.
For a superconductor with the order parameter belonging to a one-dimensional representation of a given crystal symmetry, the nodal topology is restricted to either line nodes or point nodes. The existence of Bogolubov quasiparticle excitations in the neighborhood of these nodes gives rise to a non-BCS behaviour in the temperature dependence of thermodynamic quantities and transport coefficients, particularly at low temperatures where the contributions from the nodes are dominant. In the clean limit, the thermodynamic quantities and transport coefficients exhibit a power-law ~Tn temperature dependence as T→0, other than an exponential temperature dependence exp (-Δ0/T) as in the case of the fully gapped s-wave superconductor. According to the generalized BCS theory, the power-laws in temperature depend on only the dimension of the structures of gap nodes (i.e., points or lines) and the rate at which the gap vanishes in the neighborhood of the nodes. In the case of electronic specific heat Ce(T), one has n=3 for point nodes with linearly varying gap amplitude around the nodal point, and n=2 for line nodes as well as point nodes where the gap is quadratic in distance from the nodal point in the momentum space[3-4].
However, the hint in the nodal structure might be hidden by some extrinsic origins of low-lying states within energy gap. Impurities are at the forefront of the extrinsic origin. Scattering by a sufficiently small amount of impurities in unconventional superconductors may cause decrease in the critical temperature and bring in changes in the nodal structure leading to the power-law dependence ineffective. This issue is discussed extensively within and beyond the Born approximation[5-8]. Another extrinsic origin leading to similar effects might be an applied weak Zeeman magnetic field (ZF) which breaks the time-reversal symmetry. Recently the role of a weak ZF in the noncentrosymmetric superconductors[2], where the Cooper pair state is a mixture of spin-singlet and spin-triplet states, has been discussed by several authors[9-11]. The stability of the suggested accidental line nodes[12-13] and the possible types of nodal structures induced by ZF have been the focuses of discussion[9, 14]. In this work, we investigate how the nodal structure in pure nodal spin-singlet and spin-triplet states as well as the power-law temperature dependence for electronic specific heat are affected by an applied weak ZF.
1 FormulationLet us consider a superconductor modeled by the Bogoliubov-de Gennes Hamiltonian
| $ H = {H_0} + {H_{\operatorname{int} }}. $ | (1) |
The first term H0 is for a noninteracting conduction electron system subjected to a ZF,
| $ {H_0} = \sum\limits_k {\sum\limits_{\alpha ,\beta } {\left( {{ϵ_k}{\mathit{\boldsymbol{\sigma }}_0} + \mathit{\boldsymbol{h}} \cdot \mathit{\boldsymbol{\sigma }}} \right){}_{\alpha \beta }c_{\mathit{\boldsymbol{k}}\alpha }^\dagger {c_{\mathit{\boldsymbol{k}}\beta }}} } , $ | (2) |
where ckα†(ckα) creates (annihilates) an electron with wave vector k=k(sinθkcosϕk, sinθksinϕk, cosθk) and spin α, σ=(σx, σy, σz) denotes the Pauli matrices, σ0 is the 2×2 unit matrix, ϵk is the parabolic bare band dispersion measured relative to the chemical potential μ and restricted to |ϵk| < ωc with ωc being the usual cutoff energy. The ZF is specified by h=h(sinθhcosϕh, sinθhsinϕh, cosθh).
The second term in (1) describes the pairing interaction
| $ \begin{array}{*{20}{c}} {{H_{{\mathop{\rm int}} }} = \frac{1}{2}\sum\limits_\mathit{\boldsymbol{k}} {\sum\limits_{\alpha ,\beta } {\left[ {{\Delta _{\mathit{\boldsymbol{k,}}\alpha \beta }}c_{\mathit{\boldsymbol{k}}\alpha }^\dagger c_{ - \mathit{\boldsymbol{k}}\beta }^\dagger + } \right.} } }\\ {\left. {c_{\mathit{\boldsymbol{k}},\alpha \beta }^\dagger {c_{ - \mathit{\boldsymbol{k}}\alpha }}{c_{\mathit{\boldsymbol{k}}\beta }} + {\Delta _{\mathit{\boldsymbol{k,}}\alpha \beta }}F_{\mathit{\boldsymbol{k}},\beta \alpha }^\dagger } \right],} \end{array} $ | (3) |
with the anomalous averages Fk, αβ=〈ckαc-kβ〉, and the gap function defined by
| $ {\Delta _{\mathit{\boldsymbol{k,}}\alpha \beta }} = - \sum\limits_{\mathit{\boldsymbol{k'}}} {\sum\limits_{\lambda ,\mu } {{V_{\beta \alpha ,\lambda \mu }}\left( {\mathit{\boldsymbol{k}},\mathit{\boldsymbol{k'}}} \right){F_{\mathit{\boldsymbol{k'}},\lambda \mu }}} } , $ | (4) |
where Vαβ, λμ(k, k′) denotes the pairing potential. The Pauli principle requires that Δk, αβ=-Δ-k, βα.
By using the Nambu vector operator, Ψk=(ck↑, ck↓, c-k↑†, c-k↓†)T, where (…)T stands for the transposing operation, we can rewrite the Hamiltonian in a more compact form
| $ H = \frac{1}{2}\sum\limits_\mathit{\boldsymbol{k}} {\mathit{\boldsymbol{\psi }}_\mathit{\boldsymbol{k}}^\dagger \mathop {{\mathit{\boldsymbol{H}}_\mathit{\boldsymbol{k}}}}\limits^ \vee {\mathit{\boldsymbol{\psi }}_\mathit{\boldsymbol{k}}}} + \sum\limits_\mathit{\boldsymbol{k}} {{ϵ_k}} + \frac{1}{2}\sum\limits_\mathit{\boldsymbol{k}} {\sum\limits_{\alpha ,\beta } {{\Delta _{\mathit{\boldsymbol{k,}}\alpha \beta }}F_{\mathit{\boldsymbol{k}},\beta \alpha }^\dagger } } , $ | (5) |
where
| $ \mathop {{\mathit{\boldsymbol{H}}_\mathit{\boldsymbol{k}}}}\limits^ \vee = \left( {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat M}}}_\mathit{\boldsymbol{k}}}}&{{{\mathit{\boldsymbol{ \boldsymbol{\hat \varDelta} }}}_\mathit{\boldsymbol{k}}}}\\ {\mathit{\boldsymbol{ \boldsymbol{\hat \varDelta} }}_\mathit{\boldsymbol{k}}^\dagger }&{ - \mathit{\boldsymbol{\hat M}}_{ - \mathit{\boldsymbol{k}}}^ * } \end{array}} \right), $ | (6) |
with
| $ {{\mathit{\boldsymbol{\hat M}}}_\mathit{\boldsymbol{k}}} = {ϵ_k}{\mathit{\boldsymbol{\sigma }}_0} + \mathit{\boldsymbol{h}} \cdot \mathit{\boldsymbol{\sigma }}. $ | (7) |
The gap matrix
| $ {{\mathit{\boldsymbol{ \boldsymbol{\hat \varDelta} }}}_\mathit{\boldsymbol{k}}} = \left\{ \begin{array}{l} {\Delta _s}{\psi _k}\left( {{\rm{i}}{\sigma _y}} \right)\;\;\;\;\;\;\;{\rm{for}}\;{\rm{spin - singlet,}}\\ {\Delta _t}{\mathit{\boldsymbol{d}}_k} \cdot \mathit{\boldsymbol{\sigma }}\left( {{\rm{i}}{\sigma _y}} \right)\;\;\;\;{\rm{for}}\;{\rm{spin - triplet,}} \end{array} \right. $ | (8) |
where the amplitudes Δs and Δt are chosen to be real and positive.
The pairing potentials in (4) are taken to be
| $ {V_{\alpha \beta ,\lambda \mu }}\left( {\mathit{\boldsymbol{k}},\mathit{\boldsymbol{k'}}} \right) = - \frac{{{V_s}}}{2}{\left( {{\psi _\mathit{\boldsymbol{k}}}{\rm{i}}{\sigma _y}} \right)_{\alpha \beta }}\left( {{\psi _{\mathit{\boldsymbol{k'}}}}{\rm{i}}{\sigma _y}} \right)_{\lambda \mu }^\dagger $ | (9) |
for spin-singlet states, and
| $ {V_{\alpha \beta ,\lambda \mu }}\left( {\mathit{\boldsymbol{k}},\mathit{\boldsymbol{k'}}} \right) = - \frac{{{V_t}}}{2}{\left( {{\mathit{\boldsymbol{d}}_\mathit{\boldsymbol{k}}} \cdot \mathit{\boldsymbol{\sigma }}{\rm{i}}{\sigma _y}} \right)_{\alpha \beta }}\left( {{\mathit{\boldsymbol{d}}_{\mathit{\boldsymbol{k'}}}} \cdot \mathit{\boldsymbol{\sigma }}{\rm{i}}{\sigma _y}} \right)_{\lambda \mu }^\dagger $ | (10) |
for spin-triplet states, where Vs, Vt>0.
The excitation spectrum of Bogoliubov-de Gennes quasiparticle E(k) can be obtained readily by diagonalizing the matrix Ȟk in (6). For the ZF oriented in the direction (θh, ϕh), one can generally find four solutions, namely, E±(e)(k) and E±(h)(k), with E±(h)(k)=-E±(e)(-k). The electronic specific heat Ce can be expressed as
| $ {C_e} = \sum\limits_\mathit{\boldsymbol{k}} {\sum\limits_{\gamma = \pm } {E_\gamma ^{\left( e \right)}\left( \mathit{\boldsymbol{k}} \right)} } \frac{{\partial {f_{\mathit{\boldsymbol{k}}\gamma }}}}{{\partial T}}, $ | (11) |
where
| $ {f_{\mathit{\boldsymbol{k}}\gamma }} = f\left( {E_\gamma ^{\left( e \right)}\left( \mathit{\boldsymbol{k}} \right)} \right) = \frac{1}{{\exp \left( {E_\gamma ^{\left( e \right)}\left( \mathit{\boldsymbol{k}} \right)/T} \right) + 1}}. $ | (12) |
Temperature dependence of the gap amplitude Δs or Δt is determined by the gap equation
| $ {\Delta _\alpha } = {V_\alpha }\sum\limits_{\mathit{\boldsymbol{k}}\gamma } {\frac{{\tanh \left( {E_{\alpha \gamma }^{\left( e \right)}\left( \mathit{\boldsymbol{k}} \right)/2T} \right)}}{4}\frac{{\partial E_{\alpha \gamma }^{\left( e \right)}\left( \mathit{\boldsymbol{k}} \right)}}{{\partial {\Delta _\alpha }}}} , $ | (13) |
with α=s or t.
2 Results and discussionThe nodal structure of a superconducting state is determined by zeros of quasiparticle excitation spectra E±(e)(k) in momentum space. We first consider the spin-singlet case. The quasiparticle excitation spectra of spin-singlet state take a simple form in the presence of ZF,
| $ E_{s \pm }^{\left( e \right)}\left( \mathit{\boldsymbol{k}} \right) = \sqrt {ϵ_k^2 + \Delta _s^2 + {{\left| {{\psi _\mathit{\boldsymbol{k}}}} \right|}^2}} \pm h. $ | (14) |
As can be seen, Es±(e)(k) are independent of the orientation of the ZF, an important feature specific to spin-singlet states. It is evident that the upper branch Es+(e)(k) has no node, while the lower branch Es-(e)(k) may show nodes when
| $ {\Delta _s}\left| {{\psi _\mathit{\boldsymbol{k}}}} \right| \le h. $ | (15) |
For h=0 this condition becomes
| $ \left| {{\psi _\mathit{\boldsymbol{k}}}} \right| = 0. $ | (16) |
Equations (15) and (16) imply that, for nodal spin-singlet state, new nodes can be induced in the vicinity of the original nodal points or lines by an arbitrarily orientated weak ZF. For example, we consider two typical d-wave states
| $ {\psi _\mathit{\boldsymbol{k}}} = \left\{ \begin{array}{l} 2\hat k_z^2 - \hat k_x^2 - \hat k_y^2\;\;\;\;\;\;\;\;\;\;\left( {{d_{2{z^2} - {x^2} - {y^2}}} - {\rm{wave}}} \right),\\ \left( {\hat k_x^2 - \hat k_x^2} \right) + {\rm{i}}{{\hat k}_x}{{\hat k}_y}\;\;\;\;\;\;\left( {{d_{{x^2} - {y^2}}} + {\rm{i}}{d_{xy}} - {\rm{wave}}} \right). \end{array} \right. $ | (17) |
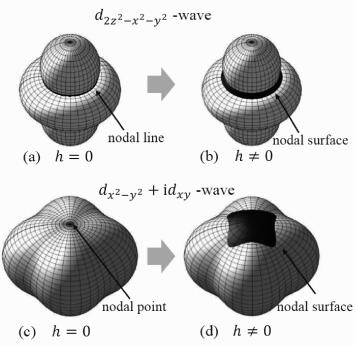
The d2z2-x2-y2-wave state possesses two isolated line nodes locating at θk=arccos
|
Download:
|
|
(a) and (b) for d2z2-x2-y2-wave; (c) and (d) for dx2-y2+idxy-wave. The black areas denote the induced nodal surfaces. Fig. 1 Schematic illustration of the evolution of the nodal structure under the influence of ZF |
|
The change in nodal topology will be reflected on the temperature dependence of electronic specific heat at low temperatures. In the absence of ZF, the temperature dependence of specific heat of our two d-wave states follows the standard power-law dependence Ce(T)~T2. However, an arbitrarily weak ZF (irrespective of its orientation) can result in change in the exponent, and we have Ce(T)~T for h≠0. In Fig. 2 we present the normalized electronic specific heat Ce(T)/Cn(T) as a function of T/Tc for d2z2-x2-y2-wave and dx2-y2+idxy-wave at several values of h, where Cn(T) denotes the specific heat in normal state, and Tc is the critical temperature calculated at h=0.

|
Download:
|
|
Fig. 2 Temperature dependence of electronic specific heat at low temperatures at several values of h |
|
Now let us turn to the spin-triplet case. In this work we will confine ourselves to the so-called unitary phase for which dk×dk*=0 for all k. In the presence of ZF, the quasiparticle excitation spectra can be expressed as
| $ E_{t \pm }^{\left( e \right)}\left( \mathit{\boldsymbol{k}} \right) = \sqrt {ϵ_k^2 + {h^2} + \Delta _t^2{{\left| {{\mathit{\boldsymbol{d}}_\mathit{\boldsymbol{k}}}} \right|}^2} \pm 2{S_k}} . $ | (18) |
| $ {S_k} = \sqrt {\left( {ϵ_k^2 + \Delta _t^2{{\left| {{\mathit{\boldsymbol{d}}_\mathit{\boldsymbol{k}}}} \right|}^2}} \right){h^2} - \Delta _t^2{{\left| {{\mathit{\boldsymbol{d}}_\mathit{\boldsymbol{k}}} \times \mathit{\boldsymbol{h}}} \right|}^2}} . $ | (19) |
For h=0, Et±(e)(k) may have nodes at momentum k where |dk|=0 on the Fermi surface. However, Et+(e)(k) is positive definite in the h≠0 case. Thereby we only need to discuss the zeros of the lower branch Et-(e)(k). Now Et-(e)(k) depends on both magnitude and orientation of ZF. Since the Hermitian property of Ȟk ensures that the eigenvalue Et-(e)(k) is real, we get the inequality
| $ ϵ_k^2 + {h^2} + \Delta _t^2{\left| {{\mathit{\boldsymbol{d}}_\mathit{\boldsymbol{k}}}} \right|^2} - 2{S_k} \ge 0, $ | (20) |
which can be rewritten as
| $ {\left( {ϵ_k^2 - {h^2} + \Delta _t^2{{\left| {{\mathit{\boldsymbol{d}}_\mathit{\boldsymbol{k}}}} \right|}^2}} \right)^2} + 4\Delta _t^2{\left| {{\mathit{\boldsymbol{d}}_\mathit{\boldsymbol{k}}} \times \mathit{\boldsymbol{h}}} \right|^2} \ge 0. $ | (21) |
Evidently, Et-(e)(k)=0 only if the following conditions are satisfied simultaneously:
| $ ϵ_k^2 - {h^2} + \Delta _t^2{\left| {{\mathit{\boldsymbol{d}}_\mathit{\boldsymbol{k}}}} \right|^2} = 0,\;\;\;\left| {{\mathit{\boldsymbol{d}}_\mathit{\boldsymbol{k}}} \times \mathit{\boldsymbol{h}}} \right| = 0. $ | (22) |
For h=0 these conditions are reduced to
| $ \left| {{\mathit{\boldsymbol{d}}_\mathit{\boldsymbol{k}}}} \right| = 0. $ | (23) |
Eq. (22) indicates that, in the presence of ZF, the energy gap in the quasiparticle excitation spectrum closes in the (θk, ϕk) direction on the Fermi surface, when
| $ {\Delta _t}\left| {{\mathit{\boldsymbol{d}}_\mathit{\boldsymbol{k}}}} \right| \le \mathit{\boldsymbol{h}} $ | (24) |
for dk×h=0, and
| $ \left| {{\mathit{\boldsymbol{d}}_\mathit{\boldsymbol{k}}}} \right| = 0 $ | (25) |
for dk×h≠0. In the presence of ZF it is convenient to introduce an opposite spin pairing (OSP) state (for which dk×h=0 for all k) and an equal spin pairing (ESP) state (for which dk·h=0 for all k)[14]. Then the spin-triplet states can be separated into three classes: those that contain only OPS states, those that contain only ESP states, and those that contain both OSP and ESP states. The spin-singlet states can be classified as the OPS states. We note that the condition Eq. (24) for dk×h=0 is similar to that of spin-singlet case [Eq. (15)]. This result is reasonable since in such a configuration both spin-singlet and spin-triplet states belong to the OSP states. On the other hand, Eq. (25) states that no additional nodes can be created by ZF at momentum k on the Fermi surface provided that h and dk are non-collinear, in strong contrast with the spin-singlet case.
Now let us consider two special types of nodal p-wave states for which the d-vectors are independent of the momentum k. Here for illustrative purposes we choose the A-phase and Polar-phase in superfluid 3He. The d-vectors[4] can be written as
| $ {\mathit{\boldsymbol{d}}_\mathit{\boldsymbol{k}}} = \left\{ \begin{array}{l} \mathit{\boldsymbol{x}}\left( {{{\hat k}_x} + {\rm{i}}{{\hat k}_y}} \right),\;\;\;\;{\rm{A - phase,}}\\ z{{\hat k}_z},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{Polar - phase}}{\rm{.}} \end{array} \right. $ | (26) |
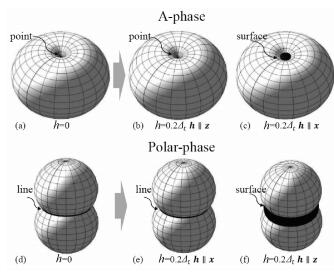
The effects of non-magnetic impurity scattering on the thermodynamic quantities in these states were extensively discussed previously[5-8]. At h=0, the A-phase shows the same nodal structure as that of the dx2-y2+idxy-wave state but with the point nodes of first-order, while the Polar-phase possesses line node which is located on the equatorial circle on the Fermi surface. As discussed above, no change in nodal topology would take place for our two phases as long as dk×h≠0. In the h‖dk case, however, they are in the OSP states and the point and line nodes are replaced by nodal surfaces (see Fig. 3), similar to the spin-singlet case discussed above.
|
Download:
|
|
(a)-(c) are for A-phase, and (d)-(f) for Polar-phase Fig. 3 A surface node created by ZF only when the two vectors h and dk are collinear |
|
We display in Fig. 4 the temperature dependence of electronic specific heat for the A-phase and Polar-phase. In the absence of ZF, the temperature dependence of electronic specific heat for our two phases obey the standard power-law dependence, and we have Ce(T)~T3 for A-phase and Ce(T)~T2 for Polar-phase. As can be seen, the exponents are unchanged as long as dk×h≠0. For the h‖dk case, however, we obtain n=1 for both phases, as in the case of our spin-singlet states. Note that, when h‖z (h‖x) the A-phase (Polar-phase) is in the ESP state and the Ce(T) varieswith temperature as if h=0.

|
Download:
|
|
Fig. 4 Calculated temperature dependence of specific heat for A-phase (a) and Polar-phase with different h (b) |
|
We proceed to discuss the opposite situation for which the direction of d-vector is a function of k. Here we consider a set of nodal p-wave states[15] given by
| $ {\mathit{\boldsymbol{d}}_\mathit{\boldsymbol{k}}} = \left\{ \begin{array}{l} \mathit{\boldsymbol{x}}{{\hat k}_x} \pm \mathit{\boldsymbol{y}}{{\hat k}_y},\\ \mathit{\boldsymbol{x}}{{\hat k}_y} \pm \mathit{\boldsymbol{y}}{{\hat k}_x}. \end{array} \right. $ | (27) |
Note that the d-vectors are confined within the x-y plane. In the absence of ZF, these states exhibit two point nodes of first-order locating at the poles as in the case of A-phase. This nodal structure is unchanged for a ZF not lying in the x-y plane since dk×h≠0 in this configuration. When ZF is applied along the (θh=π/2, ϕh) direction, however, the condition given in (24) yields two line nodes across the south and north poles on the Fermi surface, with the size of line node limited by

|
Download:
|
|
Fig. 5 Nodal lines for |
|
| $ \left\{ \begin{array}{l} \sin \left( {{\phi _k} \mp {\phi _h}} \right) = 0\;\;{\rm{for}}\;\;{\mathit{\boldsymbol{d}}_\mathit{\boldsymbol{k}}} = \mathit{\boldsymbol{x}}{{\hat k}_x} \pm \mathit{\boldsymbol{y}}{{\hat k}_y},\\ \cos \left( {{\phi _k} \mp {\phi _h}} \right) = 0\;\;{\rm{for}}\;\;{\mathit{\boldsymbol{d}}_\mathit{\boldsymbol{k}}} = \mathit{\boldsymbol{x}}{{\hat k}_y} \pm \mathit{\boldsymbol{y}}{{\hat k}_x}. \end{array} \right. $ | (28) |
The location of line node depends on the angle ϕh.
Plotted in Fig. 6 is the temperature dependence of electronic specific heat for our states cited above. At h=0, we have Ce(T)~T3 as expected. For h‖z, our states are in the ESP states. Therefore the resultant curve is coincident with that for the h=0 case. This T3 dependence of Ce(T) is maintained as long as θh≠π/2. When h‖x, the exponent is modified to be n=2 due to the appearance of the induced line nodes mentioned above. It is noted that no quasiparticle excitation exists at T=0 now because of the lack of nodal surface. Finally we discuss in passing the B-phase of superfluid 3He where the d-vector is given by

|
Download:
|
|
Fig. 6 Calculated temperature dependence of specific heat for |
|
In summary, we have systematically investigated the effects of a weak ZF on the nodal structures of nodal spin-singlet and nodal unitary spin-triplet superconductors. Detailed analysis of the quasiparticle excitation spectrum indicates that the nodal structure can be changed profoundly under the influence of ZF. This result is corroborated by numerical computations of the low-temperature electronic specific heat Ce(T). We find especially that, for the spin-singlet superconductors or spin-triplet superconductors in the OSP states, a weak ZF may convert the original isolated point or line nodes into surface nodes, which is responsible for the Ce(T)~T dependence at low temperatures. In addition, the low-temperature electronic specific heat for spin-triple states is found to be sensitive to the relative orientation between h and dk in a rather peculiar way. We hope that our results would be helpful for identifying the order-parameter symmetry of nodal superconductors.
| [1] | Bennemann K H, Ketterson J B. Superconductivity[M]. Berlin: Springer, 2008. |
| [2] | Kimura N, Bonalde I. Non-centrosymmetric heavy-fermion superconductors[C]//Bauer E, Sigrist M. Non-Centrosymmetric Superconductors. Berlin: Springer, 2012: 35-80. |
| [3] | Volovik G E, Gor'kov L P. Superconducting classes in heavy fermions systems[J]. Zh Eksp Teor Fiz, 1985, 88(4):1412–1429. |
| [4] | Mineev V P, Samokhin K V. Introduction to unconventional superconductivity[M]. London: Gordon and Breach, 1999. |
| [5] | Gor'kov L P, Kalugin P A. Defects and an unusual superconductivity[J]. Pis'ma Zh Eksp Teor Fiz, 1985, 41(5):208–210. |
| [6] | Ueda K, Rice T M. Heavy electron superconductors-some consequences of the p-wave[C]//Kasuya T, Saso T. Theory of Heavy Fermions and Valence Fluctuations. Berlin: Springer, 1985: 267-276. |
| [7] | Pethick C J, Pines D. Transport processes in heavy-fermion superconductors[J]. Phys Rev Lett, 1986, 57(1):118–121. DOI:10.1103/PhysRevLett.57.118 |
| [8] | Hirschfeld P J, Wölfle P, Einzel D. Consequences of resonant impurity scattering in anisotropic superconductors: thermal and spin relaxation properties[J]. Phys Rev B, 1988, 37(1):83–97. DOI:10.1103/PhysRevB.37.83 |
| [9] | Eremin I, Annett J F. Magnetic field dependence of the superconducting gap node topology in noncentrosymmetric CePt3Si[J]. Phys Rev B, 2006, 74(18):184524–1. DOI:10.1103/PhysRevB.74.184524 |
| [10] | Fujimoto S. Theory of parity-violated Cooper pairs in weakly noncentrosymmetric superconductors[J]. Phys Rev B, 2007, 76(18):184504–1. DOI:10.1103/PhysRevB.76.184504 |
| [11] | Chen C, Jin B. Zeeman field-induced nodal structures in rashba-type noncentrosymmetric superconductors[J]. J Low Temp Phys, 2016, 182(3/4):124–138. |
| [12] | Hayashi N, Wakabayashi K, Frigeri P A, et al. Temperature dependence of the superfluid density in a noncentrosymmetric superconductor[J]. Phys Rev B, 2006, 73(2):024504–1. DOI:10.1103/PhysRevB.73.024504 |
| [13] | Hayashi N, Wakabayashi K, Frigeri P A, et al. Nuclear magnetic relaxation rate in a noncentrosymmetric superconductor[J]. Phys Rev B, 2006, 73(9):092508–1. DOI:10.1103/PhysRevB.73.092508 |
| [14] | Powell B J, Annett J F, Györffy B L. The gap equations for spin singlet and triplet ferromagnetic superconductors[J]. J Phys A Math Gen, 2003, 36(35):9289–9302. DOI:10.1088/0305-4470/36/35/314 |
| [15] | Sigrist M, Ueda K. Phenomenological theory of unconventional superconductivity[J]. Rev Mod Phys, 1991, 63(2):239–311. DOI:10.1103/RevModPhys.63.239 |
 2017, Vol. 34
2017, Vol. 34 


