Any actual system is always moving or working under a variety of occasional and ongoing disturbances. When the system is under disturbance, whether the system can safely keep the motion track or working condition, that is, the stability of the system is the most important consideration. The stability of a system includes the stability of the equilibrium state and the stability of any motion. The stability of a given motion can be transformed into the stability of the equilibrium point. The stability of equilibrium point is defined as Lyapunov stability, uniform stability, asymptotic stability, uniform asymptotic stability, exponential asymptotic stability, or global asymptotic stability. The best general reference here is Ref.[1]. It is very important for a system to have good stability properties. However, some systems are not stable. When a system is not stable, our idea in this work is to add a forced term to the system, which makes the system have good stability properties, such as global asymptotic stability or asymptotic stability. We can adjust the form of the forced term to make it physically meaningful and be easily added to the actual system. This idea comes from the study of fuzzy logic control systems. Fuzzy logic controllers was proposed long ago and applied successfully in many applications[2-7]. A comprehensive work on the proof of stability of fuzzy logic control systems represents one of the challenges in fuzzy control[8-11]. This work is based on the research on the fuzzy logic control systems. It is innovative to add a physical forced term to the system for the asymptotic stability. To add the suitable forced terms, we propose two new methods, which are dependent upon the analyses of the stability. For this purpose, we introduce various methods for studying the stability of systems.
1 Systems with forced termThe structure of a system with forced term is presented in this section. Let X be the universe of discourse and consider a system with x=0 an equilibrium point of the following form:
| $ \mathit{\boldsymbol{\dot x = }}f\left( \mathit{\boldsymbol{x}} \right),\mathit{\boldsymbol{x}} \in {R^n},\mathit{\boldsymbol{f}}\left( \mathit{\boldsymbol{x}} \right) = {\left( {{f_1}\left( \mathit{\boldsymbol{x}} \right),{f_2}\left( \mathit{\boldsymbol{x}} \right), \cdots ,{f_n}\left( \mathit{\boldsymbol{x}} \right)} \right)^{\rm{T}}}. $ | (1) |
If system (1) is not stable, we want to add the forced term to the system (the external effect in the actual problem) to make the system asymptotically stable and have good properties. The problem we need to study is the form of the forced term. In view of the actual physical problems, for the convenience of adding an external effect in the actual operation, we assume that the form of adding items as
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{D}}\left( \mathit{\boldsymbol{x}} \right) = \mathit{\boldsymbol{b}}\left( \mathit{\boldsymbol{x}} \right)u\left( \mathit{\boldsymbol{x}} \right),}\\ {\mathit{\boldsymbol{b}}\left( \mathit{\boldsymbol{x}} \right) = {{\left( {{b_1}\left( \mathit{\boldsymbol{x}} \right),{b_2}\left( \mathit{\boldsymbol{x}} \right), \cdots .,{b_n}\left( \mathit{\boldsymbol{x}} \right)} \right)}^{\rm{T}}},} \end{array} $ |
where u(x) is a scalar function.
Then, we consider the stability of a system with forced term of the form
| $ \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{f}}\left( \mathit{\boldsymbol{x}} \right) + \mathit{\boldsymbol{D}}\left( \mathit{\boldsymbol{x}} \right) = \mathit{\boldsymbol{f}}\left( \mathit{\boldsymbol{x}} \right) + \mathit{\boldsymbol{b}}\left( \mathit{\boldsymbol{x}} \right)u\left( \mathit{\boldsymbol{x}} \right). $ | (2) |
In the study of an actual physical problem, for the convenience of adding external effects, the form of b(x) in system (2) is given in advance. So the next work is to look for u(x) which makes system (2) asymptotically stable while b(x) is given in a different form.
2 Stability analysis of general systems with forced termThe stability analysis presented in this section is based on LaSalle's invariance principle cited and analyzed in Refs.[12-15]. This section is concentrated on the formulation and proof of Theorem 2.1 that ensures sufficient conditions for the stability of general autonomous system.
The Lyapunov function candidate V:Rn→R, V(x)=xTPx is considered. It is positive and unbounded, and P∈Rn×n is a positive definite matrix. Then, because P is a positive define matrix, P=QTQ, where Q is an upper triangular matrix in which the diagonal elements are positive. Next we introduce a kind of linear transformation y=Qx to system (2), and then it becomes the system,
| $ \mathit{\boldsymbol{\dot y = g}}\left( \mathit{\boldsymbol{y}} \right) + \mathit{\boldsymbol{c}}\left( \mathit{\boldsymbol{y}} \right)v\left( \mathit{\boldsymbol{y}} \right), $ | (3) |
where g(y)=Qf(Q-1y), c(y)=Qb(Q-1y), and v(y)=u(Q-1y).
So we only need to obtain v(y) in this system, and u(x) can be obtained by the linear transformation y=Qx. Now we know V(x)=xTPx=yTy. Consider the derivatives of V with respect to time expressed in terms of (4):
| $ \begin{array}{l} \Omega = \dot V\left( \mathit{\boldsymbol{x}} \right)\\ \;\;\;\; = 2\left( {{{\dot y}_1}{y_1} + \cdots + {{\dot y}_n}{y_n}} \right)\\ \;\;\;\; = 2\left( {{\mathit{\boldsymbol{y}}^{\rm{T}}}\mathit{\boldsymbol{g}}\left( \mathit{\boldsymbol{y}} \right) + {\mathit{\boldsymbol{y}}^{\rm{T}}}\mathit{\boldsymbol{c}}\left( \mathit{\boldsymbol{y}} \right)v\left( \mathit{\boldsymbol{y}} \right)} \right)\\ \;\;\;\; = G\left( \mathit{\boldsymbol{y}} \right) + C\left( \mathit{\boldsymbol{y}} \right)v\left( \mathit{\boldsymbol{y}} \right), \end{array} $ | (4) |
where G(y)=2yTg(y), C(y)=2yTc(y).
The following sets are defined to be used in the stability analysis:
| $ \begin{array}{l} \;\;\;\;\;\;\;{C^0} = \left\{ {\mathit{\boldsymbol{y}} \in Y\left| {C\left( \mathit{\boldsymbol{y}} \right) = 0} \right.} \right\},{C^ + } = \left\{ {\mathit{\boldsymbol{y}} \in Y} |\right.\\ \left. {C\left( \mathit{\boldsymbol{y}} \right) > 0} \right\},{C^ - } = \left\{ {\mathit{\boldsymbol{y}} \in Y\left| {C\left( \mathit{\boldsymbol{y}} \right) < 0} \right.} \right\}, \end{array} $ |
where Y is the universe transformed from X by y=Qx.
Theorem 2.1 Suppose that y=0 is an equilibrium point of system (3), in other words, x=0 is an equilibrium point of system (2). If the following conditions hold:
1) G(y)≤0, ∀y∈C0;
2)
3) Set {y∈Y|Ω=0} contains no state trajectories except the trivial one, y(t)=0, t≥0.
Then system (2) is globally asymptotically stable in the sense of Lyapunov at the origin.
Proof From the definition of V it results that V(0)=0, V(x)>0, ∀x≠0 and V(x)=xTPx→∞ as ‖x‖→∞. Further it will be proved that
Case 1: If y0∈C0, it results that
| $ \dot V\left( {{\mathit{\boldsymbol{x}}_0}} \right) = G\left( {{\mathit{\boldsymbol{y}}_0}} \right) + C\left( {{\mathit{\boldsymbol{y}}_0}} \right)v\left( {{\mathit{\boldsymbol{y}}_0}} \right) = G\left( {{\mathit{\boldsymbol{y}}_0}} \right) \le 0. $ |
Case 2: If y0∈C+, from the condition 2) of Theorem 2.1 it results that
| $ \begin{array}{l} v\left( {{\mathit{\boldsymbol{y}}_0}} \right) \le - \frac{{G\left( {{\mathit{\boldsymbol{y}}_0}} \right)}}{{C\left( {{\mathit{\boldsymbol{y}}_0}} \right)}}\\ \Rightarrow \dot V\left( {{\mathit{\boldsymbol{x}}_0}} \right) = G\left( {{\mathit{\boldsymbol{y}}_0}} \right) + C\left( {{\mathit{\boldsymbol{y}}_0}} \right)v\left( {{\mathit{\boldsymbol{y}}_0}} \right) \le G\left( {{\mathit{\boldsymbol{y}}_0}} \right) + \\ C\left( {{\mathit{\boldsymbol{y}}_0}} \right)\left( { - \frac{{G\left( {{\mathit{\boldsymbol{y}}_0}} \right)}}{{C\left( {{\mathit{\boldsymbol{y}}_0}} \right)}}} \right) = 0. \end{array} $ |
Therefore,
| $ v\left( {{\mathit{\boldsymbol{y}}_0}} \right) \le - \frac{{G\left( {{\mathit{\boldsymbol{y}}_0}} \right)}}{{C\left( {{\mathit{\boldsymbol{y}}_0}} \right)}} \Rightarrow \dot V\left( {{\mathit{\boldsymbol{x}}_0}} \right) \le 0. $ |
Case 3: If y0∈C-, from the condition 2) of Theorem 2.1 it results that
| $ \begin{array}{l} v\left( {{\mathit{\boldsymbol{y}}_0}} \right) \ge - \frac{{G\left( {{\mathit{\boldsymbol{y}}_0}} \right)}}{{C\left( {{\mathit{\boldsymbol{y}}_0}} \right)}}\\ \Rightarrow \dot V\left( {{\mathit{\boldsymbol{x}}_0}} \right) = G\left( {{\mathit{\boldsymbol{y}}_0}} \right) + C\left( {{\mathit{\boldsymbol{y}}_0}} \right)v\left( {{\mathit{\boldsymbol{y}}_0}} \right) \le G\left( {{\mathit{\boldsymbol{y}}_0}} \right) + \\ C\left( {{\mathit{\boldsymbol{y}}_0}} \right)\left( { - \frac{{G\left( {{\mathit{\boldsymbol{y}}_0}} \right)}}{{C\left( {{\mathit{\boldsymbol{y}}_0}} \right)}}} \right) = 0. \end{array} $ |
Therefore,
| $ v\left( {{\mathit{\boldsymbol{y}}_0}} \right) \ge - \frac{{G\left( {{\mathit{\boldsymbol{y}}_0}} \right)}}{{C\left( {{\mathit{\boldsymbol{y}}_0}} \right)}} \Rightarrow \dot V\left( {{\mathit{\boldsymbol{x}}_0}} \right) \le 0. $ |
In the above three cases it is obtained that
| $ \dot V\left( {{\mathit{\boldsymbol{x}}_0}} \right) \le 0,\forall \mathit{\boldsymbol{x}} \in X. $ |
In conclusion, the derivative with respect to time of the Lyapunov function candidate,
Because y=Qx, from the condition 3) we know that set
The conditions 1) and 2) in Theorem 2.1 guarantee that the function
The stability analysis algorithm ensuring the stability of the systems with forced term is based on Theorem 2.1. It consists of five steps shown as follows.
1) Give a general upper triangular matrix in which the diagonal elements are positive,
| $ \mathit{\boldsymbol{Q = }}{\left( {\begin{array}{*{20}{c}} {{a_{11}}}& \cdot & \cdot &{{a_{1n}}}\\ {}& \cdot &{}& \cdot \\ {}&{}& \cdot & \cdot \\ {}&{}&{}&{{a_{nn}}} \end{array}} \right)_{n \times n}};{a_{11}}, \cdots ,{a_{nn}} > 0. $ |
2) Transform system (1) to system (2) by the linear transformation y=Qx and determine G(y), C(y) and C0.
3) Apply the undetermined coefficient method to determine the elements of Q by the condition 1) of Theorem 2.1 and then determine C+ and C-.
4) Determine v(y) so that
5) Use the linear transformation y=Qx to find u(x) after v(y) is obtained.
Note that the construction of v(y) is based on personal attempt. However, the verification and complex computations can be implemented on a computer. The specific application of this algorithm will be illustrated in section 6.
3 Stability analysis of Hopf bifur-cations with forced termA discriminant for judging the stability of Hopf bifurcation is presented in this section. The stability analysis of Hopf bifurcation with forced term is based on the discriminant. Consider a system with Hopf bifurcation,
| $ \mathit{\boldsymbol{\dot x = f}}\left( \mathit{\boldsymbol{x}} \right) = \mathit{\boldsymbol{Jx + F}}\left( \mathit{\boldsymbol{x}} \right),\mathit{\boldsymbol{x}} \in {R^n}, $ | (5) |
where J is Jacobian matrix of system (5), f is analytic, F(x)=(f1, f2, …, fn)T.
Note that x=0 is an equilibrium of system (5). The function F and its first-order derivative vanish at x=0. Without loss of generality, we assume that J is Jordan canonical form (otherwise we change J to Jordan canonical form by linear transformation x=Ty). Here, J has a pair of purely imaginary eigenvalues ±iωc at the equilibrium x=0. Without loss of generality, we assume ωc=1 (otherwise one may use an additional transformation t′=ωct to change frequency ωc to 1), and the Jordan canonical form of Jacobian matrix of system (5) at x=0 is
| $ \mathit{\boldsymbol{J = }}\left[ {\begin{array}{*{20}{c}} 0&1&0\\ { - 1}&0&0\\ 0&0&A \end{array}} \right],A \in {R^{\left( {n - 2} \right) \times \left( {n - 2} \right)}}, $ |
where A is hyperbolic. For most of the physical situations, we assume the unstable manifold is empty (the eigenvalues of A only have negative real parts).
To give the following theorem for determining the stability of n-dimensional system conveniently, fk in (5) is written as
| $ \begin{array}{l} {f_1} = {s_{11}}{x_1}^2 + {s_{12}}{x_2}^2 + {s_{13}}{x_1}{x_2} + {s_{14}}{x_1}{x_3} + {s_{15}}{x_2}{x_3} + \\ \;\;\;\;\;\;\;{s_{16}}{x_1}^3 + {f_{11}},\\ {f_2} = {s_{21}}{x_1}^2 + {s_{22}}{x_2}^2 + {s_{23}}{x_1}{x_2} + {s_{24}}{x_1}{x_3} + {s_{25}}{x_2}{x_3} + \\ \;\;\;\;\;\;\;{s_{26}}{x_2}^3 + {f_{21}},\\ {f_k} = {s_{k1}}{x_1}^2 + {s_{k2}}{x_2}^2 + {s_{k3}}{x_1}{x_2} + {f_{k1}},k = 3,4, \ldots ,n, \end{array} $ | (6) |
where f11 does not contain terms like x12, x22, x1x2, x1x3, x2x3, x13, f21 does not contain terms like x12, x22, x1x2, x1x3, x2x3, x23, and fk1 does not contain terms like x12, x22, x1x2.
Theorem 3.1 For system (5), if Δ < 0, then the system will be unstable at the origin; if Δ>0, then the system will be asymptotically stable at the origin. Δ is given by the following formula,
| $ \begin{array}{l} \Delta = \sum\limits_{i = 1}^n {\left( {\frac{1}{2}{\xi _{i2}}{B_{i2}} - {\xi _{i1}}\left( {{B_{i0}} + \frac{1}{2}{B_{i1}}} \right)} \right)} + \\ \;\;\;\;\;\;\sum\limits_{j = 1}^n {\left( {\frac{1}{2}{\tau _{j1}}{B_{j2}} - {\tau _{j2}}\left( {{B_{j0}} - \frac{1}{2}{B_{j1}}} \right)} \right)} + \\ \;\;\;\;\;\;\frac{1}{2}\left( {{B_{22}}{\xi _{22}} + {B_{12}}{\tau _{11}}} \right) - \left( {{B_{10}} + \frac{1}{2}{B_{11}}} \right){\xi _{11}} - \\ \;\;\;\;\;\;\left( {{B_{20}} - \frac{1}{2}{B_{21}}} \right){\tau _{22}} - \frac{3}{4}\left( {{s_{16}} + {s_{26}}} \right), \end{array} $ | (7) |
where ξi1 and ξi2 are the coefficients before x1xi and x2xi in f1, respectively, τj1 and τj2 are the coefficients before x1xj and x2xj in f2, respectively,
| $ {B_{10}} = \frac{{{s_{21}} + {s_{22}}}}{2},{B_{11}} = \frac{{{s_{22}} + 2{s_{13}} - {s_{21}}}}{6}, $ |
| $ {B_{12}} = \frac{{{s_{23}} + 2{s_{11}} - 2{s_{12}}}}{6}, $ |
| $ {B_{20}} = - \frac{{{s_{11}} + {s_{12}}}}{2},{B_{21}} = \frac{{2{s_{23}} + {s_{11}} - {s_{12}}}}{6}, $ |
| $ {B_{22}} = \frac{{2{s_{21}} - 2{s_{22}} - {s_{13}}}}{6}, $ |
| $ {B_{a0}} = \frac{1}{{{\alpha _1}}}{B_{a + 1,0}} + \frac{{{s_{a1}} + {s_{a2}}}}{{2{\alpha _1}}}, $ |
| $ {B_{a1}} = \frac{{{\alpha _1}{B_{a + 1,1}} - 2{B_{a + 1,2}}}}{{a_1^2 + 4}} + \frac{{{\alpha _1}{s_{a1}} - {\alpha _1}{s_{a2}} + 2{s_{a3}}}}{{2\left( {a_1^2 + 4} \right)}}, $ |
| $ {B_{a2}} = \frac{{2{B_{a + 1,1}} - {\alpha _1}{B_{a + 1,2}}}}{{a_1^2 + 4}} + \frac{{2{s_{a1}} - 2{s_{a2}} + {\alpha _1}{s_{a3}}}}{{2\left( {a_1^2 + 4} \right)}}, $ |
| $ a = 3,4, \cdots ,{k_1} + 2, $ |
| $ {B_{b0}} = \frac{{{s_{a1}} + {s_{a2}}}}{{2{\alpha _1}}},{B_{b1}} = \frac{{{\alpha _1}{s_{b1}} - {\alpha _1}{s_{b2}} + 2{s_{b3}}}}{{2\left( {a_1^2 + 4} \right)}}, $ |
| $ {B_{b2}} = \frac{{2{s_{b1}} - 2{s_{b2}} - {\alpha _3}{s_{b3}}}}{{2\left( {\alpha _1^2 + 4} \right)}},b = {k_1} + 3, \cdots ,{k_2} + 2, $ |
| $ {B_{p0}} = \frac{{{s_{p1}} + {s_{p2}}}}{{2{\alpha _p}}},{B_{p1}} = \frac{{{\alpha _p}{s_{p1}} - {\alpha _p}{s_{p2}} + 2{s_{{p_3}}}}}{{2\left( {\alpha _p^2 + 4} \right)}}, $ |
| $ {B_{p2}} = \frac{{2{s_{p1}} - 2{s_{p2}} - {\alpha _3}{s_{p3}}}}{{2\left( {\alpha _p^2 + 4} \right)}},p = {k_2} + 3, \cdots ,{k_3}, $ |
| $ \begin{array}{l} {B_{c0}} = \frac{{\alpha {B_{c + 2,0}} + \omega {B_{c + 3,0}}}}{{{\omega ^2} + {\alpha ^2}}} + \\ \;\;\;\;\;\;\;\;\;\frac{{\alpha \left( {{s_{c1}} + {s_{c2}}} \right) + \omega \left( {{s_{c + 1,1}},{s_{c + 1,2}}} \right)}}{{2\left( {{\omega ^2} + {\alpha ^2}} \right)}}, \end{array} $ |
| $ {B_{c1}} = \frac{{ - 4\alpha {v_{c2}} + \left( {{\alpha ^2} + {\omega ^2} - 4} \right){v_{c1}}}}{{16{\alpha ^2} + {{\left( {{\alpha ^2} + {\omega ^2} - 4} \right)}^2}}}, $ |
| $ {B_{c2}} = \frac{{4\alpha {v_{c1}} + \left( {{\alpha ^2} + {\omega ^2} - 4} \right){v_{c2}}}}{{16{\alpha ^2} + {{\left( {{\alpha ^2} + {\omega ^2} - 4} \right)}^2}}}, $ |
| $ \begin{array}{l} {v_{c1}} = 2{B_{c + 2,2}} + \omega {B_{c + 3,1}} + \alpha {B_{c + 2,1}} - {s_{c3}} + \\ \;\;\;\;\;\;\;\frac{{\alpha \left( {{s_{c1}} - {s_{c2}}} \right) + \omega \left( {{s_{c + 1,1}} - {s_{c + 1,2}}} \right)}}{2}, \end{array} $ |
| $ \begin{array}{l} {v_{c2}} = - 2{B_{c + 2,1}} + \omega {B_{c + 3,2}} + \alpha {B_{c + 2,2}} + {s_{c2}} - \\ \;\;\;\;\;\;\;\;{s_{c1}} - \frac{1}{2}\left( {\alpha {s_3} + \omega {s_{c + 1,3}}} \right), \end{array} $ |
| $ \begin{array}{l} {B_{c + 1,0}} = \frac{{\alpha {B_{c + 3,0}} - \omega {B_{c + 2,0}}}}{{{\omega ^2} + {\alpha ^2}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\frac{{\alpha \left( {{s_{c + 1,1}} + {s_{c + 1,2}}} \right) - \omega \left( {{s_{c1}} + {s_{c2}}} \right)}}{{2\left( {{\omega ^2} + {\alpha ^2}} \right)}}, \end{array} $ |
| $ {B_{c + 1,1}} = \frac{1}{\omega }\left( {2{B_{c2}} + \alpha {B_{c1}} - {B_{c + 2,1}} - \frac{{{s_{c1}} - {s_{c2}}}}{2}} \right), $ |
| $ {B_{c + 1,2}} = \frac{1}{\omega }\left( { - 2{B_{c1}} + \alpha {B_{c2}} - {B_{c + 2,2}} + \frac{1}{2}{s_{c3}}} \right), $ |
| $ c = {k_3} + 1,{k_3} + 3, \cdots ,{k_4} - 1, $ |
| $ {B_{d0}} = \frac{{\omega \left( {{s_{d + 1,1}} + {s_{d + 1,2}}} \right) + \alpha \left( {{s_{d1}} + {s_{d2}}} \right)}}{{2\left( {{\omega ^2} + {\alpha ^2}} \right)}}, $ |
| $ {B_{d1}} = \frac{{ - 4\alpha {u_{d2}} + \left( {{\alpha ^2} - {\omega ^2} - 4} \right){u_{d1}}}}{{16{\alpha ^2} + {{\left( {{\alpha ^2} - {\omega ^2} - 4} \right)}^2}}}, $ |
| $ {B_{d2}} = \frac{{4\alpha {u_{d1}} + \left( {{\alpha ^2} - {\omega ^2} - 4} \right){u_{d2}}}}{{16{\alpha ^2} + {{\left( {{\alpha ^2} + {\omega ^2} - 4} \right)}^2}}}, $ |
| $ {u_{d1}} = - {s_{d3}} + \frac{{\alpha \left( {{s_{d1}} - {s_{d2}}} \right) + \omega \left( {{s_{d + 1,1}} - {s_{d + 1,2}}} \right)}}{2}, $ |
| $ {u_{d2}} = {s_{d2}} - {s_{d1}} - \frac{1}{2}\left( {\alpha {s_{d3}} + \omega {s_{d + 1,3}}} \right), $ |
| $ {B_{d + 1,0}} = \frac{{ - \omega \left( {{s_{d1}} + {s_{d2}}} \right) + \alpha \left( {{s_{d + 1,1}} + {s_{d + 1,2}}} \right)}}{{2\left( {{\omega ^2} + {\alpha ^2}} \right)}}, $ |
| $ {B_{d + 1,1}} = \frac{1}{\omega }\left( { - 2{B_{d1}} + \alpha {B_{d2}} + \frac{1}{2}{s_{d3}}} \right), $ |
| $ \begin{array}{l} {B_{d + 1,2}} = \frac{1}{\omega }\left( {2{B_{d2}} + \alpha {B_{d1}} - \frac{{{s_{d1}} - {s_{d2}}}}{2}} \right),d = {k_4} + 1,\\ {k_4} + 3, \cdots ,{k_5} - 1, \end{array} $ |
| $ {B_{q0}} = \frac{{{\omega _q}\left( {{s_{q + 1,1}} + {s_{q + 1,2}}} \right) + {\alpha _q}\left( {{s_{q1}} + {s_{q2}}} \right)}}{{2\left( {\omega _q^2 + \alpha _q^2} \right)}}, $ |
| $ {B_{q1}} = \frac{{ - 4{\alpha _q}{u_{q2}} + \left( {\alpha _q^2 + \omega _q^2 - 4} \right){u_{q1}}}}{{16\alpha _q^2 + {{\left( {\alpha _q^2 + \omega _q^2 - 4} \right)}^2}}}, $ |
| $ {B_{q2}} = \frac{{4{\alpha _q}{u_{q1}} + \left( {\alpha _q^2 + \omega _q^2 - 4} \right){u_{q2}}}}{{16\alpha _q^2 + {{\left( {\alpha _q^2 + \omega _q^2 - 4} \right)}^2}}}, $ |
| $ {u_{q1}} = - {s_{q3}} + \frac{{{\alpha _q}\left( {{s_{q1}} - {s_{q2}}} \right) + {\omega _q}\left( {{s_{q + 1,1}} - {s_{q + 1,2}}} \right)}}{2}, $ |
| $ {u_{q2}} = {s_{q2}} - {s_{q1}} - \frac{1}{2}\left( {{\alpha _q}{s_{q3}} + {\omega _q}{s_{q + 1,3}}} \right), $ |
| $ {B_{q + 1,0}} = \frac{{ - {\omega _q}\left( {{s_{q1}} + {s_{q2}}} \right) + {\alpha _q}\left( {{s_{q + 1,1}} + {s_{q + 1,2}}} \right)}}{{2\left( {\omega _q^2 + \alpha _q^2} \right)}}, $ |
| $ {B_{q + 1,1}} = \frac{1}{{{\omega _q}}}\left( { - 2{B_{q1}} + {\alpha _q}{B_{q2}} + \frac{1}{2}{s_{q3}}} \right), $ |
| $ {B_{q + 1,2}} = \frac{1}{{{\omega _q}}}\left( {2{B_{q2}} + {\alpha _q}{B_{q1}} - \frac{{{s_{q1}} - {s_{q2}}}}{2}} \right), $ |
| $ q = {k_5} + 1,{k_5} + 3, \cdots ,n - 1. $ |
Proof The normal form of system (5) was given in Refs.[16-17] as follows,
| $ \begin{array}{l} \dot r = {D_2}r + {D_4}r + {D_6}r + \cdots + {D_{2n}}r + \cdots \\ \;\;\; = {a_{13}}{r^3} + {a_{15}}{r^5} + {a_{17}}{r^7} + \cdots + {a_{1\left( {2n + 1} \right)}}{r^{2n + 1}} + \cdots ,\\ \dot \theta = 1 + {D_2}\varphi + {D_4}\varphi + {D_6}\varphi + \cdots + {D_{2n}}\varphi + \cdots \\ \;\;\; = 1 + {a_{23}}{r^2} + {a_{25}}{r^4} + {a_{27}}{r^6} + \cdots + {a_{2\left( {2n + 1} \right)}}{r^{2n}} + \cdots . \end{array} $ | (8) |
Note that the stability of system (5) is the same as system (8).
Hence we need to solve a13, because a13r3=D2r. It is known that the next work is to solve D2r.
We use perturbation analysis method. We begin by introducing new independent variables according to
| $ {T_k} = {\varepsilon ^k}t,k = 0,1,2, \cdots . $ |
Then
| $ \begin{array}{l} \frac{{\rm{d}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}{T_0}}}{{{\rm{d}}t}}\frac{\partial }{{\partial {T_0}}} + \frac{{{\rm{d}}{T_1}}}{{{\rm{d}}t}}\frac{\partial }{{\partial {T_1}}} + \frac{{{\rm{d}}{T_2}}}{{{\rm{d}}t}}\frac{\partial }{{\partial {T_2}}} + \cdots \\ \;\;\;\;\; = {D_0} + \varepsilon {D_1} + \varepsilon {D_2} + \cdots , \end{array} $ | (9) |
where the differential operator Dk=∂/∂Tk.
Then, suppose that the solution of (5) in the neighborhood of x=0 is represented by an expansion of the form
| $ \begin{array}{l} {x_i}\left( {t;\varepsilon } \right) = \varepsilon {x_{i1}}\left( {{T_0},{T_1}, \cdots } \right) + {\varepsilon ^2}{x_{i2}}\left( {{T_0},{T_1}, \cdots } \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\; \cdots ,\left( {i = 1,2,3} \right). \end{array} $ | (10) |
Note that the perturbation parameter ε used in (10) is the same as that used in the time scales Tk=εkt(k=0, 1, 2, …). Substituting (9) and (10) into (5) and balancing the like powers of ε results in the ordered perturbation equations. In the ε1-order perturbation equations, we get
| $ \begin{array}{l} D_0^2{x_{11}} + {x_{11}} = 0,\\ {x_{11}} = r\left( {{T_1},{T_2}, \cdots } \right)\cos \left[ {{T_0} + \varphi \left( {{T_1},{T_2}, \cdots } \right)} \right]\\ \;\;\;\;\; = r\cos \theta ,\\ {x_{21}} = {D_0}{x_{11}} = - r\left( {{T_1},{T_2}, \cdots } \right)\sin \left[ {{T_0} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\varphi \left( {{T_1},{T_2}, \cdots } \right)} \right] = - r\sin \theta . \end{array} $ |
In the ε2-order perturbation equation, we find that xi2 has the form
| $ {x_{i2}} = {B_{i0}} + {B_{i1}}\cos 2\theta + {B_{i2}}\sin 2\theta ,i = 1,2, \cdots ,n. $ | (11) |
In the ε3-order perturbation equation, by eliminating the possible secular term in x13, we get D2r. From the first two equations in the ε3-order perturbation equations,
| $ \begin{array}{l} {D_0}{x_{13}} + {D_1}{x_{12}} + {D_2}{x_{11}} = {x_{23}} + {f_{13}},\\ {D_0}{x_{23}} + {D_1}{x_{22}} + {D_2}{x_{21}} = - {x_{13}} + {f_{23}}, \end{array} $ | (12) |
we obtain
| $ \begin{array}{l} D_0^2{x_{13}} + {x_{13}} = - {D_0}{D_1}{x_{12}} - {D_0}{D_2}{x_{11}} - {D_1}{x_{22}} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{D_2}{x_{21}} + {f_{23}} + {D_0}{f_{13}}. \end{array} $ |
Substituting x11 and x21 into the above equation, we obtain
| $ \begin{array}{l} D_0^2{x_{13}} + {x_{13}} = 2\left( {{D_2}r \cdot \sin \theta + r{D_2}\varphi \cdot \cos \theta } \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{f_{23}} + {D_0}{f_{13}}. \end{array} $ | (13) |
Note that fi3(i=1, 2, …, n) is in terms of x113, x213, x11xi2, x21xi2(i=1, 2, …, n). Because D2r only appears as the coefficient of sinθ, we only need to consider the coefficients before sinθ in f23+D0f13. Thus we only consider the terms like x11xi2, x21xi2, x113(i=1, 2, …, n) in f13, and the terms like x11xi2, x21xi2, x213(i=1, 2, …, n) in f23.
Substituting (11) into (13), we find
| $ \begin{array}{l} D_0^2{x_{13}} + {x_{13}}\\ \; = 2\left( {{D_2}r \cdot \sin \theta + r{D_2}\varphi \cdot \cos \theta } \right) + \\ \;\;\;\;\left[ {\sum\limits_{i = 1}^n {\left( {\frac{1}{2}{\xi _{i2}}{B_{i2}} - {\xi _{i1}}\left( {{B_{i0}} + \frac{1}{2}{B_{i1}}} \right)} \right)} + } \right.\\ \;\;\;\;\sum\limits_{j = 1}^n {\left( {\frac{1}{2}{\tau _{j1}}{B_{j2}} - {\tau _{j2}}\left( {{B_{j0}} - \frac{1}{2}{B_{j1}}} \right)} \right)} + \\ \;\;\;\;\frac{1}{2}\left( {{B_{22}}{\xi _{22}} + {B_{12}}{\tau _{11}}} \right) - \left( {{B_{10}} + \frac{1}{2}{B_{11}}} \right){\xi _{11}} - \\ \;\;\;\;\left. {\left( {{B_{20}} - \frac{1}{2}{B_{21}}} \right){\tau _{22}} - \frac{3}{4}\left( {{s_{16}} + {s_{26}}} \right)} \right]{r^3}\sin \theta + g. \end{array} $ | (14) |
where g does not contain terms like sinθ.
To eliminate the possible secular term in x13 in the right part of (14), it is required that the coefficients of sinθ and cosθ equal 0, which in turn yields
| $ \begin{array}{l} {D_2}r = - \frac{1}{2}{r^3}\left[ {\sum\limits_{i = 1}^n {\left( {\frac{1}{2}{\xi _{i2}}{B_{i2}} - {\xi _{i1}}\left( {{B_{i0}} + \frac{1}{2}{B_{i1}}} \right)} \right)} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\sum\limits_{j = 1}^n {\left( {\frac{1}{2}{\tau _{j1}}{B_{j2}} - {\tau _{j2}}\left( {{B_{j0}} - \frac{1}{2}{B_{j1}}} \right)} \right)} + \\ \;\;\;\;\;\;\;\;\;\;\frac{1}{2}\left( {{B_{22}}{\xi _{22}} + {B_{12}}{\tau _{11}}} \right) - \left( {{B_{10}} + \frac{1}{2}{B_{11}}} \right){\xi _{11}} - \\ \;\;\;\;\;\;\;\;\;\;\left. {\left( {{B_{20}} - \frac{1}{2}{B_{21}}} \right){\tau _{22}} - \frac{3}{4}\left( {{s_{16}} + {s_{26}}} \right)} \right]. \end{array} $ | (15) |
Thus the next work is to get Bi0, Bi1, and Bi2 and solve xi2 in the ε2-order perturbation equations. By using the method of harmonic balancing, we get B10, B11, B12, B20, B21, B22, x12, x22 and Bj0, Bj1, Bj2(j=3, 4, …, n) in the ε2-order perturbation equations.
Finally, we find that a13=-
In system (8), if a13>0, (Δ < 0), then the system is unstable at the origin; if a13 < 0, (Δ>0), then the system is asymptotically stable at the origin. Because systems (8) and (5) have the same stability properties at the origin, thus Theorem 3.1 is obtained.
Remark Considering the length of this article, a brief proof is given here. More detailed proof and relevant details are given in our other papers and in Refs.[16-17].
Consider a general Hopf bifurcation with forced term expressed in terms of (16),
| $ \mathit{\boldsymbol{\dot x = J}}\left( \mathit{\boldsymbol{x}} \right) + \mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{x}} \right) + \mathit{\boldsymbol{b}}\left( \mathit{\boldsymbol{x}} \right)u\left( \mathit{\boldsymbol{x}} \right), $ | (16) |
where J(x) and F(x) meet the conditions described in (5), b(x)=(b1(x), b2(x), …., bn(x)T, and u(x) is a scalar function.
Corollary 3.1 Suppose that x=0 is an equilibrium point of system (16). If the following conditions hold:
1) Jacobian matrix of system (16) has a pair of purely imaginary eigenvalues ±iωc at the equilibrium x=0, and the other eigenvalues at the equilibrium x=0 are hyperbolic. In other words, system (16) is the form of Hopf bifurcation,
2) The discriminant Δ of (16) solved based on Theorem 3.1 is positive. Then u(x) can be found for a given b(x) to make system (16) asymptotically stable at the origin.
The stability analysis algorithm ensuring the stability of the Hopf bifurcation with forced term is based on Corollary 3.1 It consists of the steps given as follows.
1) Assume that u(x)=a0+ax+xTBx+c1x13+c2x23, where
a=(a1, a2, …, an), x=(x1, x2, …, xn)T, and a0, c1, c2, ai(i=1, 2, …, n) are constants, and B is a square matrix of order n.
2) Substitute u(x) in (16), and apply the undetermined coefficient method to determine u(x) by using condition 2) of Corollary 3.1.
3) Check that system (16) with u(x) solved is a Hopf bifurcation, and has an equilibrium x=0. Else go to step 2).
The application of this algorithm will be illustrated in section 6.
4 Further explanation for the stability analysis of systems with forced termIt is easy to find the form of adding forced item in the actual operation by using our two algorithms. For a general system, we can always find u(x) when b(x) has some certain forms. However, sometimes we can not find u(x) when b(x) is given. This is what we need to explain in this section.
Firstly, we show what form b(x) has when u(x) can always be found.
Theorem 4.1 Suppose that x=0 is an equilibrium point of system (1). In system (2), if b(x) is given by b(x)=Ax, where A is a positive or negative definite matrix, then we can find u(x) such that system (2) is globally asymptotically stable in the sense of Lyapunov at the origin.
Proof Based on the algorithm mentioned in section 3, we can prove this theorem easily. We assume that P=I(I is identity matrix) by running step 3) of the algorithm in section 3. Then
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{x}},\dot V\left( \mathit{\boldsymbol{x}} \right) = 2{\mathit{\boldsymbol{y}}^{\rm{T}}}\mathit{\boldsymbol{\dot y = }}2{\mathit{\boldsymbol{y}}^{\rm{T}}}\left( {\mathit{\boldsymbol{f}}\left( \mathit{\boldsymbol{y}} \right) + \mathit{\boldsymbol{Ay}} \cdot v\left( \mathit{\boldsymbol{y}} \right)} \right), $ |
G(y)=2yTf(y), C(y)=2yTAy. If A is a positive definite matrix, then C(x)>0, for x≠0. Hence we get
| $ \begin{array}{l} {C^0} = \left\{ {\mathit{\boldsymbol{y}} \in Y\left| {\mathit{\boldsymbol{y = }}0} \right.} \right\},{C^ + } = \left\{ {\mathit{\boldsymbol{y}} \in Y\left| {\mathit{\boldsymbol{y}} \ne 0} \right.} \right\},\\ {C^ - } = \phi . \end{array} $ |
Then we will find v(y). Because
For example we determine
| $ \begin{array}{l} \mathit{\boldsymbol{c}}\left( \mathit{\boldsymbol{y}} \right)v\left( \mathit{\boldsymbol{y}} \right) = \mathit{\boldsymbol{Ay}} \cdot v\left( \mathit{\boldsymbol{y}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; = \mathit{\boldsymbol{A}} \cdot {\left( {{y_1}v\left( \mathit{\boldsymbol{y}} \right),{y_2}v\left( \mathit{\boldsymbol{y}} \right), \cdots ,{y_n}v\left( \mathit{\boldsymbol{y}} \right)} \right)^{\rm{T}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; = \mathit{\boldsymbol{A}}\left( {{y_1}\left( { - \frac{{{\mathit{\boldsymbol{y}}^{\rm{T}}}f\left( \mathit{\boldsymbol{y}} \right)}}{{{\mathit{\boldsymbol{y}}^{\rm{T}}}\mathit{\boldsymbol{Ay}}}} - \varepsilon } \right),} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{y_2}\left( { - \frac{{{\mathit{\boldsymbol{y}}^{\rm{T}}}{\boldsymbol{f}}\left( \mathit{\boldsymbol{y}} \right)}}{{{\mathit{\boldsymbol{y}}^{\rm{T}}}\mathit{\boldsymbol{Ay}}}} - \varepsilon } \right),\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { \cdots ,{y_n}\left( { - \frac{{{\mathit{\boldsymbol{y}}^{\rm{T}}}{\boldsymbol{f}}\left( \mathit{\boldsymbol{y}} \right)}}{{{\mathit{\boldsymbol{y}}^{\rm{T}}}\mathit{\boldsymbol{Ay}}}} - \varepsilon } \right)} \right). \end{array} $ |
We define A=MTM, z=My, where M is an upper triangular matrix in which the diagonal elements are positive. Hence we assume that
| $ {\mathit{\boldsymbol{M}}^{ - 1}} = \left( {\begin{array}{*{20}{c}} {{m_{11}}}& \cdot & \cdot &{{m_{1n}}}\\ {}& \cdot &{}& \cdot \\ {}&{}& \cdot & \cdot \\ {}&{}&{}&{{m_{nn}}} \end{array}} \right). $ |
Then, from Cauchy-Buniakowsky-Schwarz inequality it results that:
| $ \begin{array}{l} \left\| {{{\left( {{\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{z}}} \right)}^{\rm{T}}}} \right\| = \sqrt {{{\left( {{m_{11}}{z_1} + {m_{12}}{z_2} + \cdots + {m_{1n}}{z_n}} \right)}^2} + \cdots + {{\left( {{m_{nn}}{z_n}} \right)}^2}} \\ \le \sqrt {\left( {m_{11}^2 + \cdots + m_{1n}^2} \right)\left( {z_1^2 + \cdots + z_n^2} \right) + \cdots + m_{nn}^2z_n^2} \\ \le \sqrt {n\left( {m_{11}^2 + \cdots + m_{1n}^2} \right)} \sqrt {\left( {z_1^2 + \cdots + z_n^2} \right)} ,\\ \Rightarrow \left| {{y_i}\left( { - \frac{{{\mathit{\boldsymbol{y}}^{\rm{T}}}\mathit{\boldsymbol{f}}\left( \mathit{\boldsymbol{y}} \right)}}{{{\mathit{\boldsymbol{y}}^{\rm{T}}}\mathit{\boldsymbol{Ay}}}} - \mathit{\boldsymbol{\varepsilon }}} \right)} \right|\\ = \left| {\frac{{{y_i}{\mathit{\boldsymbol{y}}^{\rm{T}}}\mathit{\boldsymbol{f}}\left( \mathit{\boldsymbol{y}} \right)}}{{{\mathit{\boldsymbol{y}}^{\rm{T}}}\mathit{\boldsymbol{Ay}}}} + \mathit{\boldsymbol{\varepsilon }}{y_i}} \right|\\ \le \left| {\frac{{{y_i}{\mathit{\boldsymbol{y}}^{\rm{T}}}\mathit{\boldsymbol{f}}\left( \mathit{\boldsymbol{y}} \right)}}{{{\mathit{\boldsymbol{y}}^{\rm{T}}}\mathit{\boldsymbol{Ay}}}}} \right| + \left| {\mathit{\boldsymbol{\varepsilon }}{y_i}} \right|\\ \le \frac{{\left| {\left( {{m_{ii}}{z_i} + {m_{i\left( {i + 1} \right)}}{z_{i + 1}} + \cdots + {m_{in}}{z_n}} \right) \cdot {{\left( {{\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{z}}} \right)}^{\rm{T}}} \cdot \mathit{\boldsymbol{f}}\left( \mathit{\boldsymbol{y}} \right)} \right|}}{{\left| {{\mathit{\boldsymbol{z}}^{\rm{T}}}\mathit{\boldsymbol{z}}} \right|}} + \left| {\mathit{\boldsymbol{\varepsilon }}{y_i}} \right|\\ \le \frac{{\left| {\left( {{m_{ii}}{z_i} + {m_{i\left( {i + 1} \right)}}{z_{i + 1}} + \cdots + {m_{in}}{z_n}} \right)} \right| \cdot \left\| {{{\left( {{\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{z}}} \right)}^{\rm{T}}}} \right\| \cdot \left\| {\mathit{\boldsymbol{f}}\left( \mathit{\boldsymbol{y}} \right)} \right\|}}{{\left| {{\mathit{\boldsymbol{z}}^{\rm{T}}}\mathit{\boldsymbol{z}}} \right|}} + \left| {\mathit{\boldsymbol{\varepsilon }}{y_i}} \right|\\ \le \frac{{\sqrt {m_{ii}^2 + \cdots + m_{in}^2} \sqrt {z_i^2 + \cdots + z_n^2} \sqrt {n\left( {m_{11}^2 + \cdots + m_{1n}^2} \right)} \sqrt {\left( {z_1^2 + \cdots + z_n^2} \right)} \sqrt {f_1^2 + \cdots + f_n^2} }}{{\left| {{\mathit{\boldsymbol{z}}^{\rm{T}}}\mathit{\boldsymbol{z}}} \right|}} + \left| {\mathit{\boldsymbol{\varepsilon }}{y_i}} \right|\\ \le \frac{{\sqrt {m_{ii}^2 + \cdots + m_{in}^2} \sqrt {n\left( {m_{11}^2 + \cdots + m_{1n}^2} \right)} \sqrt {f_1^2 + \cdots + f_n^2} \left| {{\mathit{\boldsymbol{z}}^{\rm{T}}}\mathit{\boldsymbol{z}}} \right|}}{{\left| {{\mathit{\boldsymbol{z}}^{\rm{T}}}\mathit{\boldsymbol{z}}} \right|}} + \left| {\mathit{\boldsymbol{\varepsilon }}{y_i}} \right|\\ = \sqrt {m_{ii}^2 + \cdots + m_{in}^2} \sqrt {n\left( {m_{11}^2 + \cdots + m_{1n}^2} \right)} \sqrt {f_1^2 + \cdots + f_n^2} + \left| {\mathit{\boldsymbol{\varepsilon }}{y_i}} \right|. \end{array} $ |
Hence c(y)v(y)→0 if y→0.
In conclusion,
If A is a negative definite matrix, the proof is similar. So we say that we can find u(x) such that system (2) is globally asymptotically stable in the sense of Lyapunov at the origin. The proof is now completed.
Next, we give some counterexamples to show that we can not find u(x) for some b(x).
Counterexample 4.1 Consider a system in the form
| $ \left( {\begin{array}{*{20}{c}} {{{\dot x}_1}}\\ {{{\dot x}_2}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{x_1}}\\ {{x_2}} \end{array}} \right). $ | (17) |
Suppose that the forced term is given by
| $ \mathit{\boldsymbol{D}}\left( \mathit{\boldsymbol{x}} \right) = \left( {\begin{array}{*{20}{c}} {{x_1}}\\ { - {x_2}} \end{array}} \right)u\left( \mathit{\boldsymbol{x}} \right) = \mathit{\boldsymbol{b}}\left( \mathit{\boldsymbol{x}} \right)u\left( \mathit{\boldsymbol{x}} \right). $ | (18) |
Then we add the forced term (18) to system (17), and we get a system with forced term as follows,
| $ \left( {\begin{array}{*{20}{c}} {{{\dot x}_1}}\\ {{{\dot x}_2}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{x_1}}\\ {{x_2}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{x_1}}\\ { - {x_2}} \end{array}} \right)u\left( \mathit{\boldsymbol{x}} \right). $ | (19) |
We can not find u(x) so that system (19) is globally asymptotically stable in the sense of Lyapunov at the origin. Next we give the proof.
Proof
| $ \begin{array}{l} \left\{ \begin{array}{l} {{\dot x}_1} = {x_1} + {x_1}u\left( \mathit{\boldsymbol{x}} \right)\\ {{\dot x}_2} = {x_2} - {x_2}u\left( \mathit{\boldsymbol{x}} \right) \end{array} \right. \Rightarrow \left\{ \begin{array}{l} {x_2}{{\dot x}_1} = {x_1}{x_2} + {x_2}{x_1}u\left( \mathit{\boldsymbol{x}} \right)\\ {x_1}{{\dot x}_2} = {x_1}{x_2} - {x_1}{x_2}u\left( \mathit{\boldsymbol{x}} \right) \end{array} \right.\\ \Rightarrow {x_2}{{\dot x}_1} + {x_1}{x_2} = 2{x_1}{x_2} \Rightarrow \frac{{{{\dot x}_1}}}{{{x_1}}} + \frac{{{{\dot x}_2}}}{{{x_2}}} = 2 \Rightarrow \ln {x_1} + \\ \ln {x_2} = 2t + c \Rightarrow \ln {x_1}{x_2} = 2t + c \Rightarrow {x_1}{x_2} = \\ {{\rm{e}}^{2t + c}} = C{{\rm{e}}^{2t}}, \end{array} $ | (20) |
where c and C are constants. Hence we get that x1x2=Ce2t. If system (19) is globally asymptotically stable in the sense of Lyapunov at the origin, then x1(t)→0, x2(t)→0, as t→∞. However, x1x2=Ce2t→∞, as t→∞.
So a contradiction appears. The proof is now complete.
Counterexample 4.2 Consider a system in the form (17), suppose that the forced term is given by
| $ \mathit{\boldsymbol{D}}\left( \mathit{\boldsymbol{x}} \right) = \left( {\begin{array}{*{20}{c}} 1\\ { - 1} \end{array}} \right)u\left( \mathit{\boldsymbol{x}} \right) = \mathit{\boldsymbol{b}}\left( \mathit{\boldsymbol{x}} \right)u\left( \mathit{\boldsymbol{x}} \right). $ | (21) |
Then we add the forced term (21) to system (17), and we get a system with forced term as follows,
| $ \left( {\begin{array}{*{20}{c}} {{{\dot x}_1}}\\ {{{\dot x}_2}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{x_1}}\\ {{x_2}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 1\\ { - 1} \end{array}} \right)u\left( \mathit{\boldsymbol{x}} \right). $ | (22) |
We can not find u(x) so that system (22) is globally asymptotically stable in the sense of Lyapunov at the origin. Next we give the proof.
Proof
| $ \begin{array}{l} \left\{ \begin{array}{l} {{\dot x}_1} = {x_1} + u\left( \mathit{\boldsymbol{x}} \right)\\ {{\dot x}_2} = {x_2} - u\left( \mathit{\boldsymbol{x}} \right) \end{array} \right. \Rightarrow {{\dot x}_1} + {{\dot x}_2} = {x_1} + {x_2} \Rightarrow \\ \frac{{{{\dot x}_1} + {{\dot x}_2}}}{{{x_1} + {x_2}}} = 1 \Rightarrow \ln \left( {{x_1} + {x_2}} \right) = t + c \Rightarrow \\ {x_1} + {x_2} = {{\rm{e}}^{t + c}} = C{{\rm{e}}^t}, \end{array} $ | (23) |
where c and C are constants. Hence we get that x1+x2=Cet. If system (19) is globally asymptotically stable in the sense of Lyapunov at the origin, then x1(t)→0, x2(t)→0, as t→∞. However, x1+x2=Cet→∞, as t→∞.
So a contradiction appears. The proof is now complete.
5 Some examplesThis section is dedicated to the validation of the theoretical results derived in sections 3, 4, and 5.
Firstly, we give a nonlinear system with forced term, the inverted pendulum on a cart system. This simple mechanical system is representative to model a class of attitude control problems, and the goal is to maintain permanently the desired vertically oriented position. Since the inverted pendulum is a nonlinear system, the basic balance equations for the system are derived firstly and put into the standard state-space form. Given an inverted pendulum mounted on a cart as shown in Fig. 1, the first principle nonlinear equations are applied in the sequel. Assuming that the rod is massless and that the cart mass and the point mass at the upper end of the inverted pendulum are denoted as M and m, respectively, the gravity force acts on the point mass at all times. The coordinate system is defined in Fig. 1, where x(t) represents the cart position and θ(t) is the tilt angle with respect to the vertical upward direction.

|
Download:
|
|
Fig. 1 Variables related to the inverted pendulum on a cart system |
|
The differential equation that describes the behavior of the simple system is usually written as
| $ \left( {m + M} \right) \cdot {l^2} \cdot \ddot \theta - \left( {m + M} \right) \cdot l \cdot g \cdot \sin \left( \theta \right) = 0, $ | (24) |
where M is the mass of the cart, m is the mass of the pendulum, l is the length of pendulum (distance to the center of mass), x is the cart position coordinate, and θ is the pendulum angle with respect to the vertical position.
The state vector consists of the angle θ and the angular velocity of the pendulum
In order to write equation (24) in terms of state variables, they are substituted resulting in
| $ \mathit{\boldsymbol{\dot z = f}}\left( \mathit{\boldsymbol{z}} \right), $ | (25) |
where
| $ \mathit{\boldsymbol{\dot z = f}}\left( \mathit{\boldsymbol{z}} \right) + \mathit{\boldsymbol{b}}\left( \mathit{\boldsymbol{z}} \right)u\left( \mathit{\boldsymbol{z}} \right), $ | (26) |
where
| $ \mathit{\boldsymbol{f}}\left( \mathit{\boldsymbol{z}} \right) = \left( {\begin{array}{*{20}{c}} {{z_2}}\\ {\frac{g}{l}\sin {z_1}} \end{array}} \right),\mathit{\boldsymbol{b}}\left( \mathit{\boldsymbol{z}} \right) = \left( {\begin{array}{*{20}{c}} 0\\ { - \frac{1}{{\left( {m + M} \right){l^2}}}} \end{array}} \right). $ |
Note that b(z) is given according to the physical meaning.
The algorithm presented in section 3 will be applied as follows, in order to find the value of u(x) at which system (26) is stabilized.
Step 1: Give a general upper triangular matrix in which the diagonal elements are positive,
| $ \mathit{\boldsymbol{Q = }}\left( {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}\\ {}&{{a_{22}}} \end{array}} \right);\;\;{a_{11}},{a_{22}} > 0. $ |
Step 2: Transform system (26) to system (27) by the linear transformation y=Qx, and get the expressions of G(y), C(y), and C0,
| $ \begin{array}{l} \left( {\begin{array}{*{20}{c}} {{{\dot y}_1}}\\ {{{\dot y}_2}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\frac{{{a_{11}}}}{{{a_{22}}}}{y_2} + \frac{{g{a_{12}}}}{l}\sin \left( {\frac{1}{{{a_{11}}}}{y_1} - \frac{{{a_{12}}}}{{{a_{11}}{a_{22}}}}{y_2}} \right)}\\ {\frac{{g{a_{12}}}}{l}\sin \left( {\frac{1}{{{a_{11}}}}{y_1} - \frac{{{a_{12}}}}{{{a_{11}}{a_{22}}}}{y_2}} \right)} \end{array}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\left( {\begin{array}{*{20}{c}} { - \frac{{{a_{12}}}}{{\left( {m + M} \right){l^2}}}}\\ { - \frac{{{a_{22}}}}{{\left( {m + M} \right){l^2}}}} \end{array}} \right)v\left( y \right), \end{array} $ | (27) |
| $ \begin{array}{l} \dot V\left( \mathit{\boldsymbol{z}} \right) = 2\left( {{y_1}{{\dot y}_1} + {y_2}{{\dot y}_2}} \right)\\ \;\;\;\;\;\;\;\; = 2\left[ {\frac{{{a_{11}}}}{{{a_{12}}}}{y_1}{y_2} + \left( {\frac{g}{l}{a_{12}}{y_1} + \frac{g}{l}{a_{22}}{y_2}} \right) \cdot } \right.\\ \;\;\;\;\;\;\;\;\left. {\sin \left( {\frac{1}{{{a_{11}}}}{y_1} - \frac{{{a_{12}}}}{{{a_{11}}{a_{22}}}}{y_2}} \right)} \right] - \\ \;\;\;\;\;\;\;\;\frac{2}{{\left( {m - M} \right){l^2}}}\left( {{y_1}{a_{12}} + {y_2}{a_{22}}} \right)v\left( \mathit{\boldsymbol{y}} \right), \end{array} $ | (28) |
| $ \begin{array}{l} G\left( \mathit{\boldsymbol{y}} \right) = 2\left[ {\frac{{{a_{11}}}}{{{a_{22}}}}{y_1}{y_2} + \left( {\frac{g}{l}{a_{12}}{y_1} + \frac{g}{l}{a_{22}}{y_2}} \right) \cdot } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {\sin \left( {\frac{1}{{{a_{11}}}}{y_1} - \frac{{{a_{12}}}}{{{a_{11}}{a_{22}}}}{y_2}} \right)} \right], \end{array} $ | (29) |
| $ \begin{array}{l} C\left( \mathit{\boldsymbol{y}} \right) = - \frac{2}{{\left( {m + M} \right){l^2}}}\left( {{y_1}{a_{12}} + {y_2}{a_{22}}} \right),\\ {C^0} = \left\{ {\mathit{\boldsymbol{y}} \in Y\left| {{y_2} = - \frac{{{a_{12}}}}{{{a_{22}}}}{y_1}} \right.} \right\}, \end{array} $ | (30) |
where Y=[-80a11-30a12, 80a11+30a12]×[-30a22, 30a22].
Step 3: Apply the undetermined coefficient method to determine the elements of Q by using condition 1) of Theorem 2.1. The condition is that G(y)≤0 for ∀y∈C0. Next, we substitute
| $ \begin{array}{l} G\left( \mathit{\boldsymbol{y}} \right) = 2\left[ {\frac{{{a_{11}}}}{{{a_{22}}}}{y_1}{y_2} + \left( {\frac{g}{l}{a_{12}}{y_1} + \frac{g}{l}{a_{22}}{y_2}} \right) \cdot } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {\sin \left( {\frac{1}{{{a_{11}}}}{y_1} - \frac{{{a_{12}}}}{{{a_{11}}{a_{22}}}}{y_2}} \right)} \right]\\ \;\;\;\;\;\;\;\;\; = 2\left[ { - \frac{{{a_{11}}{a_{12}}}}{{a_{22}^2}}y_1^2 + \frac{g}{l}\left( {{a_{12}}{y_1} - {a_{12}}{y_1}} \right) \cdot } \right.\\ \;\;\;\;\;\;\;\;\;\left. {\sin \left( {\frac{1}{{{a_{11}}{y_1}}} + \frac{{a_{12}^2}}{{{a_{11}}a_{22}^2}}{y_1}} \right)} \right]\\ \;\;\;\;\;\;\;\;\; - \frac{{2{a_{11}}{a_{12}}}}{{a_{22}^2}}y_1^2. \end{array} $ | (31) |
In order to decrease the complexity, we assume a11=a22=1, a12=0 so that G(y)≤0 for ∀y∈C0. Next, we substitute a11=a22=1, a12=0 into (28), (29), and (30),
| $ \begin{array}{l} \dot V\left( \mathit{\boldsymbol{z}} \right) = 2\left( {{y_1}{{\dot y}_1} + {y_2}{{\dot y}_2}} \right) = 2\left( {{y_1}{y_2} + \frac{g}{l}{y_2}\sin {y_1}} \right) - \\ \;\;\;\;\;\;\;\;\;\;\frac{2}{{\left( {m + M} \right){l^2}}}{y_2}v\left( \mathit{\boldsymbol{y}} \right), \end{array} $ | (32) |
| $ \begin{array}{l} C\left( \mathit{\boldsymbol{y}} \right) = - \frac{2}{{\left( {m + M} \right){l^2}}}{y_2},G\left( \mathit{\boldsymbol{y}} \right) = 2\left( {{y_1}{y_2} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {\frac{g}{l}{y_2}\sin {y_1}} \right),\\ {C^0} = \left\{ {\mathit{\boldsymbol{y}} \in Y\left| {{y_2} = 0} \right.} \right\}, \end{array} $ | (33) |
and we also get
| $ {C^ + } = \left\{ {\mathit{\boldsymbol{y}} \in \mathit{\boldsymbol{Y}}\left| {{y_2} < 0} \right.} \right\},{C^ - } = \left\{ {\mathit{\boldsymbol{y}} \in \mathit{\boldsymbol{Y}}\left| {{y_2} > 0} \right.} \right\}, $ |
where Y=[-80, 80]×[-30, 30].
Step 4: Determine v(y) so that
| $ \begin{array}{l} v\left( \mathit{\boldsymbol{y}} \right) \le - \frac{{G\left( \mathit{\boldsymbol{y}} \right)}}{{C\left( \mathit{\boldsymbol{y}} \right)}} = l\left( {m + M} \right)\left( {{y_1}l + g\sin {y_1}} \right){\rm{for}}\;\mathit{\boldsymbol{y}} \in {C^ + },\\ v\left( \mathit{\boldsymbol{y}} \right) \ge - \frac{{G\left( \mathit{\boldsymbol{y}} \right)}}{{C\left( \mathit{\boldsymbol{y}} \right)}} = l\left( {m + M} \right)\left( {{y_1}l + g\sin {y_1}} \right){\rm{for}}\;\mathit{\boldsymbol{y}} \in {C^ - },\\ c\left( \mathit{\boldsymbol{y}} \right)v\left( \mathit{\boldsymbol{y}} \right) \to 0\;{\rm{for}}\;\mathit{\boldsymbol{y}} \to 0.\;\;{\rm{Thus,}}\;\;{\rm{it}}\;{\rm{can}}\;{\rm{be}}\;{\rm{taken}}\\ \;\;\;\;\;\;\;v\left( \mathit{\boldsymbol{y}} \right) = l = \left( {m + M} \right)\left( {{y_1}l + g\sin {y_1}} \right) + {y_2}. \end{array} $ | (34) |
Step 5: Check that v(y) fulfills condition 3) of Theorem 2.1. By substituting (34) into (32), the derivative is
| $ \begin{array}{l} \dot V\left( \mathit{\boldsymbol{z}} \right) = 2{y_2}\left( {{y_1} + \frac{g}{l}\sin {y_1} - \frac{1}{{\left( {m + M} \right){l^2}}}v\left( \mathit{\boldsymbol{y}} \right)} \right)\\ \;\;\;\;\;\;\;\; = - \frac{2}{{\left( {m + M} \right){l^2}}}y_2^2, \end{array} $ |
with
| $ \begin{array}{l} \frac{{\rm{d}}}{{{\rm{d}}t}}{y_2}\left( t \right) = \frac{g}{l}\sin \left( {{y_1}\left( t \right)} \right) - \frac{1}{{\left( {m + M} \right){l^2}}}v\left( \mathit{\boldsymbol{y}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\; = \frac{g}{l}\sin \left( {{y_1}\left( t \right)} \right) - \frac{1}{{\left( {m + M} \right){l^2}}}.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {l\left( {m + M} \right)\left( {{y_1}l + g\sin {y_1}\left( t \right)} \right) + {y_2}} \right]\\ \;\;\;\;\;\;\;\;\;\;\;\; = - {y_1} - \frac{1}{{\left( {m + M} \right){l^2}}}{y_2} \ne 0, \end{array} $ | (35) |
which means that y2(t) can not stay constant. Hence, y(t)=0 is the only possible state trajectory for which
Step 6: v(y) has been obtained. Find u(z) by using the linear transformation y=Qz, (y=z). Thus, u(z)=l(m+M)(z1l+gsinz1)+z2.
To cnclude, the system with forced term (26) designed here is globally asymptotically stable in the sense of Lyapunov at the origin. Note that u(z) is equal to the externally x-directed force, u=F, which is presented in Fig. 2.
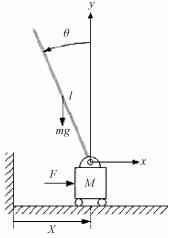
|
Download:
|
|
Fig. 2 Variables related to the inverted pendulum on a cart system with forced term |
|
Next, we consider a system with Hopf bifurcation in the form
| $ \left( {\begin{array}{*{20}{c}} {{{\dot x}_1}}\\ {{{\dot x}_2}}\\ {{{\dot x}_3}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{x_2}}\\ { - {x_1}}\\ { - {x_3}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {x_1^2 + {x_1}{x_2}}\\ {x_1^2}\\ 0 \end{array}} \right). $ | (36) |
For system (36), we find that Δ=-1 < 0. Thus we can know that system (36) is unstable according to Theorem 3.1. Then we will add a forced term to system (36) so that the new system with the forced term is asymptotically stable at the origin. We assume that the new system with forced term is expressed in the form
| $ \left( {\begin{array}{*{20}{c}} {{{\dot x}_1}}\\ {{{\dot x}_2}}\\ {{{\dot x}_3}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{x_2}}\\ { - {x_1}}\\ { - {x_3}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {x_1^2 + {x_1}{x_2}}\\ {x_1^2}\\ 0 \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{b_1}\left( \mathit{\boldsymbol{x}} \right)}\\ {{b_2}\left( \mathit{\boldsymbol{x}} \right)}\\ {{b_3}\left( \mathit{\boldsymbol{x}} \right)} \end{array}} \right)u\left( \mathit{\boldsymbol{x}} \right). $ | (37) |
Without loss of generality, for simplifying the calculation, we assume that bi(x), (i=1, 2, 3) here is given as constant. Thus system (37) is rewritten as follows,
| $ \left( {\begin{array}{*{20}{c}} {{{\dot x}_1}}\\ {{{\dot x}_2}}\\ {{{\dot x}_3}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{x_2}}\\ { - {x_1}}\\ { - {x_3}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {x_1^2 + {x_1}{x_2}}\\ {x_1^2}\\ 0 \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{b_1}}\\ {{b_2}}\\ {{b_3}} \end{array}} \right)u\left( \mathit{\boldsymbol{x}} \right). $ | (38) |
We next find u(x) so that system (38) is asymptotically stable at the origin by our algorithm in section 4. Because the system is simple, we can assume that u(x)=ax12 (a is constant) and substitute u(x) in (38). We apply the undetermined coefficient method to determine u(x) using condition 2) of Corollary 3.1. Based on the calculation, we know that system (38) will be asymptotically stable at the origin, if the following condition holds:
| $ \left( {2{b_2}a + 1} \right)\left( {{b_1}a + 1} \right) < 0. $ | (39) |
Thus, if bi=1, (i=1, 2, 3), we can find u(x)=
We first introduce the system with forced term. Next, an approach to the global asymptotically stability analysis of general system with forced term is proposed. The discrimination method for an n-dimensional system stability is given, and an algorithm to the asymptotically stability analysis of Hopf bifurcation with forced term is developed beased on this discrimination method. Next, a theorem which shows what form of forced term can certainly be found. Some counterexamples, which show that some forms of forced term can not be found for a general system, are given. Some examples show how the stability analysis algorithm suggested here can be applied to systems with forced term. In this study, we give two methods for adding the forced term in theory. Scholars with a wealth of physical knowledge background can further study some specific forms of forced term, which are easy to add for the actual physical problems. Further we will prove that the stability approach in this work can be applied also in situation where the system has an equilibrium point different from the origin.
| [1] | Leine R I. The historical development of classical stability concepts: Lagrange, Poisson and Lyapunov stability[J]. Nonlinear Dynamics, 2010, 59(1/2):173–182. |
| [2] | Bặlaş M M, Bặlaş V E. World Knowledge for control applications by fuzzy-interpolative systems[J]. International Journal of Computers Communications & Control, 2008, 3(1):28–32. |
| [3] | Bazoula A, Djouadi M S, Maaref H. Formation control of multi-robots via fuzzy logic technique[J]. International Journal of Computers Communications & Control, 2008, 3(2):179–184. |
| [4] | Bellomo D, Naso D, Babuška R. Adaptive fuzzy control of a non-linear servo-drive: theory and experimental results[J]. Engineering Applications of Artificial Intelligence, 2008, 21(6):846–857. DOI:10.1016/j.engappai.2007.11.002 |
| [5] | Mohan B M, Sinha A. Analytical structure and stability analysis of a fuzzy PID controller[J]. Applied Soft Computing, 2008, 8(1):749–758. DOI:10.1016/j.asoc.2007.06.003 |
| [6] | Perry A G, Feng G, Liu Y F, et al. A design method for PI-like fuzzy logic controllers for DC-DC converter[J]. IEEE Transactions on Industrial Electronics, 2007, 54(5):2688–2696. DOI:10.1109/TIE.2007.899858 |
| [7] | Vesselenyi T, Dziƫac S, Dziƫac I, et al. Fuzzy and neural controllers for a pneumatic actuator[J]. International Journal of Computers Communications & Control, 2007, 2(4):375–387. |
| [8] | Feng G. A survey on analysis and design of model-based fuzzy control systems[J]. IEEE Transactions on Fuzzy systems, 2006, 14(5):676–697. DOI:10.1109/TFUZZ.2006.883415 |
| [9] | Michels K, Klawonn F, Kruse R, et al. Fuzzy control: fundamentals, stability and design of fuzzy controllers[M]. New York: Springer, 2007. |
| [10] | Precup R E, Preitl S, Rudas I J, et al. Design and experiments for a class of fuzzy controlled servo systems[J]. IEEE/ASME Transactions on Mechatronics, 2008, 13(1):22–35. DOI:10.1109/TMECH.2008.915816 |
| [11] | Tian E, Peng C. Delay-dependent stability analysis and synthesis of uncertain T-S fuzzy systems with time-varying delay[J]. Fuzzy Sets and Systems, 2006, 157(4):544–559. DOI:10.1016/j.fss.2005.06.022 |
| [12] | Khalil H K, Grizzle J W. Nonlinear systems[M]. New Jersey: Prentice Hall, 1996. |
| [13] | Haddad W M, Chellaboina V S. Nonlinear dynamical systems and control: a Lyapunov-based approach[M]. Princeton: Princeton University Press, 2008. |
| [14] | Vidyasagar M. Nonlinear systems analysis[M]. Philadelphia: Society for Industrial & Applied Mathematics (SIAM), 2002. |
| [15] | LaSalle J P. Some extensions of Liapunov's second method[J]. Circuit Theory, IRE Transactions on Circuit Theory, 1960, 7(4):520–527. DOI:10.1109/TCT.1960.1086720 |
| [16] | Yu P. Simplest Normal Forms of Hopf and Generalized Hopf Bifurcations[J]. International Journal of Bifurcation & Chaos, 2011, 9(10):1917–1939. |
| [17] | Yu P. Computation of normal forms via a perturbation technique[J]. Journal of Sound and Vibration, 1998, 211(1):19–38. DOI:10.1006/jsvi.1997.1347 |
 2017, Vol. 34
2017, Vol. 34 


