2. 中国石油工程设计有限公司华北分公司, 河北 任丘 062550;
3. 北京石油化工学院, 北京 102617
2. China Petroleum Engineering Corporation Huabei Branch, Renqiu 062550, Hebei, China;
3. Beijing Institute of Petrochemical Technology, Beijing 102617, China
管道投产是管道由建设施工转入生产运行的关键阶段[1],空管投油[2]是指管道建成后直接进行投油试生产的投产方式,进入管道的液体可能历经分层流、波浪流、气泡流、气团流或段塞流等两相流的流型变化。在实际生产中,长距离输油管道受地形条件的限制而呈现出复杂多变的起伏管路,造成内部呈现气液两相流,且流动参数剧烈波动,不利于投产的安全进行[3]。
目前直接针对起伏管道空管投油的研究较少,但前人在相近领域的研究可为本研究提供参考。宫敬和严大凡[4]基于流体力学原理,分析高程变化较大的管道中,当有不满流存在时管内液流的流动特性。但是,其使用的数学模型只求解了分层流区域的平均持液率,对管道内的流态变化考虑不足,得到结果的应用范围有限。Zhang和Vairavamoorthy[5-6]提出一种针对含气囊管道快速充水瞬变流动过程进行数值求解的数学模型。但该模型只能处理一个气囊的情况,不适用于投产中经常遇到的多气囊问题。针对投油过程中下倾管段常见的滞止气囊,Ha-Ngoc和Fabre[7]提出一种基于边界元法的长气泡形状计算方法,但该方法物理意义不够清晰,并且在编程上难度较大,难以有效地运用到工程实际中。
总体来说,目前对于起伏管道空管投油气液两相流动水力过程的研究还不够充分,对其开展数值模拟研究可为相关研究和工程实践提供一定参考。
1 起伏管道的气液两相流数学模型在投产过程中,地形起伏是影响其水力过程的主要因素。前期使用商业软件FLUENT对局部管段进行的充水过程模拟结果显示,当水头流经处于不同地形的管道时,其流动形态表现出不同的规律。为了对起伏管道内的流场进行实时监测,有效追踪气液两相间的自由界面和捕捉各参数的变化规律,本文基于VOF方法[8]进行数值模拟。下面分别介绍几何模型、数学模型、边界条件和数值方法。
1.1 基本假设实际起伏管道空管投油过程非常复杂,本文基于以下基本假设,对其水力过程进行简化:
1) 不考虑管道横截面形状对水力过程的影响,以二维槽道流动模型模拟实际的三维圆管流动;
2) 管道内的流动介质为水;
3) 不考虑气相与液相之间的物质交换;
4) 气相可压缩,液相不可压缩。
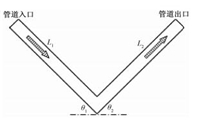
1.2 几何模型建立合理的管道几何模型[9]是进行起伏管道两相流模拟的关键,而模型的尺寸需要结合工程实际情况来确定。本文建立了多种几何模型,这里以V型管道为例,如图 1所示。
|
Download:
|
|
图 1 起伏管道的几何模型示意图 Fig. 1 Schematic of geometric model of hilly pipeline |
|
下倾管段和上倾管段的长度分别为L1和L2,管径为D,倾斜管道与水平线之间的夹角用θ来表示。网格划分采用四边形网格,网格长宽比不超过5。壁面附近速度梯度较大,采用网格加密技术,以准确模拟气液两相流特性。
1.3 控制方程选用VOF模型和RNG k-ε湍流模型,建立求解起伏管道气液两相流问题的数学模型,假设空气为可压缩气体,水为不可压缩液体,气液两相之间不存在质量传递,其控制方程如下。
1) 体积分数的连续性方程:
| $ \frac{\partial }{{\partial t}}\left( {{\alpha _{\rm{g}}}{\rho _{\rm{g}}}} \right) + \nabla \cdot \left( {{\alpha _{\rm{g}}}{\rho _{\rm{g}}}{\mathit{\boldsymbol{v}}_{\rm{g}}}} \right) = 0, $ | (1) |
| $ \frac{\partial }{{\partial t}}\left( {{\alpha _{\rm{l}}}{\rho _{\rm{l}}}} \right) + \nabla \cdot \left( {{\alpha _{\rm{l}}}{\rho _{\rm{l}}}{\mathit{\boldsymbol{v}}_{\rm{l}}}} \right) = 0, $ | (2) |
| $ {\alpha _{\text{g}}} + {\alpha _1} = 1. $ | (3) |
2) 动量方程:
| $ \begin{gathered} \frac{{\partial \left( {\rho \mathit{\boldsymbol{v}}} \right)}}{{\partial t}} + \nabla \cdot \left( {\rho \mathit{\boldsymbol{vv}}} \right) = - \nabla p + \hfill \\ \nabla \cdot \left[ {\mu \left( {\nabla \mathit{\boldsymbol{v + }}\nabla {\mathit{\boldsymbol{v}}^{\rm{T}}}} \right)} \right] + \rho \mathit{\boldsymbol{g + f}}. \hfill \\ \end{gathered} $ | (4) |
3) 能量方程:
| $ \begin{gathered} \frac{\partial }{{\partial t}}\left( {\rho E} \right) + \nabla \cdot \left( {\mathit{\boldsymbol{v}}\left( {\rho E + p} \right)} \right) = \hfill \\ \;\;\;\;\;\;\;\;\;\;\nabla \cdot \left( {{k_{{\rm{eff}}}}\nabla T} \right) + {S_h}. \hfill \\ \end{gathered} $ | (5) |
在整个计算域内,通过求解各相流体的体积分数连续方程,可以追踪气液两相间的界面位置和各相流体所占的体积。对气液两相求解同一套动量方程和能量方程,得到的速度场被气液两相共用,然后根据各相流体体积分数分别求得气液各相的速度等参数值。
4) 湍流方程
| $ \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho k{v_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left( {{\alpha _k}{\mu _{{\rm{eff}}}}\frac{{\partial k}}{{\partial {x_j}}}} \right) + {G_k} + \rho \varepsilon , $ | (6) |
| $ \begin{gathered} \frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho \varepsilon {v_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left( {{\alpha _\varepsilon }{\mu _{{\rm{eff}}}}\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right) + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{{C_{1\varepsilon }^ * \varepsilon }}{k}{G_k} - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k}. \hfill \\ \end{gathered} $ | (7) |
以上连续性方程、动量方程、能量方程和湍流方程共同构成起伏管道空管投油气液两相流问题的控制方程。
1.4 模型参数的确定1) 物性参数
在气液两相流中,研究对象空气和水的物性参数均与温度、压力有关。本文模拟的温度为298.15 K,工作压力为101 325 Pa,根据相关资料[10]查得该状态下空气和水的物性参数如表 1所示。
|
|
表 1 空气和水的物性参数 Table 1 Property parameters of air and water |
2) 湍流参数
在FLUENT软件中,流场的进口和出口边界上需要定义流场的湍流参数。不同的湍流模型中需要设定的湍流参数不同。本文选用的湍流模型为k-ε模型,可以固定湍流动能和湍流耗散率的值。可通过给定水力直径或湍流特征长、湍流强度、湍流动能、湍流耗散率等在边界上的值来定义流场边界上的湍流。
3) 其他参数
纯水在不同温度下的表面张力系数不同,其数值随温度的升高而减小。根据温度和表面张力系数的线性关系可得,298.15 K时的表面张力系数为7.20×10-2 N/m。
1.5 数值计算方法1) 控制方程的离散及求解方法
本文选用非稳态、隐式的分离求解算法,求解的控制方程为满足质量守恒、动量守恒、能量守恒的连续性方程、动量方程、能量方程和考虑湍流性质的湍流方程。采用有限容积法对控制方程进行离散,同时选择合适的离散格式。压力插值格式选择彻体力加权格式;密度、动量、湍流动能、湍流耗散率和能量的插值格式选择一阶迎风格式,稳定性高、计算速度快;体积分数插值格式选择几何重构格式,压力-速度耦合算法选择PISO算法。
2) 边界条件和初始条件
本文模拟的气液两相流中,假设气体是可压缩的,液体不可压缩,可压缩流体的密度随压力降低而减小,体积增大,但质量流量保持不变,因此进口边界条件设为质量入口边界,取值在各算例中说明。出口设为压力出口边界,取值为标准大气压。在边界条件里还可以设定湍流模型的参数,其中的湍流定义方法选择用水力直径和湍流强度,由相关公式求得。VOF方法的计算流程中,还要设置气液界面间的接触角度大小,本文中取为60°。
初始温度取为298.15 K,压力、速度的初场均设为0,湍流动能和湍流耗散率的初值要根据入口质量流量的大小去计算。在初始化面板中,将水的体积分数设为0,在界面上点击Init (初始化) 按钮开始流场的初始化;然后在修补 (Patch) 面板中对水的初始体积分数进行局部修补,以实现管内初始积液高度的设置。
3) 收敛标准
本文中将连续项的残差设为1.0×10-3,速度项的残差为1.0×10-5,能量项的残差为1.0×10-6,湍动能和湍流耗散率项的残差均为1.0×10-3。
2 模拟结果及分析起伏管道有多种组合方式,这里分别模拟V型管道和复杂管道空管投油的气液两相瞬态流动。
2.1 起伏管道的气泡静止条件 2.1.1 气泡静止现象现阶段关于两相流的很多实验及理论模型都是在小管径条件下提出的。本文先选取不同入口流速的小管径短管充水算例,借助V字型管道模拟起伏管道气液两相流动过程中的气泡静止现象。下倾管和上倾管的长度各为0.5 m,直径为50 mm,管道与水平线之间夹角为45°。入口流速分别为2.0、1.2和0.5 m/s时不同时刻的流动状态如图 2所示。

|
Download:
|
|
图 2 不同入口流速下的流动状态 Fig. 2 Flow statuses with varied inlet velocities |
|
观察图 2可见,当入口流速为2.0 m/s和1.2 m/s时,在下倾管段中水流可以持续将气体推向下游,不存在局部存气现象;当入口流速降低到0.5 m/s时,部分气体滞留在下倾管段,形成一个气泡。因此,存在一个能否顺利充水的临界速度。当水流速度大于或等于该临界值时,气体全部流向下游;否则,气体将在下倾管内聚集成气团并处于相对静止的状态,这时只能靠卷吸与输移作用渐渐将气泡排出,用“气泡静止现象”来描述。Kent用“清管临界流速”来定义该速度[11],公式 (系数Co=1.53) 为
| $ \frac{{{V_{\text{C}}}}}{{\sqrt {gD} }} = C_{\text{o}}^{1/2}\sqrt {\sin \theta } . $ | (8) |
为探究工程实际中起伏管道的投产规律是否符合Kent公式,下面分别从管径和倾角的角度,研究气泡静止现象和发生气泡相对静止的临界速度大小。
1) 管径的影响
设定管长为20 m、倾角为45°、初始液位高度为0.5 m、入口流速为1.2 m/s,分别模拟4种不同管径情况下V型管道内的气液两相瞬态流动情况。管径0.394、0.594、0.791和0.981 m时的流动状态如图 3所示。

|
Download:
|
|
图 3 不同管径下的流动状态 Fig. 3 Flow statuses at varied pipe diameters |
|
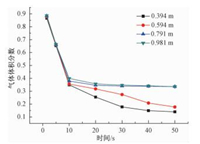
观察图 3可见:在1.5 s时刻,管径越大,水流流到管道底部激起的水花越明显,这是由于在同样的入口流速下,入口流量随管道横截面积的增加而增大;在8.0 s时刻,管径越大,下倾管段末端尚没有水流流至的部分越短;在15.0 s和50.0 s时刻,管径越大,下倾管段内气团的体积越大。不同管径的起伏管道充水过程中气体体积分数随时间的变化曲线如图 4所示。
|
Download:
|
|
图 4 不同管径下管内气体体积分数变化曲线 Fig. 4 Variation curves of volume fraction of gas with time at varied pipeline diameters |
|
在以上4种管径条件下,维持管长20 m、倾角45°、初始液位高度0.5 m不变,入口流速以0.2 m/s为间隔,选取表 2所示9个速度值,记录其气泡运动情况,其中VA为本文模拟得到的临界流速,VC为Kent公式结果。
|
|
表 2 不同管径下的气泡运动情况 Table 2 Moving statuses of the bubbles at varied pipeline diameters |
由表 2可见,临界流速与管径大小正相关。管径越大,其水流临界速度VA值越大。这与Kent计算公式的规律相吻合,但临界速度VA与VC的取值有所不同。显然不能用来预测大管径的临界流速,Kent公式是在小管径实验条件下得到的,要用后面的公式来修正。
2) 倾角的影响
选取管长为20 m,管径为0.791 m,初始液位高度为0.5 m,入口流速分别为1.2、1.4、1.6和1.8 m/s,空气的速度为0,依次将其在20.0 s时刻管内相分布图记录下来。15°、30°和45°这3种倾角下的流动状态如图 5所示。

|
Download:
|
|
图 5 不同倾角下的流动状态 Fig. 5 Flow statuses at varied pipe inclinations |
|
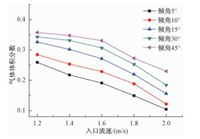
由此发现,以上算例都会在下倾管内出现气泡静止现象,不能顺利完成正常的管道充水过程。倾角越大的下倾管内产生气泡的体积也越大。5°、10°、15°、30°和45°等5种倾角条件下的气体体积分数变化曲线如图 6所示。
|
Download:
|
|
图 6 不同倾角情况下的整管气体体积分数变化曲线 Fig. 6 Variation curves of volume fraction of gas with inlet velocity at varied pipeline inclinations |
|
在以上5种倾角条件下,维持管长20 m、直径0.791 m、初始液位高度0.5 m参数值不变,入口流速以0.1 m/s为间隔,取表 3所示10个速度值,分别记录气泡运动情况。
|
|
表 3 不同倾角条件下的气泡运动情况 Table 3 Moving statuses of the bubbles at varied pipeline inclinations |
由此可知,入口临界流速与倾角大小成正相关,但速度VA与VC取值不同。综合表 2和表 3的各项数据,得到临界流速修正式
| $ {V_{\text{A}}} = \sqrt {{A_{\text{o}}} \cdot \sin \theta \cdot gD + 2.8} . $ | (9) |
此公式中的系数Ao=0.55,其他物理量的含义与式 (8) 相同。
值得说明的是,为减小计算量、提高模拟效率,以上对于起伏管道的模拟,均是在二维模型的基础上进行的。我们还针对典型算例进行了三维模拟,得到管道内不同时刻的体积分数计算结果,与二维模拟结果相似。因此,在本文算例条件下,采用二维模型对该问题进行模拟是可行的。
2.2 复杂管道瞬态水力计算1) 流速的影响
选取长输管道的常用管径0.791 m、管道总长45.1 m和各管倾角均为45°,初始液高为0 m,入口流速分别为2.0、4.0和6.0 m/s,模拟结果如图 7所示。

|
Download:
|
|
图 7 不同入口速度下的流动状态 Fig. 7 Flow statuses at varied inlet velocities |
|
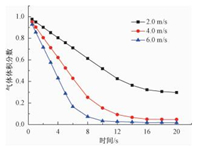
由图 7可知:入口流速为2.0 m/s时,不能顺利完成复杂管道的充水过程;液体流速为4.0和6.0 m/s时,水流能顺利充满管道。不同入口流速下,各时刻复杂管道内气体体积分数值如图 8所示。
|
Download:
|
|
图 8 不同入口流速情况在不同时刻的气体体积分数 Fig. 8 Variation curves of volume fraction of gas with time at varied inlet velocities |
|
由此可见:复杂管道入口流速为2.0 m/s时,管内气体体积分数值只能降低到0.3左右;而入口流速为4.0和6.0 m/s时,管内气体体积分数值可以近似降低到0。
2) 初始条件的影响
为进一步分析复杂管道的充水过程,除入口流速外,还应考虑不同初始条件的影响。定性地,该复杂管道有4种不同初始条件:(a) 空管;(b) 右边有水、左边无水;(c) 左边有水、右边无水;(d) 左右两边都有水。设定积液高度为2.0 m,如图 9所示。

|
Download:
|
|
图 9 初始条件示意图 Fig. 9 Schematic of initial conditions |
|
设定复杂管道的管径为0.791 m,管道总长度为45.1 m,各管道倾角均为45°,水流的入口速度为4.0 m/s,在管道直径、管道总长、倾角和水流速度这4个物理量相等的基础上,分别选择如图 9所示的4种初始条件,得到不同时刻液体体积分数图,如图 10所示。

|
Download:
|
|
图 10 不同初始条件下的流动状态 Fig. 10 Flow statuses under varied initial conditions |
|
由图 10可见,复杂管道内的两相流与初始条件有很大关系,4种初始条件下液体充满整个管道所用的时间也不尽相同:空管条件下,在20.0 s时刻管内气体体积分数为0.048;左边没水、右边有水条件下,在20.0 s时刻管内气体体积分数为0.032;左边有水、右边没水条件下,在20.0 s时刻管内的气体体积分数为0.021;两边都有水条件下,在20.0 s时刻管内的气体体积分数为0.024,此时水流已几乎充满管道。
3 结论1) 通过对V字型管道的模拟,发现产生气泡静止现象的临界流速,其值与管道直径和倾角的大小成正相关,与Kent公式的规律相符合,但模拟得到的临界流速VA与Kent公式结果VC存在偏差。因此实际起伏管道投产过程的顺利与否,可用Kent公式的修正公式来判断,建议投油速度大于临界流速的值。
2) 水平管道的入口流速减小到一定程度时,管内体积最终不能完全被液相所占据。初始液位高度的增加会加剧气液两相间作用,管道内依次出现的流动型态为分层流、泡状流和塞状流等,液体充满管道所用的时间也随之减少。
3) 复杂管道下倾管段内气体的运动方式由入口流速决定。在管道初始液高不为零的情况下,选择不同初始条件会产生不同的两相流现象,管道体积完全被液相占据所需时间也有所不同。
| [1] | 崔岩. 原油长输管线投产运行参数控制与判断[J]. 油气田地面工程, 2010, 29(8):53–54. |
| [2] | 张楠, 宫敬, 闵希华, 等. 大落差对西部成品油管道投产的影响[J]. 油气储运, 2008, 27(1):5–8. |
| [3] | 邱姝娟, 宫敬, 闵希华. 西部原油成品油管道的投产方式[J]. 石油工程建设, 2011, 37(3):35–38. |
| [4] | 宫敬, 严大凡. 大落差管道下坡段不满流流动特性分析[J]. 中国石油大学学报 (自然科学版), 1995, 19(6):65–72. |
| [5] | Zhang Y L, Vairavamoorthy K. Transient flow in rapidly filling air-entrapped pipelines with moving boundaries[J]. Tsinghua Science and Technology, 2006, 11(3):313–323. DOI:10.1016/S1007-0214(06)70195-X |
| [6] | Zhang Y L, Vairavamoorthy K. Application of method-of-lines to charging-up process in pipelines with entrapped air[J]. Tsinghua Science and Technology, 2006, 11(3):324–331. DOI:10.1016/S1007-0214(06)70196-1 |
| [7] | Ha-Ngoc H, Fabre J. A boundary element method for calculating the shape and velocity of two-dimensional long bubble in stagnant and flowing liquid[J]. Engineering Analysis with Boundary Elements, 2006, 30(7):539–552. DOI:10.1016/j.enganabound.2006.02.007 |
| [8] | Hirt C W, Nichols B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39(1):201–225. DOI:10.1016/0021-9991(81)90145-5 |
| [9] | 韩炜.管道气液两相流动技术研究[D].南充:西南石油学院, 2004. |
| [10] | 沈复, 李阳初. 石油加工单元过程原理 (上册)[M]. 北京: 中国石化出版社, 1996: 65-67. |
| [11] | 袁文麒, 刘遂庆. 管道充水工况下气液两相流瞬态数值模拟[J]. 同济大学学报 (自然科学版), 2010, 38(5):709–715. |
 2017, Vol. 34
2017, Vol. 34 


