细颗粒物污染是当下社会普遍高度关注的一个重要的环境问题,对公共健康和经济发展已经造成严重影响。以2013年元月发生在京津冀地区的强霾污染为例,北京地区的小时PM2.5质量浓度一度高达680 μg/m3,当月仅北京市的内科门诊接待病例16 881例,收治急性支气管炎患者10 132例,经济损失高达4.89亿元[1-2]。治理大气细颗粒物污染已迫在眉睫。
细颗粒物的主要排放源有火电厂、建筑工地以及车辆发动机等。工业上采用的细颗粒物脱除技术主要有湿式喷雾除尘和静电除尘等。湿式喷雾除尘简单易操作,成本低,但是对细颗粒物尤其是PM10脱除效果不理想。静电除尘技术对细颗粒物脱除效果显著,但是设备复杂,成本高昂[3]。静电喷雾除尘技术是把湿式除尘与静电除尘相结合,取长补短的一种高效细颗粒物脱除技术,首先由Penney[4]于1944年提出。此后Pilat等[5]研究工业尺度的两级洗涤器的静电喷雾特性,研究结果表明相较于传统喷雾,静电喷雾的除尘效率从68.8%提高到93.6%。Metzler等[6]对旋风除尘器添加二级静电喷雾除尘模块,显著降低了微细颗粒物的脱除效率。这说明静电喷雾对脱除细颗粒物具有独特优势。Balachandran等[7]和Jaworek等[8]分别研究单喷嘴和多喷嘴静电喷雾除尘效率。研究发现雾滴荷电能将除尘效率提高2~4倍。Jaworek等分别在2006年[9]和2013年[10]对静电喷雾研究进行了回顾综述,认为脱除细颗粒物是静电喷雾除尘技术发展的热点方向。
静电喷雾除尘技术具有良好的应用潜力和前景,目前困扰静电喷雾除尘技术应用的一个重要问题是在某些工况下对细颗粒物的脱除效率出现下降。本文利用设计的实验装置研究了细颗粒物撞击荷电液滴过程,对捕集过程中细颗粒物的受力及运动等特性进行分析。
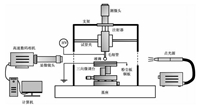
1 实验装置实验装置如图 1所示,注射器配以平头毛细管 (不锈钢材质,外径0.51 mm) 作为液滴发生装置固定在实验台架上,上部利用螺旋微分头精确控制产生的液滴大小,液滴为去离子水。毛细管下方的粉尘板由两层构成,下层为铜板,上层为有机玻璃板,刻有0.5 mm的凹面用来平铺细颗粒物。细颗粒物 (TSI, W.O # 216909, 900890) 为直径10 μm的空心玻璃珠,密度为1 000 kg/m3,具有较高的光反射性。粉尘板由三向微调台托起,精确控制细颗粒物与毛细管间距。毛细管接高压极,电压为1 kV,粉尘板接地。毛细管与粉尘板间距约为2 mm。整个装置固定在水平基座上。利用高速数码相机 (Olympus I-SPEED 3) 配合变焦显微镜头 (NAVITAR 12X) 捕捉细颗粒物运动过程。采用正逆光光源布置形式,以便最大限度减少液滴和颗粒侧面反光干扰。由于拍摄区域非常狭小,拍摄采用点光源 (Olympus ILP-2)。实验环境温度为25 ℃,相对湿度为30%。
|
Download:
|
|
图 1 实验装置示意图 Fig. 1 Schematic of the experimental setup |
|
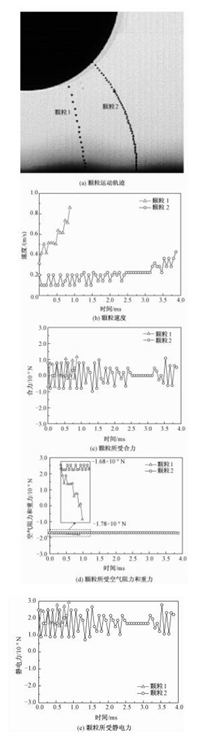
粉尘板上的颗粒荷与液滴相反极性电荷,荷电颗粒与荷电液滴间诱发的静电力驱动其脱离粉尘板向液滴运动,如图 2所示。粉尘板上不同位置荷电颗粒向荷电液滴运动轨迹如图 3(a)所示。作用在颗粒上的静电力与其和荷电液滴之间的距离密切相关,不同的初始脱离位置决定了颗粒所受初始静电力的大小,颗粒所受的静电力由颗粒的运动速度间接体现,如图 3(b)所示。为便于比较,颗粒的初始脱离时间进行了归零处理。颗粒的瞬时运动速度由方程 (1) 计算得出

|
Download:
|
|
图 2 颗粒受荷电液滴吸引脱离粉尘板 Fig. 2 Motion of particles induced by a pendant charged droplet |
|
|
Download:
|
|
图 3 荷电液滴吸附颗粒 Fig. 3 Particle deposit on the surface of the charged droplet |
|
| $ {u_{{\text{p}}i}} = \frac{{{S_i}}}{{\Delta t}}. $ | (1) |
其中,upi为颗粒在图 3(a)中轨迹点i处的瞬时速度,Si是轨迹点i与i-1的间距。Δt是轨迹点采样时间间隔,这里为0.066 7 ms。从图 3(b)中可以明显看出,初始脱离位置离荷电液滴较近的颗粒1的速度更大。
颗粒在气相介质中的运动可以通过牛顿方程进行描述:
| $ \frac{{{\text{d}}{u_{\text{p}}}}}{{{\text{d}}t}} = {f_{\text{D}}}\left( {{u_g} - {u_{\text{p}}}} \right) + \frac{{g\left( {{\rho _g} - {\rho _{\text{p}}}} \right)}}{{{\rho _{\text{p}}}}} + {f_e}. $ | (2) |
其中,ug为气体介质速度,这里ug ≈ 0。g为重力加速度,ρp和ρg分别是颗粒和气体密度,fe为单位颗粒质量所受静电力,fD为单位颗粒质量所受阻力系数。对于不同轨迹点处的颗粒,fD可以表述为
| $ {f_{{\rm{D}}i}} = \frac{{18{\mu _{\rm{g}}}}}{{d_{\rm{p}}^2{\rho _{\rm{p}}}}}\frac{{{C_{{\rm{D}}i}}\mathit{R}{\mathit{e}_i}}}{{24}}, $ | (3) |
其中:μg为气体黏度,CD为曳力系数,Re为颗粒雷诺数,可以表述为
| $ \mathit{R}{\mathit{e}_i} = {\rho _{\rm{g}}}{d_{\rm{p}}}\left| {{u_{{\rm{p}}i}} - {u_g}} \right|/{\mu _g}. $ | (4) |
方程 (2) 左边项为颗粒加速度ap:
| $ {a_{{\text{p}}i}} = \frac{{{u_{{\text{p}}i}} - {u_{{\text{p}}i - 1}}}}{{\Delta t}}. $ | (5) |
由此,颗粒所受的合力可以表述为
| $ {F_{{\text{p}}i}} = {m_{\text{p}}}{a_{{\text{p}}i}}, $ | (6) |
其中,mp为颗粒质量。颗粒1和颗粒2所受合力如图 3(c)所示,颗粒1和颗粒2虽然由于脱离位置不同造成较大的速度差异,但是它们所受的合力基本相同。方程 (2) 右边第1项和第2项分别为颗粒的空气阻力项和重力项,颗粒所受的空气阻力和重力如图 3(d)所示 (不考虑颗粒重力mpg沿速度方向分量变化)。颗粒所受的空气阻力随颗粒速度增大而增大,但是波动范围较小,约为10-10 N。方程 (2) 右边第3项为颗粒所受的静电力项,主要包括库仑力和镜像力等。由于方程 (2) 的其余3项均已获得,因此可以通过计算得出颗粒所受静电力的大小。颗粒所受静电力mpfe如图 3(e)所示,静电力的大小约为 (1~3)×10-9 N。颗粒在气相介质中运动时所受静电力出现明显波动,一方面由于空气阻力干扰,另一方面,可能由吸附空间自由电荷引起。第一,液滴与粉尘板间距很小,实际距离小于1 mm,平均电场强度大于10 kV/cm,虽然没有击穿电流出现,但是空气会出现部分电离;第二,静电场能够加速液滴蒸发[11],液滴蒸发会造成电荷逃逸。颗粒由于吸附相反极性空间自由电荷导致荷电量下降,同时,颗粒不断接近荷电液滴又增强了静电力作用,二者的共同作用致使颗粒所受静电力出现波动。
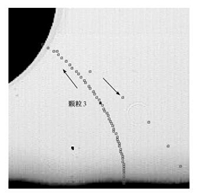
2.2 颗粒的撞击反弹颗粒在经历气相介质中的运动后撞击荷电液滴。值得注意的是,不是所有到达液滴表面的颗粒都被捕集,部分颗粒出现撞击反弹,如图 4所示。颗粒与荷电液滴表面的相互作用决定了其是否会被捕集,这种相互作用主要受颗粒与液滴的相对速度、颗粒的荷电弛豫时间等因素影响。根据Wang等[12]的研究,对于不同颗粒,相对速度在4~10 m/s时颗粒撞击液滴会发生反弹。图 4中颗粒到达液滴表面时速度约为0.23 m/s, 远小于发生反弹的速度范围。根据Sumiyoshitani等[13]的研究,具有较大荷电弛豫时间的颗粒在撞击荷电液滴表面后颗粒净电荷被中和需要一定的时间,这段时间能够延长静电引力对颗粒的吸附作用,促使颗粒被荷电液滴捕集。图 4中颗粒的荷电时间τE=εpε0Pp>3.3 s (其中,εp为颗粒相对介电常数,ε0为真空介电常数,Pp为颗粒电阻率。对于本实验,εp≈3.7,Pp>1011 Ω/m)。因此,颗粒的荷电弛豫时间能够充分延长静电引力作用。但是颗粒仍然出现反弹现象。
|
Download:
|
|
图 4 颗粒反弹 Fig. 4 Rebound of the particle |
|
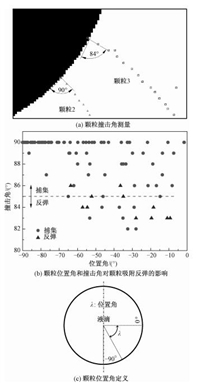
Wang等[11]对颗粒与液滴表面作用动力学行为的研究基于颗粒的垂直撞击,实际上倾斜撞击是更为一般的作用形式。图 4中颗粒3对荷电液滴撞击角的测量结果如图 5(a)所示,颗粒3的撞击角为84°,为倾斜撞击。颗粒倾斜撞击液滴会产生沿液滴表面切向的速度分量,切向速度分量造成的切向颗粒动量能够极大地削弱液滴对颗粒的黏附作用,导致其脱离液滴表面发生反弹。这种现象类似于宏观物体的“打水漂效应”。“打水漂效应”是一种随机事件,可以通过物体对液面的撞击角进行经验性预测。根据Johnson等[14]以及Clanet等[15]的研究,当宏观物体的撞击角小于20°时,有极大概率出现弹跳行为。类似地,本文对到达液滴表面颗粒的撞击角进行了测量,如图 5(b)所示,颗粒的位置角定义如图 5(c)所示。在统计的颗粒中有11% (11/100) 发生了反弹,在反弹的颗粒中,有82% (9/11) 撞击角小于或等于85°。另一方面,在统计的所有颗粒中,有3% (2/82) 的颗粒发生反弹时撞击角大于85°,对应地,有47% (9/19) 的颗粒发生反弹时撞击角小于或等于85°。这说明当颗粒撞击角小于或等于85°时有接近一半的颗粒会发生反弹。同时,从图 5(b)可以看到,当颗粒的位置角小于-70°时反弹基本不会出现,说明荷电液滴表面的这一区域捕集效率最高。
|
Download:
|
|
图 5 颗粒撞击角对颗粒运动特性的影响 Fig. 5 Effect of impact angle on the motion behaviors of the particles |
|
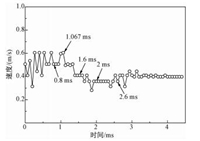
由于静电团聚以及空气湿度等原因,部分颗粒会发生团聚,团聚的颗粒微团受静电力牵引脱离粉尘板向荷电液滴运动。由于颗粒微团结构松散,在撞击荷电液滴时会出现解体,部分子颗粒受库仑斥力影响,脱离液滴表面向周围逃逸,形成细颗粒的二次飞散,如图 6(a)所示。部分颗粒微团在运动过程中始终没有接触到荷电液滴,并最终背向飞离液滴,如图 6(b)所示。一般来说,细颗粒微团的尺寸远大于单个细颗粒,较大的体积和迎风面促使颗粒微团在运动过程中能够吸收更多的空间自由电荷 (这些自由电荷主要来自空气部分电离与液滴蒸发),最终中和自身电荷与荷电液滴保持极性一致,颗粒微团在库仑斥力作用下飞离荷电液滴,完成逃逸过程。颗粒微团在不断吸收空间自由电荷的过程中静电力也会不断下降,导致其速度不断下降,如图 7所示。在大约1~1.5 ms之间细颗粒微团的瞬时速度出现明显下降,此时细颗粒微团的极性已经与荷电液滴相同。

|
Download:
|
|
图 6 颗粒微团的运动 Fig. 6 Motion behaviors of the attracted particle clusters |
|
|
Download:
|
|
图 7 被排斥颗粒微团的速度变化 Fig. 7 Velocity variation of the particle cluster passing the charged droplet |
|
不论被排斥的单分散颗粒还是颗粒微团,它们的极性均与荷电液滴保持一致,因此在实际静电喷雾过程中,这些被排斥的细颗粒物很难再次被其他荷电液滴捕集,造成静电喷雾除尘效率下降。
3 结论利用设计的实验装置对颗粒物撞击荷电液滴进行了实验研究。
对荷电颗粒的受力进行分析。在运动过程中颗粒所受的空气阻力波动较小,其大小比静电力低1个数量级;静电力受颗粒吸附空间自由电荷影响波动较为明显,但总体维持在 (1~3)×10-9N。部分荷电颗粒撞击荷电液滴发生反弹现象。当颗粒的撞击角小于85°时反弹概率接近50%。由于颗粒微团结构松散,在撞击荷电液滴表面后出现二次飞散现象;部分颗粒微团较大的体积和迎风面促使其在运动过程中吸附大量空间电荷,当颗粒微团极性与荷电液滴一致时,诱发的库仑斥力将导致颗粒微团逃逸。
| [1] | 王跃思, 姚利, 王莉莉, 等. 2013年元月我国中东部地区强霾污染成因分析[J]. 中国科学地球科学, 2014, 44(1):15–26. |
| [2] | 谢元博, 陈娟, 李巍. 雾霾重污染期间北京居民对高浓度PM2.5持续暴露的健康风险及其损害价值评估[J]. 环境科学, 2014, 35(1):1–8. |
| [3] | 赵海波.颗粒群平衡模拟的随机模型与燃煤可吸入颗粒物高效脱除的研究[D].武汉:华中科技大学, 2007. |
| [4] | Penney G W. Electrified liquid spray dust precipitator:U S 2357354[P]. 1944. |
| [5] | Pilat M J, Jaasund S A, Sparks L E. Collection of aerosol particles by electrostatic droplet spray scrubbers[J]. Environmental Science and Technology, 1974, 8(4):360–362. DOI:10.1021/es60089a006 |
| [6] | Metzler P, Weiß P, Büttner H, et al. Electrostatic enhancement of dust separation in a nozzle scrubber[J]. Journal of Electrostatics, 1997, 42(1):123–141. |
| [7] | Balachandran W, Jaworek A, Krupa A, et al. Efficiency of smoke removal by charged water droplets[J]. Journal of Electrostatics, 2003, 58(3):209–220. |
| [8] | Jaworek A, Balachandran W, Lackowski M, et al. Multi-nozzle electrospray system for gas cleaning processes[J]. Journal of Electrostatics, 2006, 64(3):194–202. |
| [9] | Jaworek A, Balachandran W, Krupa A, et al. Wet electroscrubbers for state of the art gas cleaning[J]. Environmental Science and Technology, 2006, 40(20):6197–6207. DOI:10.1021/es0605927 |
| [10] | Jaworek A, Krupa A, Sobczyk A T, et al. Submicron particles removal by charged sprays. Fundamentals[J]. Journal of Electrostatics, 2013, 71(3):345–350. DOI:10.1016/j.elstat.2012.11.028 |
| [11] | Takano K, Tanasawa I, Nishio S. Active enhancement of evaporation of a liquid drop on a hot solid surface using a static electric field[J]. International Journal of Heat and Mass Transfer, 1994, 37(94):65–71. |
| [12] | Wang A, Song Q, Yao Q. Behavior of hydrophobic micron particles impacting on droplet surface[J]. Atmospheric Environment, 2015, 115:1–8. DOI:10.1016/j.atmosenv.2015.05.053 |
| [13] | Sumiyoshitani S, Okada T, Hara M, et al. Direct observation of the collection process for dust particles from an air stream by a charged water droplet[J]. IEEE Transactions on Industry Applications, 1984, 20(2):274–281. |
| [14] | Johnson W, Reid S R, Johnson W. Ricochet of spheres off water[J]. Journal of Mechanical Engineering Science, 1975, 17(2):71–81. DOI:10.1243/JMES_JOUR_1975_017_013_02 |
| [15] | Clanet C, Hersen F, Bocquet L. Secrets of successful stone-skipping[J]. Nature, 2004, 427(6969):29. DOI:10.1038/427029a |
 2017, Vol. 34
2017, Vol. 34 


