2. 香港理工大学, 香港 999077
2. The Hong Kong Polytechnic University, Hongkong 999077, China
在深海油气田开发过程中会遇到海底管道的保温问题,常见的保温措施主要包括包裹保温材料和主动加热两种。缺乏有效的保温措施或合适的加热会导致管内油气混合物热量的大量散失与降温,从而导致管内蜡质、沥青质等固态物质的析出,减小管道有效流通面积,严重时甚至堵塞管道,造成生产的中断甚至管线的报废。气-液段塞流是海底油气混输管道中一种常见的流型,目前国内外对无相变冷却条件下气-液段塞流的换热特性研究较少,缺乏可靠的实验数据。
Fried[1]通过实验研究空气-水两相流的压降和换热特性,并在管壁周向上布置热电偶研究管外壁周向温度变化规律。Knott等[2]研究恒定热流密度条件下稠油-氮气混合物的对流换热特性,并提出基于Siedel-Tate关联式[3]的对流换热系数计算模型。Oliver和Wright[4]认为两相流对流换热的强化源自于液相速度的提高以及液塞中漩涡的出现。Dorresteijn[5]通过实验研究加热条件下垂直管路气液两相流对流换热特性,发现当液相流速超过1.0 m/s时,对流换热系数基本不随气相流速的增大而变化。Udeda和Hanaoka[6]研究气液相流速、含气率、液相Pr数等参数对两相流对流换热的影响,发现环状流对流换热系数随含气率的增大显著地增大,段塞流对流换热系数基本不随含气率的变化而变化。
Shoham等[7]研究水平管路气液两相段塞流的对流换热特性,并分析液塞头部、液塞体、液膜区以及长气泡区换热系数的变化规律,发现段塞流上下壁面的对流换热系数明显不同。Hetsroni等[8]采用红外摄像测温技术研究水平管气液两相段塞流对流换热特性,从段塞单元结构的角度分析段塞流对流换热规律,结果表明:段塞流上部对流换热系数受液相流速、长气泡速度、长度、频率等参数的影响较大;段塞流下部对流换热系数基本不受长气泡速度、长度、频率等参数的影响。Franca等[9]在大小两个实验环道中进行冷却条件下段塞流的换热实验,研究无相变冷却条件下段塞流对流换热特性,并分析液塞频率、速度、长度、持液率等液塞参数对段塞流对流换热的影响。
综上所述,目前国内外对冷却条件下段塞流的换热机理研究较少。王鑫等[10]采用环境温度自来水作为冷却液研究段塞流换热特性。本文在此基础上对实验系统进行改进,增加空气加热系统以及冷却液制冷系统,并改进温度测量系统。主要研究无相变冷却条件下段塞流的对流换热特性,并分析气液表观流速、液塞长度、液塞频率以及液膜长度等参数对段塞流对流换热的影响,还研究了段塞流型上下管壁面对流换热的差异。
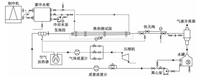
1 实验装置与工况图 1给出水平管气-液两相段塞流对流换热实验系统流程示意图。本实验采用空气和水为实验介质。水储存在容积为1 m3的水罐内,加热后的热流体经离心泵加压,质量流量计计量后进入气液混合器。压缩空气经计量、调节,进入孔眼式气液混合器之前,由气体加热器加热。气液经混合器混合后进入长2 m的水力发展段,段塞流充分发展后进入换热测试段。换热测试段由长4 m,内径0.026 m的紫铜管与内径0.063 m的PVC套管组成,管内热流体与套管中冷却液逆向流动以增大换热,采用T型热电偶测量紫铜管内热流体温度和管外壁温度,采用热电堆测量紫铜管上下壁面温差,采用双平行电导探针测量段塞流的液塞频率、液膜和液塞长度等相界面参数。利用千野公司的Pt100铂电阻 (A级精度:±0.15 ℃) 在恒温水浴中对自制的T型热电偶在实验温度范围内进行了标定。
|
Download:
|
|
图 1 实验流程图 Fig. 1 Schematic of the experimental setup |
|
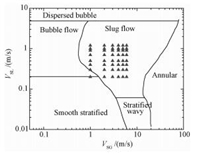
实验中,空气和水的温度取40 ℃,冷却液温度取4 ℃。图 2给出实验工况点在Mandhane流型图上的分布情况,液相表观流速0.3~1.2 m/s,气相表观流速1.1~6.4 m/s。可以看出流型基本全为段塞流,这与实验过程中所观察到的情况一致。
|
Download:
|
|
图 2 实验工况点在Mandhane (1974) 流型图上的分布 Fig. 2 Operating points on Mandhane (1974) flow regime map |
|
换热测试段截面3-4间[10]的管路总换热量Q:
| $ \begin{gathered} Q = \left( {{m_{\text{L}}}{C_{{\text{PL}}}} + {m_{\text{G}}}{C_{{\text{PG}}}}} \right)\Delta {T_{{\text{TP}}}} = \hfill \\ \left( {{V_{{\text{SL}}}}{\rho _{\text{L}}}{C_{{\text{PL}}}} + {V_{{\text{SG}}}}{\rho _{\text{G}}}{C_{{\text{PG}}}}} \right)A\Delta {T_{{\text{TP}}}}, \hfill \\ \end{gathered} $ | (1) |
式中:mG、mL 分别为气、液相质量流量,kg/s;CPG、CPL分别为气、液相的定压比热,kJ/(kg·K);VSG、VSL分别为气、液相表观流速,m/s;A为管道流通截面积,m2;ΔTTP为截面3、4温差,℃,可通过下式计算
| $ \Delta {T_{{\text{TP}}}} = \left( {{T_{{\text{S3f1}}}} + {T_{{\text{S3f2}}}} - {T_{{\text{S4f1}}}} - {T_{{\text{S4f2}}}}} \right)/2. $ | (2) |
式中,Ts3f1、Ts3f2、Ts4f1、Ts4f2分别为截面3、4管内上下两个热电偶测量温度,℃。
管内热流体的定性温度TTP:
| $ {T_{{\text{TP}}}} = \left( {{T_{{\text{S3f1}}}} + {T_{{\text{S3f2}}}} + {T_{{\text{S4f1}}}} + {T_{{\text{S4f2}}}}} \right)/4. $ | (3) |
根据测试段总的换热量守恒原则:
| $ Q = 2\lambda \left( {{T_{{\text{Wi}}}} - {T_{{\text{Wo}}}}} \right)\ln \frac{{{d_i}}}{{{d_o}}}{\text{π}}L = \Delta {T_m}{h_{{\text{TP}}}}{d_i}{\text{π}}L, $ | (4) |
式中:λ为铜管的导热系数,取383.8 W/(m·k);Twi、Two分别为实验管道平均内壁温度和平均外壁温度,℃;di、do分别为实验管道内径和外径,m;L为实验管路长度,m;hTP为两相段塞流对流换热系数,W/(m2·K);ΔTm为内壁面与流体之间的对数平均温差,℃,可根据下式计算:
| $ \Delta {T_m} = \frac{{\left( {{T_{{\text{S4f1}}}} + {T_{{\text{S4f2}}}}} \right) - \left( {{T_{{\text{S3f1}}}} + {T_{{\text{S3f2}}}}} \right)}}{{\ln \left[ {\frac{{{T_{{\text{Wi}}}} - \left( {{T_{{\text{S3f1}}}} + {T_{{\text{S3f2}}}}} \right)/2}}{{{T_{{\text{Wi}}}} - \left( {{T_{{\text{S4f1}}}} + {T_{{\text{S4f2}}}}} \right)/2}}} \right]}}. $ | (5) |
管道内壁面温度Twi根据式 (4) 可得
| $ {T_{{\text{Wi}}}} = {T_{{\text{Wo}}}} + \frac{Q}{{2{\text{π}}\lambda L}}\ln \frac{{{d_{\text{o}}}}}{{{d_{\text{i}}}}}, $ | (6) |
式中,外壁面温度Two根据实验数据平均得到,则两相段塞流对流换热系数hTP:
| $ {h_{{\text{TP}}}} = \frac{Q}{{\Delta {T_m}{\text{π}}{d_i}L}}. $ | (7) |
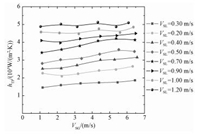
图 3给出段塞流对流换热系数随气相表观流速的变化情况。当液相表观流速较低 (VSL≤0.9 m/s) 时,对流换热系数随气相表观流速的增大略有增大,而当液相表观流速较高 (VSL>0.9 m/s) 时,对流换热系数基本不随气相表观流速的增大而变化。这是因为当液相流速较低时,气相的加入可以有效地增大管内液体的紊流度,减小热边界层的厚度,强化换热;当液相表观流速较高时,管内液体的紊流程度已经较高,气相的加入并不能明显地增大液相的紊流度,对流换热强化不明显。
|
Download:
|
|
图 3 对流换热系数hTP随气相表观速度的变化 Fig. 3 Variation of hTP with superficial gas velocity |
|
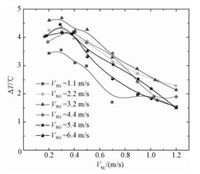
图 4给出上下壁面的温差随液相表观流速的变化情况。本文规定当下壁面温度高时为正。可以看出,下壁面温度明显高于上壁面温度。另外从图 4中可以看出,随着液相表观流速的增大,ΔT不断减小,这是因为当气相流速不变时,随着液相流速的增大,液塞频率增大,流体与上下壁面的换热差异减小,温差减小。
|
Download:
|
|
图 4 上下壁面温差ΔT随液相表观流速的变化 Fig. 4 Variation of ΔT with superficial liquid velocity |
|
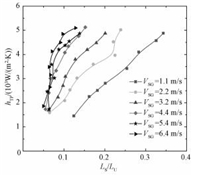
图 5给出段塞流对流换热系数hTP随液塞长度在整个段塞单元中所占比例LS/LU的变化。从图 5可以看出,对流换热系数随LS/LU的增大显著地增大。这是因为液塞区与管壁之间的对流换热明显强于液膜区与管壁之间的对流换热,因此液塞在整个段塞单元中所占的比例越大,换热越强。此外,对流换热系数的增加速度随气相表观流速的增大而增大。
|
Download:
|
|
图 5 对流换热系数hTP随液塞长度的变化 Fig. 5 Variation of hTP with slug length |
|
图 6给出段塞流对流换热系数hTP随液塞频率的变化。可以看出随着液塞频率的增大,对流换热系数显著地增大。这是因为一方面液塞频率的增大意味着单位时间内流过的液塞增多,由于液塞与管壁之间的对流换热系数明显高于液膜区与管壁之间的对流换热系数,因此对流换热系数增大;另一方面,液塞和长气泡交替出现的频率越高,气相对液相的扰动作用也就越强烈,对流换热得到强化。此外,分析还发现,hTP随液塞频率的增长速度随液塞频率的增大而减小,这是因为当液塞频率超过某一值后,气液交替出现的频率足够高,气相对液相的扰动作用对换热的强化作用减弱,导致hTP的增长速度减缓。

|
Download:
|
|
图 6 对流换热系数hTP随液塞频率的变化 Fig. 6 Variation of hTP with slug frequency |
|
图 7给出段塞流对流换热系数hTP随液膜长度的变化。可以看出对流换热系数随液膜长度的增大而显著地减小。一方面液膜速度较慢,内部紊流度较低,液膜与管壁之间的对流换热系数较小;另一方面液膜上部的长气泡与管壁之间的对流换热远低于液相与管壁之间的对流换热,从而导致液膜区与管壁之间的对流换热明显低于液塞区与管壁之间的对流换热,因此随着液膜长度的增大,段塞流对流换热系数迅速减小。

|
Download:
|
|
图 7 对流换热系数hTP随液膜长度的变化 Fig. 7 Variation of hTP with liquid film length |
|
本文在水平实验管路中研究无相变冷却条件下段塞流的换热特性。实验采用电导探针、压差传感器、质量流量计等多种流动参数测试手段以及热电偶、热电阻、热电堆等温度测试手段测量冷却过程中段塞流的流动参数和传热参数,分析段塞流对流换热系数的影响因素以及段塞流的相界面结构特性对换热的影响。
研究发现,段塞流对流换热系数受气相表观流速影响较小。由于液塞与管壁之间的对流换热明显强于液膜区与管壁之间的对流换热,因此对流换热系数随液塞长度占整个段塞单元长度的比例、液塞频率等参数的增大而增大,随液膜长度的增大而减小。
由于管道下壁面始终与液相接触,而上壁面则与气液交替接触,因此流体与下壁面之间的对流换热明显强于流体与上壁面之间的对流换热,因此下壁面温度明显高于上壁面温度,且上下壁面温差随液相表观流速的增大而减小。
| [1] | Fried L. Pressure drop and heat transfer for two-phase, two-component flow[C]//Chem Eng Prog Symp Series, 1954, 50(9):47-51. |
| [2] | Knott R F, Anderson R N, Acrivos A, et al. An experimental study of heat transfer to nitrogen-oil mixtures[J]. Industrial & Engineering Chemistry, 1959, 51(11):1369–1372. |
| [3] | Sieder E N, Tate G E. Heat transfer and pressure drop of liquids in tubes[J]. Industrial & Engineering Chemistry, 1936, 28(12):1429–1435. |
| [4] | Oliver D R, Wright S J. Pressure drop and heat transfer in gas-liquid slug flow in horizontal tubes[J]. British Chemical Engineering, 1964, 9(9):590–596. |
| [5] | Dorresteijn W R. Experimental study of heat transfer in upward and downward two-phase flow of air and oil through 70 mm tubes[C]//Proc 4th Int Heat Transfer Conf, 1970, 5(5-9):1-10. |
| [6] | Ueda T, Hanaoka M. On upward flow of gas-liquid mixtures in vertical tubes:3rd Report, heat transfer results and analysis[J]. Bulletin of JSME, 1967, 10(42):1008–1015. DOI:10.1299/jsme1958.10.1008 |
| [7] | Shoham O, Dukler A E, Taitel Y. Heat transfer during intermittent/slug flow in horizontal tubes[J]. Industrial & Engineering Chemistry Fundamentals, 1982, 21(3):312–319. |
| [8] | Hetsroni G, Yi J H, Hu B G, et al. Heat transfer in intermittent air-water flows.Part Ⅱ:Upward inclined tube[J]. International journal of multiphase flow, 1998, 24(2):189–212. DOI:10.1016/S0301-9322(97)00056-6 |
| [9] | Franca F A, Bannwart A C, Camargo R M T, et al. Mechanistic modeling of the convective heat transfer coefficient in gas-liquid intermittent flows[J]. Heat Transfer Engineering, 2008, 29(12):984–998. DOI:10.1080/01457630802241091 |
| [10] | 王鑫, 徐静静, 祁雷, 等. 水平管空气-水段塞流冷却传热研究[J]. 工程热物理学报, 2014, 35(8):1563–1568. |
 2017, Vol. 34
2017, Vol. 34 


