2. 清华大学核能与新能源技术研究院, 北京 100084
2. Institute of Nuclear and New Energy Technology, Tsinghua University, Beijing 100084, China
在自然环境以及工业领域内,旋转滚筒是气固多相流中的一种典型形式,且因其受环境的影响小,被广泛应用于化工业中的物理和化学过程,如固体混合,颗粒干燥、冷却,煤块粉碎等各种从泥浆状到颗粒状的不同原料的过程工业[1]。因此,旋转滚筒中颗粒状材料混合的研究在过去几年内受到了充分的重视。对这种颗粒流体系统进行数值模拟和定量描述,对于加强颗粒体系微观动力学行为的规律性认识,和其相关工程领域优化操作条件,指导系统设计应用有着重要的理论和现实意义,但由于粒子间强烈且频繁的碰撞及粒子与转动容器壁面间的相互作用导致该过程难以分析[2]。然而研究分析特定条件下混合行为的影响因素的试验性工作是必不可少的,但是由于成本较高且实验结果难以记录等原因,实验只适用于有限情况下。相较而言,数值模拟是一种对具有各种固有物理特性的颗粒在不同条件下产生复杂物理现象进行更好分析的有效途径[3]。
离散元法 (discrete element method, DEM) 被广泛地应用于模拟滚筒中颗粒的运动。已有很多研究人员使用DEM法研究二维和准二维滚筒[4-8],为了更接近于实际工程应用,近年来对于三维滚筒的研究逐渐增多。如Yang等[9]使用DEM法模拟三维滚筒中颗粒的运动,讨论颗粒运动活跃区和相对静止区的关系。Wightman等[10]使用DEM法对摇动及滚动圆柱形容器中颗粒流动和混合进行模拟,发现摇动对颗粒施加了时变扰动,显著增强颗粒混合,并通过实验验证了模拟结果。Sato等[11]采用DEM法模拟不同搅动转速下存在强剪切作用时三维转鼓混合器内的颗粒运动,研究表明颗粒动能可以较好地反映颗粒行为特性。Soni等[12]也使用DEM法模拟填充率高于50%的三维滚筒,发现填充率和颗粒尺寸相对于滚筒转速和几何结构对相对静止区的影响更大[12]。
混合程度是描述和评价旋转滚筒中颗粒运动的一个非常重要的指标,而选取何种混合指数用以评价颗粒的混合程度也是很重要的。常用的评价函数包括Lacey法、Siiriä法、信息熵、配位数、颗粒尺度指数、平均高程法、最近相邻法、邻近距离法、径向分布函数或者这些方法的结合。如Siiriä等[13]提出Siiriä法来评价混合程度,这个方法基于一对颗粒的相对位置随着时间的变化情况。Ayeni等[14]使用基于配位数的信息熵研究不规则形状的滚筒中颗粒混合的情况。Gui等[5-8]对颗粒在圆筒及波形滚筒等不同边界条件下的运动和导热过程进行数值模拟和分析计算,并使用Lacey法、信息熵和径向分布函数分析滚筒操作参数和形状参数对混合伴随的导热过程及颗粒温度场的影响。不同的评价函数其性质有很大差别,在不同方面各有优劣。如Siiriä法复杂性高,受无量纲变量R和比例因子g影响很大,但是具有不受网格划分和颗粒种类变化影响的优良性质[13, 15]。而信息熵可以评价全局的混合程度,与其他混合指数的相容性好,这也导致其形式众多,如基于配位数的信息熵[14]、基于径向分布函数的信息熵[7]等,最为广泛使用的是基于局部浓度的信息熵[15],但它依赖于网格划分和颗粒分类。Wen等[15]对于各种混合指数进行评价和比较,评价指标有复杂度、可否评价多种颗粒多个方向上的混合程度,以及对参数、网格划分方式、颗粒分类方式的依赖度等。
本文借助开源软件OpenFOAM中的DEM软球模型模拟三维滚筒内的颗粒混合,通过新的评价函数对三维滚筒内颗粒混合程度进行研究,定量分析不同滚筒转速对于颗粒混合特性的影响。并将新的评价函数与传统的信息熵方法进行对比验证。
1 数值模型介绍根据牛顿第二定律,DEM完整的控制方程包含颗粒平移运动和颗粒旋转运动两部分,控制方程表达式[16]为:
| $ {m_i}\frac{{{\text{d}}{v_i}}}{{{\text{d}}t}} = \sum\limits_j {F_{ij}^c + F_i^g} , $ | (1) |
| $ {I_i}\frac{{{\text{d}}{w_i}}}{{{\text{d}}t}} = \sum\limits_j {{M_{ij}}} , $ | (2) |
式 (1) 中:mi和vi分别为颗粒的质量和速度;Fijc和Fig分别为颗粒接触力和颗粒所受重力。式 (2) 中:Ii为颗粒的转动惯量;wi和Mij分别为颗粒的角速度和颗粒接触力的转矩。
在Tsuji提出的非线性黏弹性模型[17]中,颗粒接触力的法向力由弹性排斥 (弹簧) 和黏性耗散 (阻尼器) 两部分组成,其公式为
| $ {\mathit{\boldsymbol{F}}^n} = \mathit{\boldsymbol{F}}_{{\rm{et}}}^n + \mathit{\boldsymbol{F}}_{{\rm{diss}}}^n = - {k^n}{\xi ^{3/2}} - {\gamma ^n}\dot \xi {\xi ^{1/4}}, $ | (3) |
其中:Fetn和Fdissn分别代表弹性排斥和黏性耗散;ξ为颗粒碰撞的法向重叠量;
| $ {k^n} = \frac{4}{3}{\left( {\frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}} \right)^{1/2}}{\left( {\frac{{1 - \lambda _1^2}}{{{E_1}}} + \frac{{1 - \lambda _2^2}}{{{E_2}}}} \right)^{ - 1}}, $ | (4) |
式中:R为碰撞颗粒的半径;E为碰撞颗粒的杨氏模量;λ为碰撞颗粒的泊松比。赫兹理论中假设碰撞颗粒表面光滑、接触面为椭球面、不考虑接触面摩擦以及形变为小形变。关于切向接触力模型,本文采取切向力的线性黏弹性模型[19]:
| $ {\mathit{\boldsymbol{F}}^t} = \mathit{\boldsymbol{F}}_{{\rm{et}}}^t + \mathit{\boldsymbol{F}}_{{\rm{diss}}}^t = - {k^t}\beta - {\gamma ^t}\dot \beta , $ | (5) |
式中:β为颗粒碰撞的切向重叠量;
考虑到颗粒与壁面发生滑动的情况,当切向力大于动摩擦力时[20]:
| $ {\mathit{\boldsymbol{F}}^t} = \mu {\mathit{\boldsymbol{F}}^n}, $ | (6) |
其中,μ为液体颗粒与壁面间的摩擦系数。
本文所使用的DEM模型已经在之前的论文[2]中被验证了。
2 模拟工况及函数定义 2.1 模拟工况本文分别模拟5种典型转速下的颗粒运动,即ω=0.5π、1.0π、2.0π、3.0π、4.0π rad/s,模拟参数见表 1。不同速度的初始状况相同,模拟过程采用统一的滚筒尺寸,滚筒半径为0.8 m,截面圆心坐标为原点,z向厚度为0.6 m,所采取的研究思路为:
|
|
表 1 数值模拟参数 Table 1 Simulation parameters |
1) 首先,初始化模拟。先保持滚筒静止,让颗粒在滚筒内自由下落,堆积在滚筒的下半部。
2) 然后定义一个垂直于x轴的oyz平面,将滚筒内的颗粒分为两部分,分别标记颗粒球心位于x=0左右两边为黑颗粒 (a) 和白颗粒 (b),如图 1所示。然后滚筒以设定好的速度开始旋转。

|
Download:
|
|
图 1 初始状态t=0 s时颗粒分布 Fig. 1 Particle distribution at initial time t=0 s |
|
我们在之前的研究中已经使用Lacey法、信息熵和径向分布函数等混合指数[5-8],而本文在评估颗粒混合时使用新的评估函数,即差值函数,定义如下式:
| $ \left\{ \begin{gathered} {x_{{\rm{ab}}}} = \frac{{\sum\limits_{i = 1}^{{N_{\rm{a}}}} {{x_{{\rm{a}},i}}} }}{{{N_{\rm{a}}}}} - \frac{{\sum\limits_{j = 1}^{{N_{\rm{b}}}} {{x_{{\rm{b}},j}}} }}{{{N_{\rm{b}}}}} \hfill \\ {y_{{\rm{ab}}}} = \frac{{\sum\limits_{i = 1}^{{N_{\rm{a}}}} {{y_{{\rm{a}},i}}} }}{{{N_{\rm{a}}}}} - \frac{{\sum\limits_{j = 1}^{{N_{\rm{b}}}} {{y_{{\rm{b}},j}}} }}{{{N_{\rm{b}}}}} \hfill \\ \end{gathered} \right., $ | (7) |
| $ \left\{ \begin{gathered} {u_{{\text{ab}}}} = \frac{{\sum\limits_{i = 1}^{{N_{\text{a}}}} {{u_{{\text{a}},i}}} }}{{{N_{\text{a}}}}} - \frac{{\sum\limits_{j = 1}^{{N_{\text{b}}}} {{u_{{\text{b}},j}}} }}{{{N_{\text{b}}}}} \hfill \\ {v_{{\text{ab}}}} = \frac{{\sum\limits_{i = 1}^{{N_{\text{a}}}} {{v_{{\text{a}},i}}} }}{{{N_{\text{a}}}}} - \frac{{\sum\limits_{j = 1}^{{N_{\text{b}}}} {{v_{{\text{b}},j}}} }}{{{N_{\text{b}}}}} \hfill \\ \end{gathered} \right., $ | (8) |
| $ \left\{ \begin{gathered} {R_{{\rm{ab}}}} = \left[ {{{\left( {\frac{{\sum\limits_{i = 1}^{{N_{\rm{a}}}} {{x_{{\rm{a}},i}}} }}{{{N_{\rm{a}}}}} - \frac{{\sum\limits_{j = 1}^{{N_{\rm{b}}}} {{x_{{\rm{b}},j}}} }}{{{N_{\rm{b}}}}}} \right)}^2} + \left( {\frac{{\sum\limits_{i = 1}^{{N_{\rm{a}}}} {{y_{{\rm{a}},i}}} }}{{{N_{\rm{a}}}}} - } \right.} \right. \hfill \\ {\left. {{{\left. {\frac{{\sum\limits_{j = 1}^{{N_{\rm{b}}}} {{y_{{\rm{b}},j}}} }}{{{N_{\rm{b}}}}}} \right)}^2} + {{\left( {\frac{{\sum\limits_{i = 1}^{{N_{\rm{a}}}} {{z_{{\rm{a}},i}}} }}{{{N_{\rm{a}}}}} - \frac{{\sum\limits_{j = 1}^{{N_{\rm{b}}}} {{z_{{\rm{b}},j}}} }}{{{N_{\rm{b}}}}}} \right)}^2}} \right]^{\frac{1}{2}}} \hfill \\ {U_{{\rm{ab}}}} = \left[ {{{\left( {\frac{{\sum\limits_{i = 1}^{{N_{\rm{a}}}} {{u_{{\rm{a}},i}}} }}{{{N_{\rm{a}}}}} - \frac{{\sum\limits_{i = 1}^{{N_{\rm{b}}}} {{u_{{\rm{b}},j}}} }}{{{N_{\rm{b}}}}}} \right)}^2} + \left( {\frac{{\sum\limits_{i = 1}^{{N_{\rm{a}}}} {{v_{{\rm{a}},i}}} }}{{{N_{\rm{a}}}}} - } \right.} \right. \hfill \\ {\left. {{{\left. {\frac{{\sum\limits_{j = 1}^{{N_{\rm{b}}}} {{v_{{\rm{b}},j}}} }}{{{N_{\rm{b}}}}}} \right)}^2} + {{\left( {\frac{{\sum\limits_{i = 1}^{{N_{\rm{a}}}} {{w_{{\rm{a}},i}}} }}{{{N_{\rm{a}}}}} - \frac{{\sum\limits_{j = 1}^{{N_{\rm{b}}}} {{w_{{\rm{b}},j}}} }}{{{N_{\rm{b}}}}}} \right)}^2}} \right]^{\frac{1}{2}}} \hfill \\ \end{gathered} \right., $ | (9) |
上式中:下标a、b分别代表颗粒种类的编号,Na和Nb分别代表a、b颗粒的个数;x,y,z分别代表颗粒位置坐标;u,v,w则分别为x,y,z方向的速度;xab,yab,uab、vab、Rab和Uab分别定义为a,b两种颗粒在x方向的位置平均差值、y方向的位置平均差值,x方向的速度平均差值、y方向的速度平均差值,平均位置差和平均速度差。
差值函数的物理意义是颗粒a、b在某一方向上平均位置或速度的差值。其值越接近于0,说明在这个方向上的混合程度越好。
为了对比验证差值函数的正确性,本文引入信息熵函数。类似于热力学熵描述分子状态混乱程度,香农信息熵可以用来描述信源的不确定度[21]。信息熵的值与混合程度呈正相关。因此,信息熵被广泛应用于表征颗粒混合程度从而量化分析颗粒混合程度与滚筒转速、混合时间的关系[5-6, 8, 14, 22]。如前言所述,信息熵形式众多,为了对比验证本文提出的新的评价函数,采用基于局部浓度信息熵[23-26],形式如下:
| $ \overline {{S_n}} = \sum\limits_i {\left( {{\varepsilon _{{\text{a}},i}}{{\log }_2}{\varepsilon _{{\text{a}},i}} + {\varepsilon _{{\text{b}},i}}{{\log }_2}{\varepsilon _{{\text{b}},i}}} \right)} \frac{1}{{{S_0}}}\frac{{{N_{{\text{cell,}}i}}}}{{{N_{\text{p}}}}}, $ | (10) |
其中εa, i、εb, i分别表示在第i个三维网格内的a、b颗粒浓度,即a、b颗粒个数占该网格内颗粒数的比例,由
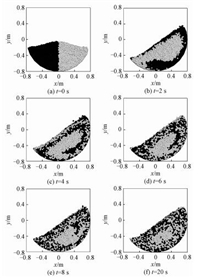
图 2显示转速为ω=1.0π rad/s不同时刻的颗粒混合情况。从图中可以看出,混合时颗粒分为流动表层和静态基底,在流动表层和静态基底之间有一个速度梯度较大的剪切层[27],因此存在强烈的剪切作用,所以黑白颗粒间的混合界面不断变形,之后随之出现复杂的细节并形成多离散的层次结构。混合界面随着时间的推移不断发展为愈加错综复杂的结构,混合界面的层次结构具有分形几何体的特性。这与之前的研究[2, 8]是相符的。回顾及参考圆形滚筒内颗粒混合过程及流态,颗粒混合流态一般随转速增加出现6种不同流态的过渡:滑移 (slipping),塌落 (slumping),滚动 (rolling),小瀑布 (cascading),大瀑布 (cataracting),离心 (centrifuging)[28]。
|
Download:
|
|
图 2 ω=1.0π (rad/s) 滚筒内颗粒随时间的演化 Fig. 2 Snapshots of particle motion in rotating tumbler at ω=1.0π rad/s |
|
一般而言,回转混合体不在过低及过高的转速,即滑移和离心流态下工作。其中,离心态是因为边界转速过高,颗粒之间由静摩擦产生的作用力已无法维持其整体与边界相同的转速旋转,因此,在颗粒与壁面之间将发生相对滑动。同时,颗粒分布紧贴壁面,形成环形颗粒分布形态。
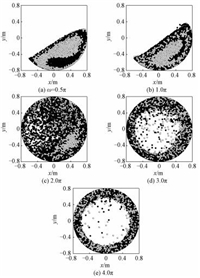
因此为讨论滚筒转速对颗粒混合的影响,图 3展示转速分别为0.5π,1.0π,2.0π,3.0π,4.0π rad/s旋转5 s时颗粒混合情况的比较。从图 3可以看出不同转速下呈现不同的混合状态。对比图 3(a)和图 3(b)可以发现,在转速不高,旋转时间相同时,转速更快的颗粒混合更加充分,这表明在转速不高的范围内,转速的提高可加速颗粒混合过程。继续对比图 3(c)、3(d)和3(e),当转速逐渐增加,颗粒流态逐渐由瀑布流态向离心态过渡。即便同为离心态,图 3(d)和3(e)中颗粒分布的环形也有所不同,速度更大的情况下,颗粒形成的“颗粒环”左右厚度更加均匀,从顶端落下的颗粒相对较少,此时已经无法从直观上定性分辨颗粒的混合程度,因此引入评估颗粒混合的函数。
|
Download:
|
|
图 3 不同转速旋转5 s颗粒混合情况 Fig. 3 Snapshots of particle mixing with different rotate speeds at moment t=5 s |
|
基于差值函数的物理性质,从图 4(a)~4(d)可以看出,随着时间的推移,不同转速下的差值函数xab、yab、uab和vab值越来越接近于0,在经过一段时间的混合后进入稳定阶段,最终稳定在0值附近震荡。速度越快,到达稳定阶段前所需的时间越短。这说明,随着滚筒的旋转,不同转速工况的混合程度逐渐增加,最终达到当前流态对应的极限发展状态。且到达极限发展状态的时间与速度呈负相关。而震荡的幅度与流态有关,当颗粒在滚动滑落的流态时,不同速度下的震荡幅值相近。而当颗粒运动进入离心态时,震荡幅度急剧增加,速度越大幅度越大,呈现明显的周期性特征。这个周期性与之前的研究相符合[8]。这是因为滚筒内颗粒混合是具有周期性的物理过程:静态基底内的颗粒沿壁面从右侧上升,经过上侧进入流动层,随流动层滑落至左下侧,再经由左下侧进入静态基底,如此往复循环。在没有达到离心态时,不同速度下的静态基底和流动表层之间距离区别不大,而当速度逐渐增大颗粒运动进入离心态时,颗粒紧贴壁面形成环状,流动表层的颗粒运动减少,静态基底和流动表层之间的距离也随之急剧减小,速度越大厚度越小,也因此导致了由滚筒旋转周期性变化引发的震荡幅度的急剧增加。而其值的震动幅度在稳定阶段之后衰减很小甚至不发生衰减,说明在高速离心态下颗粒之间基本不发生相对运动。与xab、yab、uab和vab不同,Rab和Uab评价的是所有颗粒的混合程度。但其也具有值越趋近于0,对应的混合情况越好的特性。

|
Download:
|
|
图 4 差值函数 Fig. 4 Difference value functions of particles |
|
如图 4(e)、4(f)所示,不同速度下的Rab和Uab皆随时间震荡递减,在速度没有达到离心态之前,Rab和Uab随时间的推移,最终递减至趋近于0,而当颗粒运动状态为离心态时,Rab和Uab随时间演化递减至一定值附近。而达到最终的稳定状态的时间和转速呈负相关,这与速度和位置差值的分析结果一致。这说明离心态时,其最终的混合情况是差于其他情况的。这是因为滚筒的旋转是逆时针方向,在滚筒初始旋转的时候,在左边的a颗粒不仅受到自身重力作用,还受到b颗粒的挤压阻碍运动,而与之相反的是b颗粒受到来自a颗粒的推动作用促进颗粒运动,因此在初始阶段,运动到相同位置的a,b颗粒的运动速度大小会有所区别。然而在没达到离心态时,随着时间的变化,颗粒混合逐渐演化,初始位置导致的差异逐渐减小以至于消失。但若滚筒速度过大以至于颗粒运动达到离心态,此时处于静态基底状态的颗粒增多,流动表层与静态基底的剪切作用削弱甚至消失,颗粒相对运动减缓甚至是停止的状态,此时因初始位置导致的差异无法再随着时间变化而减小,故趋近于一个较初始值小的定值。
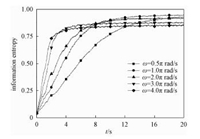
3.3 信息熵分析为了对比验证差值函数的正确性,我们还计算了基于局部浓度的信息熵。局部浓度信息熵能够量化三维空间上颗粒的混合程度,其值与混合程度成正比,其斜率即为混合的速率。由图 5可知,随着时间的推移,混合程度逐渐增加,并且最终达到稳定值,即极限发展状态,并且滚筒速度越快,信息熵的值稳定得越快,即达到极限发展状态所需的时间越短。这都与差值函数的分析相符。还可以观察到信息熵的斜率与滚筒速度大小正相关,这说明滚筒速度越快,初始混合的速率越快。当滚筒速度较大时 (ω=3.0π rad/s,ω=4.0π rad/s),其稳定时的信息熵小于滚筒速度较小时的信息熵,这表明颗粒未充分混合就进入离心态,验证了前文描述的进入离心态后颗粒之间几乎不再发生相对运动,所以其极限发展状态的混合情况差于非离心态的情况。从而验证差值函数可以评价颗粒混合情况。
|
Download:
|
|
图 5 基于局部浓度的信息熵 Fig. 5 Information entropy based on local concentration |
|
信息熵可以评价颗粒整体混合情况,但是计算较复杂,受到网格划分的影响较大[15]。与之相比较,差值函数的计算更为简单,不依赖于网格划分,而且可以判断不同方向上以及整体颗粒的混合情况。
4 总结本文使用DEM的软球模型对于三维旋转滚筒中颗粒的运动进行模拟,并提出新的评价函数,即差值函数。得出如下结论:
1) 滚筒内的颗粒混合是呈周期性变化的,并且颗粒混合过程存在着该工况下充分发展的极限。本文研究的工况中,在其他条件相同情况下,决定颗粒充分混合的极限状态最重要的因素是颗粒流态,颗粒流态取决于颗粒速度,而颗粒速度受到滚筒速度的影响。非离心流态下颗粒混合极限状态优于离心流态下的颗粒混合极限状态。在颗粒流态达到离心态之后,颗粒基本不发生混合,这说明离心态对颗粒混合起阻碍作用,在实际工业上,应尽量避免滚筒速度过大导致颗粒呈离心态流动。
2) 其次决定当前颗粒混合程度的因素为混合时间,其他条件相同时混合时间越长,颗粒混合程度越高;而且颗粒混合存在充分混合的极限状态,在达到该状态后,滚筒继续转动将失去意义。在工业应用中,在达到该状态后应停止滚筒以节省能源。
3) 与传统的评价颗粒混合程度的信息熵函数进行验证比较,验证了差值函数可以评价混合程度,并且具有计算更为简单、不依赖于网格划分、且可以判断不同方向以及整体颗粒混合情况的优点。
| [1] | Boateng A A. Rotary kilns:transport phenomena and transport processes[M]. Burlington: Butterworth-Heinemann, 2008. |
| [2] | 桂南.复杂两相流动中颗粒碰撞的DEM-LES/DNS耦合模拟研究[D].杭州:浙江大学, 2010. |
| [3] | Vargas W L, McCarthy J J. Heat conduction in granular materials[J]. AIChE Journal, 2001, 47(5):1052–1059. DOI:10.1002/(ISSN)1547-5905 |
| [4] | Arntz M, Den Otter W K, Briels W J, et al. Granular mixing and segregation in a horizontal rotating drum:a simulation study on the impact of rotational speed and fill level[J]. AIChE Journal, 2008, 54(12):3133–3146. DOI:10.1002/aic.v54:12 |
| [5] | 葛良, 桂南, 徐文凯, 等. 波形滚筒内颗粒混合和导热分布形态特性的研究[J]. 中国科学:技术科学, 2014(1):62–70. |
| [6] | Gui N, Fan J. Numerical study of heat conduction of granular particles in rotating wavy drums[J]. International Journal of Heat and Mass Transfer, 2015, 84:740–751. DOI:10.1016/j.ijheatmasstransfer.2015.01.064 |
| [7] | Gui N, Yang X, Tu J, et al. Numerical simulation and analysis of particle mixing and conduction in wavy drums[J]. Drying Technology, 2016, 34(1):91–104. DOI:10.1080/07373937.2015.1025140 |
| [8] | Gui N, Fan J R, Cen K F. A macroscopic and microscopic study of particle mixing in a rotating tumbler[J]. Chemical Engineering Science, 2010, 65(10):3034–3041. DOI:10.1016/j.ces.2010.01.023 |
| [9] | Yang S, Cahyadi A, Wang J, et al. DEM study of granular flow characteristics in the active and passive regions of a three-dimensional rotating drum[J]. AIChE Journal, 2016, 62(11):3874–3888. DOI:10.1002/aic.v62.11 |
| [10] | Wightman C, Moakher M, Muzzio F J, et al. Simulation of flow and mixing of particles in a rotating and rocking cylinder[J]. AIChE journal, 1998, 44(6):1266–1276. DOI:10.1002/aic.v44:6 |
| [11] | Sato Y, Nakamura H, Watano S. Numerical analysis of agitation torque and particle motion in a high shear mixer[J]. Powder Technology, 2008, 186(2):130–136. DOI:10.1016/j.powtec.2007.11.028 |
| [12] | Soni R K, Mohanty R, Mohanty S, et al. Numerical analysis of mixing of particles in drum mixers using DEM[J]. Advanced Powder Technology, 2016, 27(2):531–540. DOI:10.1016/j.apt.2016.01.016 |
| [13] | Siiriä S, Yliruusi J. Determining a value for mixing:mixing degree[J]. Powder Technology, 2009, 196(3):309–317. DOI:10.1016/j.powtec.2009.08.009 |
| [14] | Ayeni OO, Wu CL, Joshi JB, et al. A discrete element method study of granular segregation in non-circular rotating drums[J]. Powder Technology, 2015, 283:549–560. DOI:10.1016/j.powtec.2015.06.038 |
| [15] | Wen Y, Liu M, Liu B, et al. Comparative study on the characterization method of particle mixing index using DEM method[J]. Procedia Engineering, 2015, 102:1630–1642. DOI:10.1016/j.proeng.2015.01.299 |
| [16] | Ardekani A M, Rangel R H. Numerical investigation of particle-particle and particle-wall collisions in a viscous fluid[J]. Journal of fluid mechanics, 2008, 596:437–466. |
| [17] | Tsuji Y, Tanaka T, Ishida T. Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe[J]. Powder technology, 1992, 71(3):239–250. DOI:10.1016/0032-5910(92)88030-L |
| [18] | Mishra B K. A review of computer simulation of tumbling mills by the discrete element method:part Ⅰ-Contact mechanics[J]. International journal of mineral processing, 2003, 71(1):73–93. |
| [19] | Mishra BK. A review of computer simulation of tumbling mills by the discrete element method:Part Ⅱ-Practical applications[J]. International Journal of Mineral Processing, 2003, 71(1):95–112. |
| [20] | Weerasekara N S, Powell M S, Cleary P W, et al. The contribution of DEM to the science of comminution[J]. Powder technology, 2013, 248:3–24. DOI:10.1016/j.powtec.2013.05.032 |
| [21] | Shannon C E, Weaver W. The mathematical theory of communication[M]. Urbana, Illinois: University of Illinois Press, 1949. |
| [22] | Maione R, De Richter S K, Mauviel G, et al. DEM investigation of granular flow and binary mixture segregation in a rotating tumbler:influence of particle shape and internal baffles[J]. Powder Technology, 2015, 286:732–739. DOI:10.1016/j.powtec.2015.09.011 |
| [23] | Lai F S, Fan L T. Application of a discrete mixing model to the study of mixing of multicomponent solid particles[J]. Industrial & Engineering Chemistry Process Design and Development, 1975, 14(4):403–411. |
| [24] | Schutyser M A I, Weber F J, Briels W J, et al. Three-dimensional simulation of grain mixing in three different rotating drum designs for solid-state fermentation[J]. Biotechnology and Bioengineering, 2002, 79(3):284–294. DOI:10.1002/(ISSN)1097-0290 |
| [25] | Schutyser M A I, Padding J T, Weber F J, et al. Discrete particle simulations predicting mixing behavior of solid substrate particles in a rotating drum fermenter[J]. Biotechnology and bioengineering, 2001, 75(6):666–675. DOI:10.1002/(ISSN)1097-0290 |
| [26] | Masiuk S, Rakoczy R. The entropy criterion for the homogenisation process in a multi-ribbon blender[J]. Chemical Engineering and Processing:Process Intensification, 2006, 45(6):500–506. DOI:10.1016/j.cep.2005.11.008 |
| [27] | Metcalfe G, Shinbrot T, McCarthy JJ, et al. Avalanche mixing of granular solids[J]. 1995:39-41. |
| [28] | Mellmann J. The transverse motion of solids in rotating cylinders:forms of motion and transition behavior[J]. Powder Technology, 2001, 118(3):251–270. DOI:10.1016/S0032-5910(00)00402-2 |
 2017, Vol. 34
2017, Vol. 34 


