纤维过滤器由于其结构简单、制造成本低廉和过滤效率高的优点,常被用于分离流体中夹带的固相颗粒。在供暖、通风和空调系统 (HVAC)、火力发电、水泥制造、采矿工程等行业中有广泛应用。而在工业卫生领域,很多样品采集设备也常常用到纤维过滤器。对于纤维过滤器的发展过程,Davies[1]和Hinds[2]都曾详细介绍过。纤维过滤器捕集颗粒是一个复杂的颗粒-流体-纤维相互作用的非稳态过程,人们对捕集过程进行了大量的实验研究和数值模拟计算。早期研究人员的工作大多集中在圆形截面纤维。Kuwabara[3]最早利用斯托克斯近似等理论分析方法,研究黏性流体中随机分布和均匀分布的相互平行圆柱纤维所受曳力,得到气流垂直圆柱时纤维所受曳力的表达式;同年,Happel[4]利用同样的方法 (单元晶胞法) 得到流体速度平行及垂直圆柱时的半经验曳力公式。在这之后,Kuwabara或Happel流场就作为一种基础方法,在纤维捕集领域被许多研究人员所采用。基于该流场,Lee和Liu[5]通过边界层理论得到圆形截面纤维扩散和拦截机制下的捕集效率表达式。近几年,关于纤维捕集的研究又有了许多新的方法和进展。Qian等[6]利用CFD方法并结合离散元法 (DEM),模拟多纤维情况下的颗粒沉积情况以及不同工况下的过滤性能。Saleh等[7]分别采用3维微观模拟方法和1维宏观尺度模型模拟纤维过滤器的捕集性能,发现他们提出的1维宏观尺度模型可以较为准确并且快速地模拟捕集效率和系统压降。Soltani等[8]利用X射线方法得到真实的3维过滤器结构,并采用CFD技术模拟过滤器的捕集性能,发现不仅纤维体积分数会对过滤效率产生影响,纤维的放置角度也会影响颗粒的捕集。
目前,市场上销售的纤维过滤器大部分都是圆形截面纤维,随着制造技术以及测量技术的发展,也出现了椭圆形、矩形、楔形等截面形状的异形纤维过滤器[9]。由于异形纤维相对于圆形纤维有更大的比表面积,从而可能会具有更好的捕集效率。因此,非圆截面的纤维也开始进入研究人员的视野。不少学者已经使用理论分析或者数值模拟等方法对椭圆纤维捕集颗粒过程进行研究。Raynor[10]利用类似Kuwabara的方法研究椭圆纤维系统的压降,提出压降的计算公式。之后Regan和Raynor[11]又对椭圆纤维的扩散捕集效率进行研究,发现椭圆纤维的扩散捕集效率比圆柱纤维高,且和椭圆的长短轴之比成正比,而和椭圆纤维放置的方向关系不大。Raynor[12]还利用分析极限流线的方法研究椭圆纤维在拦截捕集机制下的捕集效率,提出椭圆纤维的拦截捕集效率公式。Wang和Pui[13]则主要考察椭圆纤维系统在不同捕集机制主导下的捕集效率,以及捕集效率与椭圆形状之间的关系。而对于矩形纤维,也已经有学者对其捕集颗粒过程进行了研究。Fardi和Liu[14-15]首先对错排矩形纤维的压降和捕集效率进行研究;Wang[16]研究包含多排矩形纤维的斯托克斯流场;Cheung等[17]对碰撞机制下的矩形纤维捕集效率进行研究;Adamiak[18]研究电场内正方形纤维对带电颗粒的捕集过程,主要考察带电颗粒的运动轨迹;Zhu等[19]研究惯性碰撞机制占主导时矩形和圆柱纤维的过滤过程。但是之前的工作缺少关于矩形纤维放置角度的变化对压降和捕集效率产生影响的研究,且对于矩形长宽比改变对捕集性能产生的影响也缺少定量的描述。
本文采用Wang等[20-21]提出的格子Boltzmann-元胞自动机概率 (LB-CA) 模型模拟矩形纤维捕集颗粒过程,该模型考虑了颗粒所受流体曳力及颗粒自身布朗力,通过对颗粒在规则格点上迁移的概率进行定量计算,能够准确地描述颗粒的运动细节。而对于流体,采用格子Boltzmann模型进行模拟,LB方法具有良好的并行性,计算简单,且能方便地考虑复杂边界条件,特别适合本文所考虑的矩形纤维的复杂边界形貌。采用该模型模拟得到扩散机制下矩形纤维周围流场压降和捕集效率,把模拟得到的值 (系统压降与捕集效率) 与相同体积分数圆形纤维理论值相比,得到对应修正系数。用Levenberg-Marquardt (L-M) 方法[22]对计算得到的修正系数进行处理,拟合出符合变化规律和精度要求的公式。
1 模型介绍 1.1 标准格子Boltzmann模型格子Boltzmann方法中,把流体抽象为微观的虚拟颗粒。如今最为广泛应用的LB模型是LBGK模型[23]。该模型的粒子分布函数演化方程如下:
| $ \begin{array}{*{20}{c}} {{f_i}\left( {\mathit{\boldsymbol{x + }}{\mathit{\boldsymbol{c}}_i}\Delta t,t + \Delta t} \right) - {f_i}\left( {\mathit{\boldsymbol{x}},t} \right)} \\ { = - \frac{1}{\tau }\left[ {{f_i}\left( {\mathit{\boldsymbol{x}},t} \right) - f_i^{eq}\left( {\mathit{\boldsymbol{x}},t} \right)} \right],} \end{array} $ | (1) |
其中:fi(x, t)是t时刻x处速度为ci的虚拟流体颗粒的概率密度,τ是与黏性及扩散率有关的无量纲松弛时间,
Qian等提出的DnQb模型[24](n代表空间维度,b代表离散速度) 是最为经典的LBGK模型。在该模型中,离散速度的计算如下:
| $ {\mathit{\boldsymbol{c}}_i} = \left\{ \begin{gathered} \left( {0,0} \right),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 0, \hfill \\ c\left( {\cos \left( {i - 1} \right)\frac{{\rm{ \mathsf{ π} }}}{2},\sin \left( {i - 1} \right)\frac{{\rm{ \mathsf{ π} }}}{2}} \right),\;\;\;\;\;\;\;\;\;\;\;\;i = 1,2,3,4, \hfill \\ \sqrt 2 c\left( {\cos \left( {2i - 9} \right)\frac{{\rm{ \mathsf{ π} }}}{4},\sin \left( {2i - 9} \right)\frac{{\rm{ \mathsf{ π} }}}{4}} \right),\;\;\;i = 5,6,7,8. \hfill \\ \end{gathered} \right. $ | (2) |
其中:c=Δx/Δt是虚拟颗粒的离散速度,Δx格子长度,Δt是时间步长。DnQb模型中应用最多的是D2Q9模型,此时平衡态分布函数如下:
| $ f_i^{{\rm{eq}}} = \mathit{\boldsymbol{\rho }}{\mathit{\boldsymbol{\omega }}_i}\left( {1 + \frac{{{\mathit{\boldsymbol{c}}_i} \cdot \mathit{\boldsymbol{u}}}}{{c_s^2}} + \frac{{{{\left( {{\mathit{\boldsymbol{c}}_i} \cdot \mathit{\boldsymbol{u}}} \right)}^2}}}{{2c_s^4}} - \frac{{{\mathit{\boldsymbol{u}}^2}}}{{2c_s^2}}} \right). $ | (3) |
初始时刻
| $ {\mathit{\boldsymbol{\omega }}_i} = \left\{ \begin{gathered} \frac{4}{9},\;\;\;i = 0, \hfill \\ \frac{1}{9},\;\;\;i = 1,2,3,4, \hfill \\ \frac{1}{{36}},\;\;i = 5,6,7,8. \hfill \\ \end{gathered} \right. $ | (4) |
流体的密度和动量的计算如下:
| $ \begin{gathered} \rho \left( {\mathit{\boldsymbol{x}},t} \right) = \sum\limits_i {{f_i}\left( {\mathit{\boldsymbol{x}},t} \right)} , \hfill \\ \rho \mathit{\boldsymbol{u}}\left( {\mathit{\boldsymbol{x}},t} \right) = \sum\limits_i {{\mathit{\boldsymbol{c}}_i}{f_i}\left( {\mathit{\boldsymbol{x}},t} \right)} . \hfill \\ \end{gathered} $ | (5) |
流体黏度和压力计算公式为
| $ \left\{ \begin{gathered} v = \frac{{c_s^2}}{2}\left( {2\tau - 1} \right)\Delta t, \hfill \\ P = \rho c_s^2. \hfill \\ \end{gathered} \right. $ | (6) |
对于颗粒运动,本文采用Wang等[20-21]建立的格子Boltzmann-元胞自动机概率 (LB-CA) 模型。由于本文研究的是布朗机制主导下的捕集效率,因此只考虑流体曳力以及随机布朗力[25]对颗粒的作用。因此单位质量颗粒的受力方程如下
| $ \frac{{{\rm{d}}{\mathit{\boldsymbol{u}}_{\rm{p}}}}}{{{\rm{d}}t}} = {\mathit{\boldsymbol{F}}_{\rm{D}}} + {\mathit{\boldsymbol{F}}_{\rm{B}}} = \frac{{\mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{u}}_{\rm{p}}}}}{{{\tau _{\rm{p}}}}} + \zeta \sqrt {\frac{{216\mu {k_{\rm{B}}}T}}{{{\rm{ \mathsf{ π} }}\rho _{\rm{p}}^2d_{\rm{p}}^5\Delta t}}} , $ | (7) |
其中:up为颗粒速度;τp为颗粒弛豫时间尺度,τp=ρpdp2/(18μ),μ为气体动力黏度;FB为随机布朗力;ζ为平均值0、方差为1的高斯随机数;dp为颗粒直径;kB为Boltzmann常数;T为温度。
通过对方程 (7) 进行2次积分, 可以依次得到颗粒的速度和位移2个公式:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{u}}_{\rm{p}}^{n + 1} = \mathit{\boldsymbol{u}}_{\rm{p}}^n\exp \left( { - \frac{{\Delta t}}{{{\tau _{\rm{p}}}}}} \right) + \left( {\mathit{\boldsymbol{u}} + {\mathit{\boldsymbol{F}}_{\rm{B}}}{\tau _{\rm{p}}}} \right)} \\ {\left( {1 - \exp \left( { - \frac{{\Delta t}}{{{\tau _{\rm{p}}}}}} \right)} \right),} \end{array} $ | (8) |
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}_{\rm{p}}^{n + 1} = \mathit{\boldsymbol{x}}_{\rm{p}}^n + \left( {\mathit{\boldsymbol{u}}_{\rm{p}}^n - \mathit{\boldsymbol{u}}} \right)\left( {1 - \exp \left( { - \frac{{\Delta t}}{{{\tau _{\rm{p}}}}}} \right)} \right){\tau _{\rm{p}}} + \mathit{\boldsymbol{u}}\Delta t + } \\ {\left( {\Delta t - \left( {1 - \exp \left( { - \frac{{\Delta t}}{{{\tau _{\rm{p}}}}}} \right)} \right){\tau _{\rm{p}}}} \right){\mathit{\boldsymbol{F}}_{\rm{B}}}{\tau _{\rm{p}}}.} \end{array} $ | (9) |
上标n表示当前时刻,n+1表示下一时刻。
由上述公式可得到颗粒在Δt内的实际位移
| $ {p_i} = \max \left( {0,\frac{{d\mathit{\boldsymbol{x}} \cdot {\mathit{\boldsymbol{e}}_i}}}{{\Delta x}}} \right),\left( {i = 1,3,5,7} \right), $ | (10) |
其中Δx为格子长度。最终可以确定颗粒的最终格点位置:
| $ \mathit{\boldsymbol{x}}_{\rm{p}}^{n + 1} = \mathit{\boldsymbol{x}}_{\rm{p}}^n + {\mu _1}{\mathit{\boldsymbol{e}}_1} + {\mu _3}{\mathit{\boldsymbol{e}}_3} + {\mu _5}{\mathit{\boldsymbol{e}}_5} + {\mu _7}{\mathit{\boldsymbol{e}}_7}. $ | (11) |
其中μi为一个布尔量,取1的概率为pi。
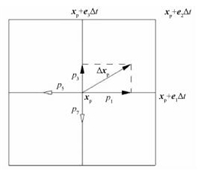
以图 1为例,p1>0, p3>0, p5=0, p7=0(因为ei=-ei+4,pi×pi+4=0)。此时通过2个均匀分布于[0,1]区间的随机数r1和r2,可确定颗粒最终位置如下:
|
Download:
|
|
图 1 颗粒运动规则 Fig. 1 Particle transport rule in the CA probabilistic model |
|
| $ \left\{ \begin{gathered} 如果{r_1} > {p_1},{r_2} > {p_3},\mathit{\boldsymbol{x}}_{\rm{p}}^ * = {\mathit{\boldsymbol{x}}_{\rm{p}}}, \hfill \\ 如果{r_1} < {p_1},{r_2} > {p_3},\mathit{\boldsymbol{x}}_{\rm{p}}^ * = {\mathit{\boldsymbol{x}}_{\rm{p}}} + {\mathit{\boldsymbol{e}}_1}\Delta t, \hfill \\ 如果{r_1} > {p_1},{r_2} < {p_3},\mathit{\boldsymbol{x}}_{\rm{p}}^ * = {\mathit{\boldsymbol{x}}_{\rm{p}}} + {\mathit{\boldsymbol{e}}_3}\Delta t, \hfill \\ 如果{r_1} < {p_1},{r_2} < {p_3},\mathit{\boldsymbol{x}}_{\rm{p}}^ * = {\mathit{\boldsymbol{x}}_{\rm{p}}} + {\mathit{\boldsymbol{e}}_2}\Delta t. \hfill \\ \end{gathered} \right. $ | (12) |
作用在单位长度纤维上的无量纲曳力常常用来表征纤维过滤器的压降。Kuwabara[3]通过求解极坐标下的流函数方程得到圆柱纤维的无量纲曳力表达式:
| $ {F_{\text{O}}} = 4{\text{π}}{\left[ { - 0.5\ln \alpha - 0.75 - 0.25{\alpha ^2} + \alpha } \right]^{ - 1}}, $ | (13) |
由式 (13) 可知,对于圆形纤维来说,纤维所受的无量纲曳力只与纤维的体积分数 (α) 有关。但是在本文中,考虑的是矩形纤维的压降,所以情况更为复杂,单单一个体积分数无法表明矩形纤维的压降变化规律。我们还要考虑不同的长宽比 (ε) 以及不同的放置角度 (θ) 对纤维所受曳力的影响。把通过模拟计算得到的矩形纤维曳力与相同体积分数的圆形纤维理论曳力值相比,得到相应的比例系数:CR, F=FR/FO。FR代表矩形纤维所受无量纲曳力,FO表示相同体积分数圆形纤维所受曳力。通过改变体积分数、长宽比或放置角度,得到不同工况下的矩形纤维曳力,从而得到一系列的比例系数。
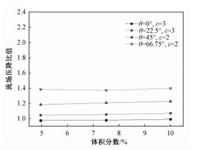
首先分析体积分数对矩形纤维周围流场压降的影响。从图 2中可以发现,当放置角度和长宽比一定时,矩形纤维压降比值与体积分数 (5%~10%) 几乎无关。最大的体积分数取10%是因为,当体积分数太大时,会导致矩形纤维偏大,超出计算区域的边界。
|
Download:
|
|
图 2 矩形纤维压降比值与体积分数关系 Fig. 2 Pressure drop ratio vs. volume fraction |
|
除上述分析的因素以外,可能对纤维压降产生影响的因素是流体速度以及流体运动黏度。以前研究大多认为在雷诺数Re(=Udf/v) 小于1时,圆形纤维的无量纲曳力几乎不随雷诺数变化[26]。为了验证矩形纤维是否满足这一规律,本文以矩形纤维在长宽比2,放置角度45°下的工况为例,分别改变入口速度和动力黏度这2个参数来改变Re,模拟结果如表 1所示。从表中结果可以发现,该工况下矩形纤维受到无量纲曳力随Re变化非常小。该结论与Fardi和Liu[15]得出的矩形纤维压降随Re变化规律保持一致。本文模拟的所有工况均满足Re < 1。
|
|
表 1 流场性质对于压降的影响 Table 1 Influence of fluid properties on the dimensionless force on a rectangular fiber |
当计算得到一系列矩形压降的比例系数后,可以用L-M方法拟合出最符合其变化规律的函数:CR, F=f(ε, θ, α)。根据上述分析,纤维体积分数与压降比例系数无关,所以拟合公式可以简化为CR, F=f(ε, θ)。
图 3为用格子Boltzmann方法模拟的矩形纤维随不同放置角度θ的流场变化示意图。从图中可以看出角度的变化对流场的影响比较大。角度越大,纤维周围流场的扰动越大。分析矩形纤维的对称性可知,只需要研究0到π/2的情况就可以得到任一角度的系统压降。本文考虑5种长宽比的矩形,即ε=2~6的矩形。每种长宽比模拟5个放置角度的压降,即θ=0,θ=π/8,θ=π/4,θ=3π/8,θ=π/2。

|
Download:
|
|
图 3 矩形纤维 (ε=3) 流场 Fig. 3 Flow fields around rectangular fibers |
|
在相同的体积分数下,矩形纤维的压降与它的长宽比以及放置角度有关 (如图 4所示)。从图 4可以看到不同长宽比以及不同放置角度下的矩形纤维的系统压降变化情况。从图中还可以发现,当θ=0°时,随着长宽比ε增大 (对于矩形纤维来说,ε越大纤维就越细长),系统压降先减小后增大。这是因为在θ=0°且长宽比较小时,迎风面积对曳力的影响比摩擦面积对曳力影响要大,随着长宽比增大,迎风面积减小,所以系统的压降也减小;但是当长宽比增大到一定程度时,迎风面积对系统压降的影响力小于摩擦面积的影响能力,因而随着ε增大到大于4时,系统压降随着ε增大而增大。在θ=22.5°,45°,67.5°,90°时,系统压降随着长宽比ε增大而增大。从图 4中可以看出,在特定的长宽比ε下,系统压降随着放置角度的增大而增大,且增大的趋势很明显。且当ε越大,系统压降随角度增大而增大的趋势就越明显。这是由于迎风面积直接由θ决定,在摩擦面积一定的情况下,θ越大,迎风面积越大,系统压降越大。

|
Download:
|
|
图 4 矩形纤维与同体积圆形纤维压降之比ΔPR/ΔPO vs. ε(a) 和ΔPR/ΔPO vs. sinθ (b) Fig. 4 Pressure drop ratio vs. ε (a) and vs. sinθ (b) |
|
从图 4中还可以看出,当放置角度θ保持不变时,矩形纤维的压降比与长宽比ε呈二次方关系,所以修正系数可以表示为CR, F=γ1×ε2+γ2×ε+γ3;当长宽比ε保持不变时,矩形纤维的压降比与角度θ的sin值呈指数关系,所以修正系数可以表示为CR, F=δ1×exp (-sinθ/δ2)+δ3。可以清楚地看出修正系数与θ和ε相关,把这2个影响因素统一到同一个式子中即可得到所需的修正公式。本文假设公式为:CR, F=η1×exp (-sinθ/η2)+η3,而其中的η1,η2,η3都可以采用关于ε的二次式来表示,即
| $ \begin{gathered} {C_{{\rm{R,F}}}} = \left( {{\beta _1} \times {\varepsilon ^2} + {\beta _2} \times \varepsilon + {\beta _3}} \right) \times \hfill \\ \;\;\;\;\;\;\;\;\;\;\exp \left( { - \sin \theta /\left( {{\beta _4} \times {\varepsilon ^2} + {\beta _5} \times \varepsilon } \right.} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\left. {\left. { + {\beta _6}} \right)} \right) + {\beta _7} \times {\varepsilon ^2} + {\beta _8} \times \varepsilon + {\beta _9}. \hfill \\ \end{gathered} $ | (14) |
然后将模拟得到的各个工况下的压降修正系数作为样本,采用L-M方法得到未知系数的最佳估计值,如下:
| $ \begin{gathered} {\beta _1} = - 0.004\;751\;3,{\beta _2} = 0.037\;043\;9,{\beta _3} = \hfill \\ - 0.033\;257\;1,{\beta _4} = 0.005\;455\;9,{\beta _5} = - 0.014\;001\;5, \hfill \\ {\beta _6}{\text{ = }} - 0.318\;247\;4,{\beta _7} = 0.015\;960\;3,{\beta _8} = - 0.112\;366\;3, \hfill \\ {\beta _9} = 1.136\;794\;7。 \hfill \\ \end{gathered} $ |
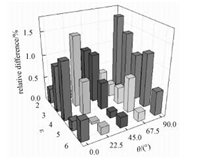
得到公式 (14) 之后,对于矩形纤维,给定任意的角度θ和长宽比ε,都可以求出对应的修正系数CR, F,再根据式 (13),就可以求得该工况下矩形纤维流场的系统压降。验证拟合公式计算发现,如图 5所示,式 (14) 的计算所得结果与程序模拟得到的结果拟合很好,最大误差不超过1.63%。证明式 (14) 不仅简洁,而且能较准确地计算不同放置角度θ与长宽比ε下矩形纤维流场的系统压降。
|
Download:
|
|
图 5 模拟值与拟合公式计算值的对应误差 Fig. 5 Relative differences between CE, F and simulation results |
|
相比于圆形纤维,矩形纤维有更大的比表面积,对细颗粒捕集更有效果。由于细小颗粒主要由扩散机制主导,因此本文主要研究扩散捕集效率。并且相比于拦截与惯性碰撞这两种机制,扩散机制下的理论公式更成熟,也被人们更为广泛地认同。因此在圆形纤维扩散捕集效率理论公式的基础上,采用与矩形纤维压降拟合公式类似的处理方法,即引入一个矩形纤维扩散捕集效率与同体积分数圆形纤维扩散捕集效率理论值的比值CR, D:CR, D=ηR, D/ηO, D,作为修正系数,再用L-M方法求得修正系数满足的公式,就可以得到有较高精确度的矩形纤维扩散捕集效率拟合公式。其中ηR, D为矩形纤维扩散捕集效率,ηO, D为相同体积分数圆形纤维扩散捕集效率,下标D表示扩散捕集机制。本文所用的作为基准的圆形扩散机制的理论公式采用Stechkina和Fuchs[27]提出的公式:
| $ \begin{gathered} {\eta _{{\rm{O}},{\rm{D}}}} = 2.9K{u^{ - 1/3}}P{e^{ - 2/3}} + 0.62P{e^{ - 1}}, \hfill \\ Ku = - 0.5\ln \alpha - 0.75 + \alpha - 0.25{\alpha ^2}. \hfill \\ \end{gathered} $ | (15) |
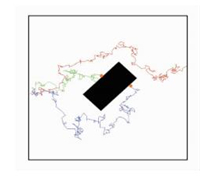
当布朗扩散机制占主导时,颗粒的捕集效率与贝克莱数Pe相关,Pe=Udf/D,D即为布朗扩散系数,D的表达式为D=KBT/(3πμdp),其中U为来流速度,df为纤维的直径。扩散机制产生的原因最主要是因为受到布朗力的作用。布朗力是由颗粒周围流场的流体分子撞击产生的,分子撞击的不规则性导致布朗力的不规则性,布朗力的不规则性导致扩散机制下颗粒运动的不规则性。颗粒越小,布朗力的随机性越明显,扩散机制越强。颗粒在矩形纤维周围流场中的扩散运动如图 6所示。
|
Download:
|
|
图 6 扩散机制下的颗粒运动轨迹图 Fig. 6 Particle trajectories in diffusion mechanism |
|
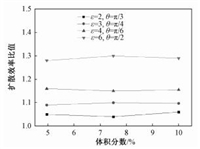
同样先研究不同体积分数对矩形纤维扩散捕集效率的影响。从图 7中可以发现,矩形纤维扩散效率比值随体积分数变化很小,为简化分析,同样可以认为与体积分数无关。因此接下来也主要讨论放置角度以及长宽比对扩散效率的影响。
|
Download:
|
|
图 7 扩散效率比值与体积分数关系 Fig. 7 Diffusional collection efficiency ratio vs. α |
|
广泛认为,扩散机制下,颗粒捕集效率与放置角度无关。我们的模拟结果也证明了这一点。表 2为Pe=235时,不同放置角度θ下的矩形纤维的扩散捕集效率。由表中的数据可以发现,随着放置角度θ的增大,扩散捕集效率基本保持不变。事实上,由于布朗扩散较强,颗粒可能沉积在纤维表面的任一位置。所以当长宽比ε相同时,不同的放置角度θ有相同的捕集面积,这就导致扩散捕集效率与放置角度θ基本无关。
|
|
表 2 矩形纤维与相同体积分数圆形在不同角度下的扩散捕集效率比值 (Pe=235) Table 2 Diffusional collection efficiency ratio of rectangular to circular fibers (Pe=235) |
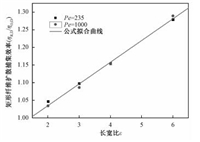
图 8为不同的Pe数时,矩形扩散捕集效率比值与ε的关系。从式 (15) 可知,圆形纤维的扩散效率的值与Pe数有关。但从图 8可以看出,扩散捕集效率比值CR, D与Pe数无关。这可能是因为在圆的理论扩散捕集效率中已经充分考虑了Pe数的影响。从图 8还可以看出扩散效率比值随ε增大而增大。这是因为当长宽比ε增大时,矩形纤维的捕集面积增大,从而增大了扩散捕集效率。并且扩散捕集效率的比值大致与长宽比ε呈线性关系。所以修正系数的拟合公式为
|
Download:
|
|
图 8 矩形纤维扩散效率比值随ε变化关系 Fig. 8 Diffusional collection efficiency ratio vs. ε |
|
| $ {C_{{\text{R}},{\text{D}}}} = {\beta _1} \times \varepsilon + {\beta _2}, $ | (16) |
通过L-M方法得到的各个未知参数最佳估计值,如下:β1=0.061 605 563 3,β2=0.912 105 734。
根据得到的拟合公式 (16),再结合原有的圆形纤维扩撒捕集效率的理论公式 (15),可以方便地求出矩形纤维在任意长宽比和放置角度下的扩散效率。如表 3所示,由拟合公式 (15) 计算得到的矩形扩散效率误差不超过1.117%。
|
|
表 3 矩形纤维拟合公式误差分析表 Table 3 Relative differences between CR, D and simulation results |
本文采用格子Boltzmann元胞自动机概率 (LB-CA) 模型,能够有效地对矩形纤维周围流场压降和扩散机制下捕集效率进行模拟。通过计算与分析得到以下结论:矩形纤维周围流场压降与同体积分数圆形纤维压降的比值 (CR, F) 与纤维体积分数无关;当雷诺数小于1时,矩形纤维所受的无量纲曳力基本不随雷诺数的改变而改变;通过分析CR, F随放置角度及长宽比的变化规律得到相应的拟合公式CR, F=(β1×ε2+β2×ε+β3)×exp (-sinθ/(β4×ε2+β5×ε+β6))+ β7×ε2+β8×ε+β9,所求公式的预测误差小于1.63%。矩形纤维与圆形纤维扩散效率的比值同样不随体积分数改变而改变;放置角度对于矩形扩散效率的影响基本可以忽略;矩形纤维扩散效率比值与长宽比成正比,而与Pe数无关,对应的拟合公式为CR, D=β1×ε+β2,该公式的预测误差小于1.12%。利用求得的矩形纤维压降和扩散效率拟合公式,再结合圆形纤维对应理论公式,就可以计算不同工况下的矩形纤维流场压降和扩散捕集效率。
| [1] | Davies C N. Air filtration[M]. London: Academic Press, 1973. |
| [2] | Hinds W C. Aerosol technology:properties, behavior, and measurement of airborne particles[M]. New York: Wiley-Interscience, 1982. |
| [3] | Kuwabara S. The forces experienced by randomly distributed parallel circular cylinders or spheres in a viscous flow at small Reynolds numbers[J]. Journal of the Physical Society of Japan, 1959, 14(4):527–532. DOI:10.1143/JPSJ.14.527 |
| [4] | Happel J. Viscous flow relative to arrays of cylinders[J]. AIChE Journal, 1959, 5(2):174–177. DOI:10.1002/(ISSN)1547-5905 |
| [5] | Lee K W, Liu B Y H. Theoretical study of aerosol filtration by fibrous filters[J]. Aerosol Science and Technology, 1982, 1(2):147–161. DOI:10.1080/02786828208958584 |
| [6] | Qian F, Huang N, Zhu X, et al. Numerical study of the gas-solid flow characteristic of fibrous media based on SEM using CFD-DEM[J]. Powder Technology, 2013, 249(11):63–70. |
| [7] | Saleh A M, Hosseini S A, Tafreshi H V, et al. 3-D microscale simulation of dust-loading in thin flat-sheet filters:a comparison with 1-D macroscale simulations[J]. Chemical Engineering Science, 2013, 99(32):284–291. |
| [8] | Soltani P, Johari M S, Zarrebini M. Effect of 3D fiber orientation on permeability of realistic fibrous porous networks[J]. Powder Technology, 2014, 254(c):44–56. |
| [9] | Hutten I M. Handbook of nonwoven filter media[M]. Amsterdam: Elsevier, 2007. |
| [10] | Raynor P C. Flow field and drag for elliptical filter fibers[J]. Aerosol Science and Technology, 2002, 36(12):1118–1127. DOI:10.1080/02786820290092159 |
| [11] | Regan B D, Raynor P C. Single-fiber diffusion efficiency for elliptical fibers[J]. Aerosol Science and Technology, 2009, 43(6):533–543. DOI:10.1080/02786820902777215 |
| [12] | Raynor P C. Single-fiber interception efficiency for elliptical fibers[J]. Aerosol Science and Technology, 2008, 42(6):357–368. |
| [13] | Wang J, Pui D Y H. Filtration of aerosol particles by elliptical fibers:a numerical study[J]. Journal of Nanoparticle Research, 2009, 11(1):185–196. DOI:10.1007/s11051-008-9422-z |
| [14] | Fardi B, Liu B Y H. Flow field and pressure drop of filters with rectangular fibers[J]. Aerosol Science and Technology, 1992, 17(1):36–44. DOI:10.1080/02786829208959558 |
| [15] | Fardi B, Liu B Y H. Efficiency of fibrous filters with rectangular fibers[J]. Aerosol Science and Technology, 1992, 17(1):45–58. DOI:10.1080/02786829208959559 |
| [16] | Wang C. Stokes flow through an array of rectangular fibers[J]. International Journal of Multiphase Flow, 1996, 22(1):185–194. DOI:10.1016/0301-9322(95)00063-1 |
| [17] | Cheung C S, Cao Y H, Yan Z D. Numerical model for particle deposition and loading in electret filter with rectangular split-type fibers[J]. Computational Mechanics, 2005, 35(6):449–458. DOI:10.1007/s00466-004-0634-5 |
| [18] | Adamiak K. Viscous flow model for charged particle trajectories around a single square fiber in an electric field[J]. Industry Applications, IEEE Transactions on, 1999, 35(2):352–358. DOI:10.1109/28.753628 |
| [19] | Zhu C, Lin C H, Cheung C S. Inertial impaction dominated fibrous filtration with rectangular or cylindrical fibers[J]. Powder technology, 2000, 112(1):149–162. |
| [20] | Wang H, Zhao H, Guo Z, et al. Numerical simulation of particle capture process of fibrous filters using Lattice Boltzmann two-phase flow model[J]. Powder Technology, 2012, 227(9):111–122. |
| [21] | Wang H, Zhao H, Wang K, et al. Simulating and modeling particulate removal processes by elliptical fibers[J]. Aerosol Science and Technology, 2014, 48(2):207–218. DOI:10.1080/02786826.2013.868595 |
| [22] | More J. The Levenberg-Marquardt algorithm:implementation and theory[J]. Numerical analysis. Springer Berlin Heidelberg, 1978:105–116. |
| [23] | Chen S, Doolen G D. Lattice Boltzmann method for fluid flows[J]. Annual Review of Fluid Mechanics, 1998, 30(1):329–364. DOI:10.1146/annurev.fluid.30.1.329 |
| [24] | Qian Y H, D'Humieres D, Lallemand P. Lattice BGK models for Navier-Stokes equation[J]. EPL (Euro physics Letters), 1992, 17(6):479–484. DOI:10.1209/0295-5075/17/6/001 |
| [25] | Hosseini S A, Tafreshi H V. Modeling particle filtration in disordered 2-D domains:a comparison with cell models[J]. Separation and Purification Technology, 2010, 74(2):160–169. DOI:10.1016/j.seppur.2010.06.001 |
| [26] | Liu Z G, Wang P K. Pressure drop and interception efficiency of multifiber filters[J]. Aerosol Science and Technology, 1997, 26(4):313–325. DOI:10.1080/02786829708965433 |
| [27] | Stechkina I B, Fuchs N A. Fuchs N A. Studies on fibrous aerosol filters-I. Calculation of diffusional deposition of aerosols in fibrous filters[J]. Annals of Occupational Hygiene, 1966, 9(2):59–64. |
 2017, Vol. 34
2017, Vol. 34 


