2. Petroleum Engineering Department of Colorado School of Mines, Golden 80401
2. Petroleum Engineering Department of Colorado School of Mines, Golden 80401, USA
流体-颗粒流化系统在不同密度比下表现出大量复杂的非均匀流动结构,范围涵盖从一维结构的推进波到气泡形式的空隙[1]。非均匀流动结构的产生改变了系统中流体和颗粒两相相互作用,进而影响系统的流体动力学特性。现有的流体颗粒两相流动研究侧重于对均匀流动和非均匀流动结构下流体-颗粒相间曳力的研究[2-6],而对于系统从稳定状态到不稳定状态的转变研究不多[7-8],缺少描述流动不稳定性的方法和特征参数。传统的双流体模型和离散颗粒模型能够得到介观和宏观上流化系统内物理量的变化关系,但是限于计算方法和计算模型,尚不能获得微观上两相流动的特性参数。格子-Boltzmann模拟方法是近年发展起来的一种典型的、能够模拟复杂流动现象的数值计算方法[9]。格子-Boltzmann方法的主要思想是从微观的角度出发,以简单规则的粒子运动描述复杂多变的宏观流动现象,进而获得两相流动过程中流体和颗粒详尽的流动信息。本文采用格子-Boltzmann方法,详细研究特定颗粒雷诺数下,密度变化范围较大时两相流动的不稳定性。结合结构因子分析,确定随密度比增大时,颗粒-流体流动由稳定转变为不稳定的过程中颗粒速度特性变化规律及其与聚团形成的关系,进一步确定流体-颗粒两相不稳定流动产生时所对应的密度比范围。
1 计算模型本文采用格子-Boltzmann模拟方法进行研究,模拟采用Ladd[10]开发的用于计算球形颗粒的SUSP-3D程序,颗粒碰撞采用硬球模型。该方法的详细介绍和讨论可参见Ladd和Verberg[11]的研究。不同于直接求解运动的连续性方程,格子-Boltzmann方法通过将流体分子转化为具有离散速度的充满空间的格子来模拟流体分子的速度分布方程。诸如质量、动量和应力可以通过速度分布方程的矩来获得。对于分布方程的修正要使得宏观量在大的时间和空间尺度上遵循Navier-Stokes方程。本文采用的格子-Boltzmann方法的速度分布方程利用D3Q19模型,即三维空间中连续分布的流体分子速度被离散为19个离散速度。速度分布的更新采用两步完成:碰撞和迁移。在碰撞步,每个格子点上拥有不同速度的分子群体的重新布置遵循质量和动量守恒,从而使速度分布方程松弛到一个平衡状态。在迁移步,流体分子基于碰撞后的分布特性而移动到相邻的格子点上。这种方法通过与马赫数平方成比例的不可压缩误差重新获得了平均速度和压力场与不可压缩Navier-Stokes方程在小马赫数时的关系。马赫数被定义为流体动力学速度与绝热状态下声速之比。采用格子间距和时间步长无量纲化后的绝热声速为
颗粒运动通过求解每一个球形颗粒的线性和角动量守恒方程获得。方程中颗粒的受力采用颗粒所受到的流体作用力和转矩来确定。流体作用力和转矩通过积分求解由格子-Boltzmann方法模拟和润滑修正后的应力分布来确定。
2 计算方法和条件采用一维系统的流化过程进行模拟研究,对于每一个颗粒-流体的密度比,计算5个颗粒位置随机分布的两相流动系统。模拟颗粒采用球形颗粒,边界采用周期性边界条件。具体计算参数见表 1。
|
|
表 1 计算参数 Table 1 Simulation parameters |
模拟在一个三维的计算域中进行。初始时刻,1 239个无重叠的球形颗粒均匀随机分布在计算域中,产生的颗粒浓度为
| $ \phi {\text{ = }}\frac{{N{\text{π}}d_{\text{p}}^3}}{{6V}}, $ | (1) |
通过施加重力,每个颗粒将受到一个由于重力和浮力共同作用的力
| $ \mathit{\boldsymbol{F = }}\frac{{{\rm{ \mathsf{ π} }}d_{\rm{p}}^3}}{6}\left( {{\rho _{\rm{p}}} - {\rho _{\rm{f}}}} \right)g. $ | (2) |
压力梯度同样应用于流体以保证系统的净体积流量为零。在模拟的初始时刻,流体和颗粒静止不动,在y方向上施加重力后,颗粒开始流动,模拟结果采用系统颗粒平均速度达到稳定状态后的数据。
由于颗粒终端速度不是模拟的输入参数,能够准确控制系统流化的无量纲数为Archimedes数,定义如下
| $ Ar = \frac{{{\rho _{\text{f}}}\left( {{\rho _{\text{p}}} - {\rho _{\text{f}}}} \right)gd_{\text{p}}^3}}{{{\eta ^2}}}. $ | (3) |
颗粒的终端Reynolds数为Ret=ρfutdp/η。对于给定的流体颗粒流化系统 (ρp,ρf,dp,η),颗粒终端Reynolds数和Archimedes数之间存在如下关系[12]
| $ Ar = \left\{ \begin{gathered} 18R{e_{\text{t}}}\left[ {1 + 0.131\;5R{e_{\text{t}}}^{\left( {0.82 - 0.05{\text{lo}}{{\text{g}}_{10}}R{e_{\text{t}}}} \right)}} \right],0.01{\text{ < }}R{e_{\text{t}}} < 20, \hfill \\ 18R{e_{\text{t}}}\left[ {1 + 0.193\;5R{e_{\text{t}}}^{0.6305}} \right],\;\;\;\;\;\;\;\;\;\;\;\;20 < R{e_{\text{t}}} < 260. \hfill \\ \end{gathered} \right. $ | (4) |
在本文中,采用的Archimedes数对应于颗粒终端Reynolds数为30。
本文通过计算如下参数确定流体-颗粒两相流动系统不稳定流动状态产生时对应的密度比。
1) 平均流化速度,即当颗粒流化达到稳定状态后,所有颗粒的平均速度
| $ \bar u = \frac{1}{n}\sum\limits_{i = 1}^N {{u_i}} . $ | (5) |
2) 方差,统计获得颗粒速度的方差
| $ \operatorname{var} \left( u \right) = E\left[ {{{\left( {{u_i} - \bar u} \right)}^2}} \right]. $ | (6) |
3) 偏度,即三阶标准化矩
| $ {\text{skew}}\left( u \right) = E\left[ {{{\left( {\frac{{{u_i} - \bar u}}{\sigma }} \right)}^3}} \right]. $ | (7) |
4) 峰度,即标准4阶中心矩
| $ {\text{kurt}}\left( u \right) = \frac{{E{{\left( {{u_i} - \bar u} \right)}^4}}}{{{\sigma ^4}}}. $ | (8) |
5) 结构因子,一般认为,颗粒流化的微观结构影响两相流动的特性,而颗粒微观结构与其瞬时分布有关。有限Reynolds数球形颗粒与流体的相互作用一般呈现明显的各向异性特征,从而可能呈现出各向异性的微观结构。流化系统的微观结构可以采用双分布方程来描述,其傅里叶变换形式即为结构因子[12]
| $ S\left( \mathit{\boldsymbol{\kappa }} \right) = \frac{1}{N}\left\langle {\sum\limits_i {\sum\limits_j {{{\rm{e}}^{ - {\rm{i}}\mathit{\boldsymbol{\kappa }} \cdot {\mathit{\boldsymbol{r}}_{ij}}}}} } } \right\rangle . $ | (9) |
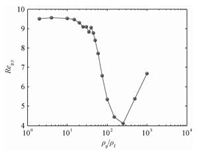
由图 1可知,颗粒平均Reynolds数在低密度比的时候保持一个稳定的数值,随着密度比的增加,在密度比为20左右时,颗粒平均Reynolds数开始减小,到密度比为250时又开始随着密度比的增加而增加。表明颗粒平均速度随颗粒-流体密度比的增加经历一个先减小然后增大的过程。不稳定流动出现在颗粒平均速度开始急剧减小的位置即密度比为20以后。
|
Download:
|
|
图 1 颗粒Reynolds数随密度比的变化 Fig. 1 Particle Reynolds number as a function of density ratio |
|
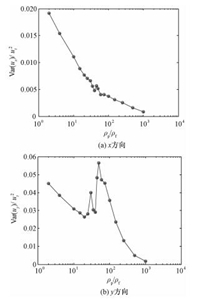
图 2(a)表示水平方向上无量纲化颗粒速度方差随密度比的变化,随着密度比的增加,水平方向无量纲化的颗粒速度方差一直减小,呈现出2个较为明显的衰减斜率,在较低密度比时,衰减斜率较大,在高密度比时,衰减斜率较小。这是由于拥有较大惯性的颗粒不易产生脉动,导致速度方差逐渐减小。图 2(b)表示竖直方向上无量纲化颗粒速度方差随密度比的变化,随着密度比的增加,无量纲化颗粒速度方差先减小,后增大然后再减小。极小值出现在密度比为20左右,极大值在密度比为60左右,然后开始减小。由于竖直方向上颗粒在密度比为60左右形成一种致密的聚团导致较高的方差;随着密度比增加,颗粒聚团变得松散,颗粒更容易跟随聚团运动,竖直方向上颗粒速度方差减小。
|
Download:
|
|
图 2 无量纲化颗粒速度方差随密度比的变化 Fig. 2 Dimensionless particle velocity variance as a function of density ratio |
|
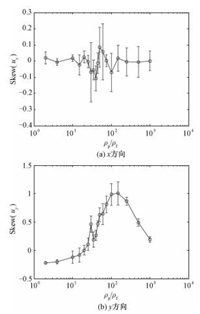
图 3(a)表示水平方向颗粒速度偏度随密度比的变化,随着密度比的增加水平方向上的颗粒速度偏度在零附近上下波动,没有显著变化。由于颗粒在水平方向上不受重力,颗粒在此方向上的速度以较小幅度均匀脉动,速度偏度近似于零。由图 3(b)可知,颗粒在竖直方向上速度偏度随密度比先增加后减小,最大值出现在密度比为150附近。在稳定流动状态下,颗粒速度偏度为负值,随着密度比增加而变为正值。负的偏度表明大部分颗粒速度小于整体平均速度,可能由于系统稳定流化导致的颗粒回流而造成,正值的偏度是由于流出颗粒聚团的颗粒速度大于整体颗粒的平均速度。
|
Download:
|
|
图 3 颗粒速度偏度随密度比的变化 Fig. 3 Particle velocity skewness as a function of density ratio |
|
图 4(a)表示水平方向颗粒速度峰度随密度比的变化,随着密度比的增加,在稳定状态下水平方向上的颗粒速度峰度增加缓慢,当不稳定流动产生以后,迅速增加到达最大值,此处局部颗粒速度分布不均性增强,然后减弱。表明流动不稳定性对水平方向上的颗粒速度有较大影响,在致密聚团阶段局部颗粒流出聚团的速度增大,而在松散聚团阶段,流出聚团的颗粒速度和聚团内部颗粒运动速度的差异减小,导致峰度下降。由图 4(b)可知,稳定流动状态时竖直方向上的颗粒速度峰度维持基本稳定状态,随着密度比的增加而开始减小,在密度比为60时达到最小,然后再增大,表明此处流出颗粒聚团的颗粒速度较聚团内部颗粒速度要大很多,这是由于在致密型聚团的时候,流化通道内形成了竖直方向上流体颗粒相互间隔的流动通道,导致颗粒速度增大。

|
Download:
|
|
图 4 颗粒速度峰度随密度比的变化 Fig. 4 Particle velocity kurtosis as a function of density ratio |
|
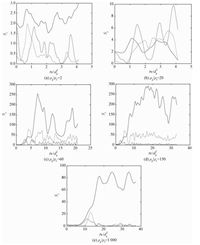
图 5为不同密度比下结构因子随无量纲时间的变化关系。竖直方向上的结构因子在密度比为2的时候,如图 5(a)所示,实线占主导且数值较小,此时系统处于稳定流动结构。密度比为20时,如图 5(b),虽然虚线占主导,且结构因子数值有所增加,但此时系统仍处于稳定流动结构,无明显的聚团形成。当密度比为60(图 5(c)) 和150(图 5(d)) 时,系统形成一个明显的聚团,结构因子的数值迅速增大,表明此时系统内形成一个明显的致密的颗粒聚团。当密度比增加到1 000(如图 5(e)所示) 时,此时虽然形状因子的数值有所降低,但是系统内仍形成一个明显的松散的颗粒聚团结构。通过结构因子分析的结果与前面颗粒速度特性分析结果一致,表明结构因子可用来分析聚团的结构并预测流体-颗粒系统流动由稳定向不稳定的转变。
|
Download:
|
|
图 5 不同密度比下结构因子随时间的变化 Fig. 5 Structure factor variations with dimensionless time at different density ratios |
|
图 6为不同密度比情况下稳定状态时流态化的分布图。低密度比时,颗粒空间位置分布比较均匀,看不到明显的聚团结构。在密度比为60时,流动变得不稳定,有颗粒聚团形成,此时,高浓度区域和低浓度区域中间过渡带比较长。密度比增加到150时,形成明显的颗粒聚团,此时颗粒聚团与分散颗粒有着明显清晰的分界面,稀相颗粒分散较为均匀,颗粒聚团紧致。密度比为500时,颗粒聚团和分散颗粒间的界面不再非常清晰,稀相颗粒浓度增加,聚团的浓度有所减小,聚团变得松散。密度比为1 000时可见聚团内部颗粒浓度进一步降低,聚团更加松散。
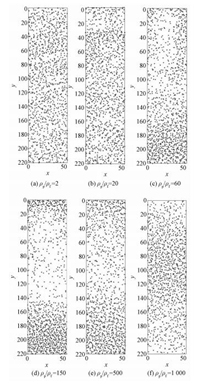
|
Download:
|
|
图 6 不同密度比下瞬时颗粒分布 Fig. 6 Instantaneous particle distributions at different density ratios |
|
通过研究一个流体-颗粒流化系统中的颗粒速度、方差、偏度和峰度及流体速度方差等特性,结合结构因子分析,获得不同密度比下流体-颗粒系统流动由稳定转向不稳定的范围。研究获得如下结论:
1) 研究发现稳定/不稳定的转变可以通过结构因子检测得到,针对本文研究的对象,在密度比大于20的时候其不稳定结构产生。
2) 平均流化速度随着流动不稳定性的产生而开始减小。
3) 水平方向上颗粒速度的方差随着密度比的增加而减小,且在不同聚团结构时减小幅度不同;竖直方向上的颗粒速度方差随密度比的增加先减小后增大,在密度比为60时又开始减小。
4) 水平方向上颗粒速度偏度接近于零;竖直方向上颗粒速度偏度在稳定流动时为负值,当系统不稳定时变为正值,然后随密度比的增加先增大后减小。
5) 水平方向上的颗粒速度峰度随着密度比的增加,在稳定状态下增加缓慢,当聚团结构产生以后,迅速增加到达最大值然后减小。稳定流动状态时竖直方向上的颗粒速度峰度维持基本稳定状态,随着密度比的增加在致密聚团产生时减小,在松弛聚团产生时开始增加。
6) 结构因子的检测结果与分析结果和物理现象吻合良好,表明结构因子可用来分析聚团的结构及预测不稳定状态的产生。
| [1] | Derksen J J, Sundaresan S. Direct numerical simulations of dense suspensions:wave instabilities in liquid-fluidized beds[J]. Journal of Fluid Mechanics, 2007, 587:303–336. |
| [2] | Wen C Y, Yu Y H. Mechanics of fluidization[J]. American Institute of Chemical Engineers Symposium Series, 1966, 62:100–111. |
| [3] | Beetstra R, Van der Hoef M A, Kuipers J A M. A lattice-boltzmann simulation study of the drag coefficient of clusters of spheres[J]. Computers & Fluids, 2006, 35:966–970. |
| [4] | Yang N, Wang W, Li J H. CFD Simulation of concurrent-up gas-solid flow in circulation fluidized beds with structure-dependent drag coefficient[J]. Chemical Engineering Journal, 2003, 96:71–80. DOI:10.1016/j.cej.2003.08.006 |
| [5] | Liu G D, Wang P, Wang S, et al. Numerical simulation of flow behavior of liquid and particles in liquid-solid risers with multi scale interfacial drag method[J]. Advanced Powder Technology, 2013, 24(2):537–548. DOI:10.1016/j.apt.2012.10.007 |
| [6] | Hill R J, Koch D L, Ladd A J C. The first effects of fluid inertia on flows in ordered and random arrays of spheres[J]. Journal of Fluid Mechanics, 2001, 449:213–241. |
| [7] | Mitrano P P, Zenk J R, Benyahia S, et al. Kinetic-theory predictions of clustering instabilities in Granular flows:beyond the small-Knudsen-number regime[J]. Journal of Fluid Mechanics, 2014, 738 R2:1–12. |
| [8] | William D F, Mitrano P P, Li X Q, et al. Validation of a new kinetic theory based two-fluid model for monodisperse gas-solid particulate flows[C]//Japan-US Chemical Engineering, 2015. |
| [9] | 郭照立, 郑楚光. 格子Boltzmann方法的原理及应用[M]. 北京: 科学出版社, 2009. |
| [10] | Ladd A J C. Numerical simulations of particulate suspensions via a discretized Boltzmann equation[J]. Journal of Fluid Mechanics, 1994, 271:285–310. DOI:10.1017/S0022112094001771 |
| [11] | Ladd A J C, Verberg R. Lattice-Boltzmann simulations of particle-fluid suspensions[J]. Journal of Statistical Physics, 2001, 104:1191–1251. DOI:10.1023/A:1010414013942 |
| [12] | Yin X L, Koch D L. Hindered settling velocity and microstructure in suspensions of solid spheres with moderate Reynolds numbers[J]. Physics of Fluids, 2007, 19:19:093302, 1–15. |
 2017, Vol. 34
2017, Vol. 34 


