2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
工业发展使得废水排放量与日俱增,水中有害化学物质和难降解有机物逐年增多,传统水处理方法已无法满足新的环保要求,迫切需要研发新型废水处理方法与技术工艺。空化氧化法作为难降解有机废水处理方法不仅可有效去除许多难降解物质和有毒物质,而且还具有无二次污染、反应装置简单等诸多优点,是近年来比较受关注的新型水处理方法[1-3]。
空化现象指当液体内部局部压力降低至液体温度对应的饱和蒸汽压力时,在液体中或液固界面上蒸汽或气体空穴 (空化泡) 形成、生长及溃灭的过程[4-5]。科学研究表明,空化泡急速溃灭瞬间在液体介质中会形成局部高温高压环境,并伴有强烈冲击波和高速射流,同时释放出1~1 018 kW/m3的高密度能量[6], 该能量能够使空化泡内部的水蒸气在高温、高压下发生裂解反应,产生高活化性的自由基离子和氧化剂[7]。空化泡溃灭形成的微射流使这些自由基和氧化剂进入液相与液体混合,从而与液体中的有机污染物发生氧化反应,将水中大多数有机污染物氧化降解成为无害物质,实现污水处理[8]。
目前国内外关于水力空化处理废水的研究主要集中在宏观层面,研究者多关心水力空化降解对有机污染物的直接效果 (有机物去除率)[9-11],而对水力空化降解有机污染物的微观机理研究较少。水力空化对有机污染物的降解作用源自于空化泡溃灭时形成的具有强氧化性的自由基离子,自由基产量与空化泡溃灭强度息息相关,而空化泡溃灭又离不开其形成和生长过程。因此,要清晰揭示水力空化降解有机污染物的微观机理,必须对空化泡形成、生长及溃灭的动力学过程特性展开深入研究。本文基于考虑液体黏性、表面张力以及可压缩性影响的Gilmore空化泡动力学方程,兼顾水分子扩散及导热的影响,建立湍流作用下孔板空化器下游流场的空化泡动力学模型。基于MATLAB软件平台开发相关计算程序,采用四阶龙格-库塔法求解该空化泡动力学模型,再现空化泡沿流动方向生长、溃灭和反弹的过程,研究液体温度、入口压力、空化泡初始半径对空化泡溃灭温度和压力的影响。在此基础上,基于稳态平衡假设,以空泡内温度、压力、水分子数的变化作为输入参数,采用FactSage软件计算分析空化泡溃灭瞬间自由基离子的产量。
1 数学模型 1.1 空化泡运动驱动压力空化泡的动力学特性是由空化泡周围流场的驱动压力决定的。对于通过孔板的高雷诺数流动, 漩涡的形成会引起速度波动, 从而导致压力波动, 孔板下游压力的恢复不再是线性变化.空化泡的动力学特性将同时受到平均流动和瞬时湍流速度脉动的影响。则孔板下游任意一点 (轴向方向) 在t时刻的瞬时速度可表示为
| $ {v_t} = \overline {{v_t}} + v'\sin \left( {2{\rm{ \mathsf{ π} }}{f_{\rm{T}}}t} \right), $ | (1) |
其中,vt是时均流速,v′是瞬时脉动速度,fT为湍流速度脉动频率, 可通过下列关系式求出:
| $ {P_{\text{M}}} = \frac{{{{\left( {v'} \right)}^3}}}{l}, $ | (2) |
| $ {f_{\text{T}}} = \frac{{v'}}{l}, $ | (3) |
其中,l为湍流涡尺度。根据Prandtl涡长度理论,
| $ l = 0.08{d_x}. $ | (4) |
dx取孔板位置和压力完全恢复位置直径的平均值, 即dx=(d0+dp)/2。d0为孔板孔径,dp为管道直径。PM为湍流耗散率,可表示为
| $ {P_{\text{M}}} = \frac{{\Delta PQ}}{{V\rho }}, $ | (5) |
其中,ΔP为压力损失,由下式给出:
| $ \Delta P = {P_0} - {P_2} + \rho {v_0}^2/2 - \rho {v_{\text{p}}}^2/2. $ | (6) |
其中:v0和vP分别为孔板处和管道内流体的流速;P0和P2为孔板处和液体完全恢复的压力;Q为体积流量;V为孔板下游压力恢复区液体总体积.
| $ V = L \times {{\rm{\pi }}}{d_{\text{p}}}^2/4, $ | (7) |
式中,L是孔板下游压力区的长度,
| $ L = 8{d_{\text{p}}}. $ | (8) |
孔板下游的压力可以根据伯努利方程获得:
| $ \begin{array}{*{20}{c}} {{P_t} = {P_0} + \frac{1}{2}\rho \left( {{v_0}^2 - {v_t}^2} \right) - } \\ {\left\{ {\Delta P\left( {\frac{t}{\tau }} \right) - k\Delta P{{\left( {\frac{t}{\tau }} \right)}^{\frac{2}{3}}}} \right\},} \end{array} $ | (9) |
| $ k = 0.5 \times {\rho ^{1/3}}{\left( {\frac{Q}{V}l} \right)^{2/3}}, $ | (10) |
其中,τ为压力完全恢复的时间:
| $ \tau = \frac{L}{{\frac{1}{2}\left( {{v_0} + {v_{\text{p}}}} \right)}}. $ | (11) |
对于本文模型, 采用以下假设:1) 空化泡膨胀和收缩期间保持为球形;2) 忽略液体相与空化泡之间的相对运动,空化泡形成以后保持力学平衡;3) 空化泡内气体由水蒸气和氩气组成,氩气扩散的时间尺度远大于空化泡振荡的时间尺度,其影响可以忽略;4) 空化泡内化学反应时间尺度远小于空化泡振荡的时间尺度,化学反应对空化泡动力学的影响可以忽略。
1.2.1 泡壁运动控制方程采用考虑了液体黏性、表面张力及可压缩性影响的Gilmore方程:
| $ \begin{array}{*{20}{c}} {\left( {1 - \frac{1}{c}\frac{{{\text{d}}R}}{{{\text{d}}t}}} \right)R\frac{{{{\text{d}}^2}R}}{{{\text{d}}{t^2}}} + \frac{3}{2}\left( {1 - \frac{1}{{3c}}\frac{{{\text{d}}R}}{{{\text{d}}t}}} \right){{\left( {\frac{{{\text{d}}R}}{{{\text{d}}t}}} \right)}^2} = } \\ {\left( {1 - \frac{1}{c}\frac{{{\text{d}}R}}{{{\text{d}}t}}} \right)H + \frac{R}{c}\left( {1 - \frac{1}{c}\frac{{{\text{d}}R}}{{{\text{d}}t}}} \right)\frac{{{\text{d}}H}}{{{\text{d}}t}},} \end{array} $ | (12) |
其中:R为t时刻空化泡半径,c为液体中的局部声速,H为泡壁处液体的焓值。
| $ c = {c_\infty }{\left( {\frac{{{P_{\text{R}}} + B}}{{{P_t} + B}}} \right)^{\frac{{n - 1}}{{2n}}}}, $ | (13) |
| $ \begin{array}{*{20}{c}} {H = \int_{{p_t}}^{{P_{\text{R}}}} {{{\left( {\frac{{{P_{\text{R}}} + B}}{{{P_t} + B}}} \right)}^{ - \frac{1}{n}}}} \frac{{{\text{d}}P}}{\rho } = } \\ {\frac{{m\left( {{P_t} + B} \right)}}{{\left( {n - 1} \right)\rho }}\left[ {{{\left( {\frac{{{P_{\text{R}}} + B}}{{{P_t} + B}}} \right)}^{\frac{{n - 1}}{{2n}}}} - 1} \right].} \end{array} $ | (14) |
其中:c∞为未受扰动的液体中声速;n和B是常量;PR是泡壁处的压力。
| $ {P_{\text{R}}} = {P_i} - \frac{{2\sigma }}{R} - \frac{{4\mu }}{R}\frac{{{\text{d}}R}}{{{\text{d}}t}}. $ | (15) |
液体表面张力系数σ, 液体黏度系数μ,根据液体温度T0给出,Pi是根据范德瓦尔斯方程给出的泡内气体压力。
| $ {P_i} = \frac{{{N_{{\text{tot}}}}\left( t \right)kT\left( t \right)}}{{\frac{{4{{\rm{\pi }}}}}{3}\left( {{R^3}\left( t \right) - {{\left( {{R_0}/8.86} \right)}^3}} \right)}}, $ | (16) |
其中:Ntot是泡内分子总数;T是泡内气体温度,R0是空化泡在液体中的平衡半径。
1.2.2 泡壁热质传递模型在空化泡溃灭过程中的高温高压条件下,液体中溶解的少量氮气、氧气、二氧化碳等,会转变成无机离子溶解于水,而逐渐被消耗殆尽。在不易分解的稀有气体中,氩气含量最为丰富,因此,本文假设空化泡内气体主要由水蒸气和氩气组成。氩气含量根据气泡初始时的平衡条件,氩气的分子数通过初始泡壁平衡条件给出,NAr=4×π/3×R03T0/k。氩气扩散的时间尺度远大于空化泡振荡的时间尺度,其影响可以忽略。泡内水分子数的变化描述如下:
| $ \frac{{{\rm{d}}{N_{\rm{w}}}}}{{{\rm{d}}t}} = 4{\rm{ \mathsf{ π} }}{R^2}D\frac{{{n_{\rm{R}}} - {n_{\rm{w}}}}}{{{l_{{\rm{diff}}}}}},{l_{{\rm{diff}}}} = \min \left( {\sqrt {\frac{{RD}}{{\left| {{\rm{d}}R/{\rm{d}}t} \right|}}} ,\frac{R}{{\rm{ \mathsf{ π} }}}} \right), $ | (17) |
式中:nR是泡壁处水分子数密度:nw是气泡内实际的水分子数密度, nw=Nw/(4×π/3×R3);ldiff是扩散边界层厚度;D是水分子扩散系数,根据Chapman-Enskog理论计算得到[12]。
与质量传递相似,通过泡壁的导热可以由下式估算:
| $ \frac{{{\rm{d}}Q}}{{{\rm{d}}t}} = 4{\rm{ \mathsf{ π} }}{R^2}\lambda \frac{{{T_0} - T}}{{{l_{{\rm{th}}}}}},{l_{{\rm{th}}}} = \min \left( {\sqrt {\frac{{R\chi }}{{\left| {{\rm{d}}R/{\rm{d}}t} \right|}}} ,\frac{R}{{\rm{ \mathsf{ π} }}}} \right), $ | (18) |
式中:λ是泡内气体混合物的热导率,由文献[13]给出的公式求得;lth是热边界层厚度;χ是热扩散率;χ=λ/(ρArCp, Ar+ρwCp, w),ρAr和ρw分别是氩气和水蒸气的分子数密度。氩气和水蒸气分子的比热容根据下式计算:
| $ _{{\text{p}},{\text{Ar}}} = \frac{5}{2}{N_{{\text{Ar}}}}k, $ | (19) |
| $ {C_{{\text{p}},{\text{w}}}} = {N_{\text{w}}}k\left( {4 + \sum {\frac{{\left( {{\theta _i}/2T} \right)}}{{{{\sinh }^2}\left( {{\theta _i}/2T} \right)}}} } \right). $ | (20) |
式中:k是玻尔兹曼常数;θ是水分子振荡特征温度,θ1=2 295 K,θ2=5 255 K,θ3=5 400 K。
1.2.3 能量守恒方程根据开口系统热力学第一定律,空化泡内部总的能量守恒方程为
| $ \frac{{{\text{d}}E}}{{{\text{d}}t}} = \frac{{{\text{d}}Q}}{{{\text{d}}t}} - {P_i}\frac{{{\text{d}}V}}{{{\text{d}}t}} + {h_{\text{w}}}\frac{{{\text{d}}{N_{\text{w}}}}}{{{\text{d}}t}}, $ | (21) |
式中:hw=4kT0是从气液交界面进入泡内的水分子焓值;E是泡内气体内能,可表示为泡内温度和分子数的函数:
| $ E = \frac{3}{2}{N_{{\text{Ar}}}}kT + \left( {\frac{6}{2} + \sum {\left( {\frac{{{\theta _i}/T}}{{{{\text{e}}^{{\theta _i}/T}} - 1}}} \right)} } \right){N_{\text{w}}}kT. $ | (22) |
将方程 (12) 代入能量守恒方程,得到泡内温度随时间的变化:
| $ \begin{array}{*{20}{c}} {\frac{{{\rm{d}}T}}{{{\rm{d}}t}} = \frac{1}{{{C_{\rm{v}}}}}\frac{{{\rm{d}}Q}}{{{\rm{d}}t}} - \frac{{{P_i}}}{{{C_{\rm{v}}}}}\frac{{{\rm{d}}V}}{{{\rm{d}}t}} + } \\ {\frac{1}{{{C_{\rm{v}}}}}\left( {4{T_0} - 3T - T\sum {\left( {\frac{{{\theta _i}/T}}{{{{\rm{e}}^{{\theta _i}/T}} - 1}}} \right)} } \right)\frac{{{\rm{d}}{N_{\rm{w}}}}}{{{\rm{d}}t}}k,} \end{array} $ | (23) |
其中
| $ {C_{\text{v}}} = \frac{3}{2}{N_{{\text{Ar}}}}k + \left( {\frac{6}{2} + \sum {\left( {\frac{{{{\left( {{\theta _i}/T} \right)}^2}{{\text{e}}^{{\theta _i}/T}}}}{{{{\left( {{{\text{e}}^{{\theta _i}/T}} - 1} \right)}^2}}}} \right)} } \right){N_{\text{w}}}k. $ | (24) |
空化泡溃灭的时间尺度远小于水分子扩散和在泡壁处凝结的时间尺度,因此空化泡溃灭瞬间大量水分子留在空化泡内部。水分子在高温高压环境中发生一系列热解反应,产生自由基离子。由于化学反应的时间尺度要远小于空化泡振荡的时间尺度,因此假设空化泡溃灭瞬间,其内部保持热力学平衡状态。基于稳态平衡假设,应用吉布斯自由能最小原理,采用FactSage软件中的Equilib模块对空化泡溃灭瞬间反应产物和成分进行分析和计算。由于温度对泡内自由基生成影响较大,空化泡第一次溃灭瞬间,泡内温度最高,此时化学反应最为剧烈,因此仅对该时刻泡内的产物成分进行分析。模拟的输入条件为泡内温度、压力和水分子数,这些参数通过对前述空化泡动力学方程求解获得。
2 数值方法方程 (12)、(17)、(18)、(23) 构成描述泡壁运动的封闭方程组。由方程 (17)、(18) 和 (23) 得到气泡内的温度和分子数,再将其代入方程 (16) 得到泡内气体压力,进而根据方程 (15) 得到泡壁处压力。将泡壁压力和方程 (9) 所示的液体瞬时静压Pt代入泡壁动力控制方程 (12) 中,并将方程 (12) 所示的二阶非线性常微分方程转化为一阶常微分方程组,然后利用变步长的四阶龙格-库塔法对该方程组进行求解。本文将水作为液体空化介质, 初始条件设定为: t=0时,R=R0, dR/dt=0, Nw=0,T=T0。孔板流动的入口压力,初始流速以及空化数根据参考文献[14]给出。
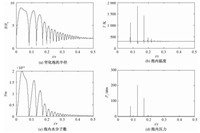
3 结果与讨论 3.1 空化泡动力学特征及溃灭时自由基产量图 1为湍流压力场驱动下初始半径R0=50 μm的空化泡半径和泡内温度、压力、水分子数随无量纲时间 (t/τ,τ为压力完全恢复所需时间) 的变化曲线。计算参数为:P2=1 atm,dP=25 mm,d0=0.5,入口压力P1=4.84 atm, 管内平均流速为33.58 m/s, 空化数Ci=0.099(Ci的定义见文献[14]),T0=293 K。
|
Download:
|
|
图 1 (a) 空化泡的半径; (b) 泡内温度; (c) 泡内水分子数; (d) 泡内压力随无量纲时间变化曲线 Fig. 1 Variations in bubble radius (a), temperature inside bubble (b), pressure inside the bubble (c), and number of water molecules (d) with non-dimensional time |
|
湍流脉动作用下,孔板下游液体压力呈波浪形恢复[5], 在该压力场驱动下, 空化泡最初膨胀然后开始收缩, 此后做振荡运动。空化泡在溃灭瞬间,体积达到最小值,泡内气体压力急剧升高,泡壁的巨大动能将转换为泡内气体的热能。由于热能在瞬间难以散失,气体温度在瞬间升高到极高值。大量水分子在空化泡膨胀过程中进入空化泡内部,而在溃灭瞬间这些水分子并不能完全扩散出空化泡,而是在高温高压条件下发生分解反应,产生自由基离子。表 1是通过FactSage软件计算得到的空化泡第一次溃灭瞬间泡内气体成分及其摩尔浓度,其中具有极强氧化性的·OH浓度可高达0.485 mol/m3,这些羟基自由基扩散到空化泡周围液体中或者直接在泡内与有机物发生氧化还原反应,生成无机物离子和气体,可实现污水中有机污染物的去除。羟基自由基的产量主要与溃灭温度和压力相关,而溃灭温度的影响更加显著[15]。空化泡溃灭温度和压力受到孔板管道入口压力、空化泡初始半径、液体温度等因素的影响。
|
|
表 1 溃灭瞬间空化泡内气体密度 Table 1 Densities of gases inside the bubble at bubble collapse |
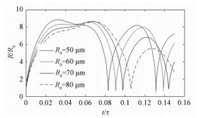
我们模拟参考文献[14]中的2.9、3.87、4.84和5.8 atm等4个进口压力条件,管内平均流速分别为26.5、31.84、33.58和37.89 m/s, 空化数分别为0.161、0.112、0.099和0.079。图 2是空化泡振荡过程中,不同管道入口压力条件下,空化泡半径随无量纲时间的变化曲线。由图中可以看出,随着入口压力的增大,空化泡半径膨胀比增加,空化泡溃灭更加迅速,而泡壁反弹过程中,达到的最大膨胀比也显著增加。表 2给出不同管道入口压力条件下溃灭温度、溃灭压力、泡内水分子和水蒸气分解产生的羟基自由基浓度。

|
Download:
|
|
图 2 不同入口压力下空化泡半径随无量纲时间变化曲线 Fig. 2 Variation in bubble radius with non-dimensional time under different inlet pressures |
|
|
|
表 2 不同入口压力下的溃灭温度,溃灭压力,泡内水分子数和羟基自由基产量 Table 2 Collapse temperature, pressure, and number of water molecules and production of hydroxyl radicals under different inlet pressures |
从表 2可以看出,随着管内进口压力升高,溃灭温度和溃灭压力变大,泡内水分子浓度增加,羟基自由基浓度增大。这是由于随着进口P1升高,管内液体流速增大,孔板下游流场的平均压力梯度和湍流脉动压力变大,液体压力损失与单位质量液体的能量耗散率增加[5]。因此空化泡膨胀比变大,而空化泡收缩速率加快, 溃灭温度升高;同时由于更多水分子在泡壁收缩过程中没有足够时间扩散到溶液中,溃灭瞬间泡内水分子数和溃灭压力增加。泡内水蒸气分解反应速率随着溃灭温度和压力升高而加快,羟基自由基产量增大。参考文献[14]中,随着入口压力从2.9 atm增加到5.8 atm过程中,罗丹明B的降解率增大,这主要是羟基自由基浓度增大引起的,与本文计算结果相符。而入口压力进一步增大到5.8 atm后,罗丹明B降解速率反而降低,这是由于大量空化泡共同作用过程中,空化泡之间的作用力产生缓冲效应,造成泡壁运动速度降低,溃灭温度和压力减小,这在参考文献中有所提及。但是,由于本文基于单空泡动力学模型,为简化计算,忽略了空化泡间的相互作用力,因此,没有捕捉到这种空化泡间的缓冲作用。考虑空泡间的相互作用力的空泡群理论,仍有待进一步研究。
3.3 空化泡初始半径的影响图 3所示为空化泡初始半径对空化泡半径变化情况的影响。表 3给出不同初始半径条件下,溃灭温度、溃灭压力、泡内水分子和羟基自由基浓度的变化情况。
|
Download:
|
|
图 3 不同空化泡初始半径条件下空化泡半径随无量纲时间变化曲线 Fig. 3 Variation in bubble radius with non-dimensional time under different initial bubble radii |
|
|
|
表 3 不同空化泡初始半径溃灭温度,溃灭压力,泡内水分子数和羟基自由基产量 Table 3 Collapse temperature, pressure, number of water molecules and production of hydroxyl under different initial bubble radii |
由图 3看出,当空化泡半径R0从50 μm增大到80 μm过程中,空化泡膨胀比降低,泡壁运动周期变长,泡壁运动速率减小。因而,空化泡溃灭温度和溃灭压力均下降,溃灭时泡内水分子浓度也降低,羟基自由基产量下降。分析其原因,是由于随着空化泡初始半径增大,空化初生时泡内气体压力 (2σ/R0) 减小,导致空化泡膨胀比和泡壁运动速率降低。实际实验过程中,液体内的气核半径分布规律受到液体理化性质和不凝性气体含量等因素影响,目前对其准确测量还比较困难;但是可以通过改变液体温度、增加不凝性气体等方法,调整气核半径分布规律,从而改变空化泡初始半径,使得空化效果增强,自由基产量增加。
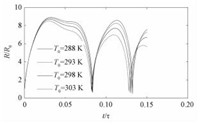
3.4 液体温度的影响图 4为不同初始温度下空化泡半径变化曲线。表 4给出溃灭温度、溃灭压力、泡内水分子和羟基自由基浓度的随液体温度变化情况。
|
Download:
|
|
图 4 不同液体温度条件下空化泡半径随无量纲时间变化曲线 Fig. 4 Variation in bubble radius with non-dimensional time at different liquid temperatures |
|
|
|
表 4 不同液体温度条件下溃灭温度,溃灭压力,泡内水分子数和羟基自由基产量 Table 4 The collapse temperature, pressure, and number of water molecules and production of hydroxyl radicals at different liquid temperatures |
液体的密度、黏度、表面张力系数和饱和蒸汽压力均受到液体温度的影响,而饱和蒸汽压力受温度的影响最为显著[15]。当液体温度从288 K升高到303 K时,饱和蒸汽压力从1 705 Pa升高到4 249 Pa。从图 4可以看出,空化泡膨胀比降低。空化泡溃灭温度从2 179.2 K下降到741.8 K,溃灭压力则从308.78 atm下降到24.43 atm,而泡内水分子数和分解产生的羟基自由基浓度均降低。分析其原因,是由于液体温度升高,对应的饱和蒸汽压力升高,孔板处液体压力也升高,流场压力梯度减小,湍流强度降低,空化泡膨胀和收缩速率降低 (图 4),因此溃灭温度和溃灭压力降低,水蒸气分解速率减小,分解产生的羟基自由基体积分数减小。
4 结论本文以水为工作介质, 对湍流作用下可压缩液体中空化泡动力学行为特性和空化泡溃灭瞬间羟基自由基产量进行数值模拟, 并与实验结果对比,得出以下结论:
1) 管内入口压力增大,溃灭温度和溃灭压力升高,溃灭瞬间泡内水分子浓度增加,分解产物羟基自由基的产量增加。
2) 空化泡初始半径减小,溃灭温度升高,溃灭压力也显著增加,泡内水分子浓度增多,因此分解产生的羟基自由基含量增加。
3) 液体温度主要通过影响饱和蒸汽压力,进而影响空化泡膨胀压缩比,从而影响空化强度。液体温度降低,溃灭温度和压力升高,泡内水分子的浓度减小。
本文针对实验中的单孔板结构,对孔板下游流场中单空泡水力空化现象进行初步研究,对空化泡内羟基自由基产量进行预测。实际空化现象是由大量空化泡共同作用下产生的,空化泡间的相互作用力影响空化泡溃灭强度,进而影响溶液中羟基自由基产量,有关空泡群现象中的自由基产量需要在此基础上,进一步深入研究。此外,基于CFD模拟,可以得到多孔板下游流场速度和压力分布,进而获得空化泡运动的驱动压力,作为本文空化泡动力学模型的输入条件,可以对多孔板水力空化现象进行进一步研究。
| [1] | Gogate P R. Cavitation:an auxiliary technique in waste water treatment schemes[J]. Advances in Environmental Research, 2002, 6(3):335–358. DOI:10.1016/S1093-0191(01)00067-3 |
| [2] | Eilers R. Hydrodynamic cavitation oxidation destroys organics[EB/OL]//EPA Groundwater Currents. (1994-03)[2016-05-20]. http://clu-in.org/download/newsltrs/gwc0394.pdf. |
| [3] | Gogate P R, Pandit A B. A review and assessment of hydrodynamic cavitation as a technology for the future[J]. Ultrasonics Sonochemistry, 2005, 12(1/2):21–27. |
| [4] | 蔡军, 淮秀兰, 闫润生, 等. 湍流作用下水力空化气泡内温度演变的动力学分析[J]. 科学通报, 2011, 56(12):947–955. |
| [5] | 蔡军, 淮秀兰, 李勋锋. 湍流作用下可压缩液体中空化泡的动力学特性[J]. 科学通报, 2010, 55(10):857–866. |
| [6] | Didenko Y T, Suslick K S. The energy efficiency of formation of photons, radicals and ions during single-bubble cavitation[J]. Nature, 2002, 418(6896):394–397. DOI:10.1038/nature00895 |
| [7] | Storey B D, Szeri A J. Water vapour, sonoluminescence and sonochemistry[J]. Proceedings of the Royal Society A, 2000, 456(1999):1685–1709. DOI:10.1098/rspa.2000.0582 |
| [8] | Gogate P R. Treatment of wastewater streams containing phenolic compounds using hybrid techniques based on cavitation:a review of the current status and the way forward[J]. Ultrasonics Sonochemistry, 2008, 15(1):1–15. DOI:10.1016/j.ultsonch.2007.04.007 |
| [9] | Wang J A, Wang X K, Guo P Q, et al. Degradation of reactive brilliant red K-2BP in aqueous solution using swirling jet-induced cavitation combined with H2O2[J]. Ultrasonics Sonochemistry, 2011, 18(2):494–500. DOI:10.1016/j.ultsonch.2010.08.006 |
| [10] | Saharan V K, Pandit A B, Kumar P S, et al. Hydrodynamic cavitation as an advanced oxidation technique for the degradation of acid red 88 Dye[J]. Industrial & Engineering Chemistry Research, 2011, 51(4):1981–1989. |
| [11] | Saharan V K, Rizwani M A, Malani A A, et al. Effect of geometry of hydrodynamically cavitating device on degradation of orange-G[J]. Ultrasonics Sonochemistry, 2013, 20(1):345–353. DOI:10.1016/j.ultsonch.2012.08.011 |
| [12] | Cussler E L. Diffusion:mass transfer in fluid systems[M]. Cambridge: Cambridge University Press, 2009. |
| [13] | Hirschfelder J O, Curtiss C F, Bird R B, et al. Molecular theory of gases and liquids[M]. New York: Wiley, 1954. |
| [14] | Yasui K, Tuziuti T, Sivakumar M, et al. , Theoretical study of single-bubble sonochemistry[J]. The Journal of Chemical Physics, 2005, 122(22):224706. DOI:10.1063/1.1925607 |
| [15] | Cai J, Huai X L, Li X F. Dynamic behaviors of cavitation bubble for the steady cavitating flow[J]. Journal of Thermal Science, 2009, 18(4):338–344. DOI:10.1007/s11630-009-0338-4 |
 2017, Vol. 34
2017, Vol. 34 


