电容层析成像技术 (ECT) 由于其无辐射、非接触、非侵入、成像速度快且成本低等优点[1],目前已经广泛应用于不同领域的多相流动测量过程中[2-9],包括原油管道中的油/气两相流以及火焰、气力输送和循环流化床内的气固两相流等。
与单电极激励方式相比,多电极激励方式可增加独立测量数目,减小逆问题的不适定性。另外,还可提高测量信号的强度,增加测量电容值,有利于电容数据的采集。在传统的二维ECT (2D ECT) 测量过程中,多电极激励方式已经得到广泛关注,相关学者对其稳定性进行了研究。Ye等[10]在一个矩形电容传感器中比较单电极激励、双电极激励和四电极激励3种测量模式。结果表明:在无噪声干扰的情况下,单电极激励方式成像效果最佳;在施加噪声的情况下,双电极激励方式成像效果更加稳定。本文构建了一个包含12个电极 (3层,每层布置4个电极) 的三维ECT (3D ECT) 传感器,并将多电极激励模式应用于3D ECT传感器,分别研究单电极激励模式、同层相邻双电极激励模式和不同层双电极激励模式。之后,对测量的电容数据施加噪声干扰,并进行相关分析,研究3种激励方式对噪声干扰的稳定性。
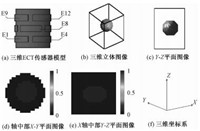
1 三维ECT模型及激励方式 1.1 3D ECT模型如图 1(a)所示,构建一个包含12电极的3D ECT模型。电极分3层布置,每层含4个电极,且中间层相较于其他两层旋转45°。模型管道内径40 mm,壁厚2 mm,高50 mm,被重建的球体直径为10 mm。电极宽度设置为8 mm,使得被测球体能在传感器的有效成像区域。为保证成像质量,电极覆盖率设计约为80%,电极长度29.45 mm,径向距离5.9 mm。为了与电极的径向距离保持一致,电极的轴向距离设置为6 mm。
|
Download:
|
|
图 1 仿真模型 Fig. 1 Simulation model |
|
传统的单电极激励方式可以描述为:电极E1施加激励,测量E2~E12共11个电极上的电荷量;之后电极E2施加激励,测量E3~E12共10个电极的电荷量;然后依次对其余电极施加激励,直至电极E11施加激励,测量E12电极上的电荷量,共可得到66个电容值。
多电极激励方式可以增加测量数目,且可以提高激励信号的强度。因此,本文对同层相邻双电极激励方式进行研究,在测量过程中对同层相邻电极进行激励,采集其余极板电荷量,这样共可得到120个电容值。
为改善敏感场均匀性,本文设置不同层双电极激励模式,即对位于不同层上的2个电极施加激励,测量其余极板电荷量。以1、2层平面为例,对E1~E5,E2~E6,E3~E7,E4~E8电极依次施加激励,测量其余电极电荷量。这种方式共可得到120个电容值。
本文研究的3种激励测量方式如表 1所示。
|
|
表 1 激励测量方式 Table 1 Excitation strategies |
ECT的近似线性数学模型[11]可以表示为
| $ \mathit{\boldsymbol{\lambda }} = \mathit{\boldsymbol{Sg}}, $ | (1) |
其中:λ为归一化电容向量,S为归一化灵敏度矩阵,g为归一化介电常数向量。
在3D ECT中,灵敏度矩阵元素由下式计算
| $ \begin{array}{*{20}{c}} {{S_{ij}}\left( {x,y,z} \right) = - \iiint_p {\frac{{\nabla {\varphi _i}\left( {x,y,z} \right)}}{{{V_i}}}}.} \\ {\frac{{\nabla {\varphi _i}\left( {x,y,z} \right)}}{{{V_j}}}{\rm{d}}x{\rm{d}}y{\rm{d}}z,} \end{array} $ | (2) |
其中:Sij(x, y, z) 为电极i和j在区域p上的灵敏度,φi(x, y, z) 为电极i施加电压Vi且其余电极接地时的电势分布。
归一化电容值[12]可以表示为
| $ \mathit{\boldsymbol{\lambda }} = \frac{{{\mathit{\boldsymbol{C}}^m} - {\mathit{\boldsymbol{C}}^l}}}{{{\mathit{\boldsymbol{C}}^h} - {\mathit{\boldsymbol{C}}^l}}}, $ | (3) |
其中,λ为归一化电容值,Cm为测量所得电容值,Ch和Cl分别为满场电容值和空场电容值。本文中,满场时内部相对介电常数为3,空场时内部相对介电常数为1。
2.2 图像重构算法为解决ECT逆问题,计算测量区域的介电常数值,研究人员提出多种重构算法。在迭代算法中,Landweber迭代算法[11]应用最为广泛,其计算公式为
| $ {\mathit{\boldsymbol{g}}^n} = {\mathit{\boldsymbol{g}}^{n - 1}} + {\alpha ^n}{\mathit{\boldsymbol{S}}^{\rm{T}}}\left( {\mathit{\boldsymbol{\lambda }} - \mathit{\boldsymbol{S}}{\mathit{\boldsymbol{g}}^{n - 1}}} \right), $ | (4) |
其中,αn为迭代步长[13]
| $ {\alpha ^n} = \frac{{{{\left\| {{\mathit{\boldsymbol{S}}^{\rm{T}}}{\mathit{\boldsymbol{e}}^{\left( {n - 1} \right)}}} \right\|}^2}}}{{{{\left\| {\mathit{\boldsymbol{S}}{\mathit{\boldsymbol{S}}^{\rm{T}}}{\mathit{\boldsymbol{e}}^{\left( {n - 1} \right)}}} \right\|}^2}}}, $ | (5) |
e(n-1)表示测量电容与计算电容之间的误差[11]
| $ {\mathit{\boldsymbol{e}}^{\left( {n - 1} \right)}} = \mathit{\boldsymbol{\lambda }} - \mathit{\boldsymbol{S}}{\mathit{\boldsymbol{g}}^{\left( {n - 1} \right)}}. $ | (6) |
本文应用上述算法重构,迭代步数统一为20。
3 模拟条件设置本文中,测量区域划分为20×20×25,圆柱区域内共7 900个像素。如图 1(b)~1(e)所示,本文在测量区域中心处设置一个半径为10 mm的球体,为高介电常数分布。
相关系数作为本文图像质量评价标准[11]
| $ r = \frac{{\sum\limits_{i = 1}^{{N_k}} {\left( {{g_i} - \bar g} \right)\left( {{{\hat g}_i} - \overline {\hat g} } \right)} }}{{\sqrt {\sum\limits_{i = 1}^{{N_k}} {{{\left( {{g_i} - \bar g} \right)}^2}} \sum\limits_{i = 1}^{{N_k}} {{{\left( {{{\hat g}_i} - \overline {\hat g} } \right)}^2}} } }}, $ | (7) |
其中:r为相关系数,gi为真实分布中i点像素值,ĝi为重构图像中i点像素值,g为真实分布中像素平均值,ĝ为重构图像的像素平均值,Nk为测量区域内像素总数。
4 模拟结果及分析为研究噪声干扰对3种激励方式的影响,本文分别设置了无噪声干扰,振幅为1 fF的噪声干扰和振幅为2 fF的噪声干扰3种情况。
4.1 无噪声干扰图 2为无噪声干扰下3种测量方式所得结果。从图中可以看出:测量方式1所得图像更接近于真实分布,边界也更加明显;测量方式3重构效果次于测量方式1,但优于测量方式2。由表 2相关系数数据可以得到:测量方式1相关系数最大,测量方式2相关系数最小。由以上结果可知,无噪声干扰情况下,测量方式1即单电极激励方式成像效果最佳。

|
Download:
|
|
图 2 无噪声干扰信号所重构的图像 Fig. 2 Reconstructed images by using noise-free data |
|
|
|
表 2 无噪声干扰信号所得结果相关系数 Table 2 Correlation coefficients under noise-free data |
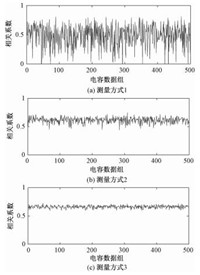
为研究不同激励方式的测量稳定性,本文对原始电容数据施加了振幅为1 fF的噪声干扰,并得到500组含噪声数据。利用含噪声数据进行图像重建并计算所得图像的相关系数,如图 3所示。从图中可以明显看出:测量方式1所得相关系数波动幅度最大,测量方式3波动幅度最小。
|
Download:
|
|
图 3 振幅为1fF的噪声干扰信号所得相关系数 Fig. 3 Correlation coefficients under noisy data with 1fF amplitude |
|
根据图 3数据,表 3对3种测量方式下各500组数据的相关系数进行数据分析,分别得到最大值、最小值、平均值及标准差。由表 3可知,测量方式3所得相关系数的平均值最大且标准差最小,表明不同层双电极激励方式受噪声影响最小、稳定性最好。
|
|
表 3 振幅为1fF的噪声干扰信号所得结果相关系数分析 Table 3 Analysis of correlation coefficients under noisy data with 1fF amplitude |
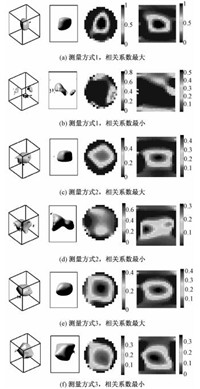
图 4为取相关系数最大和最小情况所得图像。从图中可以看出,取相关系数最小的电容数据进行图像重构时,测量方式1和测量方式2所重构图像已经不能反映真实分布,而测量方式3所重构图像尽管质量下降,但仍能反映真实分布。
|
Download:
|
|
图 4 振幅为1fF噪声干扰下重构图像 Fig. 4 Reconstructed images by using noisy data with 1fF amplitude |
|
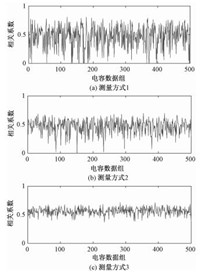
对原始电容数据施加振幅为2fF的噪声干扰,得到500组含噪声数据。对上述数据继续做相关性分析,结果见图 5。与振幅为1fF的噪声干扰结果相同,测量方式1相关系数波动幅度最大,测量方式3相关系数波动幅度最小。
|
Download:
|
|
图 5 振幅为2fF的噪声干扰信号所得相关系数 Fig. 5 Correlation coefficients under noisy data with 2fF amplitude |
|
根据图 5数据,表 4对3种测量方式下各500组数据的相关系数进行数据分析,分别得到最大值、最小值、平均值及标准差。由表 4可知,测量方式3所得相关系数的平均值最大且标准差最小,表明不同层双电极激励方式受噪声影响最小、稳定性最好。
|
|
表 4 振幅为2fF的噪声干扰信号所得结果相关系数分析 Table 4 Analysis of correlation coefficients under noisy data with 2fF amplitude |
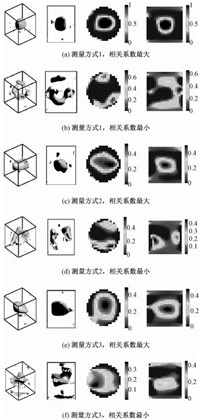
图 6为取相关系数最大和最小情况所得图像。从图中可以看出,取相关系数最小的电容数据进行图像重构时,测量方式1和测量方式2所重构图像已经不能反映真实分布,而测量方式3所重构图像仍能大致反映真实分布。
|
Download:
|
|
图 6 振幅为2fF噪声干扰下重构图像 Fig. 6 Reconstructed images by using noisy data with 2fF amplitude |
|
本文研究3种激励测量模式,即单电极激励、同层相邻双电极激励和不同层双电极激励,在三维ECT测量中的性能。通过对原始测量数据施加不同程度的噪声干扰,对结果稳定性进行分析。针对本文中设置的流型,得到下述结论,
1) 无噪声干扰时,单电极激励方式成像效果最佳;
2) 存在噪声干扰时,不同层双电极激励方式成像效果最稳定,单电极激励方式波动幅度最大。
此外,本文只设置了中心区域为高介电常数的流型,对其他流型仍需要进一步研究。
| [1] | Yang W Q. Design of electrical capacitance tomography sensors[J]. Measurement Science and Technology, 2010, 21(4):042001. DOI:10.1088/0957-0233/21/4/042001 |
| [2] | Sun J T, Yang W Q. A dual-modality electrical tomography sensor for measurement of gas-oil-water stratified flows[J]. Measurement, 2015, 66(1):150–160. |
| [3] | 孙猛, 刘石, 雷兢, 等. 利用电容层析成像法测量气力输送中的煤粉流量[J]. 动力工程, 2008, 28(3):411–414. |
| [4] | Wang X X, Hu H L, Liu X, et al. Concentration measurement of dilute pulverized fuel flow by electrical capacitance tomography[J]. Instrumentation Science & Technology, 2015, 43(1):89–106. |
| [5] | 王海刚, 赵国荣, 邱桂芝. 循环流化床多旋风分离器入口电容层析成像测量[J]. 工程热物理学报, 2014, 35(1):109–113. |
| [6] | Zhang R H, Wang Q, Wang H X, et al. Data fusion in dual-mode tomography for imaging qil-gas two-phase flow[J]. Flow Measurement and Instrumentation, 2014, 37(1):1–11. |
| [7] | Zhao T, Liu K, Murata H, et al. Experimental and numerical investigation of particle distribution behaviors in a rolling circulating fluidized Bed[J]. Powder Technology, 2014, 258(1):38–48. |
| [8] | Andrew H. Weighing without touching:applying electrical capacitance tomography to mass flowrate measurement in multiphase flows[J]. Measurement & Control, 2014, 47(1):19–25. |
| [9] | Eso A A, Zhao Y B, Yeung H. Comparison of electrical capacitance tomography & gamma densitometer measurement in viscous oil-gas flows[C]//8th International Symposium on Measurement Techniques for Multiphase Flows. Guangzhou, China:AIP Conf Proc. 2014:81-89. |
| [10] | Ye J M, Ge R H, Qiu G Z, et al. Measurement strategy for rectangular electrical capacitance tomography sensor[C]//8th International Symposium on Measurement Techniques for Multiphase Flows. Guangzhou, China:AIP Conf Proc. 2014:37-42. |
| [11] | Yang W Q, Peng L H. Image reconstruction algorithms for electrical capacitance tomography[J]. Measurement Science and Technology, 2003, 14(1):R1–R13. DOI:10.1088/0957-0233/14/1/201 |
| [12] | Ye J M, Wang H G, Yang W Q. A sparsity reconstruction algorithm for electrical capacitance tomography based on modified landweber iteration[J]. Measurement Science and Technology, 2014, 25(11):115402. DOI:10.1088/0957-0233/25/11/115402 |
| [13] | Liu S, Fu L, Yang W Q. Optimization of an iterative image reconstruction algorithm for electrical capacitance tomography[J]. Measurement Science and Technology, 1999, 10(7):37–39. DOI:10.1088/0957-0233/10/7/102 |
 2017, Vol. 34
2017, Vol. 34 


