高温下除尘过程普遍存在于工业生产中,例如整体煤气化联合循环 (IGCC) 和增压流化床燃烧联合循环 (PFBC) 过程。高温静电除尘器是满足上述气体净化要求的重要设备。对高温静电除尘过程的研究有助于揭示除尘机理,也能为工程实际中除尘设备的设计和优化提供指导。
国内外对常温下静电除尘器内部的荷电多相流在数值计算方面进行了比较深入的研究。学者们对电场和流场的耦合计算[1-4]、离子风的作用[5]、荷电过程[6-7]、细颗粒在耦合场中的分布[8],以及颗粒与颗粒、颗粒与壁面直接相互作用对粉尘层行为的影响[9]等方面进行了研究。Watanabe[6]和Meroth等[7]研究荷电颗粒在气流中的运动,但忽略了颗粒电场荷电对电势和离子荷电密度分布的影响。Cristina和Feliziani[10]考虑电场荷电对计算的影响,并采用饱和荷电量作为颗粒的荷电量,但是由于颗粒是在流经电场时不断荷电的,饱和电量只是颗粒荷电量的粗略估计。Li等[11]考虑温度对平板静电除尘的影响,研究温度对静电除尘器内流场特性、电场特性以及离子风效应的影响。然而,对于静电除尘器的研究大部分都局限于常温下,在高温下颗粒的行为还不清楚。本文的主要工作是建立静电除尘过程的多场耦合模型,研究平板静电除尘器在293~1 273 K温度条件下的颗粒受力情况,分析颗粒行为特性。
1 数学模型关于本文中所采用的数学模型和算法已经在前期研究[11]中论述过,为保持论文的完整性,对其进行简单介绍。
1.1 气相控制方程对于气相运动,采用雷诺平均方法 (RANS)。对于稳态的湍流流动状态,其控制方程如下:
| $ \frac{\partial }{{\partial {x_k}}}\left( {\rho {u_k}} \right) = 0, $ | (1) |
| $ \begin{array}{*{20}{c}} {\frac{\partial }{{\partial {x_k}}}\left[ {\rho {u_i}{u_k} - \left( {\mu + {\mu _t}} \right)\frac{{\partial {u_i}}}{{\partial {x_k}}}} \right] = - \frac{{\partial P}}{{\partial {x_i}}} + } \\ {{f_{Di}} + \left( {{\rho _{{\text{ion}}}} + {\rho _{{\text{pc}}}}} \right){E_i},} \end{array} $ | (2) |
| $ \frac{\partial }{{\partial {x_k}}}\left( {\rho {u_k}{C_{\text{p}}}T} \right) = \frac{\partial }{{\partial {x_k}}}\left( {{\lambda _t}\frac{{\partial T}}{{\partial {x_k}}}} \right) + {q_{\text{V}}}, $ | (3) |
其中:fDi是单位体积的曳力;ρion, ρpc分别是离子电荷密度和颗粒电荷密度;Ei是电场强度分量;P和T分别为流体的压力和温度;cp为流体的比热容;λt是流体导热系数;qV表示由颗粒引起的体积热源。
1.2 电场控制方程在线板式静电除尘器中,电场和离子荷电密度由泊松方程和电流连续性方程描述。
| $ \frac{{{\partial ^2}\varphi }}{{\partial x_k^2}} = - \frac{{{\rho _{{\text{ion}}}} + {\rho _{{\text{pc}}}}}}{{{\varepsilon _0}}}, $ | (4) |
| $ \frac{{\partial \varphi }}{{\partial {x_k}}}\left[ {{\rho _{{\text{ion}}}}\left( {{k_{{\text{ion}}}}{E_k} + {u_k}} \right) - {D_{\text{e}}}\frac{{\partial {\rho _{{\text{ion}}}}}}{{\partial {x_k}}}} \right] = 0, $ | (5) |
其中:φ为电势;ε0为真空介电常数;kion为离子迁移率;Ek为场强在xk方向上的分量;De为离子的有效扩散系数;δ为与标况下相比的相对密度T0=273.15 K, P0=101 325 Pa。
1.3 颗粒荷电控制方程在静电除尘器内某一点发生电场荷电需要满足一定的条件,电场荷电只发生在当前荷电量qp小于饱和荷电量qs时,饱和荷电量计算:
| $ {q_{\text{s}}} = 3\frac{{{\varepsilon _{\text{r}}}}}{{{\varepsilon _{\text{r}}} + 2}}{{\rm{\pi }}}{\varepsilon _0}d_{\text{p}}^2E, $ | (6) |
其中:ε0为真空介电常数;ε0=8.854×10-12 C/(v·m);εr为电介质 (烟气) 的相对介电常数;dp为颗粒直径。
颗粒电场荷电量随时间变化的关系式为
| $ {q_t} = {q_{\text{s}}}\frac{1}{{1 + \frac{\tau }{t}}}, $ | (7) |
其中:t为时间,τ为粒子荷电的时间常数 (达到饱和荷电量一半时所用的时间)。
扩散荷电随时间的变化关系式用下式近似计算:
| $ q = \frac{{2{{\rm{\pi }}}{\varepsilon _0}{d_{\text{p}}}{k_{\text{B}}}T}}{e}\ln \left( {\frac{{{d_{\text{p}}}{\rho _{{\text{ion}}}}e\bar V}}{{8{\varepsilon _0}{k_{\text{B}}}T}}t + 1} \right), $ | (8) |
其中:kB为Boltzmann常数,kB=1.38×10-23 J/K;e为基本电荷,e=1.6×10-19 C;V为离子的均方根速度。
1.4 固相控制方程本文采用拉格朗日法追踪颗粒。在气固两相流中,颗粒与流体进行着强烈的动量交换。在流体中运动颗粒受到的作用力通常包括:曳力、重力、浮力、Saffman升力、热泳力、压力梯度力和虚拟质量力等,如表 1所示。静电除尘器内的颗粒还受到电场力的作用。详细的颗粒控制方程请参考文献[11]。
|
|
表 1 颗粒受力计算公式列表 Table 1 Calculation formula of the force acting on the particle |
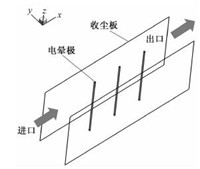
根据上述数学模型,本文基于计算流体力学FLUENT软件开发了适用于高温静电除尘器多物理耦合过程的三维数值模拟平台。本文研究的静电除尘器三维几何区域结构如图 1所示。电除尘设备在长宽高方向上的尺寸分别为0.5 m×0.12 m×0.24 m,具有3个直径为5 mm的电晕极,线间距为0.1 m,线板距 (异极距) 为0.06 m。由于设备装置结构的对称性,本文只研究静电除尘器结构的一半以减少计算量。
|
Download:
|
|
图 1 3-D静电除尘器计算几何区域示意图 Fig. 1 Schematic of precipitator geometry model |
|
入口气体质量流率为0.034 7 kg/s (相当于293 K时1.0 m/s, Re=8 840),喷入的粉尘粒子假设为球形,粒径为2.5 μm,密度为2 500 kg/m3,相对介电常数为4.0。颗粒以与气体相同的速度从入口进入,颗粒质量浓度为2 g/m3。运行电压取79 192 V,温度是293 K (20 ℃)。把上述工况作为基础工况,考虑4种有限体积网格数:412 320,654 610,824 640,1 236 960,不同网格数的模型均对0.1 μm颗粒 (其他条件同基本工况) 在静电除尘器中的运动进行模拟计算,得到相应的除尘效率分别为77.4%,82.5%,82.7%和82.4%。由此可见,当网格数由654 610增加到1 236 960时,除尘效率的变化微小,即认为此时网格对模拟结果的影响很小,因此确定用于空间离散的网格节点数为654 610个。
2.2 边界条件本文对三维静电除尘器内的颗粒的行为进行研究。主要从颗粒的荷电和受力来分析颗粒运动轨迹以及静电除尘器的除尘效率。工况参数列示见表 2。
|
|
表 2 温度对颗粒行为影响的模拟工况参数设置 Table 2 Simulation parameters for temperature effect on particle behavior |
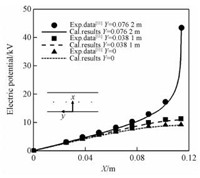
为了验证本文数值模型的准确性,将模拟结果与Penny和Matick[12]的经典实验数据进行对比。实验装置采用的是0.3 mm的电晕线,线板距0.114 3 m,线间距0.152 4 m,运行电压43.5 kV。图 2给出计算得到的沿X方向对应不同Y值时的电势分布。显然模拟的结果与实验数据吻合地很好。本文的模型能对电场进行很好的预测。
|
Download:
|
|
图 2 静电除尘器内电势特性曲线的模拟结果与Penny和Matick的实验数据的对比图 Fig. 2 Comparison of electric potential characteristic curves between computational results and experimental data in the ESP |
|
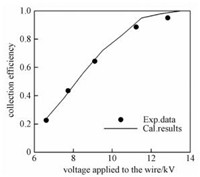
捕集效率的验证与Kihm等[13]的实验数据进行对比。实验设备是八线-线板式静电除尘器,电晕线直径为0.1 mm,喷入的油酸液滴的粒径为4 μm。由图 3可以看出,模拟的结果与实验吻合得很好。
|
Download:
|
|
图 3 除尘效率的模拟结果与Kihm的实验数据对比图 Fig. 3 Comparison of collection efficiencies between computational results and experimental data of Kihm |
|
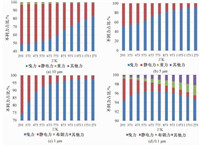
图 4给出4种粒径颗粒在不同温度下的受力相对大小,及颗粒主要的3种受力的相对占比,从下到上依次表示:曳力、电场力、第3种主要受力 (重力或布朗力) 以及其他力之和。从图 4可以看出曳力、静电力是颗粒的主要受力。其次,随着温度的升高,曳力占颗粒总受力的比例增加。即温度越高,流体对颗粒的运动的曳力作用越显著。对10 μm的颗粒,曳力和电场力比其他力大得多,主导颗粒的运动。随着温度的升高,重力所占比值减小,从293 K的2.4%到1 273 K的0.5%。浮力、布朗力、Saffman升力、热泳力、压力梯度力和虚拟质量力比重力小得多,在符合精度要求的条件下这些力可以忽略。其中,Saffman升力随着温度的升高,比例增大,对运动的影响增加,在1 073 K时与重力达到同一数量级。Saffman升力和布朗力在293~1 273 K的研究区间内随着温度的升高,增加一个数量级。而电场力随着颗粒荷电量和场强二者的减小而减小,同时,曳力因为气体黏度的增大而增大。
|
Download:
|
|
图 4 不同粒径颗粒在不同温度下的受力相对大小 Fig. 4 Relative sizes of particle force at different temperatures at different particle diameters |
|
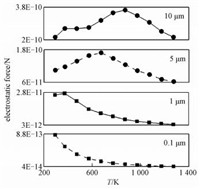
由于电场力和曳力对颗粒的运动过程起着重要作用,下面将分别研究二者随温度的变化规律。图 5给出不同温度下不同粒径颗粒平均的电场力。从图中可以看出,细颗粒的静电力明显小于粗颗粒,且粒径不同,其变化趋势也不一样。对于粗颗粒 (10 μm和5 μm),静电力随着温度的升高先升高后降低;对于细颗粒 (1 μm和0.1 μm),静电力随着温度的升高单调递减 (除开头微增)。静电力主要受颗粒荷电量和场强的影响,其中颗粒荷电量与离子电荷密度、荷电时间有关。
|
Download:
|
|
图 5 颗粒不同温度下平均电场力大小 Fig. 5 Variation in Coulomb force acting on the particle with temperature |
|
场强和离子电荷密度都是随温度的增加而减小,因此,图 5现象的主要原因是荷电时间随温度的变化的不同。粗颗粒在很短的时间内到达收尘板,荷电时间较短。高温使颗粒在整个静电除尘器内的运动时间缩短,荷电时间不确定。对于很早就能被捕集的颗粒来说,高速致使其被捕集推后,这样荷电时间延长;对于从出口逃逸走的颗粒来说,高温 (高速) 意味着荷电时间缩短。这就导致高温对不同粒径颗粒静电力变化趋势的影响也不同。
对于粗颗粒 (10 μm和5 μm) 而言,由于高温延长荷电时间,同时场强和离子电荷密度都随温度的增加而减小,静电力表现为先增大后减小。对于细颗粒 (1 μm和0.1 μm) 而言,高温 (高速) 缩短其荷电时间,同时场强和离子电荷密度都随着温度的增加而减小,静电力随着温度的升高而减小。以上不同粒径颗粒静电力的不同变化规律是由于高温的这两种影响机制共同决定的。
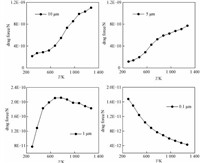
3.3 温度影响颗粒所受的曳力平均值曳力是由于气固两相的速度差造成的作用项,速度高的一方会对速度低的一方产生拖曳作用,反过来,速度低的一方会阻碍速度高的一方。温度的变化对曳力影响很显著,图 6给出4种不同粒径颗粒的曳力随温度的变化趋势。
不同粒径颗粒的曳力随温度变化规律不同,对于粒径为10 μm和5 μm的颗粒,随着温度的升高,曳力增加;对于粒径为1 μm颗粒,随着温度的升高,曳力先增加后减小;对于粒径为0.1 μm的颗粒,随着温度的升高,曳力减小。上述曳力大小随温度不同的演变规律是与曳力相关的参数随温度变化的综合作用的结果。
|
Download:
|
|
图 6 不同粒径颗粒的曳力随温度变化图 Fig. 6 Variation in drag force acting on the particles of different diameters with temperature |
|
曳力=颗粒质量×曳力系数×相对速度,
| $ {\mathit{\boldsymbol{F}}_{\rm{D}}} = {m_{\rm{p}}}{F_{\rm{D}}}\left( {\mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{u}}_{\rm{p}}}} \right),{\mathit{\boldsymbol{F}}_{\rm{D}}} = \frac{{18\mu }}{{d_{\rm{p}}^2{\rho _{\rm{p}}}{C_{\rm{c}}}}}. $ | (9) |
对于特定粒径的颗粒,曳力与曳力系数和相对速度大小有关。曳力系数采用的是考虑小颗粒Cunningham修正的曳力系数,其与气体的黏度和颗粒的粒径、密度以及Cunningham修正系数有关。随着温度的升高,气体黏度和Cunningham修正系数均增大,如图 7所示。曳力系数的变化取决于二者的相对增加幅度。其中,Cunningham修正系数本身是为修正小颗粒的曳力而引入的系数。从图中也可以看出,小颗粒 (小于1 μm) 的Cunningham修正系数随温度的变化不能忽略。

|
Download:
|
|
图 7 不同粒径颗粒的Cunningham修正系数随温度变化图 Fig. 7 Variation in Cunningham correction coefficient at different particle diameters with temperature |
|
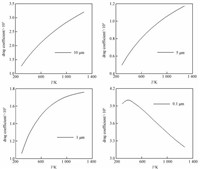
从物理意义上讲,之所以对小颗粒进行曳力修正是因为当颗粒很小,以至于同空气分子的尺寸可以相比较时,气体的连续性假设 (斯托克斯定律假设气体为连续性介质) 就不成立了。所以对曳力加一个修正系数,也称滑脱修正系数。由图 5也可以看出,对于5 μm以上的颗粒Cc大约为1,而对于1 μm以下的颗粒,其修正是必要的。Cunningham修正系数对不同粒径的敏感度不同,或者说是粒径由大变小的过程中曳力变化从量变到质变从而导致不同粒径的不同曳力变化规律。不同粒径颗粒的曳力系数随温度的变化具体如图 8所示。
|
Download:
|
|
图 8 不同粒径颗粒的曳力系数随温度变化图 Fig. 8 Variation in drag coefficient at different particle diameters with temperature |
|
从图 4~图 6中可以看出电场力和曳力的大小在常温下相差不大,但是随着温度的升高,电场力明显小于曳力,其随温度变化的幅值也小于曳力变化幅值,即曳力随温度的增加速率比静电力变化快,这可能是导致高温下除尘效率降低的原因。
4 结论本文对线板式静电除尘器内温度对颗粒荷电、受力的影响进行研究,最后分析除尘效率降低的影响。基于本文的研究结果,得到以下结论:
1) 随着温度的升高,静电力减小而Saffman升力、布朗力以及曳力均增大。对于10 μm的颗粒,颗粒受到的力主要是静电力和曳力。对于微米及微米级以上的颗粒,重力不能忽略。对于亚微米颗粒,布朗扩散效应对颗粒的运动有着重要的影响,不能忽略。小颗粒和大颗粒在静电场中的受力不同,运动规律不同,一些适用于大颗粒的规律并不适用于小颗粒。曳力随温度的增加速率比静电力变化快。
2) 随着温度的升高,电场力明显小于曳力,其随温度变化的幅值也小于曳力变化幅值,即曳力随温度的增加速率比静电力变化快,这可能是导致高温下除尘效率降低的原因。
| [1] | Lami E, Mattachini F, Gallimberti R, et al. A numerical procedure for computing the voltage-current characteristics in electrostatic precipitator configurations[J]. Journal of Electrostatics, 1995, 34(4):385–399. DOI:10.1016/0304-3886(94)00030-Z |
| [2] | Neimarlija N, Demirdzic I, Muzaferija S. Finite volume method for calculation of electrostatic fields in electrostatic precipitators[J]. Journal of Electrostatics, 2009, 67(1):37–47. DOI:10.1016/j.elstat.2008.10.007 |
| [3] | Schmid H J, Vogel L. On the modelling of the particle dynamics in electro-hydrodynamic flow-fields:I. Comparison of Eulerian and Lagrangian modelling approach[J]. Powder Technology, 2003, 135:118–135. |
| [4] | Schmid H J. On the modelling of the particle dynamics in electro-hydrodynamic flow fields:Ⅱ. Influences of inhomogeneities on electrostatic precipitation[J]. Powder Technology, 2003, 135:136–149. |
| [5] | Kallio G A, Stock D E. Interaction of electrostatic and fluid dynamic fields in wire plate electrostatic precipitators[J]. Journal of Fluid Mechanics, 1992, 240:133–166. DOI:10.1017/S0022112092000053 |
| [6] | Watanabe T. Calculation of flyash particle motion and its migration velocity in an electrostatic precipitator[C]//Industry Applications Society Annual Meeting. Conference Record of 1989 IEEE, 1989:2126-2136. |
| [7] | Meroth A M, Rastogi A K, Schwab A J. Numerical computation of the turbulent particulated flow in an electrostatic precipitator[C]//International Symposium on Filtration and Separation of Fine Dust. 1996. |
| [8] | Adamiak K, Atten P. Numerical simulation of the 2-D gas flow modified by the action of charged fine particles in a single-wire ESP[J]. IEEE Transactions on Dielectrics And Electrical Insulation, 2009, 16(3):608–614. DOI:10.1109/TDEI.2009.5128495 |
| [9] | Guo B, Yang S Y, Xing M, et al. Toward the Development of an Integrated Multiscale Model for Electrostatic Precipitation[J]. Industrial & Engineering Chemistry Research, 2013, 52(33):11282–11293. |
| [10] | Cristina S, Feliziani M. Caculation of ionized fields in DC electrostatic precipitators in the presence of dust and electric wind[J]. ZEEE Transactions on Industry Applications, 1995, 31(5):1446–1451. |
| [11] | Li Y, Zheng C, Luo K, et al. CFD simulation of high-temperature effect on EHD characteristics in a wire-plate electrostatic precipitator[J]. Chinese Journal of Chemical Engineering, 2015, 23:633–640. DOI:10.1016/j.cjche.2014.06.038 |
| [12] | Penney G W, Matick R E. Potentials in D-C corona fields[J]. Transactions of American Institute of Electrical Engineers, 1960, 79:91–99. |
| [13] | Kihm K D, Mitchner M, Self S A. Comparison of wire-plate and plate-plate electrostatic precipitators in turbulent flow[J]. Journal of Electrostatics, 1987, 19(1):21–32. DOI:10.1016/0304-3886(87)90013-1 |
 2017, Vol. 34
2017, Vol. 34 


