闪蒸是指当过热液体暴露在低于自身温度下饱和压力的空间时,骤然蒸发并且自身温度迅速下降的现象。根据液膜是否具有水平速度,闪蒸可以分为静态闪蒸和循环闪蒸。闪现象是一个包含有动量、质量和能量传递的复杂的多相流动与传热过程,过程中伴有汽泡的成核、生长、聚集、破裂和汽液界面的剧烈波动,以及晶体析出等多种物理现象。闪蒸由于具有较高的分离效果和传热能力,被广泛应用于海水淡化、地热电站、盐化工以及药品的干燥与消毒等领域。
1973年,Miyatake等[1]对静态闪蒸进行实验研究,结果表明过热度是促使闪蒸发生的原动力。他们将闪蒸过程分为快速蒸发和缓慢蒸发两个阶段,并定义闪蒸时间、不平衡分数、不平衡温差等基本概念,给出相应的实验关联式。实验结果表明液膜的最大沸腾厚度、不平衡温差,以及闪蒸蒸发量等都受到初始温度和初始液膜厚度影响。1992年,Gopalakrishna和Lior[2]对纯水以及浓度为0~0.035的NaCl溶液进行闪蒸实验研究。其液膜初始温度为25~80 ℃,过热度为0.5~10 ℃,初始液位为165~467 mm。实验结果表明闪蒸蒸发量随着Jacob数的增大而增大,随Pr数的增大而减少,在此基础上得到闪蒸蒸发量的实验关联式。1996年,Kim和Lior[3]实验研究纯水的静态闪蒸,过热度为2~7 ℃, 液膜初始温度为40~80 ℃,在给定的液膜厚度下,闪蒸结束时的不平衡温差 (NETD) 随着初始水温的升高先减小后增大,静止液膜存在一个临界水温,当初始液膜低于这个临界水温时,NETD随着液膜厚度的减小而减小;反之NETD随着液膜厚度的减小而增大。2001年,Saury等[4]对初始液位为15 mm、初始温度为30~70 ℃、过热度为1~35 ℃的纯水闪蒸进行实验研究,指出过热度和初温是影响闪蒸的主要因素,根据热平衡给出闪蒸蒸发量和过热度之间的实验关联式,并提出利用闪蒸速度系数确定闪蒸持续时间的方法,其准确度较Miyatake提出的闪蒸时间计算式有很大的提高。Augusto等[5]对于具有自由液面的纯水闪蒸机理进行实验研究。Raj等[6]对闪蒸在海水淡化中的应用和闪蒸近年来的发展做了较为详细的综述。Shao等[7]研究较高压力、较高温度下的闪蒸现象,及不同初始条件对不平衡分数的影响。
本课题组对纯水和质量分数为0~0.26的NaCl溶液静态闪蒸传热特性进行实验研究[8],建立蒸汽携带效应的模型[9],研究静态闪蒸过程中的液膜蒸发特性[10]和闪蒸过程中单个汽泡的生长过程[11]。以往的研究主要集中在整个闪蒸过程的平均传热特性[12],较少涉及闪蒸过程中瞬态传热特性的研究。本文利用高速摄像机对闪蒸过程进行记录,结合不同初始条件下的闪蒸沸腾形态对瞬态传热特性进行比较分析。
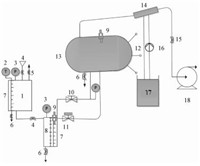
1 实验系统及不确定度分析静态闪蒸实验系统如图 1所示,电磁阀将实验系统分为高压侧和低压侧,高压侧主要包括加热器与闪蒸腔,低压侧主要有真空腔、真空泵与辅助冷凝循环。
|
Download:
|
|
1加热器,2温度表,3压力表,4注水阀,5排气阀,6疏水阀,7液位计,8闪蒸腔,9压力传感器,10调节阀,11电磁阀,12热电偶,13真空腔,14冷凝器,15真空阀,16循环水泵,17冷却水槽,18真空泵。 图 1 静态闪蒸实验系统图 Fig. 1 Static flash evaporation experimental system |
|
闪蒸腔是闪蒸发生的重要部件,其尺寸为0.20 m×0.20 m×0.61 m, 前后为可视化钢化玻璃其余壁面用石棉绒覆盖保温,闪蒸腔的顶部装有MSI-US5100压阻式压力传感器,在闪蒸腔的正中心轴线上安装19只热电偶,用来检测闪蒸腔内的汽水温度变化。实验时所使用的温度测量装置是精度为0.2 ℃的铜-铜镍热电偶,闪蒸腔和真空腔的压力传感器的测量精度为0.75%,测量范围是0~0.25 MPa。实验所采用的NaCl晶体纯度不小于99.5%,NaCl溶液浓度的测量采用精度为5×10-4 kg·m-3的24只精密比重计,记录闪蒸过程的高速摄像机的型号为Phantom v611。
本文使用Moffat[13]给出的方法对实验结果进行不确定度分析,表 1给出实验中所有参数的不确定度分析结果。
|
|
表 1 实验参数的不确定度 Table 1 Uncertainty analysis of experiment parameters |
瞬态传热系数表征闪蒸腔内瞬时换热强度。瞬态传热系数的大小与沸腾形态相对应,瞬态传热系数越大所对应的液膜湍动越剧烈;反之,液膜状态越平缓。
2.1 闪蒸过程中沸腾形态的变化在静态闪蒸过程中,液膜存在沸腾形态的变化,图 2为沸腾形态变化图。

|
Download:
|
|
图 2 沸腾形态图 Fig. 2 Boiling state diagram |
|
闪蒸开始时,液膜迅速过热,热量开始由显热转变为汽化潜热,形成汽泡;随着汽泡的长大、融合、堆积、破裂,液膜转变为泡沫状混合物;闪蒸后期由于液膜中不稳定能量的减少,汽泡只在液膜表面产生,液膜底部出现连续的液相。
从图 2可以看出,随着闪蒸的开始,液膜中的不稳定能量迅速转换为闪蒸蒸汽的潜热,液膜沸腾形态的剧烈变化实质在于闪蒸过程中较高的能量转化速率;引入瞬态传热系数并研究瞬态传热系数的变化规律可以较好地反映闪蒸过程的本质。
2.2 瞬态传热系数的定义瞬态传热系数定义为:单位时间内单位体积的液膜在单位过热度下的换热量。如式 (1) 所示。瞬态传热系数的单位为kW·m-3·℃-1。
| $ {h_s} = \frac{{\Delta {m_{{\text{ev}}}}r}}{{\Delta \tau A{H_0}\Delta T}} = \frac{{\Delta {M_{{\text{ev}}}}r}}{{\Delta \tau \Delta T}}, $ | (1) |
其中: ΔMev为单位体积液膜在Δτ 时间段内沸腾产生的蒸汽量,kg; ΔT 是液膜的过热度,℃;r是液膜的汽化潜热,kJ·kg-1。
| $ {M_{{\text{ev}}}} = \frac{{{\rho _1}{c_{{\text{pl}}}}\Delta T\left[ {1 - {\text{NEF}}\left( \tau \right)} \right]}}{r}, $ | (2) |
其中: Mev为单位体积液膜在τ 时间段内沸腾产生的蒸汽量,kg;NEF是液膜的不平衡分数;cpl是液膜的定压比热,kJ·kg-1·℃-1; ρl为溶液密度,kg·m-3。
| $ {\text{NEF}}\left( \tau \right) = \frac{{{T_{\text{w}}}\left( \tau \right) - {T_{{\text{se}}}}}}{{\Delta T}}, $ | (3) |
其中: Tw(τ) 为液膜在τ 时刻的温度,℃; Tse 为液膜在平衡时刻的温度,℃。
将 (2)、(3) 式代入到 (1) 式,可得到闪蒸过程中的瞬态传热系数为
| $ {h_s}\left( \tau \right) = - \frac{{{\rho _1}{c_{{\text{pl}}}}\Delta {\text{NEF}}\left( \tau \right)}}{{\Delta \tau }}. $ | (4) |
计算过程中工质的定性温度Twp取为闪蒸开始和平衡时刻的平均值,如下:
| $ {T_{{\text{wp}}}} = 0.5\left( {{T_{{\text{w}}0}} + {T_{{\text{se}}}}} \right). $ | (5) |
由式 (4) 可知,瞬态传热系数是时间的函数,同时对应着不同的沸腾形态。
2.3 瞬态传热系数的变化规律瞬态换热系数表征闪蒸过程中瞬时换热强度,是影响闪蒸沸腾形态变化的主要因素,瞬时换热系数达到峰值时,闪蒸腔内沸腾最为剧烈,液膜上下翻滚形成泡沫状混合物。整体而言,闪蒸过程的瞬态传热系数先增加,后减小,最后趋于零。根据闪蒸过程中液膜的状态和沸腾传热强度,将闪蒸分为前期和后期。前期是闪蒸开始到液膜最大范围沸腾 (瞬态传热系数到达最大) 之间,后期是液膜最大范围沸腾到液膜完全平息之间。
2.3.1 过热度对瞬态传热系数的影响在不同的过热度下,瞬态传热系数的变化规律如图 3所示。

|
Download:
|
|
图 3 过热度对瞬态传热系数的影响 Fig. 3 Influence of superheat on the instantaneous heat transfer coefficient |
|
由图 3可知:过热度对闪蒸瞬态传热系数的影响在不同的闪蒸阶段影响不同,在闪蒸进行的前期,过热度越大,闪蒸瞬态传热系数越小;在闪蒸过程后期的开始阶段,过热度越大闪蒸瞬态传热系数越大,在后期的末尾阶段,过热度的大小对闪蒸瞬态传热系数影响不大。
这是因为,在其他条件相同时,根据式 (1),过热度对瞬态传热系数的影响是通过闪蒸瞬态传热量和过热度的比值体现的。闪蒸瞬态传热量随着过热度的增大而增大,随着液膜沸腾范围的增大而增大。闪蒸瞬态传热量与过热度的比值随闪蒸沸腾范围改变而变化。
在闪蒸的前期,液膜产生汽泡少,液膜沸腾范围小,闪蒸瞬态传热量主要受沸腾范围影响。由瞬态传热系数的定义与式 (1) 可知,瞬态传热量在分子,过热度在分母,故在闪蒸进行的前期,过热度越大,瞬态传热系数越小。闪蒸过程到达后期时,闪蒸腔内液体达到最大范围沸腾,液膜产生大量的汽泡,闪蒸瞬态传热量较大,闪蒸瞬态传热量与过热度的比值随过热度的增大而增大,瞬态传热系数随过热度的增大而增大。在闪蒸过程的后期末尾阶段,闪蒸传热主要靠缓慢蒸发,过热度对瞬态传热系数影响较小。
2.3.2 初始液膜高度对瞬态传热系数的影响在不同的初始液膜高度下,瞬态传热系数的变化规律如图 4所示。

|
Download:
|
|
图 4 初始液膜高度对瞬态传热系数影响 Fig. 4 Influence of initial water film height on the instantaneous heat transfer coefficient |
|
由图 4可知:在液膜高度研究范围内,随初始液膜高度的增加,瞬态传热系数的最大值呈现减小趋势;瞬态传热系数随初始液膜高度的增加,最大值点出现时刻延迟。
这是因为在闪蒸过程中,随着初始液膜高度的增加,在相同的过热度下,液膜沸腾范围达到最大值所需时间增长。在闪蒸的前期,液膜内部的汽化潜热已经释放较多,到达闪蒸后期时,闪蒸瞬态传热量的最大值随着前期时间的增加而减小,故闪蒸瞬态传热系数的最大值呈减小趋势。闪蒸前期的时间增长,即到达闪蒸后期的时刻延后,所以瞬态传热系数出现峰值的时刻滞后。
2.3.3 初始液膜浓度对瞬态传热系数的影响在不同的初始液膜浓度下,瞬态传热系数的变化规律如图 5所示。

|
Download:
|
|
图 5 初始液膜浓度对瞬态传热系数影响 Fig. 5 Influence of initial water film concentration on the instantaneous heat transfer coefficient |
|
由图 5可知:在研究范围内,当初始液膜高度和初始过热度相同时,瞬态传热系数的峰值随着初始液膜浓度的增大而呈减小趋势,这是因为随着初始液膜浓度的增加,沸腾传热受到抑制。在研究范围内,初始液膜浓度对瞬态传热系数的峰值出现时刻影响不大。
2.3.4 瞬态传热系数实验关联式闪蒸过程中的瞬时传热系数可根据已有NEF实验关联式[8]推导计算。
| $ {\text{NEF}}\left( \tau \right) = {\text{erf}}\left[ {{{\left( {\frac{{{H_0}}}{2}\sqrt {\frac{{{\rho _1}{c_{{\text{pl}}}}}}{{\lambda \tau }}} } \right)}^{{a_2}}}} \right], $ | (6) |
其中: a2=0.340 0lnΔT+2.897 1,
对NEF (τ) 求导可得
| $ {\text{NEF'}}\left( \tau \right) = \frac{2}{{\sqrt {{\rm{\pi }}} }}\alpha \beta {{\text{e}}^{ - {\alpha ^2}{\tau ^{2\beta }}}}{\tau ^{\beta - 1}}, $ | (7) |
将式 (7) 代入式 (4) 得到
| $ {h_s}\left( \tau \right) = - \frac{2}{{\sqrt {{\rm{\pi }}} }}\alpha \beta {{\text{e}}^{ - {\alpha ^2}{\tau ^{2\beta }}}}{\tau ^{\beta - 1}}{\rho _1}{c_{{\text{pl}}}}, $ | (8) |
式中:
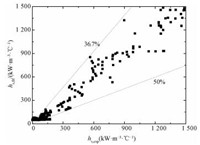
将瞬态传热系数的实验值和实验关联式计算值相对比,得到的结果如图 6所示。
|
Download:
|
|
图 6 瞬态传热系数关联式计算值和实验值的相对误差 Fig. 6 Relative errors between the calculated and experimental instantaneous heat transfer coefficients |
|
从图 6得知,80%左右的瞬态传热系数的实验值和关联式的计算值相对误差在50%以内,表明实验关联式具有一定的精度。实验值和关联式拟合值相差较大的是在瞬态传热系数较小区段。因为在瞬时换热系数较小时,实验测量误差较大,所以拟合值准确度比较差。总体看来,实验关联式计算结果与实验结果吻合良好。
3 结论本文对质量分数为0~0.26的NaCl溶液瞬态沸腾传热特性与沸腾形态变化进行实验研究。研究瞬态传热系数随闪蒸初始条件的变化规律;得到闪蒸过程中的沸腾状态与瞬态传热系数的对应关系和以下结论:
1) 在研究范围内,闪蒸前期瞬态传热系数随着过热度的增大而减小;闪蒸后期开始阶段,瞬态传热系数随着过热度的增大而增大;闪蒸后期末尾阶段,过热度对瞬态传热系数影响较小。
2) 在研究范围内,随着初始液膜高度的增加,瞬态传热系数峰值呈减小趋势,瞬态传热系数的峰值出现时刻延后。
3) 在研究范围内,随着初始液膜浓度的增加,瞬态传热系数峰值呈减小趋势,瞬态传热系数的峰值出现时刻几乎不受影响。
4) 在实验范围内,由瞬态传热系数的实验关联式得到的计算值与实验值吻合较好。
|
|
附表 1 变量符号说明 TableS1 Variable symbols' illustration |
| [1] | Miyatake O, Murakami K, Kawata Y, et al. Fundamental experiments with flash evaporation[J]. Heat Transfer-Japanese Research, 1973, 2(4):89–100. |
| [2] | Gopalakrishna S, Lior N. Analysis of bubble translation during transient flash evaporation[J]. International Journal of Heat and Mass Transfer, 1992, 35(7):1753–1761. DOI:10.1016/0017-9310(92)90145-I |
| [3] | Kim J, Lior N. Some critical transitions in pool flash evaporation[J]. International Journal of Heat and Mass Transfer, 1997, 40(10):2363–2372. DOI:10.1016/S0017-9310(96)00296-7 |
| [4] | Saury D, Harmand S, Siroux M. Flash evaporation from a water pool:influence of the liquid height and of the depressurization rate[J]. International Journal of Thermal Sciences, 2005, 44(10):953–965. DOI:10.1016/j.ijthermalsci.2005.03.005 |
| [5] | Augusto C M, Ribeiro J B, Gaspar A R, et al. Low-pressure-vaporization of free water-Characterization of the boiling regimes[J]. International Journal of Thermal Sciences, 2014, 77:19–26. DOI:10.1016/j.ijthermalsci.2013.10.006 |
| [6] | Raj M M A, Murugavel K K, Rajaseenivasan T, et al. A review on flash evaporation desalination[J]. Desalination and Water Treatment, 2016, 57(29):13462–13471. DOI:10.1080/19443994.2015.1070283 |
| [7] | Shao Y X, Li Y J, Yang L B, et al. New experimental system for high pressure and high temperature flashing evaporation experiments[J]. Applied Thermal Engineering, 2014, 66(1/2):148–155. |
| [8] | Zhang D, Chong D T, Yan J J, et al. Experimental study on static flash evaporation of aqueous NaCl solution at different flash speed:heat transfer characteristics[J]. International Journal of Heat and Mass Transfer, 2013, 65(7):584–591. |
| [9] | Zhang D, Chong D T, Yan J J, et al. Study on steam-carrying effect in static flash evaporation[J]. International Journal of Heat and Mass Transfer, 2012, 55(17/18):4487–4497. |
| [10] | 杨庆忠, 刘光耀, 张丹, 等. NaCl溶液静态闪蒸的蒸发特性[J]. 化工学报, 2013, 64(11):4068–4073. |
| [11] | 于龙文, 张丹, 赵凯, 等. 静态闪蒸过程中的单个汽泡成长实验研究[J]. 工程热物理学报, 2015, 36(6):1274–1277. |
| [12] | Zhang D, Chong D T, Yan J J, et al. Experimental study on static flash evaporation of aqueous NaCl solution[J]. International Journal of Heat and Mass Transfer, 2012, 55(23/24):7199–7206. |
| [13] | Moffat R J. Contributions to the Theory of Single-Sample Uncertainty Analysis[J]. Journal of Fluid Engineering-Transactions of the ASME, 1982, 104(2):250–260. DOI:10.1115/1.3241818 |
 2017, Vol. 34
2017, Vol. 34 


