螺旋环状流是垂直管内的一种重要流型，广泛存在于石油、化工与核能等工业领域。例如，传统的气液分离系统^[1-4]、气液强化换热系统^[5-9]以及非常规油气田的开发利用^[10]等。螺旋环状流中，中心高速螺旋气流与管壁螺旋液膜存在相对运动，由于不稳定性扰动的影响，引起气液各相流动结构和状态改变，导致液膜表面出现波动并发展成波动的液膜流动。深入了解液膜流动的水动力特性及其稳定性，研究其失稳过程、机理和控制条件是两相旋流技术应用推广的关键。

螺旋涡流作用下环状流的稳定性，其核心问题是管壁螺旋液膜与高速螺旋气流之间界面波的稳定性。与传统环状流不同，螺旋环状流中，两相螺旋流场诱导附加离心力作用于相界面，改变界面力平衡条件及相间作用机理，其特殊性将对界面波的动力学特性产生重要影响。

本文基于Kelvin-Helmholtz不稳定性理论，利用双流体模型，考虑旋流的影响，通过分析气液各相作用于相界面的受力平衡，建立螺旋涡流作用下环状流中界面波的动力学模型；采用特征根分析方法，获得界面失稳的临界条件，提出稳定性判断准则；基于此准则条件，系统分析气流速度、旋流强度及管径对液膜流动稳定性的影响规律。

1 数理模型

如图 1所示，管壁液膜在中心高速螺旋气流作用下沿竖直管道向上螺旋流动。圆管半径为R_o，液膜厚度平均值为δ。θ为螺旋流动方向与轴向的夹角，反映旋流强度的影响。理论分析时，作以下基本假设：

1) 液膜厚度与管径相比足够小，$ \bar \delta /{R_{\rm{o}}} \ll 1$;

2) 流体为稳态、无黏、不可压缩流动；

3) 气液流场充分发展，忽略速度耗散。

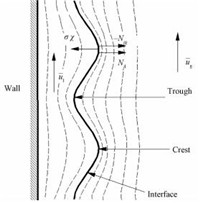
1.1 界面的扰动

根据图 2所示界面波结构示意图，假设气液两相为均匀无黏流动，界面波斜率足够小，相界面存在一个小扰动ŷ，则界面波方程^[11]可表示为

$ y = \hat y\cos k\left( {s - ct} \right), $

(1)

其中：y、ŷ、k、c、s分别为界面波波幅、波幅扰动量、波数 (k=2π/λ)、波速和界面波传播方向。

通常，波速c可以表示成复数的形式，即c=c_R+ic_I，因此，界面方程又可表示为

$ y = \hat y\cos k\left( {s - {c_{\text{R}}}t} \right){{\text{e}}^{k{c_{\text{I}}}t}}. $

(2)

波速虚部c_I与波数k的乘积β_I=kc_I定义为界面波的扰动增长率，用于确定特定流动条件下界面波的稳定性。当满足：

β_I>0时，界面波波幅随时间呈指数增大，扰动增加，流动处于不稳定状态；

β_I < 0时，界面波波幅随时间呈指数减小，扰动衰减，流动为稳定状态；

β_I=0时，界面波波幅保持不变，扰动稳定不变，为中性稳定条件。

因此，界面波的稳定性问题决定于流体的流动参数及物性参数，对于给定的波数k，通过计算波速虚部正负以判断流动的稳定性。

1.2 不稳定性分析 1.2.1 气相场

对于螺旋环状流中的气相场，首先，将三维螺旋运动分解为2个分运动：柱坐标系下的环状流叠加极坐标系下的圆周运动。在环状流分析基础上，得到气相场作用于相界面的正应力；然后，将圆周运动诱导产生的离心力作为附加正应力叠加到环状流分析结果上；最终得到螺旋环状流中气相场作用于相界面的总正应力大小。

1) 环状流

假设气相场为轴对称不可压缩流动，忽略气流黏性的影响及在管内的速度耗散，圆柱坐标系下的气相控制方程^[11]可以简化为

$ \begin{array}{*{20}{c}} {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r{u_r}} \right) + \frac{{\partial {u_z}}}{{\partial z}} = 0,} \\ {{u_r}\frac{{\partial {u_r}}}{{\partial r}} + {u_z}\frac{{\partial {u_r}}}{{\partial z}} = - \frac{1}{{{\rho _{\rm{g}}}}}\frac{{\partial p}}{{\partial r}},} \\ {{u_r}\frac{{\partial {u_z}}}{{\partial r}} + {u_z}\frac{{\partial {u_z}}}{{\partial z}} = - \frac{1}{{{\rho _{\rm{g}}}}}\frac{{\partial p}}{{\partial z}}.} \end{array} $

(3)

由于气液界面的扰动是由界面附近气相场的速度u及压强p波动引起的，引入速度流函数ψ，则扰动产生后的流函数和压强可以分别表示成：

$ \begin{gathered} \psi = \bar \psi \left( r \right) + \hat \psi \left( r \right){{\text{e}}^{{\text{i}}kz}}, \hfill \\ p = \bar p\left( z \right) + \hat p\left( r \right){{\text{e}}^{{\text{i}}kz}}. \hfill \\ \end{gathered} $

(4)

其中：ψ、p、$ {\hat \psi } $和$ {\hat p} $分别为稳态条件下的流函数和压强，以及流函数和压强的扰动值；k为轴向波数。

因此，轴向速度u_z和径向速度u_r可分别表示为

$ {u_z} = \frac{1}{r}\frac{{\partial \psi }}{{\partial r}},{u_r} = - \frac{1}{r}\frac{{\partial \psi }}{{\partial z}}. $

(5)

将式 (4)、式 (5) 代入式 (3)，消去稳态项并忽略二阶扰动量，得到扰动的控制方程：

$ {{\bar u}_z}\frac{{D\hat \psi }}{r} - D{{\bar u}_z}\frac{{\hat \psi }}{r} = - \frac{{\hat p}}{{{\rho _{\text{g}}}}}, $

(6)

$ {k^2}{{\bar u}_z}\frac{{\hat \psi }}{r} = - \frac{{D\hat p}}{{{\rho _{\text{g}}}}}. $

(7)

其中，D=∂/∂r。

对式 (6) 求偏导后联立式 (7) 消去压力扰动项，得到柱坐标系下的Orr-Sommerfeld方程

$ \begin{array}{*{20}{c}} {\left( {{{\bar u}_z} - {c_z}} \right)\left( {{D^2}\hat \psi - \frac{{D\hat \psi }}{r} - {k^2}\hat \psi } \right) + } \\ {\left( {\frac{{\partial {u_z}}}{{\partial r}} - {D^2}{u_z}} \right)\hat \psi = 0.} \end{array} $

(8)

其中，u_z－c_z为气相轴向平均速度与界面轴向波速之差。

当气相轴向平均速度u_z趋近于界面波速c_z时，上述方程中的第2项决定了临界层的影响^[11-12]。在K-H不稳定分析中，认为气相场平均轴向速度u_z在运动过程中基本保持不变，因此可以得到关于流函数ψ的微分方程

$ {D^2}\hat \psi - \frac{{D\hat \psi }}{r} - {k^2}\hat \psi = 0. $

(9)

式 (9) 为修正的贝塞尔微分方程，其通解可表示为

$ \hat \psi = Ar{I_1}\left( {kr} \right) + Br{{\text{K}}_1}\left( {kr} \right), $

(10)

其中：I₁和K₁分别为修正的一阶第一类、第二类贝塞尔函数；系数A、B由以下边界条件确定。

根据式 (5)、式 (10)，径向速度分量可表示为

$ {u_r} = - {\text{i}}k\left[ {A{{\text{I}}_1}\left( {kr} \right) + B{{\text{K}}_1}\left( {kr} \right)} \right]{{\text{e}}^{{\text{i}}kz}}. $

(11)

流动轴对称分布条件下，轴线处u_r=0，常数B等于0，则上式可简化为

$ {u_r} = - {\text{i}}kA{{\text{I}}_1}\left( {kr} \right){{\text{e}}^{{\text{i}}kz}}. $

(12)

通过界面处的径向速度边界条件确定另一个积分常数A。无黏性条件下，气流与界面波的相对速度u_z －c_z在整个气相场相等，且在气液界面处也等于

$ {u_r} = \left( {{{\bar u}_z} - {c_z}} \right)\frac{{\partial {r_i}}}{{\partial z}} = {\text{i}}k\hat \delta \left( {{{\bar u}_z} - {c_z}} \right){{\text{e}}^{{\text{i}}kz}}, $

(13)

式中，相界面的径向位置r_i可表示为

$ {r_i} = \left( {{R_{\text{o}}} - \bar \delta } \right) + \hat \delta {{\text{e}}^{{\text{i}}kz}}, $

(14)

其中，δ、$ {\hat \delta } $分别为液膜平均厚度及液膜厚度扰动量。

由式 (12)、式 (13) 得到常数$ A =-\hat \delta ({\bar u_z}-{c_z})/{I_1}(k{\bar r_i}) $，因此，流函数的扰动量$ {\hat \psi } $可表示为

$ \hat \psi \left( r \right) = - \hat \delta \left( {{{\bar u}_z} - {c_z}} \right)\frac{{r{{\text{I}}_1}\left( {kr} \right)}}{{{{\text{I}}_1}\left( {k{{\bar r}_i}} \right)}}. $

(15)

将式 (15) 代入动量方程式 (7)，积分得到环状流中气相场作用于相界面r=r_i的正应力扰动量

$ {\left( {{{\hat N}_{ig}}} \right)_1} = - k\hat \delta {\rho _{\text{g}}}{\left( {{{\bar u}_z} - {c_z}} \right)^2}. $

(16)

2) 圆周运动

忽略气相黏性的影响及在管内的速度耗散，极坐标系下气相圆周运动的控制方程^[13]可以表示为：

$ \begin{gathered} \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r{u_r}} \right) + \frac{1}{r}\frac{{\partial {u_\theta }}}{{\partial \theta }} = 0, \hfill \\ {u_r}\frac{{\partial {u_r}}}{{\partial r}} + \frac{{{u_\theta }}}{r}\frac{{\partial {u_r}}}{{\partial \theta }} - \frac{{u_\theta ^2}}{r} = - \frac{1}{{{\rho _{\text{g}}}}}\frac{{\partial p}}{{\partial r}}, \hfill \\ {u_r}\frac{{\partial {u_\theta }}}{{\partial r}} + \frac{{{u_\theta }}}{r}\frac{{\partial {u_\theta }}}{{\partial \theta }} + \frac{{{u_r}{u_\theta }}}{r} = - \frac{1}{{{\rho _{\text{g}}}}}\frac{{\partial p}}{{r\partial \theta }}. \hfill \\ \end{gathered} $

(17)

同理，引入流函数ψ，则扰动产生后的流函数和压强可分别表示成：

$ \begin{gathered} \psi = \bar \psi \left( r \right) + \hat \psi \left( r \right){{\text{e}}^{{\text{i}}m\theta }}, \hfill \\ p = \bar p\left( \theta \right) + \hat p\left( r \right){{\text{e}}^{{\text{i}}m\theta }}. \hfill \\ \end{gathered} $

(18)

其中，m为周向波数。

周向速度u_θ及径向速度u_r可分别表示为

$ {u_r} = \frac{1}{r}\frac{{\partial \psi }}{{\partial \theta }},{u_\theta } = - \frac{{\partial \psi }}{{\partial r}}. $

(19)

类似于环状流的分析，圆周运动中气流作用于相界面的正应力扰动量$ {({{\hat N}_{i{\rm{g}}}})_2} $为

$ {\left( {{{\hat N}_{ig}}} \right)_2} = - \left[ {{\rho _{\text{g}}}\hat \delta m\frac{{{{\left( {{{\bar u}_\theta } - {c_\theta }} \right)}^2}}}{{{{\bar r}_i}}} + {\rho _{\text{g}}}\hat \delta \frac{{\bar u_\theta ^2}}{{{{\bar r}_i}}}} \right]. $

(20)

气液界面沿轴向无限发展，沿周向周期性变化。假设环状流、圆周运动两分运动条件下界面波波长大小数量级相同，则轴向波数k与周向波数m满足关系k=m/r_i，式 (20) 又可表示为

$ {\left( {{{\hat N}_{ig}}} \right)_2} = - \left[ {{\rho _{\text{g}}}\hat \delta k{{\left( {{{\bar u}_\theta } - {c_\theta }} \right)}^2} + {\rho _{\text{g}}}\hat \delta \frac{{\bar u_\theta ^2}}{{{{\bar r}_i}}}} \right]. $

(21)

因此，螺旋环状流中气相场作用于相界面的总正应力扰动量为

$ \begin{gathered} {{\hat N}_{ig}} = {\left( {{{\hat N}_{ig}}} \right)_1} + {\left( {{{\hat N}_{ig}}} \right)_2} \hfill \\ \;\;\;\;\;\; = - {\rho _{\text{g}}}k\hat \delta {\left( {{{\bar u}_\theta } - {c_\theta }} \right)^2} - \frac{{{\rho _{\text{g}}}\hat \delta {{\left( {\sin \theta } \right)}^2}\bar u_{\text{g}}^2}}{{{{\bar r}_i}}}, \hfill \\ \end{gathered} $

(22)

式中，u_g、c为螺旋气流平均速度和界面波波速，满足速度三角关系：

$ \begin{gathered} {{\bar u}_z} = \bar u\cos \theta ,{c_z} = c\cos \theta , \hfill \\ {{\bar u}_\theta } = \bar u\sin \theta ,{c_\theta } = c\sin \theta . \hfill \\ \end{gathered} $

(23)

1.2.2 液相场

螺旋环状流中，管壁液膜厚度相对于管径足够小，可以将液膜的流动简化为二维流动。实际流动过程中，周向分速度促使液膜产生远离旋转中心的离心运动，离心力作为附加正应力作用于相界面影响其稳定性。在分析液膜运动特性时，首先将此离心力作为源项引入动量方程。二维直角坐标系下，令y=R_o－r，液膜运动的控制方程^[13]可表示为：

$ \begin{gathered} \frac{{\partial {u_y}}}{{\partial y}} + \frac{{\partial {u_s}}}{{\partial s}} = 0, \hfill \\ {u_y}\frac{{\partial {u_y}}}{{\partial y}} + {u_z}\frac{{\partial {u_y}}}{{\partial z}} + \frac{{u_\theta ^2}}{{{{\bar r}_i}}} = - \frac{1}{{{\rho _1}}}\frac{{\partial p}}{{\partial y}}, \hfill \\ {u_y}\frac{{\partial {u_z}}}{{\partial y}} + {u_z}\frac{{\partial {u_z}}}{{\partial z}} = - \frac{1}{{{\rho _l}}}\frac{{\partial p}}{{\partial z}}. \hfill \\ \end{gathered} $

(24)

其中，周向速度u_θ=u_zsinθ。

与气相场类似的分析方法，得到液膜作用于相界面y=δ的正应力扰动量$ {{\hat N}_{il}} $

$ {{\hat N}_{i{\text{l}}}} = \frac{{{\rho _1}{k^2}\hat \delta \bar \delta {{\left( {{{\bar u}_1} - c} \right)}^2}}}{2} - \frac{{{\rho _1}\hat \delta {{\left( {\sin \theta } \right)}^2}\bar u_1^2}}{{{{\bar r}_i}}}. $

(25)

因此，螺旋环状流中气液两相作用于相界面的正应力可分别表示为：

$ {N_{ig}} = {{\bar N}_{ig}} + \left[ { - {\rho _{\text{g}}}k\hat \delta {{\left( {{{\bar u}_g} - c} \right)}^2} - \frac{{{\rho _g}\hat \delta {{\left( {\sin \theta } \right)}^2}\bar u_g^2}}{{{{\bar r}_i}}}} \right]{{\text{e}}^{{\text{i}}kz}}, $

(26)

$ {N_{i{\text{l}}}} = {{\bar N}_{i{\text{l}}}} + \left[ {\frac{{{\rho _1}{k^2}\hat \delta \bar \delta {{\left( {{{\bar u}_1} - c} \right)}^2}}}{2} - \frac{{{\rho _1}\hat \delta {{\left( {\sin \theta } \right)}^2}\bar u_1^2}}{{{{\bar r}_i}}}} \right]{{\text{e}}^{{\text{i}}kz}}. $

(27)

其中，N_ig、N_il分别为平均气相正应力和平均液相正应力。

1.3 界面稳定性条件

根据界面波波峰处两相正应力与表面张力平衡条件 (图 2)，进行界面稳定性分析。

$ {N_{i{\text{l}}}} - {N_{ig}} = \sigma \chi , $

(28)

其中，σ为表面张力系数。

$ \chi = {k^2}\hat m{{\text{e}}^{{\text{i}}kz}}. $

(29)

将式 (26)、(27) 及 (29) 代入方程 (28)，得到界面稳定性控制方程

$ \begin{array}{*{20}{c}} {{\rho _1}{{\left( {{{\bar u}_1} - c} \right)}^2}\frac{1}{2}k\bar \delta + {\rho _{\text{g}}}{{\left( {{{\bar u}_g} - c} \right)}^2} = k\sigma + } \\ {\frac{{{{\left( {\sin \theta } \right)}^2}\left( {{\rho _1}\bar u_1^2 - {\rho _{\text{g}}}\bar u_{\text{g}}^2} \right)}}{{{{\bar r}_i}k}}.} \end{array} $

(30)

求解上述方程，得到界面波波速的复数解

$ {c_{\text{R}}} = \frac{{\frac{1}{2}k\bar \delta {\rho _1}{{\bar u}_1} + {\rho _{\text{g}}}{{\bar u}_{\text{g}}}}}{{\frac{1}{2}k\bar \delta {\rho _1} + {\rho _{\text{g}}}}}, $

(31)

$ \begin{array}{*{20}{c}} {{c_1} = \frac{1}{{\frac{1}{2}k\bar \delta {\rho _1} + {\rho _{\text{g}}}}}\left\{ {\frac{1}{2}{\rho _1}{\rho _{\text{g}}}k\bar \delta {{\left( {{{\bar u}_g} - {{\bar u}_1}} \right)}^2} - } \right.} \\ {{{\left. {\left[ {k\sigma + \frac{{{{\left( {\sin \theta } \right)}^2}\left( {{\rho _1}\bar u_1^2 - {\rho _{\text{g}}}\bar u_{\text{g}}^2} \right)}}{{{{\bar r}_i}k}}} \right]\left( {\frac{1}{2}{\rho _1}k\bar \delta + {\rho _{\text{g}}}} \right)} \right\}}^{\frac{1}{2}}}} \end{array} $

(32)

由中性稳定条件β_I=kc_I=0，得到稳定性判断准则

$ k\sigma + \frac{{{{\left( {\sin \theta } \right)}^2}\left( {{\rho _1}\bar u_1^2 - {\rho _{\text{g}}}\bar u_{\text{g}}^2} \right)}}{{{{\bar r}_i}k}} > \frac{{\frac{1}{2}{\rho _1}{\rho _{\text{g}}}k\bar \delta {{\left( {{{\bar u}_g} - {{\bar u}_1}} \right)}^2}}}{{\frac{1}{2}{\rho _1}k\bar \delta + {\rho _{\text{g}}}}}. $

(33)

准则式 (33) 表明，界面的扰动及波的成长决定于3个力的相互作用：气液相对运动产生的气动力，促使扰动增大，是不稳定因素；表面张力抑制界面的变形，起稳定作用；离心力对界面的作用取决于气液各相动压 ($ {\rho _{\rm{g}}}\bar u_{\rm{g}}^2 $、$ {\rho _{\rm{1}}}\bar u_{\rm{1}}^2 $) 的相对大小及旋流强度 (sinθ)。一定液膜流动条件下，存在临界气流速度$ {{\bar u}_{gc}} = \sqrt {{\rho _1}/{\rho _g}} {{\bar u}_l} $：当u_g>u_gc时，离心力为不稳定作用力；当u_g < u_gc时，离心力为稳定作用力；当u_g=u_gc时，离心力对界面波的稳定性不产生影响。这与Matas等^[14]，Jeon等^[15]及Im等^[16]的实验研究定性规律是一致的。

当旋流强度θ=0时，准则式同Hewitt和Hall-Taylor^[11]给出的传统环状流中液膜流动稳定性准则相同。当式 (33) 中离心力项$ {\left( {sin\theta } \right)^2}({\rho _{\rm{l}}}{{\bar u}^2}_{\rm{l}}-{\rho _{\rm{g}}}{{\bar u}^2}_{\rm{g}})/{{\bar r}_i} $由重力项 (ρ_l-ρ_g)g替换后，准则式同Barnea和Taitel^[17]以及Ishii和Hibiki等^[18]给出的水平管内气液分层流稳定性准则一致。此外，当气液轴向速度为0，且只存在周向类似刚体的圆周运动时，上述准则式转变为${(k{{\bar r}_i})^2} + \frac{{({\rho _{\rm{l}}}{{\bar u}^2}_{{\rm{l}}\theta }-{\rho _{\rm{g}}}{{\bar u}^2}_{{\rm{g}}\theta }){{\bar r}_i}}}{\sigma } > 0$，这与Rosenthal^[19]得到的旋转圆筒内分层流体界面稳定性准则一致。同时，当分层两流体的密度相当或内层流体密度可以忽略时，等价于单相流体的情况，如旋转液柱/液环自由表面的稳定性问题，此时，准则式$ {(k{{\bar r}_i})^2} + \frac{{({\rho _{\rm{l}}}{{\bar u}^2}_{{\rm{l}}\theta }-{\rho _{\rm{g}}}{{\bar u}^2}_{{\rm{g}}\theta }){{\bar r}_i}}}{\sigma } > 0 $转变为$ {(k{{\bar r}_i})^2} + \frac{{{\rho _{\rm{l}}}{{\bar u}^2}_{{\rm{l}}\theta }{{\bar r}_i}}}{\sigma } $(液柱) 及$ \frac{{{\rho _{\rm{l}}}{{\bar u}^2}_{{\rm{l}}\theta }{{\bar r}_i}}}{\sigma } > {(k{{\bar r}_i})^2} $(圆管内壁液膜)，分别与Hocking^[20]及Pedley^[21]得到的稳定性准则一致。因此，本文推导的理论判断准则具有通用性。

2 结果分析 2.1 扰动增长特性曲线

为深入分析螺旋环状流中界面波的动力学特性，计算结果给出工质为空气-水的流动稳定性特征曲线，包括扰动增长率特性曲线、中性稳定性曲线和最快速波特性曲线，并系统分析气速、旋流强度及管径对界面波稳定性的影响规律。

图 3给出一定液膜流速u_l=1.72 m/s和波长λ=10 mm，不同旋流强度θ和管径R_o条件下，扰动增长率β_I随气速u_g的变化曲线。由图可知，存在临界气速u_gc=49.5 m/s将液膜的流动分为2个特征区域：当u_g < u_gc时，离心力对液膜流动为稳定因素，这时离心力越大，即旋流强度θ越大、管径R_o越小，扰动增长率β_I越小，液膜流动稳定性增强；相反，当u_g>u_gc时，离心力转变为不稳定作用力，不稳定离心力与气液相对运动的气动力共同作用加剧了液膜流动的不稳定性。此外，由图可知，当气速较小时，θ越大、R_o越小，对应起稳定作用的离心力越大，此时，离心力与表面张力的稳定作用足以克服不稳定气动力，β_I小于0，界面扰动衰减，液膜流动趋于稳定。

2.2 中性稳定性曲线

当扰动增长率β_I=0时，对应的波长称为临界波长λ_c。而λ_c－u_g曲线称为中性稳定曲线。在中性稳定曲线上，扰动稳定不变，液膜流动处于临界稳定状态；一旦有扰动触发，流动状态随时可能改变，进入稳定区域或不稳定区域。中性稳定曲线下方，界面波波长小于临界值，扰动增长率β_I小于0，扰动衰减，为稳定流动区；在中性稳定曲线上方，β_I始终大于0，扰动增大，为不稳定流动区。图 4给出不同旋流强度θ和管径R_o条件下的中性稳定曲线。由图可知，一定液速下，λ_c随着u_g的增大而急剧减小。当气速较小时，起稳定作用的离心力对中性稳定波有重要影响，θ越大、R_o越小，波长临界值λ_c越大，中性稳定曲线上移，稳定区域变大，液膜流动稳定性增强；随着气速的增大，离心力对界面波稳定作用逐渐减弱直至消失并转变为不稳定影响，此时，界面波主要受不稳定气动力控制，因此，旋流强度θ和管径R_o对中性稳定波的影响可忽略。

2.3 最快速波特性曲线

当扰动增长率达到最大值 (β_I)_max时，界面波处于最不稳定状态，气液相界面极易失稳破碎。此时，界面波称为最快速波或最危险波。图 5给出不同旋流强度θ和管径R_o条件下，最快速波波长λ_max的特性曲线。与中性稳定曲线相同 (图 5)，λ_max随气速的增大而急剧减小。然而，当气速较小时，旋流强度θ和管径R_o对最不稳定状态的界面波波长没有影响，即离心力不改变界面波失稳破裂时对应的波长大小，气液相对运动的气动力是控制界面波失稳的主导作用力。

3 结论

螺旋环状流中，两相螺旋涡流通过不同旋流强度下离心力的作用重新分配相界面处力平衡关系，对液膜流动的水动力特性及其稳定性产生重要影响。本文利用Kelvin-Helmholtz不稳定性理论及双流体模型，考虑旋流的影响，通过分析气液两相作用于相界面的力平衡条件，建立螺旋涡流作用下界面波的动力学模型，获得界面失稳的临界条件和稳定性判断准则，并与现有的理论模型进行对比验证。基于本文提出的准则条件，系统分析气速、旋流强度及管径的影响规律，得到螺旋涡流对界面波稳定性的影响取决于气液两相动压相对大小这一重要认识。主要结论如下：

1) 对一定的液膜流速，当气速小于临界值时，离心力为稳定作用力，旋流强度越大、管径越小，界面波越稳定；当气速大于临界值时，离心力为不稳定作用力；旋流强度越大、管径越小，界面波越不稳定；当气速等于临界值时，离心力对界面波的稳定性不产生影响。

2) 临界波长随着气速的增大而急剧减小，当气速较小时，旋流强度越大、管径越小，波长临界值越大，中性稳定曲线上移，稳定区域变大，液膜流动稳定性增强；随着气速的持续增大，旋流强度和管径对中性稳定波的影响逐渐减弱至可忽略。

3) 最快速波波长随气速的增大而急剧减小，在不同气速条件下，旋流强度和管径对最不稳定状态的界面波波长不产生影响。