2. 北京石油化工学院机械工程学院, 北京 102617
2. School of Mechanical Engineering, Beijing Institute of Petrochemical Technology, Beijing 102617, China
气-固两相湍流广泛存在于各种工业过程中,特别是在能源动力工业,化学工程和环保领域中,如电厂中煤粉的干燥、输运和燃烧,石化工业中的流态化反应床和各种类型的除尘设备,均涉及气-固两相流动[1-3]。因此深入研究气-固两相湍流的流动特征和相间作用机理,对于提高相应工业过程的效率和保护环境具有重要意义。在关于气-固两相湍流的众多研究中,基于点源模型 (particle-source-in-cell, PSIC) 的欧拉-拉格朗日直接数值模拟 (DNS) 是研究稀疏气-固两相湍流的湍流特征和相间作用的有力工具。在该方法中,气相湍流场通过直接求解纳维-斯托克斯方程获得,同时在拉格朗日坐标下追踪每一个颗粒的运动,并利用PSIC模型和硬球模型分别考虑相间作用和颗粒间碰撞。
显然,利用基于点源模型的欧拉-拉格朗日直接数值模拟研究稀疏气-固两相湍流时,准确描述颗粒受力是很重要的。许多模拟中的颗粒运动都是基于Maxey和Riley[4]的公式并进行相应简化来计算的,然而关于各相间作用力的取舍依然众说纷纭。例如Pan和Banerjee[5]考虑拖曳力、压力梯度力和重力;Dorgan和Loth[6]考虑颗粒所受的拖曳力和重力;Vance等[7]仅考虑拖曳力;Wang等[8]考虑拖曳力和升力;在Chen等[9]的直接数值模拟中,考虑颗粒所受的拖曳力、升力、布朗力和重力;Li等[10]考虑拖曳力、升力和重力;Yamamoto等[11]考虑颗粒所受的拖曳力、升力和重力;Nasr等[12]考虑颗粒所受的拖曳力和升力;Lain[13]考虑颗粒的拖曳力、重力、剪切升力和旋转升力。总体而言,大部分的研究者都会考虑拖曳力和重力,相当一部分研究者考虑颗粒所受的升力作用,而压力梯度力、Basset力和虚拟质量力通常被忽略。然而Elghobashi和Truesdell[14]指出Basset力是非重力方向上的重要作用力。
综上所述,在进行载有颗粒的两相流的直接数值模拟时,不同的研究者考虑不同的颗粒受力。因此有必要对槽道内颗粒的受力做一个综合的深入分析。本文通过理论分析和数值模拟相结合的方法研究颗粒在壁面约束湍流场中所受的各种相间力的相对大小,为后续气-固两相流模拟时颗粒受力的取舍提供依据。
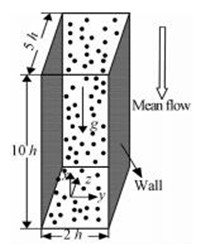
1 数值方法 1.1 连续相方程连续相流动区域如图 1所示,其中x,y,z分别表示流向、法向和展向,重力方向与流动方向一致,坐标系原点处于槽道底部的中心位置。流动区域在x,y,z这3个方向上的尺度分别为10h,2h,5h (等于1 500×300×750个νg/uτ,即壁面单元尺度,其中νg是气体的运动黏性系数,uτ为摩擦速度),其中h是槽道半宽。连续相流场通过对室温下不可压缩流体的纳维-斯托克斯方程进行直接数值求解得到,颗粒对流体的反作用通过PSIC模型来考虑,并以单位质量力的形式作用在连续相中。对流动的长度、速度和时间相关的量分别用h、uτ和h/uτ进行无量纲化后,连续相的无量纲控制方程可表述如下:
|
Download:
|
|
图 1 流动区域图示 Fig. 1 Schematic of the channel flow |
|
| $ \frac{{\partial u_{{{\text{g}}_i}}^ + }}{{\partial x_i^ * }} = 0, $ | (1) |
| $ \begin{gathered} \frac{{\partial u_{{{\rm{g}}_i}}^ + }}{{\partial {t^ * }}} + u_{{{\rm{g}}_i}}^ + \frac{{\partial u_{{{\rm{g}}_i}}^ + }}{{\partial t_j^ * }} = - \frac{{\partial {p^ + }}}{{\partial x_i^ * }} + {\delta _{1i}} + \hfill \\ \frac{1}{{\mathit{R}{\mathit{e}_\tau }}}{\nabla ^2}u_{{{\rm{g}}_i}}^ + - S_{{\rm{up}}i}^ + , \hfill \\ \end{gathered} $ | (2) |
式中:ugi+和p+分别表示气相的速度和脉动压力;δ1i是克罗内克符号;Reτ是摩擦雷诺数,其定义式为Reτ=huτ/νg,本文所研究的初始流动Reτ的值为150;Supi+为当地颗粒对流体的无量纲反作用力,通过对流体单位质量所受的作用力采用ρguτ2/h进行无量纲化而得到,其中ρg为气相密度。
在模拟中,以达到稳定状态的壁面湍流作为初始条件。x,z方向的流入流出界面设置为周期性边界条件,而在y方向的壁面设为无滑移壁面边界条件。采用有限差分法对流体相的控制方程进行离散求解,其中在x和z方向用均匀网格,在y方向为非均匀网格,整个网格系统为128×128×12。采用二阶中心差分格式进行空间离散,显式的Adams-Bashforth时间分裂格式被用来推进求解速度,但是压力项通过隐式表达式计算,并且通过求解压力泊松方程进行压力速度耦合。采用交错网格系统以防止棋盘型的压力场的出现。
1.2 颗粒运动方程颗粒相是在连续相达到统计稳态之后加入的,其初始分布是均匀的。颗粒相的参数根据Kulick等[15]和Yamamoto等[11]按照基于壁面时间单元尺度的斯托克斯数St相等的原则进行设置,颗粒参数的具体设置如表 1所示。
|
|
表 1 颗粒相的计算参数 Table 1 Properties of particles |
表中:ρp和dp为固体颗粒的密度和直径;α0、St、Np和ml分别表示颗粒平均体积分数、颗粒斯托克斯数、颗粒总数目和气-固两相湍流的质量载率。
颗粒相在湍流场中的运动用牛顿运动定律描述,颗粒受力包括BBO方程中的所有力,此外颗粒所受的剪切升力和旋转升力也一并考虑。颗粒的无量纲运动方程如下:
| $ \begin{gathered} \left( {\frac{{{\rho _{\rm{p}}}}}{{{\rho _{\rm{g}}}}}} \right)\frac{{{\rm{d}}\mathit{\boldsymbol{u}}_{\rm{p}}^ + }}{{{\rm{d}}{t^ * }}} = \frac{3}{4}{C_{\rm{D}}}{C_{\rm{W}}}\frac{1}{{d_{\rm{p}}^ * }}\left| {\mathit{\boldsymbol{u}}_{\rm{g}}^ + - \mathit{\boldsymbol{u}}_{\rm{p}}^ + } \right|\left( {\mathit{\boldsymbol{u}}_{\rm{g}}^ + - \mathit{\boldsymbol{u}}_{\rm{p}}^ + } \right) + \hfill \\ \frac{9}{{\sqrt {\rm{ \mathsf{ π} }} }}\frac{1}{{d_{\rm{p}}^ * }}\frac{1}{{\sqrt {\mathit{R}{\mathit{e}_\tau }} }}\int_{t_{{{\rm{p}}_0}}^ * }^{t_{\rm{p}}^ * } {\frac{{{\rm{d}}\left( {\mathit{\boldsymbol{u}}_{\rm{g}}^ + - \mathit{\boldsymbol{u}}_{\rm{p}}^ + } \right)}}{{{\rm{d}}{\tau ^ * }}}} \frac{1}{{\sqrt {t_{\rm{p}}^ * - {\tau ^ * }} }}{\rm{d}}{\tau ^ * } + \hfill \\ \frac{{{C_{{\rm{LS}}}}}}{{\sqrt {\mathit{R}{\mathit{e}_\tau }} }}\frac{1}{{d_{\rm{p}}^ * }}\left( {\mathit{u}_{{\rm{g}}x}^ + - \mathit{u}_{{\rm{p}}x}^ + } \right){\left| {\frac{{{\rm{d}}\mathit{u}_{{\rm{g}}x}^ + }}{{{\rm{d}}y}}} \right|^{1/2}}{\rm{Sign}}\left( {\frac{{{\rm{d}}\mathit{u}_{{\rm{g}}x}^ + }}{{{\rm{d}}y}}} \right) + \hfill \\ \frac{3}{4}{C_{{\rm{LR}}}}\frac{1}{{d_{\rm{p}}^ * }}\left| {\mathit{\boldsymbol{u}}_{\rm{g}}^ + - \mathit{\boldsymbol{u}}_{\rm{p}}^ + } \right|\left( {\mathit{\boldsymbol{u}}_{\rm{g}}^ + - \mathit{\boldsymbol{u}}_{\rm{p}}^ + } \right) \times \frac{{\left( {\mathit{\boldsymbol{\omega }}_{\rm{g}}^ + - \mathit{\boldsymbol{\omega }}_{\rm{p}}^ + } \right)}}{{\left| {\mathit{\boldsymbol{\omega }}_{\rm{g}}^ + - \mathit{\boldsymbol{\omega }}_{\rm{p}}^ + } \right|}} + \hfill \\ {C_{\rm{V}}}\left( {\frac{{D\mathit{\boldsymbol{u}}_{\rm{g}}^ + }}{{D{t^ * }}} - \frac{{{\rm{d}}\mathit{\boldsymbol{u}}_{\rm{p}}^ + }}{{{\rm{d}}{t^ * }}}} \right) + \frac{{D\mathit{\boldsymbol{u}}_{\rm{g}}^ + }}{{D{t^ * }}} + {\delta _{1i}}\left( {\frac{{{\rho _{\rm{p}}}}}{{{\rho _{\rm{g}}}}} - 1} \right)\frac{1}{{F{r^2}}}. \hfill \\ \end{gathered} $ | (3) |
式中:up+是颗粒的无量纲速度,ug+表示颗粒位置处的气体速度;ωp+和ωg+分别表示颗粒旋转角速度以及颗粒位置处流体的旋转角速度;CV和CD分别表示虚拟质量力系数和拽力系数,对于球形颗粒CV的值为0.5,CD通过Pang等[16]给出的经验公式来计算,CW是对拖曳力的近壁面修正,其计算式见文献[5];CLS和CLR分别是剪切升力系数和旋转升力系数,CLS的计算方法与Li等[10]一致,旋转升力系数根据Yamamoto等[11]的表达式来计算;Fr是弗劳德数,定义式为
颗粒的旋转运动是引起颗粒旋转升力的原因,而且颗粒的旋转在颗粒二元碰撞时具有重要影响。因此在计算中也考虑颗粒的旋转运动,其计算公式如下
| $ \frac{{{\rho _{\rm{p}}}}}{{{\rho _{\rm{g}}}}}\frac{{{\rm{d}}\mathit{\boldsymbol{\omega }}_{\rm{p}}^ + }}{{{\rm{d}}{t^ * }}} = - {C_{\rm{T}}}\left| {\mathit{\boldsymbol{\omega }}_{\rm{p}}^ + - \mathit{\boldsymbol{\omega }}_{\rm{g}}^ + } \right|\left( {\mathit{\boldsymbol{\omega }}_{\rm{p}}^ + - \mathit{\boldsymbol{\omega }}_{\rm{g}}^ + } \right), $ | (4) |
其中CT是与颗粒旋转雷诺数相关的无量纲系数,其具体计算式参见文献[11]。
颗粒的初始位置为随机分布,颗粒的初始速度和旋转速度与颗粒位置处的流体速度和旋转速度一致。颗粒在流向和展向采用周期性边界条件,而在法向上颗粒与壁面发生碰撞。采用二阶的Crank-Nicholson方法进行颗粒速度、位移和旋转角速度的推进。
1.3 四向耦合在本研究中采用基于颗粒点源模型PSIC的力耦合模型考虑颗粒对连续相的反作用。颗粒对流体相的反作用力通过体积平均的方法加载到颗粒中心位置所在的网格单元上,其表达式如式 (5) 所示。因为网格系统是交错的,所以反作用力存储在网格单元中心点上,而速度存储在网格单元的界面上,故需要对颗粒反作用力进行插值以获得修正的速度值。
| $ S_{{\rm{up}}}^ + = - \frac{{{\rho _{\rm{p}}}{V_{\rm{p}}}}}{{{\rho _{\rm{g}}}\Delta x\Delta y\Delta z}}\sum\limits_{j = 1}^M {\left( {\mathit{\boldsymbol{a}}_j^ * - {g^ * }\left( {1 - \frac{{{\rho _{\rm{g}}}}}{{{\rho _{\rm{p}}}}}} \right)} \right)} , $ | (5) |
式中:VP是颗粒体积;M为 (i, j, k) 网格单元内包含的颗粒数目;Δx、Δy、Δz分别为该网格单元在3个坐标轴方向上的网格间距。颗粒相的时间步长为气相时间步长的1/10,两相的计算时间进行等值匹配,也就是说每进行一次气相的流动状态更新,颗粒相沿时间推进10步,因此相间作用力需要通过对颗粒在整个气相时间步长的反作用力进行平均而得到。
在以往的研究中发现,即使是在稀疏的气-固两相流中,颗粒间的碰撞对颗粒速度和分布也具有显著影响,而且颗粒间碰撞对Basset力会产生较大影响。因此在模拟中也应考虑颗粒间碰撞,这就是通常意义上的两相流模拟中的四向耦合方法。颗粒间碰撞采用硬球模型,并且采用分块搜索方法来确定碰撞对 (Npi,Npj)。由于在本文的模拟中,颗粒的数密度不高,因此颗粒间主要发生二元碰撞。当考虑颗粒与壁面之间的碰撞时,将壁面看作是无限大的静止颗粒。
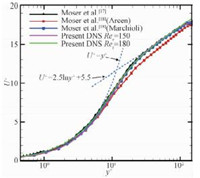
1.4 数值方法验证本文所采用的湍流直接数值模拟方法可以通过比较流向平均速度分布曲线的分布进行验证。图 2给出不同研究中的流向平均速度分布。其中Moser等[17]的研究中摩擦雷诺数为180,而在Marchioli等[18]开展的国际联合测试中其值为150。从图中可以看出,本文采用的直接数值模拟方法所得的平均速度分布曲线与经典的对数律吻合很好。此外,在2种摩擦雷诺数下,本文方法所得结果与前人的直接数值模拟结果均吻合较好。因此可以认为本文采用的湍流直接数值模拟方法是可靠的。
|
Download:
|
|
图 2 流向平均速度分布曲线的比较 Fig. 2 Comparison of the mean streamwise velocity profile |
|
颗粒所受作用力的相对大小可以采用理论分析的方法来估算。由于气-固两相流中的颗粒流体密度比普遍较大,因此颗粒所受的重力非常重要,其相对大小不需要估算,剩下需要估算相对大小的均是两相间作用力。在颗粒所受的各种相间作用力中,颗粒所受的拖曳力是最重要的,因此可以将拖曳力作为标准估算其他相间作用力的相对大小。而且为便于分析,拖曳力的大小采用未修正Stokes拖曳力公式来描述,其余的相间力也采用未修正的计算公式。
根据各个相间力的物理意义,可以将它们分为两组:1) Basset力和虚拟质量力,其产生机理在于颗粒相对于流体做非恒定运动;2) 剪切升力、旋转升力和流体加速力, 其产生机理在于颗粒在非均匀的流场中运动。第1组相间力的本质在于两相流动状态在时间上不均匀产生,因此可以采用频率分析的方法考察其大小。第2组相间力的本质在于两相流动状态在空间上是不均匀的,从而可以采用流体量级估算法考察其大小。
首先采用频率分析法估算Basset力和虚拟质量力相对于拖曳力的大小。根据Pan和Banerjee[5], 不同尺度的连续相均会对小颗粒运动产生影响,因此在湍流场中,两相间的相对速度ur(t) 可以表示为如下形式:
| $ {\mathit{\boldsymbol{u}}_{\rm{r}}}\left( t \right) = {\mathit{\boldsymbol{u}}_{\rm{g}}} - {\mathit{\boldsymbol{u}}_{\rm{p}}} = \sum\limits_\mathit{\boldsymbol{\omega }} {{{\hat u}_{\rm{r}}}\left( \mathit{\boldsymbol{\omega }} \right){{\rm{e}}^{i\omega t}}} , $ | (6) |
式中ω是频率,而
| $ \hat F_{\rm{D}}^ + = 3{\rm{ \mathsf{ π} }}d_{\rm{p}}^ + \hat u_{\rm{r}}^ + \left( {{\mathit{\boldsymbol{\omega }}^ + }} \right), $ | (7) |
| $ \hat F_{\text{B}}^ + = {\lambda ^ + }\hat F_{\text{D}}^ + /2, $ | (8) |
| $ \hat F_{{\text{AM}}}^ + = {\lambda ^{ + 2}}\hat F_{\text{D}}^ + /36. $ | (9) |
其中
第2组的相间力相对于拖曳力的大小可以用量级分析法来估算。因为这些力都是由流场的不均匀性直接或间接产生的,故可以采用流体相的特征速度 uτ, 特征长度 h, 特征时间 h/uτ 对受力公式的相应项进行比拟。因此剪切升力、旋转升力和压力梯度力与拖曳力的比值可以做如下简化:
| $ \begin{array}{*{20}{c}} {\frac{{{\mathit{\boldsymbol{F}}_{{\rm{LS}}}}}}{{{\mathit{\boldsymbol{F}}_{\rm{D}}}}} = \frac{{1.62d_{\rm{p}}^2{\rho _{\rm{g}}}{{\left( {{\mathit{\boldsymbol{v}}_{\rm{g}}}\left| {\frac{{{\rm{d}}{\mathit{u}_{{\rm{g}}x}}}}{{{\rm{d}}y}}} \right|} \right)}^{1/2}}\left( {{\mathit{u}_{{\rm{g}}x}} - {\mathit{u}_{{\rm{p}}x}}} \right)}}{{3{\rm{ \mathsf{ π} }}{\mathit{\boldsymbol{v}}_{\rm{g}}}{\rho _{\rm{g}}}{d_{\rm{p}}}\left( {{\mathit{\boldsymbol{u}}_{\rm{g}}} - {\mathit{\boldsymbol{u}}_{\rm{p}}}} \right)}}} \\ { \sim \frac{{{d_{\rm{p}}}}}{h}\sqrt {\frac{{h{u_\tau }}}{{{\mathit{\boldsymbol{v}}_{\rm{g}}}}}} = \frac{{{d_{\rm{p}}}}}{h}\sqrt {\mathit{R}{\mathit{e}_\tau }} ,} \end{array} $ | (10) |
| $ \begin{array}{*{20}{c}} {\frac{{{\mathit{\boldsymbol{F}}_{{\rm{LR}}}}}}{{{\mathit{\boldsymbol{F}}_{\rm{D}}}}} = \frac{{\frac{{\rm{ \mathsf{ π} }}}{{32}}d_{\rm{p}}^3{\rho _{\rm{g}}}\left( {{\mathit{\boldsymbol{u}}_{\rm{g}}} - {\mathit{\boldsymbol{u}}_{\rm{p}}}} \right) \times \left( {{\mathit{\boldsymbol{\omega }}_{\rm{g}}} - {\mathit{\boldsymbol{\omega }}_{\rm{p}}}} \right)}}{{3{\rm{ \mathsf{ π} }}{\mathit{\boldsymbol{v}}_{\rm{g}}}{\rho _{\rm{g}}}{d_{\rm{p}}}\left( {{\mathit{\boldsymbol{u}}_{\rm{g}}} - {\mathit{\boldsymbol{u}}_{\rm{p}}}} \right)}}} \\ { \sim \frac{{d_{\rm{p}}^2}}{{{\mathit{\boldsymbol{v}}_{\rm{g}}}}}\frac{{{u_\tau }}}{h} = {{\left( {\frac{{{d_{\rm{p}}}}}{h}} \right)}^2}\mathit{R}{\mathit{e}_\tau },} \end{array} $ | (11) |
| $ \frac{{{\mathit{\boldsymbol{F}}_{\rm{P}}}}}{{{\mathit{\boldsymbol{F}}_{\rm{D}}}}} = \frac{{\frac{{\rm{ \mathsf{ π} }}}{6}d_{\rm{p}}^3{\rho _{\rm{g}}}\frac{{D{u_{\rm{g}}}}}{{Dt}}}}{{3{\rm{ \mathsf{ π} }}{\mathit{\boldsymbol{v}}_{\rm{g}}}{\rho _{\rm{g}}}{d_{\rm{p}}}\left( {{\mathit{\boldsymbol{u}}_{\rm{g}}} - {\mathit{\boldsymbol{u}}_{\rm{p}}}} \right)}} \sim \frac{{d_{\rm{p}}^2}}{{{\mathit{\boldsymbol{v}}_{\rm{g}}}}}\frac{{{u_\tau }}}{h} = {\left( {\frac{{{d_{\rm{p}}}}}{h}} \right)^2}\mathit{R}{\mathit{e}_\tau }. $ | (12) |
将本文研究的颗粒与连续相参数代入各模型力与拖曳力的相对大小比较公式中,可得各模型力的相对大小如表 2所示。从表中可以看出,Basset力和剪切升力相对于Stokes拖曳力来说具有相当的重要性,而虚拟质量力、旋转升力和压力梯度力相对于Stokes拖曳力来说是非常小的。
|
|
表 2 颗粒所受各作用力与Stokes拖曳力之比的理论估算值 Table 2 Ratios of interphase forces to Stokes drag evaluated by using theoretical method |
在气-固两相湍流的直接数值模拟中,随机选取某一个颗粒,输出该颗粒所受的各相间力产生的无量纲加速度随计算时间的变化。必须注意的是,在计算Basset力的时候,以颗粒的弛豫时间和湍流柯氏时间微尺度分别作为积分时间尺度和积分时间步长。为方便起见,这里仅给出铜颗粒所受各作用力。
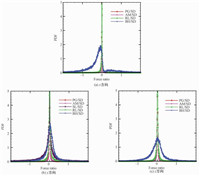
3个方向上各作用力与拖曳力比值的概率密度分布 (PDF) 如图 3所示,从图中可以看出在x和z方向上,Basset力相对于拖曳力来说具有相当的大小,而压力梯度力、虚拟质量力和旋转升力则可忽略。从y方向上各作用力与拖曳力比值的概率密度分布也可看出除Basset力之外,剪切升力相对于拖曳力也是不可忽视的。
|
Download:
|
|
图 3 各作用力与拖曳力比值的PDF Fig. 3 PDF of the ratios of forces in different directions to drag force |
|
石松粉颗粒和铜颗粒在整个运动历程中各相间力与拖曳力的平均比值如表 3所示。总体上看,理论分析值与模拟计算值吻合较好,但是量级分析对石松粉所受剪切升力的预测似乎不太合理,因此需要对量级分析做进一步地研究。同时还可以看出:在x方向上,各相间力相对于拖曳力来说都较小,只有Basset力的值相对较大;在y方向上,Basset力和剪切升力相对于拖曳力来说均有较大的值,其余的相间力较小;在z方向上,除Basset力外,其余相间力的值均较小。
|
|
表 3 颗粒所受各相间力与拖曳力之比的模拟平均值 Table 3 Time average values of the ratios of different forces to drag force |
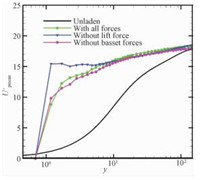
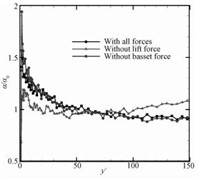
从单颗粒的受力中可以看出,颗粒受的剪切升力和Basset力比较重要,因此重点考察这两种相间力的影响。同样地,为方便起见,这里仅给出铜颗粒的结果。图 4给出不同工况下的颗粒平均速度分布曲线。从图中可以看到,剪切升力会使近壁面处的颗粒速度减小,而在不考虑Basset力时颗粒的流向速度也变得更小。这是因为剪切升力的存在会减弱颗粒的横向运动,而Basset力会在某种程度上促进颗粒的横向运动。这可以从不同工况下铜颗粒的局部体积分数分布图中得到佐证 (如图 5所示)。从理论上讲,颗粒的分布越均匀,那么颗粒的横向运动就越剧烈。显然,剪切升力会使颗粒更多地分布在壁面附近,而Basset力会减弱颗粒在壁面附近处的富集程度。因此从总体效果来看,剪切升力减弱颗粒的横向运动,而Basset力会促进颗粒的横向运动。
|
Download:
|
|
图 4 铜颗粒的平均速度分布曲线 Fig. 4 Mean streamwise velocity profiles |
|
|
Download:
|
|
图 5 铜颗粒的局部体积分数分布 Fig. 5 Profiles of volume fraction distribution |
|
本文从理论分析和数值计算两个方面对稀疏气-固两相湍流中颗粒所受的各相间力相对大小进行研究。结果表明,在相间力的计算公式适用范围内,通过频率分析和量级分析的方法确定各相间力相对于Stokes拖曳力的大小具有较高准确度。颗粒在重力方向主要受重力、拖曳力和Basset力的作用;在壁面法向,剪切升力、拖曳力和Basset力比较重要;而在展向方向上除拖曳力和Basset力之外的其他模型力均可忽略。值得一提的是,以往模拟中常被忽略的Basset力在气-固两相湍流中具有较大影响,不能轻易忽略。
| [1] | 周力行. 离散型湍流多相流动的研究进展和需求[J]. 力学进展, 2008, 38(5):610–622. |
| [2] | 李永明, 苏明旭, 袁安利, 等. 基于超声的管道内粉体体积分数的测量[J]. 中国科学院大学学报, 2016, 33(2):277–282. |
| [3] | 王帅, 刘国栋, 赵飞翔, 等. 循环流化床中颗粒聚团特性的模拟[J]. 化工学报, 2014, 65(6):2027–2033. |
| [4] | Maxey M R, Riley J J. Equation of motion for a small rigid sphere in a nonunifrom flow[J]. Physics of Fluids, 1983, 26(4):883–889. DOI:10.1063/1.864230 |
| [5] | Pan Y, Banerjee S. Numerical Simulation of particle interactions with wall turbulence[J]. Physics of Fluids, 1996, 8(10):2733–2755. DOI:10.1063/1.869059 |
| [6] | Dorgan A J, Loth E. Simulation of particles released near the wall in a turbulent boundary layer[J]. International Journal of Multiphase Flow, 2004, 30(6):649–673. DOI:10.1016/j.ijmultiphaseflow.2004.05.006 |
| [7] | Vance M W, Squires K D, Simonin O. Properties of the particle velocity field in gas-Solid turbulent channel flow[J]. Physics of Fluids, 2006, 18(6):2451–2466. |
| [8] | Wang Q, Squires K D, Chen M, et al. On the role of the lift force in turbulence simulations of particle deposition[J]. International Journal of Multiphase Flow, 1997, 23(4):749–763. DOI:10.1016/S0301-9322(97)00014-1 |
| [9] | Chen M, Kontomaris K, McLaughlin J B. Direct numerical simulation of droplet collisions in a turbulent channel flow. Part I:Collision algorithm[J]. International Journal of Multiphase Flow, 1998, 24(7):1079-1103. |
| [10] | Li Y M, McLaughlin J B, Kontomaris K, et al. Numerical simulation of particle-laden turbulent channel flow[J]. Physics of Fluids, 2001, 13(10):2957–2967. DOI:10.1063/1.1396846 |
| [11] | Yamamoto Y, Potthoff M, Tanaka T, Kajishima T, et al. Large-eddy simulation of turbulent gas-particle flow in a vertical channel:effect of considering inter-particle collisions[J]. Journal of Fluid Mechanics, 2001, 442(1):303–334. |
| [12] | Nasr H, Ahmadi G, McLaughlin J B. A DNS study of effects of particle-particle collisions and two-way coupling on particle deposition and phasic fluctuations[J]. Journal of Fluid Mechanics, 2009, 640(12):507–536. |
| [13] | Lain S. Study of turbulent two-phase gas-solid flow in horizontal channels[J]. Indian Journal of Chemical Technology, 2013, 20(2):128–136. |
| [14] | Elghobashi S, Truesdell G C. Direct simulation of particle dispersion in a decaying isotropic turbulence[J]. Journal of Fluid Mechanics, 1992, 242:655–700. DOI:10.1017/S0022112092002532 |
| [15] | Kulick J D, Fessler J R, Eaton J K. Particle response and turbulence modification in fully-developed channel flow[J]. Journal of Fluid Mechanics, 1994, 277:109–134. DOI:10.1017/S0022112094002703 |
| [16] | Pang M J, Wei J J, Yu B. Numerical investigation of phase distribution and liquid turbulence modulation in dilute particle-laden flow[J]. Particulate Science and Technology, 2011, 29(6):554–576. DOI:10.1080/02726351.2010.536304 |
| [17] | Moser R D, Kim J, Mansour N N. Direct numerical simulation of turbulent channel flow up to Reτ=590[J]. Physics of Fluids, 1999, 11(4):943–945. DOI:10.1063/1.869966 |
| [18] | Marchioli C, Soldati A, Kuerten J G M, et al. Statistics of particle dispersion in direct numerical simulations of wall-bounded turbulence:results of an international collaborative benchmark test[J]. International Journal of Multiphase Flow, 2008, 34(9):879–893. DOI:10.1016/j.ijmultiphaseflow.2008.01.009 |
 2017, Vol. 34
2017, Vol. 34