蒸汽在过冷水中射流凝结具有高效的传热传质能力,因而广泛应用于石油化工、航空航天、军工业和核工业等众多工业领域,如直接接触式换热器、水下推进系统,以及核反应堆的泄压系统等场合。
蒸汽在过冷水中射流凝结即蒸汽浸没射流凝结时,流场内会产生明显的压力振荡现象。压力振荡产生的冲击载荷对相关设备有重要影响,尤其振荡频率较低时甚至会发生共振,严重影响设备的安全运行和使用寿命。在核反应堆中,掺杂少量不凝结气体的高压高温蒸汽注射到换料水箱 (压水堆) 或者抑压池 (沸水堆) 过冷水的过程中,这些不凝结气体会影响汽水直接接触凝结换热及流动特性,进而影响射流凝结振荡频率及强度特性。研究不凝结气体对蒸汽浸没射流压力振荡特性的影响,对于改进相关工业设备的设计方法和运行技术具有十分重要的意义。
众多学者[1-3]对纯蒸汽喷射到过冷水中的直接接触换热现象进行了研究,但对含不凝结气体蒸汽浸没射流的研究仍然很缺乏。Song等[4-5]实验研究不凝结气体对蒸汽浸没射流压力振荡的影响,发现凝结振荡区的幅值随空气质量分数的增加先增大后逐渐减小。压力振荡峰值对应温度即阈值温度随空气质量分数的增加而逐渐降低,当空气质量分数由0%增加到5%时,凝结振荡区的阈值温度由70 ℃下降到40 ℃,而在稳定凝结区,其阈值温度由80 ℃下降到70 ℃,频率随空气质量分数的增加而减小。Kim等[6]也发现压力振荡频率随着空气质量分数的增加而减小,且在凝结振荡区,当空气质量分数为1%~2%时,幅值达到最大。
当蒸汽中含有少量不凝结性气体时,前人主要对凝结振荡区水箱壁面处的压力振荡进行了研究,而本文对含有不凝结性气体的蒸汽浸没射流流场内部的压力振荡进行实验研究,为存在此类现象的工业场合的设计与运行提供一定的参考。
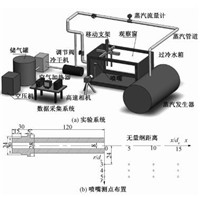
1 含不凝结性气体蒸汽浸没射流实验系统 1.1 实验系统含不凝结性气体蒸汽浸没射流的实验系统及压力测点布置如图 1所示,主要包括蒸汽系统、空气系统和测量系统等。
|
Download:
|
|
图 1 实验系统及测点布置示意图 Fig. 1 Schematic diagram of the system and the measuring point distribution |
|
蒸汽系统中采用全自动电热蒸汽锅炉,额定蒸发量为0.4 t·h-1,额定功率为330 kW。蒸汽质量流率通过涡街质量流量计测量,量程是27~469 kg/h,精度为1.0%FS。空气系统中螺杆式空气压缩机功率为55 kW,额定流量为7.5 m3·min-1,额定压力为1.3 MPa。空气加热器加热功率为6 kW,控温精度±1 ℃。空气质量流量计采用热式气体质量流量计,标况体积流量范围为0.16~16 m3/h,精度为0.5%FS,各项参数均可满足实验工况要求。
测量系统中T型热电偶的温度不确定度为±1 ℃。流场振荡压力的测量采用高频动态压力传感器,精度等级为0.2级。实验采用先进可靠的NI数据采集系统,采样频率为5 000 Hz,同时采用Labview作为仪器控制软件,为实验数据的采集和分析提供可靠的保证。
实验时,蒸汽和空气质量流量按一定的比例充分混合后,形成含不凝结性气体的饱和蒸汽,并通过喷嘴形成高速射流进入过冷水中。通过调节阀调节蒸汽和空气的质量流量,并用高频动态压力传感器测量不同工况时的压力振荡参数。
1.2 实验条件为了表明空气的含量对蒸汽浸没射流压力振荡的影响,空气含量采用空气质量流率与蒸汽质量流率的比值即空气质量分数来表示,空气质量分数A的表达式为
| $ A = \frac{{{G_{\text{a}}}}}{{{G_{\text{s}}}}} \times 100\% , $ | (1) |
Ga、Gs分别为空气和蒸汽质量流率,kg·m-2·s-1。
实验条件如表 1所示。
|
|
表 1 实验条件 Table 1 Experimental conditions |
为便于描述空间位置,定义两个参数,轴向、径向无量纲距离:
| $ X = \frac{x}{{{d_{\text{e}}}}}, $ | (2) |
| $ R = \frac{r}{{{d_{\text{e}}}}}, $ | (3) |
式中:x为实际轴向距离,mm;r为实际径向距离,mm;de为喷嘴出口直径,mm。
2 实验数据处理及实验结果的可靠性 2.1 实验数据处理通过压力振荡原始信号的均方根值来描述压力振荡整体趋势的变化,均方根值公式如下
| $ {p_{{\text{rms}}}} = {\left[ {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{p_i} - {p_{{\text{av}}}}} \right)}^2}} } \right]^{1/2}}, $ | (4) |
式中:pi为压力瞬时值,kPa;N为采点数量;pav为压力平均值,kPa,可通过下式计算获得
| $ {p_{{\text{av}}}} = \frac{1}{N}\sum\limits_{i = 1}^N {{p_i}} . $ | (5) |
实验中将压力振荡原始信号进行快速傅里叶变换,即由时域信号转化为频域信号,从频域信号中直接获取压力振荡频率特性。图 2所示为压力振荡原始信号的变化规律和时域信号经快速傅里叶变换后的频域信号,从图中可以看出压力振荡的强弱。

|
Download:
|
|
图 2 压力振荡原始信号和频谱分布 Fig. 2 Original signals of pressure oscillation and the frequency spectrum distribution |
|
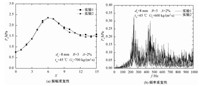
为验证实验结果的重现性,在相同工况下进行多次实验。对实验采集到的压力数据进行均方根处理和快速傅里叶变换,得到的振幅和频率的特性曲线如图 3所示。可以看出,实验的振幅曲线和频率曲线均几乎重合,从而表明,本文的实验结果具有良好的重现性。
|
Download:
|
|
图 3 压力振荡振幅和频率的重复性 Fig. 3 Repeatability of amplitude and frequency of pressure oscillation |
|
实验中存在不可避免的测量误差和系统误差,会影响实验结果准确性,所以需要对实验结果进行不确定度分析。本文使用Moffat[7]的方法对实验结果的不确定度进行分析。另外根据实验系统中测量仪器的精度,可以计算得出在本实验参数范围内蒸汽质量流率、空气质量流率、压力振荡的振荡强度和振荡主频的最大不确定度分别为1.0%、0.5%、16.2%和12.3%。
3 压力振荡实验结果与分析本文在不同的空气质量分数、蒸汽质量流率和过冷水温度下,利用高频动态压力传感器测量射流流场中的压力分布,从而找出汽水参数,尤其是不凝结性气体对射流压力振荡的影响规律,为分析蒸汽浸没射流的流动和凝结特性提出实验依据。
3.1 压力振荡强度不同空气质量分数下,压力振荡强度沿轴向无量纲距离的变化如图 4所示。压力振荡幅值随轴向距离的增加先增大后减小。当蒸汽中含不凝结性气体时,压力振荡幅值比纯蒸汽压力振荡幅值明显变小,且随着水温的升高,两振幅的相对差值逐渐减小。可以看出,不凝结气体对于蒸汽浸没射流的影响随着水温的升高而减小。

|
Download:
|
|
图 4 振荡幅值随轴向距离的变化 Fig. 4 Amplitude variation with axial distance |
|
压力振荡峰值随空气质量分数的增加,其位置沿轴向后移。这是由于空气质量分数增大总的质量流率增加,汽羽长度增大,随着空气质量分数增加,导致包裹在蒸汽泡外的不凝结气体层加厚,汽泡的体积越来越大,使得蒸汽在过冷水中凝结的过程中,热阻增加,凝结换热能力降低,从而减缓了蒸汽泡溃灭过程,凝结所需时间增长,峰值后移。
不同空气质量分数下,压力振荡强度随轴向无量纲距离的变化如图 5所示。实验结果表明,在一定蒸汽质量流率和过冷水温度下,压力振荡强度随不凝结性气体含量的增加整体呈下降趋势,且当空气质量分数小于2%时,振荡幅值减小较快,由此可见,在空气质量分数小于2%时,对压力振荡幅值的影响较大。

|
Download:
|
|
图 5 振荡幅值随过冷水温度的变化 Fig. 5 Amplitude variation with subcooled water temperature |
|
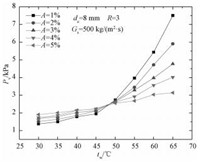
当空气质量分数一定时,压力振荡峰值随水温的升高而逐渐增大,且峰值位置沿轴向位置后移。这是由于随过冷水温的升高,其冷却能力逐渐下降,凝结周期增长,故振荡幅值越来越大。另外,蒸汽质量流率为500 kg·m-2·s-1时,不同空气质量分数下,压力振荡峰值随过冷水温的变化如图 6所示。分析可知:在水温低于45 ℃时,压力振荡峰值随空气质量分数的增加而逐渐增大;水温45~50 ℃之间时,峰值大小大致相同;水温高于50 ℃时,峰值随空气质量分数的增加而逐渐减小。
|
Download:
|
|
图 6 振荡峰值随过冷水温度的变化 Fig. 6 Variation in peak value with subcooled water temperature |
|
压力振荡是由于气液界面的波动而产生,此处可以通过不凝结性气体对气液相界面波动的影响来解释。当过冷水温度较低时,蒸汽被迅速凝结,汽羽长度相对较小。蒸汽中掺杂的少量空气将会阻碍气液界面传热,随着空气质量分数的增加,传热能力逐渐下降。汽羽形状膨胀,界面波动幅度增大。所以随着空气质量分数的增加,峰值逐渐增大。当过冷水温度较高时,过冷水冷凝能力下降,蒸汽不能够及时被冷凝,汽羽的长度增加,使得界面面积增加,流场中的影响范围增大,随着空气质量分数的增加,气液界面变得非常不稳定,波动愈加剧烈,汽羽边界形成不凝结性气体层,大量蒸汽被空气流携带向下游,所以随着空气质量分数的增加,峰值逐渐减小。
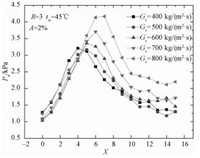
空气质量分数为2%时,不同蒸汽质量流率下,压力振荡强度随轴向无量纲距离的变化如图 7所示。由图中可以看出,压力振荡幅值随蒸汽质量流率的增加,峰值位置沿轴向后移。当空气质量分数一定时,压力振荡峰值随蒸汽质量流率的增加而逐渐增大。当蒸汽质量流率为400 kg·m-2·s-1时,凝结形态接近凝结振荡区,压力振荡峰值略高于500 kg·m-2·s-1时的压力振荡峰值。
|
Download:
|
|
图 7 振荡幅值随蒸汽质量流率的变化 Fig. 7 Amplitude variation with steam mass flux |
|
压力振荡第一主频随空气质量分数的变化如图 8所示。

|
Download:
|
|
图 8 第一主频随空气质量分数的变化 Fig. 8 Variation in the first frequency with air mass fraction |
|
实验结果表明,第一主频随空气质量分数的增大而减小,且空气质量分数较小时对蒸汽凝结压力振荡影响较为明显。由于不凝结性气体的存在,冷凝热阻变大,凝结时间增长,故使得振荡频率减小。当空气质量分数一定时,第一主频随过冷水温度的增加而逐渐减小,而且减小速度逐渐减缓。这是由于过冷水温度的升高导致其冷凝能力下降,使得凝结所需时间增加即凝结周期的增大,故第一主频逐渐减小。
当空气质量分数一定时,第一主频随蒸汽质量流率的增加而逐渐减小,且减小速度逐渐减慢。这是由于蒸汽质量流率的增加,汽羽的长度随之增加,相同时间内过冷水的冷凝能力下降即凝结所需时间增长,故压力振荡周期增加,第一主频逐渐减小。
同样,对压力振荡第二主频做统计分析,第二主频随空气质量分数的变化如图 9所示。结果表明,第二主频同样随着空气质量分数的增加而逐渐减小。当空气质量分数一定时,第二主频随过冷水温的增加而逐渐减小,随蒸汽质量流率的增加而逐渐减小,产生的原因与第一主频类似。

|
Download:
|
|
图 9 第二主频随空气质量分数的变化 Fig. 9 Variation in the second frequency with air mass fraction |
|
通过对含有不凝结性气体的蒸汽浸没射流进行实验,研究不凝结性气体对蒸汽浸没射流压力振荡特性的影响,得到以下主要结论:
1) 当蒸汽中含不凝结性气体时,压力振荡强度明显比纯蒸汽时小,且随着水温的升高,两振幅的差值相对逐渐减小。压力振荡峰值随空气质量分数的增加,其位置沿轴向后移。
2) 水温低于45 ℃时,峰值随空气质量分数的增加而逐渐增大;高于50 ℃时,随空气质量分数的增加而逐渐减小;水温在45~50 ℃之间时,峰值大致相同。当空气质量分数一定时,峰值随水温和蒸汽质量流率的增加而逐渐增大,且其位置沿轴向后移。
3) 压力振荡第一主频和第二主频均随着空气质量分数的增加而逐渐减小。当空气质量分数一定时,主频均随过冷水温度和蒸汽质量流率的增加而逐渐减小,而且减小速度逐渐减缓。
| [1] | Cho S, Song C H, Park C K, et al. Experimental study on dynamic pressure pulse in direct contact condensation of steam jets discharging into subcooled water[C]//1st Korea-Japan Symposium on Nuclear Thermal Hydraulics and Safety. Pusan, Korea, 1998:291-298. |
| [2] | Qiu B B, Tang S, Yan J J, et al. Experimental investigation on pressure oscillations caused by direct contact condensation of sonic steam jet[J]. Experimental Thermal and Fluid Science, 2014, 52:270–277. DOI:10.1016/j.expthermflusci.2013.09.020 |
| [3] | Qiu B B, Yan J J, Liu J P, et al. Experimental investigation on pressure oscillation frequency for submerged sonic/supersonic steam jet[J]. Annals of Nuclear Energy, 2015, 75:388–394. DOI:10.1016/j.anucene.2014.08.055 |
| [4] | Song C H, Cho S, Kwon T S. The effect of non-condensable gas on dynamic pressure induced by steam-water direct contact condensation[R]//Proc 5th Int Symp Heat Transfer Int. Beijing, China, 2000. |
| [5] | Song C H, Cho S, Kwon T S, et al. The effect of non-condensable gas on dynamic pressure induced by steam-water direct contact condensation[J]. Asme-Publications-Pvp, 2001, 421:193–200. |
| [6] | Kim K Y, Jeo S, Song C H, et al. The effect of the un-condensable gas on direct contact condensation in a pool[R]//Proceedings of the KNS spring meeting. 2000. |
| [7] | Moffat R J. Describing the uncertainties in experimental results[J]. Experimental Thermal and Fluid Science, 1988, 1(1):3–17. DOI:10.1016/0894-1777(88)90043-X |
 2017, Vol. 34
2017, Vol. 34 


