近期,政府各部门相继出台了一系列文件,鼓励和支持“互联网+”移动精准医疗健康发展。通过互联网与智能手机,将病人、医生和分级医疗资源相结合,提升现有医疗资源的使用效率,缓解“看病难”和“看病贵”的难题。移动精准医疗应用概括为疾病康复、远程医疗咨询、远程医疗监控和可穿戴设备检查等,核心是用户信息推荐和精准医疗服务,为用户提供精准信息服务,并研究面向移动精准医疗系统多层二分网络推荐算法。推荐算法是一种精准服务和信息过滤技术,帮助用户发现对自己有用的服务信息,给用户提供精准的信息服务。除协同过滤[1-2]和基于内容[3-4]等传统的推荐方法外,目前学术上提出了很多适用的推荐算法,如基于网格方法[5-9]、基于社交方法[10]、矩阵分解[11-12]和基于二分网络的推荐算法(bipartite network projection,BNP)[5-7]等等。
基于二分网络的推荐算法将用户和信息以节点表示,建立二分网络并存储相应关系,利用置信度传播的方式对用户进行推荐,如热传导传播[8]和随机游走推荐算法[9]等。然而,置信度在传统二分网络中不能得到充分传播,严重影响了推荐算法的准确性。此外,传统二分网络不能解决冷启动问题[13],即当新增加用户时,二分网络中该用户和其他信息节点无对应关系,则不能给该用户进行推荐。
为了能够更精确、更有效地推荐健康信息,本文提出一种面向移动健康医疗系统的多层二分网络推荐算法,并成功应用于移动健康医疗系统。
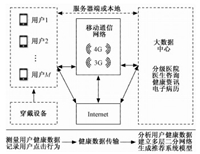
1 移动健康医疗推荐系统在移动健康医疗系统中,用户利用健康穿戴设备获得健康数据,通过移动网络和因特网将健康数据传送至服务器的移动健康医疗大数据中心。大数据中心对用户健康数据保存并分析,用户可随时根据服务器端或者本地存储的数据,查看生成的电子病历并关注自身健康信息。此外,移动健康医疗系统结合线上线下模式,可分级查找医生、健康咨询和线上开药等。如图 1所示。
|
Download:
|
|
图 1 移动健康医疗推荐系统框图 Fig. 1 Structure diagram of mobile health care recommendation system |
|
移动健康医疗系统内有大量的健康资讯,通过分析用户的健康数据以及曾经查看的历史纪录,为每一个用户进行个性化信息精准推荐服务。首先通过可穿戴设备采集人体健康数据,在手机设备中对数据可视化。手机设备通过移动网络或因特网将数据发送至系统的大数据中心。服务器分析用户健康数据,抽取出用户当前所关注的健康类别,搭建多层二分网络的“用户-类别”层。其次,在用户使用应用时,服务器会纪录用户浏览帖子时的点击操作。根据这些点击纪录建立“用户-信息”层。当多层二分网络模型生成后,移动健康系统即可对每个用户进行精准健康信息推荐服务。
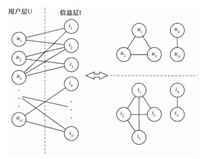
2 二分网络推荐算法基于二分网络的推荐算法把用户和信息看作抽象节点,利用用户和信息之间是否感兴趣建立关系网络。如果用户和信息之间有点击或存在感兴趣行为,则连接这2个节点。当仅考虑一个节点层时,内部节点一定会存在某种对应关系,即有些节点是相互连通的,但有些节点却不能通过其他节点互相连通。这样可以将连通的节点合并成一个独立的节点块。显然,在预测节点的置信度时,本质上是对各个节点块内的初始置信度进行重分配。如图 2所示。
|
Download:
|
|
图 2 用户-信息节点二分图 Fig. 2 Bipartite network of "user-information" |
|
当对用户um进行推荐时,首先根据用户um和信息层I中节点的评分关系,对每一信息节点进行置信度初始化。其次根据二分网络中各个节点的连接关系进行置信传播。最终在置信度重分配后,得到每个节点的预测结果,并向用户um推荐他未阅读的信息中置信度最高的N个信息。
文献[5]提出基于二分网络投影的推荐算法。在协同过滤算法中,经常把数据以用户-信息关系矩阵的形式表现出来,由此关系矩阵,可建立一个二分图,即Graph={U, I, R},集合Graph是图的总称,内部包含用户节点U={u1, u2, …, uM},信息节点I={i1, i2, …, iN},连接2个节点的边R={r11, r12, …, rmn, …rMN}, 其中rij∈0或1,如果rij=1则连接2个节点,反之则不连接。令deg (in)表示in节点的度。设对二分网络中的用户ui进行推荐,需进行以下几个计算步骤:
1)根据评分Ri={ri1, ri2, …, rin, …riN}进行置信度初始化,公式如下:
| $ {{\hat r}_{in}} = {r_{im}}. $ | (1) |
此时信息节点I={i1, i2, …, iN}上的每一个节点都对应一个
2)根据I中每个节点的度进行置信传播,先从信息节点传播到用户节点,公式如下:
| $ {{\hat r}_{im}} = \sum\limits_{{r_{mn}} \in R} {\left( {\frac{{{r_{mn}}}}{{\deg ({i_n})}}{{\hat r}_{in}}} \right)}, $ | (2) |
其中,m∈[1, M]。
在用户层得到用户ui的置信度后,再从用户节点传播到信息节点,完成置信流动并得到用户ui对所有信息的预测值,公式如下:
| $ r{{\hat '}_{in}} = \sum\limits_{{r_{mn}} \in R} {\left( {\frac{{{r_{mn}}}}{{\deg ({u_m})}}{{\hat r}_{im}}} \right)} . $ | (3) |
将(2)、(3)式合并,最终得到对用户ui的每个信息预测值为
| $ \begin{array}{l} r{{\hat '}_{in}} = \sum\limits_{{r_{mn}} \in R} {\left( {\frac{{{r_{mn}}}}{{\deg ({u_m})}}\sum\limits_{{r_{mn}} \in R} {\left( {\frac{{{r_{mn}}}}{{\deg ({i_n})}}{{\hat r}_{in}}} \right)} } \right)} \\ \;\;\;\;\; = \;\sum\limits_{{r_{mn}} \in R} {\sum\limits_{{r_{mn}} \in R} {\left( {\frac{{{r_{mn}}}}{{\deg ({u_m})}}\frac{{{r_{mn}}}}{{\deg ({i_n})}}} \right)} } {{\hat r}_{in}}, \end{array} $ | (4) |
其中:R={r11, r12, …, rmn, …rMN}, n∈[1, N], m∈[1, M]。
预测完用户ui所有信息的置信度后,向用户ui推荐其没看过的信息中置信度最高的前N个,完成最终的推荐。但现实中,用户信息的关系矩阵是一个稀疏矩阵,使得置信度在单独的用户-信息二分网络中不能充分地分配。
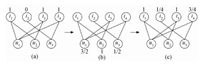
假设有3个用户、4个信息,用户和信息之间的关系给定,现要对u1进行推荐,则置信度流动过程如图 3所示。
|
Download:
|
|
图 3 置信传播例子 Fig. 3 Example of confidence propagation |
|
首先对用户u1的4个信息进行置信度初始化,分别为[1, 0, 1, 1];通过第一次置信传播,置信度传播到用户节点,分别为
然而,二分网络推荐算法的用户评价标准并没有考虑用户“不感兴趣”信息这一方面。文献[6]在传统二分网络的基础上,重新修改了置信度初始化方案,通过计算用户的平均打分程度来衡量“感兴趣”与“不感兴趣”,引入负资源,提高了推荐的准确率与效率。
3 移动健康医疗系统的多层二分网络推荐算法基于多层二分网络的推荐算法(multi-bipartite network projection,MNP)相比传统的二分网络推荐算法,具有以下改进:
1)在二分网络的基础上引入负置信度对节点置信度进行初始化,将用户评价标准扩展为“感兴趣”、“不感兴趣”和“未知”3个方面,提高了推荐算法性能。
2)根据用户喜欢的信息类别,在原有的“用户-信息”网络上添加了新的一层“用户-类别”网络,使置信度在多层网络中可迭代传播,直至收敛。
3.1 初始化过程在实际中,用户和信息之间关系矩阵R中的rij并不是以二值形式“0”或“1”存储,它通常是一个有权值的评分0~5。文献[7]将该评分用固定阈值二值化。但不同的人对信息的评判标准是不同的,喜好标准仅仅用“感兴趣”和“未知”来评价是有局限性的。针对该情况,文献[6]通过引入负置信度的方式,对该关系矩阵进行量化,即将喜好标准扩展为“感兴趣”、“不感兴趣”和“未知”3个方面。针对不同用户,评判标准也不同。本文通过加入并改进负置信度的方式提升算法性能。
根据用户ui的评分集合Ri={ri1, ri2, …, rij, …riN},其中rij∈[0, 5],构建二分网络,初始化过程如下:
| $ {{\hat r}_{in}} = \left\{ \begin{array}{l} -({r_{i{\rm{MAX}}}}-{r_{in}}), \;\;\;\;\;{r_{in}} < {{\bar r}_i}, \\ {r_{in}}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{r_{in}} \ge \bar r. \end{array} \right. $ | (5) |
其中:
连接用户和信息时,用评分是否高于该用户的平均评分
二分网络中的置信传播算法的计算过程如图 3所示,然而,在计算用户u2的信息i2的预测值时,无论怎么初始化置信度,最终结果都是“0”。这是因为i2的置信度只能由u3传播过来,但u3又与u2完全独立,即得不到任何置信度。
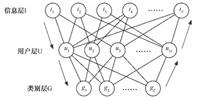
针对这种情况,本文在原有的二分网络的基础上,提出一种多层二分网络算法,即增加一层类别层G。此时图模型变为Graph={U, I, G, RUI, RUG},类别层G={g1, g2, …, gK}表示所有类型节点;RUI表示“用户-信息”二分网络,
| $ {r_{ik}} = \left\{ \begin{array}{l} {r_{ik}} + 1, {{\hat r}_{in}} > 0且{g_k} \in ({i_n}的类别), \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0, 否则. \end{array} \right. $ | (6) |
多层二分网络如图 4所示。
|
Download:
|
|
图 4 多层二分网络模型 Fig. 4 Model of multi-bipartite network |
|
当置信度流动到类别层,便能减少节点得不到置信度的现象,同时该方法使得置信度又在类别层传播了一次,相比原始的模型,预测的准确度明显增加。
接下来,将上述模型写成矩阵的形式,即最终用户ui在所有信息I上的置信度为
| $ \boldsymbol{\hat I}' = \boldsymbol{I}' \cdot {\boldsymbol{M}_{IU}} \cdot {\boldsymbol{M}_{UG}} \cdot {\boldsymbol{M}_{GU}} \cdot {\boldsymbol{M}_{UI}}. $ | (7) |
其中:
| $ \begin{array}{l} \boldsymbol{\hat I}' = \{ r{{\hat '}_1}, r{{\hat '}_2}, r{{\hat '}_3}, \cdots, r{{\hat '}_n}\} \in {\mathbb{R}^N};\\ \boldsymbol{\hat I} = \{ {{\hat r}_1}, {{\hat r}_2}, {{\hat r}_3}, \cdots, {{\hat r}_n}\} \in {\mathbb{R}^N};\\ {\boldsymbol{M}_{IU}} = \left( \begin{array}{l} \frac{1}{{\sum\nolimits_{m = 1}^M {{r_{m1}}} }}{\boldsymbol{R}_{U{i_1}}}\\ \frac{1}{{\sum\nolimits_{m = 1}^M {{r_{m2}}} }}{\boldsymbol{R}_{U{i_2}}}\\ \;\;\;\;\;\; \vdots \\ \frac{1}{{\sum\nolimits_{m = 1}^M {{r_{mN}}} }}{\boldsymbol{R}_{U{i_N}}} \end{array} \right) \in {\mathbb{R}^{N \times M}}, \\ {\boldsymbol{M}_{UI}} = \left( \begin{array}{l} \frac{1}{{\sum\nolimits_{n = 1}^N {{r_{1n}}} }}{\boldsymbol{R}_{{u_1}I}}\\ \frac{1}{{\sum\nolimits_{n = 1}^N {{r_{2n}}} }}{\boldsymbol{R}_{{u_2}I}}\\ \;\;\;\;\;\; \vdots \\ \frac{1}{{\sum\nolimits_{n = 1}^N {{r_{Mn}}} }}{\boldsymbol{R}_{{u_M}I}} \end{array} \right) \in {\mathbb{R}^{M \times N}}, \\ {\boldsymbol{M}_{UG}} = \left( \begin{array}{l} \frac{1}{{\sum\nolimits_{k = 1}^K {{r_{1k}}} }}{\boldsymbol{R}_{{u_1}G}}\\ \frac{1}{{\sum\nolimits_{k = 1}^K {{r_{2k}}} }}{\boldsymbol{R}_{{u_2}G}}\\ \;\;\;\;\;\; \vdots \\ \frac{1}{{\sum\nolimits_{k = 1}^K {{r_{Mk}}} }}{\boldsymbol{R}_{{u_M}G}} \end{array} \right) \in {\mathbb{R}^{M \times K}}, \\ {\boldsymbol{M}_{GU}} = \left( \begin{array}{l} \frac{1}{{\sum\nolimits_{m = 1}^M {{r_{m1}}} }}{\boldsymbol{R}_{U{g_1}}}\\ \frac{1}{{\sum\nolimits_{m = 1}^M {{r_{m2}}} }}{\boldsymbol{R}_{U{g_2}}}\\ \;\;\;\;\;\; \vdots \\ \frac{1}{{\sum\nolimits_{m = 1}^M {{r_{mK}}} }}{\boldsymbol{R}_{U{g_K}}} \end{array} \right) \in {\mathbb{R}^{K \times M}}. \end{array} $ |
以上的置信传播仅仅是来回传播了一次,但一次往往不能使置信度流动至收敛,所以本文采用迭代的思想,将本次置信度初值更新为上一次传播回来的置信度,当前后两次迭代计算出来的结果差值变化幅度很小或超出迭代最大次数时,终止迭代。
算法:多层二分网络迭代算法
需要:
用户-信息投影矩阵MIU、MUI;
用户-类别投影矩阵MGU、MUG;
用户置信度初始向量
理论差值最大值ε;
迭代最大次数N
1: n=1
2: while |error′n-error′n-1|>ε do
3: if n>N
4:break
5: end if
6:
7: error′n=
8: n=n+1
9: end while
3.3 冷启动问题处理当要对一个新加入的用户uM+1进行推荐时,由于uM+1在用户-信息关系矩阵RUI没有与任何信息节点相连接,仅仅通过传统二分网络推荐算法是不能对该用户进行推荐的。但在多层二分网络中,可以通过询问或者分析用户的基本资料,提取出其感兴趣的类别,获得用户-类别关系矩阵RUG,然后初始化类别层的各个节点置信度并开始置信度传播,通过以上的多层二分网络推荐算法得到最终对新用户uM+1的推荐。
4 仿真实验与结果分析 4.1 实验数据集和测评标准为验证面向移动医疗的多层二分网络推荐算法的有效性,采用GroupLens提供的MovieLens数据[14]和图 1所示的移动健康医疗推荐系统进行仿真实验。数据集分为训练集合与测试集合,保证训练数据和测试数据不相交。通过分析训练集合的数据建立多层二分网络模型,对测试集合中用户的信息值进行预测,并和真实值进行对比,测评算法的有效性。本仿真实验使用两种测评方法[15],验证了本文算法的有效性。
1)准确率-召回率(precision-recall,PR)曲线是测评推荐系统很常用的一种方法。P是指准确率,表示算法的推荐结果中正好出现在实际的推荐列表中的信息占预测推荐列表中总信息的百分比;R是指召回率,表示算法的推荐结果中正好出现在实际的推荐列表中的信息占实际推荐列表总信息的百分比。公式分别如下:
| $ \text{precison}=\frac{\sum\nolimits_{u}{\left| R(u)\cap T(u) \right|}}{\sum\nolimits_{u}{\left| R(u) \right|}}, $ | (8) |
| $ \text{Recall}=\frac{\sum\nolimits_{u}{\left| R(u)\cap T(u) \right|}}{\sum\nolimits_{u}{\left| T(u) \right|}}. $ | (9) |
其中:R(u)为用户u推荐的N个信息集合;T(u)为用户u在测试集上实际喜欢的信息集合,本文中即为实际评分不低于用户平均评分的信息集合。
计算不同N下准确率和召回率的值后,可以画出PR曲线,曲线越靠近(1, 1)点说明算法越好。
2)观察者操作特征(receiver operating characteristic,ROC)曲线是用于测评二值分类器的一种很有效的方法,其横轴是由分类器得到的负样本中实际负样本误分的概率,由假阳性率(false positive rate,FPR)表示;纵轴是由分类器得到的正样本中实际正样本对分的概率,由真阳性率(true positive rate,TPR)表示,公式分别如下:
| $ \text{FPR}=\frac{FP}{N};\text{TPR}=\frac{TP}{P}. $ | (10) |
其中:N, P分别表示由分类器所得到的负样本数和正样本数,TP和FP分别表示真阳性数和假阳性数。
在得到推荐算法的预测结果后,对预测值由高到低排序,遍历所有排序位置,高于此位置的预测值分为正样本,反之分为负样本,计算FPR和TPR并画出曲线。显然,二值分类器理论预测准确率下界为50%,对应(0, 0)和(1, 1)的对角线。得到ROC曲线后,计算曲线下面积(area under curve,AUC)值,该值越高说明效果越好。
4.2 实验结果与分析为验证多层二分网络推荐算法具有更准确的推荐效果,本文对比了基本二分网络算法(BNP)[5]、改进二分网络算法(bipartite network projection improved,BNPI)[6]以及本文提出的多层二分网络推荐算法(MNP),通过4.1中描述的测评方式进行对比。
3种算法的PR曲线如图 5所示,3条曲线分别为基本二分网络算法、改进型二分网络算法和多层二分网络推荐算法。BNP在低召回率下准确度和MNP很接近,但随着召回率的增加,BNP的准确率急剧下降,明显低于MNP的准确率。在召回率为20%时,MNP的准确率相比BNP高出8.14%。BNPI算法的性能也是随着召回率的增加,准确率明显优于BNP,但却不如MNP。综上所述,MNP的推荐效果优于其他两种算法。
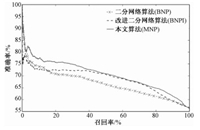
|
Download:
|
|
图 5 3种推荐算法的PR曲线对比图 Fig. 5 Comparison of PR curves among the three algorithms |
|
3种推荐算法的ROC曲线如图 6所示,多层二分网络推荐算法仍然优于其他2个算法。同时对比计算出AUC值,如表 1所示,MNP算法的推荐效果更优。
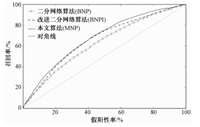
|
Download:
|
|
图 6 3种推荐算法的ROC曲线对比图 Fig. 6 Comparison of ROC curves among the three algorithms |
|
|
|
表 1 3种推荐算法的AUC值 Table 1 Comparison of AUC values among the three algorithms |
多层二分网络迭代算法在冷启动上面具有更好的推荐效果。本文在训练数据中删除了用户u1的评分数据,通过分析用户u1的评分筛选出他感兴趣的3个信息类别。本文采用2种方式对新用户u1进行推荐,一是通过所筛选的信息类别进行推荐(Genre);二是通过多层二分网络进行推荐(MNP),计算AUC值。
在冷启动问题上,MNP以类别层为桥梁,成功地将新用户与多层二分网络融合,既从内容上对数据进行分析,也从集体智慧的角度对新用户进行推荐。如表 2和图 7所示,多层二分网络推荐算法在冷启动情况下的推荐能力优于传统的根据类别的推荐方法。
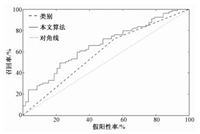
|
Download:
|
|
图 7 2种推荐算法在冷启动时的ROC曲线 Fig. 7 Comparison of cold-start ROC curves between the two algorithms |
|
|
|
表 2 2种推荐算法在冷启动情况下的AUC值 Table 2 Comparison of cold-start AUC values between the two algorithms |
为使移动健康医疗系统能够对用户进行精准医疗信息服务,本文在传统二分网络推荐算法的基础上,提出一种多层二分网络推荐算法。该算法在二分网络的基础上引入负置信度对节点置信度进行初始化,将用户评价标准扩展为“感兴趣”、“不感兴趣”和“未知”3个方面,提高了推荐算法性能;同时,算法根据用户感兴趣的信息类别,在原有的“用户-信息”网络上添加新的一层“用户-类别”网络,使置信度在多层网络中可迭代传播,实现精准医疗推荐。实验结果表明,多层二分网络推荐算法提高了推荐系统的准确率。同时,将算法成功应用到移动健康医疗系统当中,提升了现有医疗资源的使用效率。
| [1] | Deshpande M, Karypis G. Item-based top-N, recommendation algorithms[J]. ACM Transactions on Information Systems , 2014, 22 (1) :143–177. |
| [2] | Javari A, Gharibshah J, Jalili M. Recommender systems based on collaborative filtering and resource allocation[J]. Social Network Analysis & Mining , 2014, 4 (1) :1–11. |
| [3] | BalabanovićM, Shoham Y. Fab:content-based, collaborative recommendation[J]. Communications of the ACM , 1997, 40 (3) :66–72. DOI:10.1145/245108.245124 |
| [4] | Pazzani M J, Billsus D. Content-based recommendation systems[C]//Springer-Verlag, LNCS, 2007, 4321:325-341. |
| [5] | Zhou T, Ren J, MEDO Matuo, et al. Bipartite network projection and personal recommendation[J]. Physical Review E , 2007, 76 (4) :70–80. |
| [6] | Yin F, Zhao X, Zhang X, et al. Improving accuracy and scalability of personal recommendation based on bipartite network projection[J]. Mathematical Problems in Engineering , 2014 :823749. |
| [7] | Zhang X M, Jiang S Y. Personalized recommendation algorithm based on weighted bipartite network[J]. Journal of Computer Applications , 2012, 32 (3) :654–653. |
| [8] | Guo Q, Song W J, Hou L, et al. Effect of the time window on the heat-conduction information filtering model[J]. Physica A Statistical Mechanics & Its Applications , 2014, 401 (5) :15–21. |
| [9] | Fouss F, Pirotte A, Renders J M, et al. Random-walk computation of similarities between nodes of a graph with application to collaborative recommendation[J]. Knowledge & Data Engineering IEEE Transactions on , 2007, 19 (3) :355–369. |
| [10] | Sadja A, Tang J, Mihalov B, et al. System and method for providing recommendations to a user in a viewing social network:US, US 20120117167 A1. 2012. |
| [11] | Koren Y, Bell R, Volinsky C. Matrix factorization techniques for recommender systems[J]. IEEE Computer , 2009, 42 (8) :30–37. DOI:10.1109/MC.2009.263 |
| [12] | Jamali M, Ester M. A transitivity aware matrix factorization model for recommendation in social networks[C]//IJCAI 2011, Proceedings of the International Joint Conference on Artificial Intelligence. Barcelona, Catalonia, Spain. 2011:2644-2649. |
| [13] | Schein A I, Popescul A, Ungar L H, et al. Methods and metrics for cold-start recommendations[C]//International ACM SIGIR Conference on Research and Development in Information Retrieval. ACM, 2002:253-260. |
| [14] | Miller B N, Albert I, Lam S K, et al. MovieLens unplugged:experiences with an occasionally connected recommender system[C]//International Conference on Intelligent User Interfaces. ACM, 2003:263-266. |
| [15] | Davis J, Goadrich M. The relationship between precision-recall and ROC curves[C]//Proceedings of the 23rd international conference on Machine learning. ACM, 2010:233-240. |
 2017, Vol. 34
2017, Vol. 34 


