合成孔径雷达具有全天时、全天候成像特点,目前已被广泛应用于军事侦察及民用遥感领域。随着星载SAR系统不断向高分辨率、宽测绘带、多极化方式等方向发展,为满足SAR原始数据实时下传需求,在星上需采用性能更高的SAR原始数据压缩方法降低数据传输速率,以满足通信带宽的要求。
自20世纪80年代起,学者们提出了为数众多的SAR原始数据压缩算法,典型的有:适应于SAR原始数据统计特性的标量量化算法[1]以及利用SAR原始数据内在相关性的矢量量化算法[2]。与时域的量化编码算法相比较,变换域压缩方法具有更好的性能,典型的算法有:基于小波变换的方法[3]、子带编码方法[4]、基于FFT变换的编码方法[5]。变换域压缩方法具有较高的复杂度,目前还没有在星载SAR系统中得到实际应用。除上述方法之外,其他SAR原始数据压缩方法如网格编码量化(TCQ)[6-7]、预测编码[8-9]、压缩感知[10-11]以及熵限制量化方法(ECBAQ)[12]也被应用于SAR原始数据压缩的研究,分别具有不同的优缺点。在目前已出现的SAR原始数据压缩方法中,分块自适应量化(BAQ)算法[13]因其硬件实现的简单性,目前已被用于Magellan SAR,ENVISAT A-SAR,TerraSAR-X和Radarsat-2等多部星载SAR系统中。
近年来,BAQ算法在实际应用时也不断被优化完善,在TerraSAR-X系统[14-17]中,使用具有不同比特率的BAQ量化器提高总体压缩性能,编码器依据世界各地的地物散射特性进行不同比特率BAQ的切换。在欧空局的哨兵1号(Sentinel-1)[18-22]任务中,信号与热噪声比(STNR, signal-to-thermal-noise ratio)被用于实现不同比特率BAQ的自适应切换。作为BAQ算法的扩展,FDBAQ算法(flexible dynamic block adaptive quantizer)在保持BAQ算法简单性的同时能得到更好的压缩性能,该算法能够依据接收信号的功率不同自适应选择最优量化器。FDBAQ量化器利用SAR原始数据分块的几百个采样点测量局部杂波功率,该量化器需要NESZ (noise equivalent sigma zero)[18]的先验知识,但是NESZ不能在线测量,只能通过地面测试设备估计得到,对FDBAQ的优化需要信号统计特性及热噪声功率两方面的先验知识。SA-FBQ[23]通过采用适应于SAR原始数据局部统计特性的量化器组进一步扩展FDBAQ的概念。FDBAQ和SA-FBQ的主要缺陷在于:都需要事先测定地球上不同区域的地物散射特性的先验知识,地物散射特性的测定是通过之前发射的SAR卫星数据得到的,在缺乏先验知识的情况下,只能通过压缩算法本身的优化提高数据压缩性能。
虽然SAR原始数据概率统计上符合高斯分布,但是由于SAR系统天线方向图调制及地物散射特性的不同,实行分块编码时,每个分块数据的回波信号功率是变化的。使用BAQ算法做原始数据量化时,如果成像场景是均匀的,则固定比特率BAQ是最优选择;但是对于非均匀区域,应该选择可变比特率量化器以适应地物散射特性的变化,即信号功率大的数据分块应该采用高比特率量化器,反之则采用低比特率量化器。
本文在上述已有工作基础上,提出一种可变比特率BAQ算法,在保持平均比特率一定的前提下,针对不同的数据分块可自适应选择量化比特率。与FDBAQ和SA-FBQ相比,本文的比特率选择机制基于分块数据的信号功率大小,可自适应选择不同比特率的量化器,无需成像区域地物散射特性等先验知识。与传统BAQ算法相比,新方法能够明显提高数据量化信噪比并降低SAR复图像相位误差,而运算复杂度增加很小。除此之外,新方法与固定比特率BAQ算法相比,可以实现分数比特率,适应于不同通信带宽的数据传输需要,增加了SAR原始数据实时传输的灵活性。
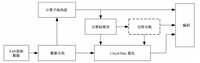
1 算法基本原理经典的BAQ算法[13]利用SAR原始数据统计特性符合高斯分布的特点,对数据进行分块处理,该方法首先计算分块数据的幅度均值,并将幅度均值映射为标准差,对每一子块数据利用标准差进行归一化,之后应用Lloyd-Max量化器进行量化编码。图 1中虚线框部分是本文算法不同于传统BAQ算法的地方,比特分配机制使得针对每一子块的BAQ量化不再是固定比特率量化,即在平均比特率一定的前提下,每个子块量化比特率是可变的。本文算法的基本思想是:对于SAR原始数据各子块,标准差反映了子块内信号功率的强弱,因此可根据子块数据标准差不同,在多个子块之间进行比特分配。标准差大的子块分配较多的量化比特数,反之则分配较少的比特,达到总体上提高压缩性能的目的。
|
Download:
|
|
图 1 自适应比特分配BAQ算法原理框图 Fig. 1 Block diagram of the proposed compression algorithm |
|
比特分配的基本思想是对标准偏差较大的子块分配较多的量化比特数,而对标准偏差较小的子块分配较少的比特数,使得在总比特数一定的条件下,总的量化误差最小。
设p(x)为随机信源X的概率密度函数,则均方量化误差为
| $ d(R) = E[{(X-\tilde X)^2}], $ | (1) |
其中:X表示待量化信号,
| $ R(D) = \frac{1}{2}{\log _2}\left( {\frac{{{\sigma ^2}}}{D}} \right). $ | (2) |
设SAR原始数据编码时一次处理的子块个数为M,则所有子块数据量化的平均失真为
| $ {D_T}({R_T}) = \frac{1}{M}\sum\limits_{n = 0}^{M-1} {{d_n}({R_n}).} $ | (3) |
由式(2)可以求出
| $ D = {\sigma ^2} \times {4^{-R}}, $ | (4) |
代入式(3)中,可得
| $ {D_T}({R_T}) = \frac{1}{M}\sum\limits_{n = 0}^{M-1} {\sigma _n^2 \times {4^{-{R_n}}}.} $ | (5) |
则最优比特分配问题可描述为:当所有子块数据量化的平均比特率
| $ \begin{array}{l} \mathop {\arg \min }\limits_{{R_n}} J = \mathop {\arg \min }\limits_{{R_n}} [\frac{1}{M}\sum\limits_{n = 0}^{M-1} {\sigma _n^2 \times {4^{-{R_n}}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\lambda (\frac{1}{M}\sum\limits_{n = 0}^{M-1} {{R_n}} - {R_T})]. \end{array} $ | (6) |
利用拉格朗日乘数法求解上述最小化问题,需求解如下方程组:
| $ \left\{ \begin{array}{l} \frac{{\partial J}}{{\partial {R_n}}} = \sigma _n^2(-{\rm{In}}4){4^{-{R_n}}} + \lambda = 0, n = 0, 1, \cdots, M-1, \\ \frac{{\partial J}}{{\partial \lambda }} = \frac{1}{M}\sum\limits_{n = 0}^{M - 1} {{R_n}} - {R_T} \end{array} \right. $ | (7) |
求解方程组(7),可得
| $ {R_n} = {R_T} + \frac{1}{2}[{\rm{lo}}{{\rm{g}}_2}\sigma _n^2-\sum\limits_{n = 0}^{M-1} {{{\log }_2}\sigma _n^2}]. $ | (8) |
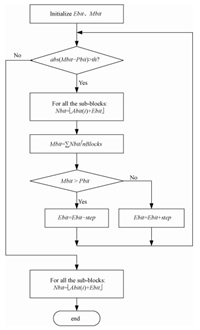
求得的Rn为分数比特率,为适应BAQ量化器定长编码的需要,需要对其进行四舍五入取整。分数比特率经四舍五入取整后求平均,与预设的平均比特率存在误差。为使平均比特率更接近预设值,采用如图 2所示的比特误差控制算法得到接近预设值的比特率。在图 2中,定义如下符号:
|
Download:
|
|
图 2 平均比特率控制算法流程图 Fig. 2 Flow chart of the mean bit rate control algorithm |
|
· Ebit:比特数误差;
· Mbit:各子块的平均比特数;
· Pbit:预设的各分块平均比特数;
· Abit:针对某一子块由式(8)计算得到的比特数;
· Nbit:针对某一子块已分配的比特数;
· th:Mbit与Pbit的误差阈值。
3 实验结果与分析由于无法得到星载SAR系统实时获取的无失真SAR原始数据,本文采用中国科学院电子学研究所某机载SAR获取的2块原始数据作为实验数据。数据经A/D量化为8 bit有符号数据,地物类型为城市郊区,实验结果对于星载SAR原始数据压缩具有重要参考意义。使用C++语言编写原始数据压缩与解压缩程序,分别采用自适应比特分配BAQ算法(A-BAQ)和传统BAQ算法做压缩实验,并定量计算其相应的性能指标,实验结果分别如表 1、表 2所示。在A-BAQ算法中,由于所有子块使用BAQ量化时的最低比特率限定为1 bit (BAQ量化器定长编码的需要),所以为体现各子块间比特分配效果,A-BAQ算法平均比特率的最小值应大于1 bit,本文设定为1.5,而最大值设定为3.0。原始数据域采用量化信噪比和平均相位误差来衡量压缩性能,信噪比定义如下:
| $ {\rm{SNR}} = 101{\rm{g}}(\frac{s}{\varepsilon }), $ | (9) |
|
|
表 1 SAR原始数据域评价结果 Table 1 Compression performance in SAR raw data domain |
|
|
表 2 SAR图像域评价结果 Table 2 Compression performance in SAR image domain |
其中:
| $ {\rm{MPE}} = \frac{1}{{MN}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {\left| {{\phi _0}(i, j)-{\phi _1}(i, j)} \right|} }, $ | (10) |
其中:Φ0(i, j)为原始数据相位;Φ1(i, j)为解压重建数据相位。其单位均为弧度。
采用峰值信噪比评价SAR图像质量,式(9)中如果取s为峰值信号的功率,则峰值信噪比定义如下所示(对于16位存储的SAR幅度图像,信号峰值取为65 535):
| $ {\rm{PSNR}} = 10 \times {\rm{lg}}\left( {\frac{{{s_{\max }}}}{\varepsilon }} \right). $ | (11) |
由表 1、表 2可以看出,无论是SAR原始数据域还是图像域,相同比特率前提下,A-BAQ算法与BAQ算法相比,均具有较高的信噪比和较低的相位误差。当比特率为2.0时,数据域信噪比提高约1.7 dB,图像域信噪比提高约3.6 dB,原始数据相位误差降低约0.03 rad,复图像相位误差降低约0.17 rad。尤其值得一提的是,A-BAQ算法在图像域性能提高更为明显,进一步说明通过在子块数据之间进行比特分配,可以使强散射区域得到更多的编码比特数,有助于提高SAR图像质量,且较好地保持了相位信息。A-BAQ算法使用比特分配机制可实现分数比特率,在实际应用时可根据数传速率不同,提供多种比特率选择方式,增加了应用的灵活性。A-BAQ算法与目前国际上最先进的FDBAQ算法(应用于ESA的Sentinel-1任务中)和SA-BAQ算法相比,无需先验知识,而压缩性能的提高与之相当,SAR系统实现复杂度增加很少,具有较高的实用性和普适性。
分别对未经压缩的原始数据以及本文算法在不同比特率时的解压缩数据进行成像,图 3给出成像的结果,所有图像均使用16 bit无符号存储,符号CR表示压缩比。

|
Download:
|
|
图 3 解压缩数据成像结果与原始图像的比较 Fig. 3 Imaging results for SAR raw data and decompression data |
|
图 3所示4幅图像的对比结果表明,A-BAQ算法在压缩比为5.33时依然能够得到很好的图像质量,与压缩比为4的BAQ算法得到的SAR图像质量相当。说明通过比特分配机制能够有效提高SAR原始数据压缩性能,可为星载SAR系统实时数据压缩提供更加灵活的选择。
4 结束语针对SAR原始数据实时编码传输应用,本文在传统BAQ算法基础上,依据数据分块信号功率不同,在数据分块之间进行自适应比特分配以提高压缩性能,在保持平均比特率一定的前提下,针对不同的数据分块可自适应选择比特率不同的BAQ量化器。本文同时给出比特分配的计算方法,与目前星载SAR系统在用的先进SAR原始数据量化器相比,本文的比特分配机制无需成像区域地物散射特性等先验知识,系统实现较为简单。实验结果表明,新方法能够明显提高SAR原始数据量化信噪比并降低SAR复图像相位误差,而运算复杂度增加很小。分数比特率的实现也为SAR原始数据实时传输提供了更加灵活的选择。工程实现时,本文方法只需要在传统BAQ方法基础上增加比特分配环节,硬软件改动很小,具有重要的工程应用价值。
| [1] | Koren Y, Yavneh I, Spira A. A multigrid approach to the scalar quantization problem[J]. IEEE Trans on Geosci and Remote Sensing , 2005, 51 (8) :2993–2998. |
| [2] | 祁海明, 华斌, 李信. 星载SAR原始数据普适性分块自适应矢量压缩算法[J]. 中国科学:信息科学 , 2012, 42 (2) :206–217. |
| [3] | 潘志刚, 王岩飞. 一种基于小波变换的高倍数SAR原始数据压缩算法[J]. 电子与信息学报 , 2006, 28 (10) :1798–1801. |
| [4] | Pascazio V, Schirinzi G. SAR raw data compression by subband coding[J]. IEEE Trans on Geosci and Remote Sensing , 2003, 41 (5) :964–976. DOI:10.1109/TGRS.2003.811811 |
| [5] | Benz U, Strodl K, Moreria A. A comparison of several algorithms for SAR raw data compression[J]. IEEE Trans on Geosci and Remote Sensing , 1994, 33 (5) :1266–1276. |
| [6] | Elia C D', Poggi G, Verdoliva L. Compression of SAR raw data through range focusing and variable-rate trellis-coded quantization[J]. IEEE Trans on Image Processing , 2001, 10 (9) :1278–1287. DOI:10.1109/83.941852 |
| [7] | Owens J W, Marcellin M W, Hunt B R, et al. Compression of synthetic aperture radar video phase history data using trellis-coded quantization techniques[J]. IEEE Trans on Geosci and Remote Sensing , 1999, 37 (2) :1080–1085. DOI:10.1109/36.752226 |
| [8] | Magli E, Olmo G. Lossy predictive coding of SAR raw data[J]. IEEE Trans on Geosci and Remote Sensing , 2003, 41 (5) :977–987. DOI:10.1109/TGRS.2003.811556 |
| [9] | Ikuma T, Naraghi-Pour M, Lewis T. Predictive quantization of range-focused SAR raw data[J]. IEEE Trans on Geosci and Remote Sensing , 2012, 50 (4) :1340–1348. DOI:10.1109/TGRS.2011.2167236 |
| [10] | Bhattacharya S, Blumensath T, Mulgrew B, et al. Fast encoding of synthetic aperture radar raw data using compressed sensing[C]//IEEE/SP Workshop on Statistical Signal Processing. Madison, US:WI, 2007:448-452. |
| [11] | Chen Y C, Zhang Q, Wang G Z, et al. A novel compressing method of airborne SAR raw data[C]//IEEE International Conference on Signal Processing, Communication & Computing. Kunming:IEEE, 2013:1-5. |
| [12] | Algra T. Data compression for operational SAR missions using entropy-constrained block adaptive quantization[C]//IEEE International Geoscience & Remote Sensing Symposium. Toronto:IEEE, 2002:1135-1138. |
| [13] | Kwok R, Johnson W T K. Block adaptive quantization of Magellan SAR data[J]. IEEE Trans on Geosciences and Remote Sensing , 1989, 27 (4) :375–383. DOI:10.1109/36.29557 |
| [14] | Krieger G, Moreira A, Fiedler H, et al. TanDEM-X:a satellite formation for high-resolution SAR interferometry[J]. IEEE Trans on Geosciences and Remote Sensing , 2007, 45 (11) :3317–3341. DOI:10.1109/TGRS.2007.900693 |
| [15] | Mittermayer J, Younis M, Metzig R, et al. Terra SAR-X system performance characterization and verification[J]. IEEE Trans on Geosciences and Remote Sensing , 2010, 48 (2) :660–676. DOI:10.1109/TGRS.2009.2026742 |
| [16] | Martone M, Brautigam B, Krieger G. Azimuth-switched quantization for SAR systems and performance analysis on TanDEM-X data[J]. IEEE Geosciences and Remote Sensing Letter , 2014, 11 (1) :181–185. DOI:10.1109/LGRS.2013.2251603 |
| [17] | Martone M, Brautigam B, Krieger G. Quantization effects in TanDEM-X Data[J]. IEEE Trans on Geosciences and Remote Sensing , 2015, 53 (2) :583–597. DOI:10.1109/TGRS.2014.2325976 |
| [18] | Attema E, Cafforio C, Gottwald M, et al. Flexible dynamic block adaptive quantization for Sentinel-1 SAR missions[J]. IEEE Geosciences and Remote Sensing Letter , 2010, 7 (4) :766–770. DOI:10.1109/LGRS.2010.2047242 |
| [19] | Snoeij P, Attema E, Guarnieri A M, et al. FDBAQ:a novel encoding scheme for Sentinel-1[C]//IEEE International Geoscience and Remote Sensing Symposium. Cape Town:IEEE, 2009:44-47. |
| [20] | Guccione P, Cafforio C, Guarnieri A M. Optimal block quantization for SAR data[C]//IEEE Radar Conference. Arlington, Virginia:IEEE, 2010:348-353. |
| [21] | Guccione P, D'Aria D, Piantanida R. Sentinel-1 FDBAQ performances:the data compression and estimation tool[C]//Advances in Radar and Remote Sensing. Tyrrhenian:IEEE, 2012:18-25. |
| [22] | Malz E, Scheiber R, Mittermayer J, et al. Sentinel-1 FDBAQ performance validation using TerraSAR-X data[C]//IEEE International Geoscience and Remote Sensing Symposium. Munich:IEEE, 2012:1629-1632. |
| [23] | Guccione P, Guarnieri A M. A space adaptive quantizer for spaceborne SAR[J]. IEEE Trans on Geosciences and Remote Sensing , 2011, 49 (10) :3564–3573. DOI:10.1109/TGRS.2011.2158222 |
 2017, Vol. 34
2017, Vol. 34 


