2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
合成孔径雷达(synthetic aperture radar,SAR)是一种微波主动式相干成像系统,具有全天时、全天候、大测绘带等优势,在遥感物理信息获取、军事态势感知等诸多方面具有不可替代的作用[1-4]。随着硬件和处理技术的发展,SAR图像空间、辐射分辨率不断提升,为目标的精细特征信息提取提供了重要契机。然而,受限于目标场景的复杂性、目标散射特性以及对成像参数如方位角的敏感性等因素,SAR自动目标识别仍然是SAR应用领域最为迫切但又远未实用化的难点问题。
针对SAR目标识别算法的研究已有诸多文献报道[5],代表性的有Novak等[6]提出的模板匹配方法以及Zhao和Principe[7]等提出的基于支持向量机(support vector machine,SVM)的模型匹配方法。前者直接将训练样本作为模板对测试样本进行匹配识别,需要的样本库庞大,只考虑训练样本和测试样本的整体特征相关度;后者是从训练样本特征向量中选择少数支持向量去建立分类模型并依据整体特征对测试样本进行类别判定,其相对模板匹配方法更具实用性。然而,由于SAR目标的方位角敏感问题,此类方法无法自适应地对不同方位角测试样本选择最佳支持,需要对不同方位角的训练样本进行单独处理,识别测试时则需要进行方位角估计,再选择相应方位角范围的训练目标进行识别,因此难以有效推广应用。
近年来,稀疏表示[8-9]逐渐深入应用于图像分析和分类识别等领域。传统的信号表示是利用正交基对测量信号进行展开表示,所以只存在唯一的表示系数。如果以线性相关的冗余基(又称为字典,每个基向量称为原子)代替线性无关的正交基,就存在多组系数可以表示测量信号。表示系数中非零元素的个数用来衡量表示系数的稀疏性,非零元素越少,稀疏性越高,实际参与表示的原子越少,稀疏表示就是求解一组最稀疏的表示系数,亦即从字典中选择最少的一组原子表示观测信号。由于在稀疏表示模型中,相关算法在约束条件下可以优化选择整体或局部特征与待识别样本最相似的一组原子进行表示,因此相对传统识别方法,稀疏表示方法能更好地适应SAR目标识别中的方位角敏感问题。目前已有一定的相关研究,基本方法是首先提取样本图像的图像域和频域等特征,以训练样本特征为原子构建稀疏字典,然后对测试样本特征进行稀疏表示,根据表示结果判别测试样本。代表性的工作有,Thiagarajan等[10]以随机投影方法提取SAR目标特征,使用正交匹配追踪(orthogonal matching pursuit,OMP)算法进行稀疏表示,获得最优90.91%的识别率, 未进行随机投影处理的识别率达到91.43%。刘中杰等[11]利用主成分分析(principal component analysis, PCA)方法对SAR图像域数据进行降维,然后采用稀疏表示方法进行目标分类识别,在未进行预处理的情况下该算法仍能有效地识别目标,比三阶近邻识别(nearest neighbor, NN)算法具有更高的识别率和鲁棒性。程建等[12]以二维图像向量化后的降维数据构建字典,以最小稀疏表示误差以及最大同类稀疏表示系数和为分类准则进行SAR目标识别,在目标方位角状态未知时的识别率(96.41%)高于方位角已知的支撑向量机和近邻识别方法的识别率。齐会娇等[13]对目标图像进行对数变换、滤波、分割和配准等预处理,并直接以目标图像域数据和傅里叶变换后的频域数据为原子构建字典,并引入字典结构优化和联合系数表示的方法进行SAR图像目标识别,对于目标变体取得了较高的识别率,但实验中目标的空频域特征的数据量较大,字典的原子维数过高。
然而,实际中SAR获取的图像往往存在一些干扰(例如,当待识别目标本身或周边存在强散射体时,由于合成孔径处理的影响,强散射体的旁瓣拖尾将叠加于待识别目标之上),导致现有基于图像空间域特征与稀疏表示的SAR目标识别方法的识别率显著下降。
自然界中,很多现象都存在多尺度特性,人眼对真实世界物体的观察及分析往往是在不同尺度关注局部特征而进行的。多尺度分析方法能够更细致地表达目标的根本特征,避免偶发的干扰,提升目标识别的鲁棒性。多尺度分析方法在图像处理和特征分析中也取得了比较好的应用效果。例如Gabor滤波器[14],其通过不同大小和方向的滤波以提取图像中的目标在不同空间位置、方向和频率上的多尺度特征。由于上述特征从图像的局部提取,能够更好地克服SAR图像方位角和噪声等全局干扰以及遮挡等局部干扰对目标识别的影响。本文针对SAR实际应用环境干扰、SAR图像目标各向异性导致的目标自动识别鲁棒性不高问题,利用Gabor滤波器多尺度分析和稀疏表示方法的技术优势,提出基于Gabor多尺度特征和稀疏表示的SAR目标识别方法。
1 Gabor多尺度分析和稀疏表示 1.1 Gabor多尺度分析人眼对于现象和物体的感知是基于多尺度结构的,基于这一基本思想,Witkin[14]提出尺度空间滤波的概念,为尺度空间理论的发展奠定了基础。信号的尺度空间定义如下:设f(X)(X→RN)表示给定的信号,其尺度空间是一族由f导出的信号,表示为
| $ L(X, t) = G(X, t) \otimes f(X), $ | (1) |
式中,G:RN×R+→R是高斯核函数,t∈R+为尺度参量。
目前的多尺度特征主要是指图像的多分辨率特征,与多分辨率数据结构不同。将尺度空间理论引入到图像分析中,在高斯核函数中选择不同大小的尺度参数,对图像进行多尺度滤波,便得到原始图像的多尺度空间。
Gabor滤波器[15]在尺度上具有可调制性,可以对图像进行多尺度分析,已在计算机视觉、纹理分类和图像识别等领域推广应用。Daugman[16]提出二维Gabor滤波器理论, 并阐述了其兼顾空域、频域以及滤波方向得到最佳分辨率的特性。
本文采用文献[16]中的二维Gabor滤波函数作为高斯核函数建立SAR目标图像的多尺度特征空间,形式为
| $ \begin{array}{l} G(X, y, \theta, \lambda ) = \frac{1}{{2{\rm{\pi }}{\sigma _u}{\sigma _v}}}\exp [-\frac{1}{2}(\frac{{{u^2}}}{{\sigma _u^2}}\\ \;\;\;\;\;\;\;\;\;\;\;\; + \frac{{{v^2}}}{{\sigma _v^2}})]\exp [{\rm{i}}(2{\rm{\pi }}\omega u)], \end{array} $ | (2) |
式中:u=xcosθ+ysinθ,v=-xsinθ+ycosθ,θ为滤波方向;σu和σv分别为高斯核函数在u和v方向上的标准差,决定了二维Gabor滤波掩模的大小;ω为用于调制核函数的中心频率。
用具有不同调制频率掩模大小尺度(σu和σv)以及滤波方向尺度(θ)的Gabor滤波器对图像进行卷积运算,得到包含不同空间频率空间位置以及不同方向的局部结构信息的Gabor响应系数。
1.2 稀疏表示广义上的稀疏表示模型的数学表达为
| $ u = D\mathit{\boldsymbol{\alpha }} $ | (3) |
式中:u∈Rm×1为给定的观测信号;D∈Rm×n(m < n)为稀疏字典;α为需求解的表示系数。
D中m < n表示未知数的个数超过方程的个数,因此公式(3)实际上是欠定方程,没有唯一解,即在字典D上没有对u的唯一表示系数。稀疏表示就是基于约束条件u=Dα,求取只有少量非零元素的最稀疏表示系数α。最稀疏解中大部分元素为零,说明实际上只有少量的稀疏解非零元素对应的原子参与观测信号的表示,所以稀疏求解也可以理解为在一定的约束条件下,自适应地选择最优的原子集合来表示观测信号的过程,即解决如下的最优化问题:
| $ \mathit{\boldsymbol{\hat \alpha }} = \arg \min {\left\| \mathit{\boldsymbol{\alpha }} \right\|_p},{\rm{s}}.{\rm{t}}.{\left\| {D\mathit{\boldsymbol{\alpha }} - u} \right\|_2} < \varepsilon . $ | (4) |
式中,‖·‖p表示lp范数。当α的稀疏度与稀疏字典D满足一定条件时,下式(公式(4)的拉格朗日函数形式)中无约束优化目标函数的解就是最稀疏解:
| $ \mathit{\boldsymbol{\hat \alpha }} = \arg \min \left\| {u-D\mathit{\boldsymbol{\alpha }} } \right\|_2^2 +, \lambda {\left\| \mathit{\boldsymbol{\alpha }} \right\|_p} $ | (5) |
式中,‖u-Dα‖22为稀疏表示误差,‖α‖p为稀疏性度量。λ为拉格朗日乘子,在稀疏表示中起着平衡稀疏性和稀疏表示误差的作用:λ值越小,稀疏表示误差项‖u-Dα‖22在目标函数中的权重就越大,所求解的α稀疏度越低;反之,λ越大,表示稀疏性度量的‖α‖p在目标函数中的权重就越大,α的稀疏度越高。
一般情况下对于上述问题的求解有很多求解算法,如:P=0时匹配追踪(matching pursuit, MP)和正交匹配追踪OMP[17]、P=1时贝叶斯稀疏求解算法[18]等。
贝叶斯稀疏求解模型加入了稀疏表示过程中的噪声,模型公式为
| $ u = D\mathit{\boldsymbol{\alpha }} + v $ | (6) |
式中,v为方差为σ2,均值为0的高斯噪声。根据贝叶斯分析理论,u的似然函数为
| $ p(u\left| \mathit{\boldsymbol{\alpha }} \right.) = \frac{1}{{\sqrt {2{\rm{\pi }}{\sigma ^2}} }}\exp \left( {-\frac{1}{{2{\sigma ^2}}}{{\left\| {u-D\mathit{\boldsymbol{\alpha }} } \right\|}^2}} \right). $ | (7) |
为了防止采用最大似然法求解公式(7)可能引起的过学习问题,设待求的稀疏系数α具有先验条件概率分布:
| $ p(u\left| \mathit{\boldsymbol{\gamma }} \right.) = \prod\limits_{i = 1}^n {\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}{\gamma _i}} }}} \exp \left( { - \frac{{u_i^2}}{{2{\gamma _i}}}} \right), $ | (8) |
式中,γ是与表示系数同维数并控制其先验方差的参数,如果求得此中间参数,便容易得到稀疏系数α。根据进行参数估计的最大期望迭代算法原理,优化γ的目标函数为
| $ F(\gamma ) = {\rm{In}}\left| {{\sigma ^2}\mathit{\boldsymbol{I}} + D{\Gamma ^{ - 1}}D} \right| + {\mathit{\boldsymbol{\alpha }} ^{\rm{T}}}\sum\nolimits_\mathit{\boldsymbol{\alpha }} ^{ - 1} \mathit{\boldsymbol{\alpha }} $ | (9) |
式中,Γ=diag (γ-1),I是单位矩阵。通过极小化式(9)(导数为零)求得表示系数α和参数γ第k+1次的迭代式分别为:
| $ {{\boldsymbol{\hat \alpha }}_{(k + 1)}} = \Gamma _{(k)}^{1/2}{(D\Gamma _{(k)}^{1/2})^{ - 1}}u, $ | (10) |
| $ {\boldsymbol{\hat \gamma }_{(k + 1)}} = {\rm{diag}}({\boldsymbol{\hat \alpha }_{(k)}}\boldsymbol{\hat \alpha }_{(k)}^{\rm{T}} + (I - \Gamma _{(k)}^{1/2}{(D\Gamma _{(k)}^{1/2})^{ - 1}}D){\Gamma _{(k)}}). $ | (11) |
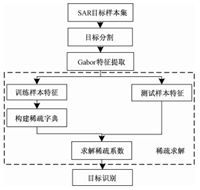
本文方法包括目标分割、Gabor特征提取、稀疏求解以及目标识别4个步骤,图 1是本文方法的流程框图。
|
Download:
|
|
图 1 算法流程图 Fig. 1 Algorithm flowchart |
|
在实际目标图像中,目标区域往往只占据图像的小部分面积, 而背景区域所占面积较大,如果不进行目标分割,其他区域的特征会“淹没”目标区域的特征,并且地面目标所处背景杂波具有多样性。因此,需要首先将目标从图像杂波背景中分离出来,步骤如下:
1)采用马尔科夫方法[19-20]对目标数据集中的每一幅图像进行目标分割;
2)对分割出的区域进行开闭运算处理以剔除分割误差的干扰;
3)保留图像目标区域,将背景区域灰度赋值为常量值,输出目标分割图像。
2.2 Gabor特征提取本文采用的特征提取滤波器组示意图如图 2所示。

|
Download:
|
|
图 2 多尺度Gabor滤波器组 Fig. 2 Gabor filter bank with multiple scales |
|
Gabor多尺度特征提取的具体步骤如下:
1)根据式(1),以不同尺度的Gabor滤波器为高斯核函数,对目标分割图像进行多尺度滤波,获得图像的S幅特征图像序列(S=s×d,s表示掩模大小尺度的尺度数,d表示滤波方向尺度θ的尺度数)。
2)特征图像序列组合成目标的多尺度特征图像,并将此图像以逐列拼接方式转化为一维特征向量。采用主分量变换对目标特征数据降维(可选)。
3)对所有特征数据进行归一化处理(抑制过大或过小的特征的影响)。
2.3 稀疏求解1)将样本特征分为训练集和待识别测试集,以所有训练样本特征向量为原子组合成稀疏字典,测试样本特征留待识别。
2)本文采用贝叶斯稀疏求解算法来求解测试样本特征向量在稀疏字典上的稀疏系数,具体步骤为按照式(10)和式(11)进行迭代求解,终止条件设定为迭代次数达到阈值和两次迭代式中的稀疏系数之间的平方差小于阈值,满足其中一个条件即终止运算并输出稀疏系数。
2.4 目标识别测试样本在字典上的稀疏表示系数是一个维数与字典原子数相同的一维向量,每个系数元素对应字典中一类样本(原子的类别已知),将表示系数元素按类分开并剔除其中的负值,然后计算l1范数。采用的识别准则如下
| $ \hat i = \arg \max {\left\| {\mathit{\boldsymbol{\alpha }} _i^ + } \right\|_1}, $ | (12) |
式中:i表示类别标号;αi+表示稀疏系数中类i对应的非负系数;
本文采用MSTAR项目组公布的SAR目标图像数据集进行实验,该数据集由BMP-2坦克、BTR-70装甲运兵车以及T-72坦克三类目标的SAR切片图像组成,分辨率为0.3 m×0.3 m,图像大小为128×128。表 1是本文实验选用的训练样本图像和测试样本图像的类别和个数,训练样本图像共计698幅,测试样本图像共计587幅。
|
|
表 1 实验数据集 Table 1 Experimental dataset |
本文设置3组实验,以验证算法的有效性以及分析实验参数对识别结果的影响:1)鲁棒性对比实验,分析本文方法与文献[11]和文献[12]的方法,随干扰强度的变化规律;2)尺度数对识别结果影响的实验,通过增加提取目标特征的尺度数,分析识别率的变化;3)字典规模对识别结果影响的实验,从字典原子数和原子维度两方面考虑,改变字典大小分析识别率的变化。
3.2 鲁棒性对比实验文献[11]算法未经过SAR目标图像的预处理,直接对数据进行PCA特征提取和降维,然后稀疏求解的方法是令式(4)中p=1,采用求解最优化问题的数学规划方法得到稀疏系数进而进行分类判别。文献[12]算法仅对图像进行对数归一化处理,使用PCA特征提取和降维,采用截断牛顿内点法和经典的OMP算法进行稀疏求解,比经过目标分割和PCA特征提取的SVM方法具有更高的识别率。因此,本节实验不仅对比本文算法与文献[11]、文献[12]中算法,而且对比了目标分割处理下的该两种方法分析算法在图像有干扰(干扰方式为强散射中心干扰)情况下的识别性能,亦即对测试样本添加亮纹,从数量和强度上增加干扰强度,进而分析目标识别率下降的程度。
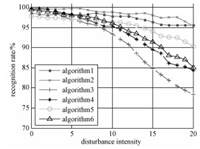
识别率结果如图 3所示,0表示无干扰,1~20表示干扰在亮纹强度和数量上逐步增强,示意图如图 4。表 2是识别时间对比结果,结果表明本文方法的识别时间仅稍多于另两种方法。此外,图 3显示本文方法中的PCA降维处理(降维前数据维数为3 600,降维后维数为30)会导致识别率稍微下降。但由表 2看出,降维处理使所有测试样本的总识别时间大幅减少,在实时性要求高的场合下具有重要意义。可以看出,在干扰程度较低(小于等于4)时,本文方法最优识别率稍低于文献[11]和文献[12]方法的识别率;但随着干扰强度的增加(大于4),文献[11]和文献[12]方法的识别率急剧下降,而本文方法的识别率仅略有下降。强度为15时,文献[11]和文献[12]方法已降到90%以下,而本文方法的识别率仍高达95.7%。此外,目标分割预处理在一定程度上提高文献[11]和文献[12]方法在干扰情况下的识别率,但仍低于本文方法。
|
Download:
|
|
图 3 目标识别率随干扰强度变化趋势 Fig. 3 Target recognition rate variation with disturbance intensity |
|

|
Download:
|
|
图 4 干扰强度示意图 Fig. 4 Diagram of disturbance intensity |
|
|
|
表 2 识别时间 Table 2 Recognition time |
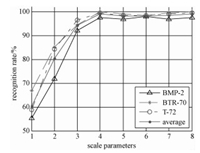
本节研究算法中的尺度参数对识别率的影响,具体如下:参考公式(2),共取8个滤波方向尺度θ=[0, π/8, π/4, 3π/8, π/2, 5π/8, 3π/4, 7π/8],对SAR图像在各个方向上进行Gabor滤波提取特征,识别时选择尺度数从1到8增加,研究识别率随尺度数的变化。图 5是在方向数一定时每类目标的识别率和3类目标平均识别率随尺度数变化的趋势图。当尺度数较小时,平均识别率随着尺度数的增多而提高;当尺度数为4时,平均识别率最高,当尺度数继续增加时,平均识别率不再提高。
|
Download:
|
|
图 5 目标识别率随尺度数变化趋势 Fig. 5 Target recognition rate variation with scale number |
|
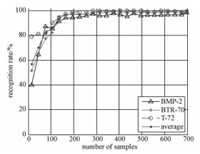
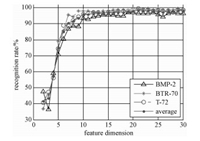
本节分别从字典原子数(即训练样本数)和字典原子维数(PCA降维特征维数)出发,研究稀疏字典规模对识别率的影响。图 6是平均识别率以及各类目标识别率随训练样本数变化的趋势图,图 7是平均识别率和各类目标识别率随特征维数变化的趋势图。图 6中,当训练样本数小于300时,平均识别率随其增多而提高;当训练样本数继续增加时,平均识别率不再明显提高。图 7中,当特征维数小于10时,平均识别率随着其增加而提高,特征维数在10到20区间,平均识别率随其增加而略有提高;当维数为21时,平均识别率达到最高,当维数大于21时,平均识别率随着维数的增加而略有起伏,没有提高的趋势,已没有上升的空间,保留更多的特征对识别率的影响很小。
|
Download:
|
|
图 6 目标识别率随训练样本数的变化趋势 Fig. 6 Target recognition rate variation with number of train samples |
|
|
Download:
|
|
图 7 目标识别率随特征维数变化趋势 Fig. 7 Target recognition rate variation with feature dimension |
|
综合图 6和图 7,在本实验中,在一定范围内识别率随着训练样本数和特征维数的增加而提高,超过一定范围识别率不再提高,由此可以确定一个字典规模范围使得识别率达到最高的同时字典规模最小(如本实验中为训练样本数为300,特征维数为21,平均识别率达到最高98.72%),可以最大限度地节省识别时间,提高识别效率。
4 结论本文利用Gabor滤波器对SAR目标图像提取多尺度特征,并引入稀疏表示模型,根据基于表示系数的判别准则完成了SAR目标识别。实验结果表明算法可有效克服空间域单一尺度特征分类的片面性和局限性,有着较好的抗空间域图像干扰的性能,在图像存在干扰的情况下比传统空间域单一尺度特征的稀疏目标识别方法有更高的识别率,因而具有更好的实用性。此外本文还研究了算法中不同参数配置对识别结果的影响,使得识别准确率和识别时间达到最优化平衡。
| [1] | Fennell M T, Wishner R P. Battlefield awareness via synergistic SAR and MTI exploitation[J]. IEEE Aerospace and Electronic Systems Magazine , 1998, 13 (2) :39–43. DOI:10.1109/62.656334 |
| [2] | 王保云, 张逸为, 张荣, 等. 一种基于动态字典学习的SAR图像目标识别算法[J]. 光电工程 , 2013, 40 (6) :17–25. |
| [3] | 陈玲艳, 刘智, 张红. 基于水体散射特性的SAR图像水体检测[J]. 遥感技术与应用 , 2014, 29 (6) :963–969. |
| [4] | 周雨, 王海鹏, 陈思喆. 基于数值散射模拟与模型匹配的SAR自动目标识别研究[J]. 雷达学报 , 2015, 4 (6) :666–673. |
| [5] | Novak L M. State-of-the-art of SAR automatic target recognition[C]//Record of the IEEE 2000 International Radar Conference. IEEE, 2000:836-843. |
| [6] | Novak L M, Owirka G J, Brower W S. Performance of 10-and-20-target MSE classifiers[J]. IEEE Transactions on Aerospace and Electronic Systems , 2000, 36 (4) :1279–1289. DOI:10.1109/7.892675 |
| [7] | Zhao Q, Principe J C. Support vector machines for SAR automatic target recognition[J]. IEEE Transactions on Aerospace Electronic Systems , 2001, 37 (2) :643–654. DOI:10.1109/7.937475 |
| [8] | Mallat S G, Zhang Z. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing , 1994, 41 (12) :3397–3415. |
| [9] | Chen S S, Donoho D L, Saunders M A. Atomic decomposition by basis pursuit[J]. Siam Review , 2001, 43 (1) :33–61. |
| [10] | Thiagarajan J J, Ramamurthy K N, Knee P, et al. Sparse representations for automatic target classification in SAR images[C]//International Symposium on Communications, Control and Signal Processing, 2010:1-4. |
| [11] | 刘中杰, 庄丽葵, 曹云峰, 等. 基于主元分析和稀疏表示的SAR图像目标识别[J]. 系统工程与电子技术 , 2013, 35 (2) :282–286. |
| [12] | 程建, 黎兰, 王海旭. 稀疏表示框架下的SAR目标识别[J]. 电子科技大学学报 , 2014, 43 (4) :524–529. |
| [13] | 齐会娇, 王英华, 丁军, 等. 基于多信息字典学习及稀疏表示的SAR目标识别[J]. 系统工程与电子技术 , 2015, 37 (6) :1280–1287. |
| [14] | Witkin A P. Scale-space filtering[C]//International Joint Conference on Artificial Intelligence. 1983:329-332. |
| [15] | Marčelja S. Mathematical description of the responses of simple cortical cells[J]. Journal of the Optical Society of America , 1980, 70 (11) :1297–1300. DOI:10.1364/JOSA.70.001297 |
| [16] | Daugman J G. Complete discrete 2-D Gabor transforms by neural networks for image analysis and compression[J]. IEEE Transactions on Acoustics Speech & Signal Processing , 1988, 36 (7) :1169–1179. |
| [17] | Tropp J, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory , 2008, 53 (12) :4655–4666. |
| [18] | Wipf D P, Rao B D. An empirical bayesian strategy for solving the simultaneous sparse approximation problem[J]. IEEE Transactions on Signal Processing , 2007, 55 (7) :3704–3716. DOI:10.1109/TSP.2007.894265 |
| [19] | Min H B, Rong P, Wu T, et al. Automated segmentation of mouse brain images using extended MRF[J]. Neuroimage , 2009, 46 (3) :717–725. DOI:10.1016/j.neuroimage.2009.02.012 |
| [20] | Larlus D, Jurie F. Combining appearance models and Markov random fields for category level object segmentation[C]//IEEE Conference on Computer Vision & Pattern Recognition, 2008:1-7. |
 2017, Vol. 34
2017, Vol. 34 


