液晶衍射光栅(liquid crystal optical phased array,LCOPA)是以液晶电控双折射效应为工作原理制作而成的强衍射光学器件。它能够对与液晶分子长轴方向一致的入射偏振光产生相位调制和类似闪耀光栅的不同级次衍射光。液晶衍射光栅在电场作用下可以实现光束控制,与传统的光控器件相比具有稳定性高、质量轻、体积小和速度快等优点。在光束控制与偏转、光通信以及波前校正等方面具有广泛的应用前景。针对液晶衍射光栅相位调制的测量是该器件研制过程中一个极为重要的环节和评价其性能的主要方法。
早在1991年,Raytheon公司研制成功43 000阵列的4.3 cm×4.1 cm一维液晶相位光栅,并介绍了液晶光学相控阵相关技术及其在激光雷达、空间光通信中的应用前景[1-2]。2002年,赵晓凤等[3]提出共光路的径向剪切干涉法实现对液晶空间光调制器(LCSLM)调制相位分布的测量,其原理为对液晶空间光调制器所产生的畸变波面进行径向的放大和缩小,使其空间叠加产生干涉。对干涉条纹进行傅里叶变换多次迭代得出调制相位分布。液晶空间光调制器的工作原理与液晶光栅类似,均利用液晶电控双折射效应,理论上该方法也可用于液晶光栅调制相位分布的检测,但多次傅里叶变换和迭代算法计算繁琐、速度慢。2011年,郑春艳等[4]提出一种基于共轭移相的干涉技术,并首次公布了液晶光栅的调制相位的分布形貌。但该结构为四分光镜的Mach-Zehnder结构,器件调整过程复杂、体积大、检测系统易受外界环境干扰。因此,目前针对液晶衍射光栅相位调制的测量与标定尚未有比较完善的解决途径,波前相位干涉系统的稳定性和算法复杂度难以取得有效统一[3-4]。
针对液晶衍射光栅波前相位检测干涉方法的不足,本文提出正交移相干涉测量液晶衍射光栅波前调制相位分布的方法。对于该检测系统,在PBS出射前,信号臂和参考臂不共光路,但是从PBS出射的正交偏振光完全共光路,该结构是Twyman-Green的改型,并使用Jones矩阵推导出简单快速的相位恢复算法。对于PZT相移器,一般只知道PZT的电压位移特性[5-6],不利于相移可控和相位恢复算法的应用。2004年罗印龙[6]采用PZT相移引起明暗干涉条纹变化的计数方法,标定PZT相移器的驱动电压与位移曲线。此方法对相邻两步驱动电压的时间间隔和信号计数精度要求较高。由于干涉条纹呈正弦强度分布,本文采用正弦拟合算法对一维光强进行拟合,得到不同相移电压对应的正弦参数(角频率、幅值、相位),直接标定出PZT相移器驱动电压与相移曲线。采用四参数正弦拟合算法[7]标定出PZT的电压相移曲线,使这套系统的相移可控。实验中对透射式相位板调制的透射波前进行检测,其结果与美国商用干涉仪WYKO的测试结果对比,验证测量方法的可行性和准确性,使用同样的方法完成对液晶衍射光栅调制相位分布的测量。
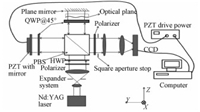
1 测量原理与相位恢复算法 1.1 测量原理如图 1所示,1 064 nm Nd:YAG激光器发出的连续光经过扩束镜扩束,到达起偏器形成线偏振光。线偏振光透过快轴沿坐标轴X方向的半波片(HWP)。接着经过偏振分光棱镜(PBS),透射的p光经快轴与X轴夹角为45°的1/4波片(QWP)后为左旋圆偏振光,透过待测物经反射镜反射回QWP后为s光,再次经PBS后反射出,该路光束为信号臂。另一路由PBS反射的s光同样经快轴与X轴夹角为45°的1/4波片, 受压电反射镜反射,再次穿过QWP后成为p光并透射过PBS,该路光束为参考臂。参考臂上的反射镜由PZT驱动产生亚微米级的移动,从而在两个臂上产生正交线偏振的相移。经PBS出射的p光和s光共轴输出,经过偏振方向与X轴成45°夹角的检偏器,通过放置在CCD共轭面的可调方形光阑后,两束偏振光在面阵探测器上重合相干。对于该检测系统,从PBS出射的信号光和参考光是共光路的,结合横向剪切干涉法共光路的特点,共光路结构对环境振动和空气扰动引起的测量误差将有所减少[3]。
|
Download:
|
|
图 1 正交移相干涉系统 Fig. 1 Orthogonal phase shift interferometry |
|
针对透射型液晶衍射光栅,根据液晶双折射效应,让液晶分子长轴方向与s光偏振方向平行,当液晶驱动器施加电压给液晶后,液晶分子长轴将沿电场方向转动从而在入射s光上引入附加相移。而对于入射到液晶器件的p光则不会引入附加相移。实现了正交偏振信号光与参考光的非等效的相位调制,使得液晶器件相位调制的检测可行。透射后的正交偏振光的相位特性为:PZT反射镜在p偏振方向上引入可控的相移,液晶器件在s偏振方向上引入一待测的附加相位,产生与传统的移相干涉仪等同的效果,但该结构却实现了信号臂与参考臂的准共光路。
1.2 相位恢复算法在偏振光干涉中,Jones矩阵计算方便,采用Jones矩阵推导所搭建系统的波前相位恢复算法。假设入射光束的琼斯矢量为
| $ \begin{array}{l} {\mathit{\boldsymbol{J}}_7}\left[ {\begin{array}{*{20}{c}} {{{\cos }^2}\theta }&{\frac{1}{2}\sin 2\theta }\\ {\frac{1}{2}\sin 2\theta }&{{{\sin }^2}\theta } \end{array}} \right];{\mathit{\boldsymbol{J}}_6} = \left[ {\begin{array}{*{20}{c}} 0&0\\ 0&1 \end{array}} \right]{{\rm{e}}^{{\rm{i}}\varphi }};\\ {\mathit{\boldsymbol{J}}_5} = \left[ {\begin{array}{*{20}{c}} 0&0\\ 0&1 \end{array}} \right];{\mathit{\boldsymbol{J}}_4} = \frac{1}{{\sqrt 2 }}\left[ {\begin{array}{*{20}{c}} 1&{ - i}\\ { - i}&1 \end{array}} \right];{\mathit{\boldsymbol{J}}_3} = \left[ {\begin{array}{*{20}{c}} { - 1}&0\\ 0&{ - 1} \end{array}} \right];\\ {\mathit{\boldsymbol{J}}_2} = \frac{1}{{\sqrt 2 }}\left[ {\begin{array}{*{20}{c}} 1&{ - i}\\ { - i}&1 \end{array}} \right];{\mathit{\boldsymbol{J}}_1} = \left[ {\begin{array}{*{20}{c}} 1&0\\ 0&0 \end{array}} \right]. \end{array} $ | (1) |
J7, J6…J1分别表示从检偏器到半波片s偏振光传输路径上所经过的光学系统的琼斯矩阵[8]。其中φ为待测物体调制相位,θ为检偏器偏振方向与坐标系X轴的夹角。经过计算得到
| $ {{\mathit{\boldsymbol{E'}}}_{\;1}} = \prod\limits_{i = 1}^7 {{\mathit{\boldsymbol{J}}_{8 - i}}{\mathit{\boldsymbol{E}}_1}} = \left[ \begin{array}{l} \frac{{{A_1}i}}{2}\sin 2\theta \\ {A_1}i\;{\sin ^2}\theta \end{array} \right]{{\rm{e}}^{{\rm{i}}\varphi }}. $ | (2) |
同样对于面阵CCD像空间p偏振光
| $ \begin{array}{l} {\mathit{\boldsymbol{J}}_7}\left[ {\begin{array}{*{20}{c}} {{{\cos }^2}\theta }&{\frac{1}{2}\sin 2\theta }\\ {\frac{1}{2}\sin 2\theta }&{{{\sin }^2}\theta } \end{array}} \right];{\mathit{\boldsymbol{J}}_6} = \left[ {\begin{array}{*{20}{c}} 0&0\\ 0&1 \end{array}} \right];\\ {\mathit{\boldsymbol{J}}_5} = \left[ {\begin{array}{*{20}{c}} 0&0\\ 0&1 \end{array}} \right];{\mathit{\boldsymbol{J}}_4} = \frac{1}{{\sqrt 2 }}\left[ {\begin{array}{*{20}{c}} 1&{ - i}\\ { - i}&1 \end{array}} \right];\\ {\mathit{\boldsymbol{J}}_3} = \left[ {\begin{array}{*{20}{c}} { - 1}&0\\ 0&{ - 1} \end{array}} \right]{{\rm{e}}^{{\rm{i}}\frac{{2{\rm{ \mathsf{ π} }}}}{\lambda }\left( {2\Delta } \right)}};{\mathit{\boldsymbol{J}}_2} = \frac{1}{{\sqrt 2 }}\left[ {\begin{array}{*{20}{c}} 1&{ - i}\\ { - i}&1 \end{array}} \right];\\ {\mathit{\boldsymbol{J}}_1} = \left[ {\begin{array}{*{20}{c}} 0&0\\ 0&1 \end{array}} \right]. \end{array} $ | (3) |
经过计算得到
| $ {{\mathit{\boldsymbol{E'}}}_{\;2}} = \left[ \begin{array}{l} {B_1}{\cos ^2}\theta \\ \frac{{{B_1}i}}{2}\sin 2\theta \end{array} \right]{{\rm{e}}^{{\rm{i}}\frac{{2{\rm{ \mathsf{ π} }}}}{\lambda }\left( {2\mathit{\Delta }} \right)}}. $ | (4) |
在面阵探测器上的合振幅分布为
| $ \mathit{\boldsymbol{E' = }}{{\mathit{\boldsymbol{E'}}}_{\;1}} + {{\mathit{\boldsymbol{E'}}}_{\;2}} = \frac{i}{2}\left[ \begin{array}{l} {A_1}\sin 2\theta {{\rm{e}}^{{\rm{i}}\varphi }} + 2{B_1}{\cos ^2}\theta {{\rm{e}}^{{\rm{i}}\frac{{2{\rm{ \mathsf{ π} }}}}{\lambda }\left( {2\mathit{\Delta }} \right)}}\\ 2{A_1}{\sin ^2}\theta {{\rm{e}}^{{\rm{i}}\varphi }} + {B_1}\sin 2\theta {{\rm{e}}^{{\rm{i}}\frac{{2{\rm{ \mathsf{ π} }}}}{\lambda }\left( {2\mathit{\Delta }} \right)}} \end{array} \right]. $ | (5) |
不失一般性,为简单起见,设检偏器偏振方向与X轴成45°,则由此计算得到其干涉光强分布为:
| $ I = {\left| {E'} \right|^2} = \frac{1}{4}\left( {A_1^2 + B_1^2} \right) + \frac{1}{2}{A_1}{B_1}\cos \left( {\varphi - \frac{{4{\rm{ \mathsf{ π} }}\mathit{\Delta }}}{\lambda }} \right). $ | (6) |
设驱动压电反射镜移动量Δ分别为0,λ/8,λ/4,3λ/8,则干涉光强分别为:
| $ \begin{array}{l} {I_1} = \frac{1}{4}\left( {A_1^2 + B_1^2} \right) + \frac{1}{2}{A_1}{B_1}\cos \varphi ,\\ {I_2} = \frac{1}{4}\left( {A_1^2 + B_1^2} \right) + \frac{1}{2}{A_1}{B_1}\sin \varphi ,\\ {I_3} = \frac{1}{4}\left( {A_1^2 + B_1^2} \right) - \frac{1}{2}{A_1}{B_1}\cos \varphi ,\\ {I_4} = \frac{1}{4}\left( {A_1^2 + B_1^2} \right) - \frac{1}{2}{A_1}{B_1}\sin \varphi . \end{array} $ | (7) |
则由4幅干涉图计算得到的包裹相位为
| $ \varphi = {\tan ^{ - 1}}\frac{{{I_4} - {I_2}}}{{{I_3} - {I_1}}}. $ | (8) |
要通过式(8)得到包裹相位,需要采集压电反射镜移动量Δ分别为0,λ/8,λ/4,3λ/8的干涉图样,要求必须能精确控制PZT移相器的每一步移相值,因此需标定出PZT相移器的电压相移曲线。对于未加入待测物的正交移相干涉系统,通过PZT驱动电源的电压控制压电陶瓷,以0.01 V为PZT驱动电压步进,14 V为上界,同步拍摄0~14 V范围内的1 400帧400×400的干涉图像。
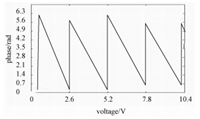
不同电压下的干涉图像的相位会随着压电陶瓷微位移的变化而变化,对每一帧干涉图像进行反高斯滤波和中值滤波。采用四参数正弦拟合算法[7]拟合出每帧干涉图像的相位。标定出压电陶瓷驱动电压和相位的特性曲线,如图 2所示。由于PZT具有迟滞性[5],所以曲线存在少量基线漂移,漂移量在0.5 rad。并且因为PZT本身的特性和闭环负反馈,其相移特性具有明显的周期性。一个周期PZT相移为0.5~6.3 rad,变化量接近2π,电压周期为2.6 V,电压相移基本成线性关系。
|
Download:
|
|
图 2 PZT电压相移曲线 Fig. 2 Voltage vs. phase curve of PZT |
|
为了检验搭建系统和恢复算法的有效性,先使用透射式相位板进行波前检测实验。在一路反射镜前加入通光孔径ϕ25.4 mm透射式相位板。采用陕西维视的MV-1300UM工业相机,最高分辨率为1 280 pix×1 024 pix,像元尺寸为5.2 μm×5.2 μm。拍摄640×480图像时,帧率可达45 fps,满足图像采集的实验条件。PZT压电陶瓷选用哈尔滨芯明天的VS 18系列高压叠堆封装陶瓷,配合XE 501型高压驱动器,具有闭环控制和上位机通信功能。光源采用1 064 nm YAG光纤准直平行光管。在正交移相干涉中,为了减小实验误差需要选择准确度适当的光学元件,对光路要精确调整[9-10]。搭建的实验装置如图 3所示。

|
Download:
|
|
图 3 相位板透射波前检测实验装置 Fig. 3 Experiment structure for wavefront measurement of phase board |
|
根据所推导的相位恢复算法,需要采集驱动压电反射镜移动量Δ分别为0,λ/8,λ/4,3λ/8的干涉图样。采用分段线性插值法对图 2的相移曲线插值,得到相位变化在0, π/4, π/2, 3π/4下的驱动电压。采集这4个电压值对应的4幅干涉条纹图,如图 4所示。干涉条纹图样有一定弯曲,但对于四参数正弦拟合的数据采样和相位恢复并不是误差来源[10]。通过推导的相位恢复算法,得到透射式相位板包裹相位,为减少离散相位信息丢失,使用Zernike多项式进行波前数据拟合[11-12],得到的解包裹后的三维波前如图 5(a)所示。

|
Download:
|
|
图 4 不同相移干涉条纹图 Fig. 4 Different phase shift interferograms |
|

|
Download:
|
|
图 5 正交移相干涉法测量的相位板透射波前与WYKO的对比 Fig. 5 Comparison of measured wavefront results of phase board between orthogonal phase shift interferometry and WYKO |
|
为了检验测量结果的准确性,采用对比实验法,将正交移相干涉系统的相位板测量结果与美国商用干涉仪WYKO的结果做对比分析。如图 5(a)和5(b)、5(c),二者测出的相位板的三维波前面形基本一致,三维波前图整体略有偏移,但不影响其相对值。表 1中数据是WYKO干涉仪的测量结果与正交移相系统Zernike多项式拟合结果。结果表明搭建的移相干涉系统与WYKO干涉仪测试结果相比,P-V值误差小于λ/75,RMS值误差小于λ/240,达到较高的精度。
|
|
表 1 正交移相干涉系统和WYKO干涉仪测量数据对比 Table 1 Comparison of measurement data between orthogonal phase shift system and WYKO |
验证了正交移相干涉相位分布测量方法的准确性,分析测量误差后,将图 1和图 3中的透射式相位板撤下。将自制的液晶光栅作为待测物放置在共轭光学系统物面上(光阑附近),使液晶面与CCD像面共轭,以捕捉更多级次的衍射光。因为PBS出射端的s偏振光偏振方向与液晶分子长轴方向一致,液晶光栅对面阵CCD像空间的s偏振光有相位调制,对p偏振光无相位调制。此时相位恢复算法中的φ为液晶光栅产生的相位调制,适用相位恢复算法。采用同样的相位测量计算方法得到5 V驱动电压下液晶衍射的相位调制分布,如图 6所示。图 6(b)为液晶光栅远场±2级衍射光斑实测,图 6(c)中液晶光栅的相位分布在0~2π之间,远场光斑与相位分布相对应。

|
Download:
|
|
图 6 正交移相干涉法测量的液晶光栅透射波前相位 Fig. 6 Phase distribution of LCOPA by orthogonal phase shift interferometry |
|
本文提出正交移相干涉测量液晶衍射光栅调制相位分布的方法。搭建正交移相干涉系统测量相位板透射波前,通过与WYKO商用干涉仪测量结果的对比实验,验证了正交移相干涉波前测量方法的准确性和可行性。其中标定出PZT相移器的电压相移特性曲线,实现了相移可控,使相位恢复算法具有可行性。使用该方法测量出自制液晶衍射光栅的调制相位分布和远场光斑分布,对今后液晶衍射光栅的研制和性能测试有一定的指导意义。
感谢汪相如副研究员在液晶衍射光栅方面的帮助。| [1] | Mcmanamon P F, Dorschner T A, Corkum D L, et al. Optical phased array technology[J]. Proc IEEE , 1996, 84 (2) :268–298. DOI:10.1109/5.482231 |
| [2] | Dorschner T A, Friedman L J, Holz M, et al. An optical phased array for lasers[J]. Proc IEEE , 1996, 96 (6) :1–7. |
| [3] | 赵晓凤, 李大海, 陈祯培. 利用径向剪切干涉法测量液晶空间光调制器的位相调制特征[J]. 四川大学学报:自然科学版 , 2002, 39 (4) :657–661. |
| [4] | 郑春艳, 杨若夫, 徐林, 等. 液晶闪耀光栅波前相位测量方法研究[J]. 中国激光 , 2011, 38 (10) :181–186. |
| [5] | 朱波.移相式斐索中波红外干涉仪关键技术及应用研究.南京:南京理工大学, 2014. http://cn.bing.com/academic/profile?id=b3bc98134144f98a0bb9c2004906079f&encoded=0&v=paper_preview&mkt=zh-cn |
| [6] | 罗印龙.PZT相移系统及其标定方法的研究与应用.昆明:昆明理工大学, 2004. http://cn.bing.com/academic/profile?id=3e186468c2281b0066ff59b26de47761&encoded=0&v=paper_preview&mkt=zh-cn |
| [7] | 梁志国, 张大治, 孙璟宇, 等. 四参数正弦波曲线拟合的快速算法[J]. 计测技术 , 2006, 6 (1) :4–7. |
| [8] | 郁道银, 谈恒英. 工程光学[M]. 北京: 机械工业出版社, 2006 . |
| [9] | 钱林勇, 黄元申, 张大伟, 等. 基于激光干涉仪的衍射光栅波前检测[J]. 光电工程 , 2013, 40 (3) :67–74. |
| [10] | 杨军, 刘志海, 范立波. 波片对激光干涉仪非线性误差的影响[J]. 光子学报 , 2008, 37 (2) :364–369. |
| [11] | 张强, 姜文汉, 许冰. 利用Zernike多项式对湍流波前进行波前重构[J]. 光电工程 , 1998, 25 (6) :15–19. |
| [12] | 惠梅, 牛憨笨. 运用泽尼克多项式进行物面波前数据拟合[J]. 光子学报 , 1999, 28 (12) :1113–1116. |
 2017, Vol. 34
2017, Vol. 34 


