鳐鱼是一种底栖动物,胸鳍宽大,鱼体呈圆或菱形(俯视),在游动时靠胸鳍作波状摆动而前进。通常,鳐鱼游动过程中身体与底面(或物面)维持较小的距离,这不仅有利于捕食水底的生物,也有利于利用近壁面效应来游动[1]。
鳐鱼没有鳔,无法通过改变身体密度实现上浮和下潜。在近壁面游动中,为维持与底面的距离,必须通过游动方式保持游动中的身体平衡,使其所需的升力和力矩几乎为零。因此,对于鳐鱼在近壁面游动时产生的壁面效应,不需关注壁面效应如何提高升力,而应关注如何调节升力为零;另一方面,需要更多地关注鳐鱼这种游动方式的推力和推进效率。
为研究鳐鱼这种近壁游动的流体力学问题,研究者们通常把鳐鱼的胸鳍看作柔性翼,从而把该问题简化成在近壁附近波动翼的水动力学问题,而这方面的研究工作刚刚起步,并以实验测量为主。Blevins和Lauder[2]研究低波数柔性薄板在靠近壁面时的水动力学特性,发现壁面的存在并不会使游动更快,反而使功率消耗增大,这意味着近壁面的游动是负面的。然而,Quinn等[3]通过实验发现柔性薄板在壁面附近时推力更大,可使游速增加,推进效率更高,该结果与Fernández-Prats等[4]的薄翼实验结果一致。上述实验工作有一个共性,都是通过柔性板或翼的被动变形模拟鱼体变形,变形程度和波数依赖于材料性质与板的长度。一方面,在Blevins和Lauder的实验中波数(体长/波长)为0.5,而Quinn等和Rafael等的实验中波数接近1.0,而近壁面游动时鳐鱼的波数在0.8到1.0之间。另一方面,鳐鱼胸鳍或者鱼体波动是一种主动变形,与被动变形不同。前人对鱼类游动的研究发现,鱼类通过主动控制,使波动翼的波速大于来流速度(游动速度)时,翼才会获得推力[5]。因此,研究鳐鱼或鱼体的近壁面游动时,须建立合理的物理模型,这样才能利用波动翼在近壁面的水动力学特性揭示鳐鱼的推进机制。
本文利用基于速度势的非定常面元法研究给定波动规律的二维薄翼的壁面效应。首先研究鳐鱼近壁面的推进机理,然后探讨升力的调节规律(使得升力均值为零);其次,讨论波动翼的推力和推进效率,进而探讨鳐鱼的近壁面游动特征。作为初步研究,本文不探讨波动翼的力矩问题,这将是下一步的研究工作。
1 计算模型与方法鳐鱼的游动一般都处于高雷诺数范围(Re≈105),此时的流场中绝大部分可以近似为无黏的,黏性主要体现在鱼体表面的边界层和鱼体尾部脱出的剪切层。故可以把这类游动简化为无黏势流和鱼体尾缘脱出的涡层,且在尾缘处满足Kutta条件。经上述简化,就可以采用非定常面元法研究鳐鱼的游动,该方法不仅可以模化旋涡的生成和演化,还便于从涡动力学的角度分析物体的受力,从而更好地理解流动物理。
1.1 物理模型鳐鱼的身体与胸鳍构成一个整体,主要靠宽大的胸鳍波动产生动力。根据前人[1, 6-7]的实验观测,胸鳍的运动可被看作由前向后传播的波,且波幅由身体内侧向外侧增大。这类三维的波动较为复杂,不便于理解鳐鱼的推进机理。因此,仿照前人的模型实验[2-4],本文先建立一个简化的二维模型,抓住主要特征(波动)研究近壁面效应,为将来研究三维波动提供参考。
如图 1所示,以典型的圆鳐为例,在距离鳐鱼身体中线约2/3展长位置处做胸鳍的纵剖面,该纵剖面形状接近于一个厚度为5%的翼型[8],故可简化为NACA0005翼型(厚度为5%弦长的对称翼型)。因此,鳐鱼胸鳍的波动可以简化为NACA0005翼型的波动运动。

|
Download:
|
|
图 1 鳐鱼胸鳍的简化模型 Fig. 1 Simplified model of the pectoral fin of a batoid fish |
|
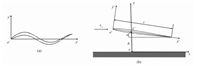
根据观测[7],鳐鱼纵剖面各点的波动幅度近乎相等,故而可以把剖面的运动简化成NACA0005翼型的等波幅的右行波(头部朝左),如图 2(a)所示。在随体坐标系o′x′y′中,翼型中线的波动可由下式描述
| $ y' = a\sin \left[ {2{\rm{\pi }}\left( {kx' - ft} \right)} \right] $ | (1) |
|
Download:
|
|
图 2 翼型壁面效应的物理模型(C为质心) Fig. 2 Physical model of a foil near a flat ground |
|
其中:a为波动的幅值,k为波数,f为频率。在此假定翼型波动时身体厚度不变,且在x′轴的投影长度不变。则翼型表面的变形速度可近似为在中线上对应点的振动速度。
作为初步研究,鳐鱼的近壁面游动可以看作是二维鳐鱼模型在平壁面附近的波动运动。如图 2(b)所示,在壁面参考系oxy中,二维鳐鱼模型的体长为c,质心到平壁面的高度为h,鱼体的仰角(与平壁面的夹角)为α。设来流速度为v∞,水的密度为ρ。
在本文的流体力学问题中选择体长c、速度v∞和密度ρ为特征长度、速度和密度,用以对其他物理量进行无量纲化。为简化描述,在下文的陈述中,波幅a,波数k,频率f以及距离壁面的高度h等所有物理量均指无量纲量。
1.2 计算方法面元法是一种快速估算运动物体受力的数值方法,基本思想是通过在流场区域的边界上分布某些特定的基本流动解(如点源,点涡,偶极子等)模拟整个流场区域内的流动[9-11]。早在1999年,Wolfgang[12]已经成功地将该方法应用于鱼类游动的数值模拟,并取得了可信的结果。
针对带水平壁面的情况,本文采用镜像法[13]处理水平壁面问题,即通过相对水平壁面对称分布的面元和尾涡(点源、点涡、偶极子等)来等价壁面存在的情形,使得平壁面始终为一条流线。
当求得流场中点源、偶极子等的分布后,流场便由Biot-Savart公式唯一确定。最后物体的表面压强可以由非定常的伯努利方程来求解,即
| $ \frac{{\partial \varphi }}{{\partial t}} + \frac{{{v^2}}}{2} + \frac{p}{\rho } = \frac{{v_\infty ^2}}{2} + \frac{{{p_\infty }}}{\rho }, $ | (2) |
其中:v和p分别表示流场中任一点处的速度和压强,v∞和p∞分别表示无穷远处的速度和压强。故,可以求得物面的无量纲压强分布
| $ {C_p} = \frac{{p - {p_\infty }}}{{0.5\rho v_\infty ^2}} = 1 - \frac{{{v^2}}}{{v_\infty ^2}} - \frac{2}{{v_\infty ^2}}\frac{{\partial \varphi }}{{\partial t}}, $ | (3) |
进而求得翼型的推力和升力系数:
| $ {C_{\rm{T}}} = \oint_{{S_B}} {{C_p}{n_x}{\rm{d}}l,} $ | (4) |
| $ {C_{\rm{L}}} = - \oint_{{S_B}} {{C_P}{n_y}{\rm{d}}l.} $ | (5) |
其中:CT和CL的正方向分别定义为x轴的负向和y轴正向;SB为翼型表面;(nx, ny)为物面单位外法向量。那么,一个周期内的平均升力和平均推力可分别记为CL和CT,翼型的推进效率采用Froude效率
| $ \eta = \frac{{{{\bar C}_{\rm{T}}}{v_\infty }}}{{{C_{{\rm{pw}}}}}}, $ | (6) |
其中功率耗费由
为表征平壁面的存在对波动翼推力和推进效率的影响大小,在本文中定义平均推力增量和推进效率增量如下:
| $ \Delta {{\bar C}_{\rm{T}}} = {{\bar C}_{\rm{T}}}\left( h \right) - {{\bar C}_{\rm{T}}}\left( { + \;\;\infty } \right), $ | (7) |
| $ \Delta \eta = \eta \left( h \right) - \eta \left( { + \;\;\infty } \right). $ | (8) |
若平均推力和推进效率的增量越大,则表明壁面效应越强(h=+∞表示无壁面的情况)。
需要注意的是,由于面元法采用无黏势流模型,当翼型极其靠近壁面时,黏性的影响加大导致其预测结果不再准确。尤其对升力而言,面元法的结果要比黏性模型偏低。Moryossef和Levy[14]对固定翼和振荡翼型的模拟结果表明:在翼型高度大于0.5时,黏性影响可完全忽略;当翼型高度低于0.15到0.5之间时,无黏流动效应占主导地位;当翼型高度小于0.15后,黏性效应显现。因此,在本文的研究中,为保证预测结果的正确性,对波动翼到平壁面的高度做了限定,即
| $ h - a > 0.15. $ | (9) |
为验证面元法程序的正确性,本文先对网格密度和时间步长进行验证,然后用已有的波动翼型的实验和CFD模拟结果进行验证。
2.1 程序验证选取NACA0005翼型在无穷域的均匀来流中作零仰角(α=0)波动运动,波数k=0.8,波动频率f=2.0,波幅a=0.1。翼型上划分n个网格,采用余弦划分方法;在一个周期内使用m个时间步。结果如图 3和图 4所示。

|
Download:
|
|
图 3 网格验证 Fig. 3 Grid verification |
|

|
Download:
|
|
图 4 时间步长验证 Fig. 4 Time step verification |
|
图 3和图 4分别给出不同网格数n和不同时间步数m计算条件下,一个振荡周期内升力和推力系数随时间的变化规律。结果表明,当网格数为200时,计算结果不依赖于网格的选取;当时间步数大于200时,计算结果收敛。故在此后的计算中,网格数为200,时间步长为0.005(m=200)。
2.2 程序确认2008年,胡文蓉[8]使用厚度为5%的波动翼型模拟Clark和Smits[15]对“前口蝠鲼”模型实验。本文选取相同的模型(k=0.4,f=1.33,a=0.23),计算波动翼型一个周期内的平均推力,并与他们的结果进行对比。如表 1所示,本文的结果与胡文蓉的数值模拟以及Clark和Smits的模型实验结果相符。由此可见,本文采用的面元法可以用来预估波动翼的受力,结果是可靠的。
|
|
表 1 波动翼型平均推力 Table 1 Average thrust coefficients of an undulating foil |
鳐鱼在壁面附近的平稳游动,须保持与平壁面的距离不发生改变,这就需要稳定的推力来克服游动的阻力,以及平衡的升力(预设为零)。因此,本节首先研究推力的产生机理,随后探讨升力平衡的调节机制。
3.1 推力产生的机理及近壁效应根据实验观测[7],鳐鱼的无量纲波数k约为0.8,无量纲的波幅a约为0.04~0.12,无量纲频率f约为1.2~2.4。当游速为每秒1倍体长时,无量纲的波幅和频率分别为0.08和1.6,此时,无量纲的波速为f/k≈2.0,大于来流速度。当鳐鱼贴近壁面游动时,身体仰角较小,不妨先预设仰角α为0°。
为研究不同高度对推力的影响,在此选择波数0.8、波幅和频率分别为0.08和1.6,以及3个典型的高度值(h=+∞、1.00和0.30)确定计算参数,并通过面元法计算推力随时间变化的规律。
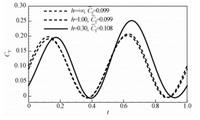
图 5为一个周期内推力的时变曲线。从图中可以看出:1)在一个周期内推力出现了2个峰值;2)当距离壁面的高度大于1时,推力曲线变化很小;3)当高度小于1时,第2个推力峰值增加,这也导致平均推力的增加。
|
Download:
|
|
图 5 波动翼型推力的近壁变化 Fig. 5 Thrust-time curves of an undulating foil near a ground |
|
为揭示推力产生的机理,图 6显示了波动翼的尾涡图像,其中实线为距离壁面高度为h=0.3的涡层分布,虚线为无壁面(h=+∞)的情形(为了对比,把波动翼在y方向平移到h高度)。从尾涡的总体结构来看,二者相差并不大,皆呈“反卡门涡街”排布,上排涡列为正涡,下排涡列为负涡。但是,在细微处,二者的涡层并不完全重合。从涡动力学的观点来看,不仅需要分析涡的结构,还必须定量分析涡的强度大小,这样才能获得足够的信息。

|
Download:
|
|
图 6 波动翼型尾涡结构 Fig. 6 Wake structure of an undulating foil |
|
因此在计算时,跟踪了在一个周期中尾涡的生成及演化,即记录了一个正涡团Γu和一个负涡团Γd的生成过程及其位置的变化。在图 6的尾涡结构图中,Γu和Γd已经远离了波动翼型。
在此,对于尾缘脱出来的Γu和Γd,其强度可以通过空间积分得到,其位置由涡心的位置来表示,以Γu为例:
| $ {\Gamma _u} = \int {{\gamma _u}{\rm{d}}} l, $ | (10) |
| $ {y_u} = \frac{{\int {y{\gamma _u}{\rm{d}}l} }}{{{\Gamma _u}}}, $ | (11) |
其中,γu表示涡层的强度。
图 7(a)表示选定的周期中Γu和Γd的大小随时间的变化规律。首先生成的是上排的涡团Γu,然后生成下排的涡团Γd;一个周期后,两涡团的强度维持不变。从图中还可以看到,无论是Γu还是Γd,靠近壁面的算例获得的绝对值都比无壁面情形大。

|
Download:
|
|
图 7 尾涡涡量、涡心和推力随时间的变化 Fig. 7 Changes in vorticity, center of the wake vortex, and their thrust with time |
|
图 7(b)给出Γu和Γd的涡心在y方向的位置随时间的变化规律。在生产涡团的过程中,涡团的中心位置变化较小,在周期的末期(深色阴影区),涡团的位置才有了差异。特别是下排涡团,它比上排涡团更靠近壁面,使得差异更明显。这种位置上的差异与涡强度的差异都由壁面的存在导致。
根据涡动力理论[16],这些涡的生成和演化与流体动量的变化有关,可以由涡动力学公式给出作用在物体上的流体力与流场中旋涡之间的关系(二维情形)
| $ \mathit{\boldsymbol{F = }} - \rho \frac{{\rm{d}}}{{{\rm{d}}t}}\int\limits_{V + {V_B}} {\mathit{\boldsymbol{r}} \times \mathit{\boldsymbol{\omega }}{\rm{d}}s + \rho \frac{{\rm{d}}}{{{\rm{d}}t}}\int\limits_{{V_B}} {\mathit{\boldsymbol{V}}{\rm{ds}}} ,} $ | (12) |
其中:ω为流场中的涡量,r为涡的位置,V为物体上各点的运动速度;VB为固体所占据的区域,V为流场区域。为探讨推力的机理,在本问题中可以计算出Γu和Γd对推力的贡献,以Γu为例:
| $ {\left( {{C_{\rm{T}}}} \right)_{{\Gamma _u}}} = \frac{{\rm{d}}}{{{\rm{d}}t}}\int {y{\gamma _u}{\rm{d}}l.} $ | (13) |
值得说明的是,当有壁面存在时,在式(13)的计算中需加入关于壁面对称的镜像作用。由于对称性,镜像涡的y和γu皆反号,所得的推力是式(13)计算的2倍,又由于波动翼和“镜像波动翼”的推力相等,所以Γu对波动翼推力的贡献仍由式(13)给出。
图 7(c)给出由式(13)计算出的Γu和Γd分别对波动翼推力的贡献。图中表明,在Γu产生的过程中,出现了1个推力峰,在Γd产生的过程中,出现了第2个推力峰。如果不考虑涡的分布,把涡都集中在涡心来看,则公式(13)可以得到简化,其中重要的一项
此外,由于壁面的存在,使得Γu和Γd的强度比无壁面情形大,所以对应的升力峰值变大。且Γd的涡心位置来看,它比Γu偏离翼型质心更多,这是导致第2个峰值增长明显的原因。
当经历一个周期后,Γu和Γd的强度不再变化,二者的y向间距也几乎不变,由公式(13)可知,此对旋涡对推力的贡献减小直至为零。但是,由于壁面的存在,不仅增长了涡的强度,也增大了两涡的y向间距,因此一个周期内的平均推力比无壁面的情形大,且推力主要由尾缘近场脱涡产生。
综上所述,波动翼型在一个周期内由于交替脱落的正向和反向涡,导致推力出现了2个峰值,且推力主要由尾缘近场脱涡引起的;当波动翼靠近壁面时,壁面的存在使得脱涡的强度增大,且略微增大了间距,这使得一个周期中的平均推力的增加。
3.2 升力的调节机制为保持鳐鱼质心距离平壁面的高度不变,需要调节波动翼的升力大小,使其趋于零。那么,鳐鱼在同样的波幅和波动频率下,是如何调节身体的升力呢?
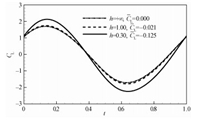
对比一下波动翼远离壁面和靠近壁面时的升力变化规律,如图 8所示(计算参数与3.1节相同)。结果表明,当波动翼靠近壁面时(h=0.3),升力在一个周期内的波动增大,平均值变为负(CL=-0.125)。这意味着,仰角为0°的波动翼在靠近壁面时,产生了向壁面的吸力。
|
Download:
|
|
图 8 仰角对近壁波动翼型平均升力的影响 Fig. 8 Influence of the attack angle on the average lift of an undulating foil near a ground |
|
调节升力的便捷方式就是提高仰角。因此,在不同高度(h为0.3~1.0)时,通过调节仰角(α为0°~4°)的大小,使得一个周期内的平均升力为零,从而获得零升力时的α(h)曲线,即如图 9所示的零升力曲线。

|
Download:
|
|
图 9 不同高度和仰角下的零升力曲线 Fig. 9 Zero-lift curves at different attack angle values and heights |
|
从图 9可以看出,随着波动翼距离壁面的高度降低,需要增大仰角以维持升力平衡;整体上,增大波幅或频率,可以降低零升力的α(h)曲线,这意味着在同一高度时,增大波幅和频率,可以减小仰角调整的调节量。
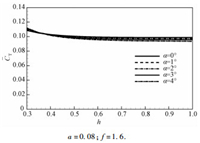
在实际的调节中,由于各参数的调节范围受到生理(变形幅度和输出功率等因素)或游动方式(速度控制)的限制,通常需要综合考虑参数的调节。譬如,波幅和频率的提高可能提高推力,使得鱼体向前加速,不能维持原有的速度游动。在此,图 10给出仰角调整后对平均推力的影响,结果表明,仰角对推力的影响较小。
|
Download:
|
|
图 10 仰角对近壁波动翼型平均推力的影响 Fig. 10 Influence of the attack angle on the average thrust of an undulating foil near a ground |
|
因此,在升力的调节机制中,调节仰角是最佳的选择。对于不同的波幅和频率组合,仰角随高度的变化规律是相似的,即随着距离壁面高度的减小,需要适当增大仰角。
4 波动翼推力与推进效率的壁面效应讨论在上一节里已经探讨了波动翼的推力产生机理和升力的调节机制,但对壁面效应的讨论并不多,本节将着重讨论壁面的存在对推力与推进效率的影响。
根据已有的计算结果,当波动翼距离平壁面的高度超过1倍体长时,其推力受到壁面的影响很小。因此,在设计算例的时候,高度h的变化范围控制在0.3到1.0之间。此外,其他的控制参数选取为:波数k=0.8,波幅a=0.08,频率f=1.6。由于仰角对推力的影响较小,不妨设为α=0°。
在本节的讨论中,首先探讨波动翼在波幅和频率改变后的壁面效应,再讨论二者对壁面效应的影响,最后对本文中的不足做个说明。
4.1 波幅对壁面效应的影响为探讨波动翼波动幅度对壁面效应的影响,在此选择不同波幅(a为0.04~0.12)的算例探讨平均推力和推进效率随高度的变化规律,结果如图 11所示。

|
Download:
|
|
图 11 波幅对近壁波动翼型平均推力和推进效率的影响 Fig. 11 Influence of the amplitude on the average thrust and propulsive efficiency of an undulating airfoil near a ground |
|
从图 11(a)可以看出,在近壁面处(小h值),推力曲线的斜率变化快,这意味着越接近壁面,推力得到增强。随着波幅的增大,不仅平均推力随高度变化的曲线整体提高,这种在近壁面附近推力增强的趋势得到了加强。因此,在所给的幅度范围内,波动翼的波幅越大,推力的壁面效应越大。
图 11(b)显示推进效率的规律。整体上,当波幅提高,Froude推进效率降低。但是,对给定的波幅,推进效率几乎不随高度发生变化(最大变化也仅为0.1%左右),即推进效率不受壁面效应的影响。
总之,波幅的增大将提高推力的壁面效应。
4.2 频率对壁面效应的影响当其他参数不变,仅改变波动翼的频率时,可以探讨频率对平均推力及推进效率壁面效应的影响。此时,f从1.2到2.0变化,计算结果如图 12。

|
Download:
|
|
图 12 频率对近壁波动翼型平均推力和推进效率的影响 Fig. 12 Influence of the wave number on the average thrust and propulsive efficiency of an undulating foil near a ground |
|
对比图 12和图 11可以发现,推力曲线和推进效率曲线的变化规律几乎一致,这表明频率对推力和推进效率的影响与波幅类似,即频率越大,推力越大,推力的壁面效应也越大,而推进效率几乎不受壁面影响。
4.3 关于壁面效应的讨论为进一步讨论波动翼的壁面效应与波动参数(波幅和频率)的关系,在此选择给定翼型到平壁面的高度(h=0.30),研究不同波幅和频率下的波动翼推力增量ΔCT和推进效率增量Δη变化规律。计算结果如图 13所示,横坐标为波幅,纵坐标为频率,图(a)中的曲线为推力增量的等值线,图(b)中的曲线为推进效率增量的等值线。

|
Download:
|
|
图 13 波幅和频率对平均推力增量ΔCT和推进效率增量Δη的影响云图 Fig. 13 Influences of amplitude and frequency on the increments of average thrust and propulsive efficiency of an undulating foil near a ground |
|
从图 13(a)可看出,无论是增大波幅还是频率,推力增量都会增大。根据推力增量的定义,它是同波幅和频率条件下,由于壁面存在导致的推力增加量。由此可见,增大波幅和频率提高壁面效应的大小。但从图 13(b)可以看到,在误差范围内,可以认为推进效率的增量几乎为零。
从涡动力角度来看,由于反卡门涡街导致的动量增量ΔP与两排涡列的宽度bks和涡强度Γ成正比,与涡列中两涡距离aks成反比,即
| $ \Delta P \propto \frac{{\Gamma {b_{ks}}}}{{{a_{ks}}}}. $ | (14) |
而波幅的增大使得宽度bks(≈2a)增大,频率的增大使得aks(≈v∞/f)减小,因此波幅和频率的增加都将增大动量的增量,从而导致推力增大。另一方面,波幅或频率增加相当于增大波动翼上每个点的振动速率,使得在一个周期内交替脱出的正涡和负涡的强度得到加强,从而也提高推力。整体上,从公式(14)可近似为ΔP∝Γaf,这说明当达到同样的推力增量时,振幅和频率之间近似地呈反比关系,这与图 13(a)的等值线相符。
上述分析表明,当鳐鱼加速前进时,不仅可以同时提高波幅和频率来增大推力,还可以适当降低身体与平壁面之间的距离,从而利用壁面效应进一步增大推力,提高游速。
4.4 不足之处作为对鳐鱼底栖游动的初步研究,本文的工作存在诸多的不足之处。首先,讨论推进效率时采用了Froude效率。从计算结果来看,波幅和频率越小(意味着游速越低),该效率越高。而实际鱼类的游动情形是,低速和高速游动都是低效率的。在Liu等[17]的工作中,计入生物体的标准代谢能耗,重新定义了效能比,这样才能解答这个问题。
其次,在研究推力产生的机理时仍存在2个问题:一是壁面存在导致了推力相位的延迟;二是上述分析中,Γu和Γd产生推力峰仅为总推力峰值的1/4。若要解答这2个问题,需要从涡动力学角度考虑附着涡(根据Kelvin定理,有Γu产生,就将对应地附着涡)对推力的贡献。这将在今后的进一步研究中得以阐明。
5 结论本文用二维波动翼型来模拟鳐鱼的近壁游动,分析在壁面附近波动翼产生推力的机理和调节升力的机制,从而为理解鳐鱼贴底游动的壁面效应提供依据。得到如下结论:
1)波动翼型产生的推力主要由尾缘近场脱涡引起,在一个波动周期内的2个峰值是由交替脱落的正向和反向涡导致的;平壁面的存在使得推力增强,这是由于近壁面时,尾缘的脱涡强度增大,且正反涡对的间距略微增大所致。
2)在升力的调节机制中,调节仰角是最佳的选择;对于不同的波幅和频率组合,仰角随高度的变化规律是相似的,即随着距离壁面高度的减小,需要适当增大仰角才能使得升力为零。
3)无论是增大波动翼的波幅还是频率,推力都将得到增大,且相应的壁面效应也增大。
从以上结论可知,当鳐鱼贴底游动时,由于靠近壁面,推力得到增强,从而可以提高游速。同时,需要适当提高身体的仰角来控制升力,从而维持与壁面的距离不变。
| [1] | Blevins E L, Lauder G V. Rajiform locomotion:three-dimensional kinematics of the pectoral fin surface during swimming in the freshwater stingray Potamotrygon orbignyi[J]. The Journal of Experimental Biology , 2012, 215 (18) :3231–3241. DOI:10.1242/jeb.068981 |
| [2] | Blevins E, Lauder G V. Swimming near the substrate:a simple robotic model of stingray locomotion[J]. Bioinspiration & Biomimetics , 2013, 8 (1) :016005. |
| [3] | Quinn D B, Lauder G V, Smits A J. Flexible propulsors in ground effect[J]. Bioinspiration & Biomimetics , 2014, 9 (3) :036008. |
| [4] | Fern & #225;ndez-Prats R, Raspa V, Thiria B, et al. Large-amplitude undulatory swimming near a wall[J]. Bioinspiration & Biomimetics , 2015, 10 (1) :016003. |
| [5] | Lighthill M J. Note on the swimming of slender fish[J]. Journal of Fluid Mechanics , 1960, 9 (2) :305–317. DOI:10.1017/S0022112060001110 |
| [6] | Rosenberger L J, Westneat M W. Functional morphology of undulatory pectoral fin locomotion in the stingray Taeniura lymma (Chondrichthyes:Dasyatidae)[J]. Journal of Experimental Biology , 1999, 202 (24) :3523–3539. |
| [7] | Rosenberger L J. Pectoral fin locomotion in batoid fishes:undulation versus oscillation[J]. Journal of Experimental Biology , 2001, 204 (2) :379–394. |
| [8] | 胡文蓉. 鳐的典型运动方式的水动力学数值研究[J]. 水动力学研究与进展:A辑 , 2008, 23 (3) :269–274. |
| [9] | Hess J L, Smith A M. Calculation of non-lifting potential flow about arbitrary three dimensional bodies. Douglas Aircraft Co Long Beach CA, 1962. |
| [10] | Hess J L. Calculation of potential flow about arbitrary three-dimensional lifting bodies. Douglas Aircraft Co Long Beach CA, 1972. |
| [11] | Katz J, Weihs D. Wake rollup and the Kutta condition for airfoils oscillating at high frequency[J]. AIAA Journal , 1981, 19 (12) :1604–1606. DOI:10.2514/3.60097 |
| [12] | Wolfgang M J. Hydrodynamics of flexible-body swimming motions. Boston:Massachusetts Institute of Technology, 1999. |
| [13] | Katz J, Plotkin A. Low-speed aerodynamics[M]. Cambridge: Cambridge University Press, 2001 . |
| [14] | Moryossef Y, Levy Y. Effect of oscillations on airfoils in close proximity to the ground[J]. AIAA Journal , 2004, 42 (9) :1755–1764. DOI:10.2514/1.6380 |
| [15] | Clark R P, Smits A J. Thrust production and wake structure of a batoid-inspired oscillating fin[J]. Journal of Fluid Mechanics , 2006, 562 :415–429. DOI:10.1017/S0022112006001297 |
| [16] | 童秉纲, 尹协远, 朱克勤. 涡运动理论[M]. 合肥: 中国科学技术大学出版社, 2009 . |
| [17] | Liu G, Yu Y L, Tong B G. Optimal energy-utilization ratio for long-distance cruising of a model fish[J]. Physical Review E , 2012, 86 (1) :016308. DOI:10.1103/PhysRevE.86.016308 |
 2017, Vol. 34
2017, Vol. 34 


