镧系元素光谱的研究不仅对原子物理学、天体物理学、等离子体物理学等学科的发展具有重大意义,而且在一些技术领域,如生物医学分析、细胞成像、节能冷光灯等也有着广泛的应用[1]。Sm原子是一种典型的镧系原子,其基组态为[Xe]4f66s2,价壳层有6个f电子,使得Sm原子的能级结构非常复杂,图 1依据美国国家标准与技术研究院(NIST)评估的Sm原子能级数据[2],给出基组态[Xe]4f66s2,奇宇称激发组态[Xe]4f66s6p、4f55d6s2、4f55d26s、4f65d6p以及偶宇称激发组态[Xe]4f65d6s、4f66s7s的能级范围分布。图中标记“?”的,表示能级的谱项标识尚未确定。

|
Download:
|
|
图 1 Sm原子能级分布 Fig. 1 Scheme of energy levels for Sm I |
|
近年来,随着多步激光激发以及探测技术的发展,对于Sm这样的复杂原子体系的光谱测量也取得了重大进展[3-13]。例如:Zhao等[11]利用双色三步激发和光电离探测技术,系统研究Sm原子30 040~38 065 cm-1范围内的偶宇称能级,不仅确定了198条激发态能级位置,还确定了它们的总角动量J值;杨騄等[13]利用三色多步激发和光电离探测技术,系统研究Sm原子44 443.5~45 511.8 cm-1范围内的奇宇称能级,获得194条激发态的能级位置,并确定了其中110条能级的总角动量J值。但目前对于这些能级、光谱数据的标识、分析的工作还很缺乏。
由于复杂的电子关联效应[14],Sm原子能级的理论研究进展较慢。Porsev[15]利用相对论组态相互作用方法,计算基组态4f66s2 7FJ(J=0~6), 奇宇称激发组态4f66s6p 9GJ(J=0~4)、9FJ(J=1, 2)以及偶宇称激发组态4f65d6s 9HJ(J=1~5)、9DJ(J=2, 3)共21条谱线的能级。其中,基组态的能级相对误差小于9%,但激发组态的能级相对误差大于14%,绝对误差大于1 600 cm-1。最近,Zhou等[14]不仅考虑价电子间的关联,还加入原子实(core)电子-价电子,甚至原子实电子间的关联效应来提高能级的计算精度。以实验值为13 999.5 cm-1[2]的能级4f66s6p 9G1为例,Porsev[15]的计算值比实验值低2 466.5 cm-1,Zhou等[14]考虑上述电子关联效应,包含113 231个组态波函数时,计算值比实验值低912.5 cm-1;考虑291 689个组态波函数后,计算值比实验值仅高265.5 cm-1。与文献[15]的工作相比,Zhou等[14]的能级计算精度有了显著提高,但需要包含的组态波函数数目非常大,只能处理Sm原子的低激发态能级,要对Sm原子能级进行系统的理论研究非常困难。
对复杂原子体系的大量能级进行系统的精确计算,一种可行的方案是采用半经验的计算方法[16-17]。例如,Petit[16]利用实验能级拟合计算方法(简称拟合计算方法)成功地分析U原子0~24 000 cm-1范围内的155条能级,他们仅考虑了5f36d7s2和5f36d27s两个组态的能级,计算结果与实验值的平均偏差只有53 cm-1。本文采用拟合计算方法,对Sm原子精细结构能级进行系统的理论研究。
1 理论方法根据原子能量表达式,结合实验能级的拟合计算方法,是一种半经验的方法。该方法通过优化精细结构参量,使能级计算值与选取的实验值之间的平均偏差最小,从而得到所需的能级计算值。对于复杂原子体系,在Rydberg原子单位制下,非相对论加相对论修正的Hamiltonian量为
| $ H{\rm{ = }} - \sum\limits_i {\nabla _i^2 - \sum\limits_i {\frac{{2Z}}{{{r_i}}} + \sum\limits_{i > j} {\frac{2}{{{r_{ij}}}} + \sum\limits_i {{\xi _i}\left( {{r_i}} \right)\left( {{l_i} \cdot {s_i}} \right),} } } } $ | (1) |
其中:第1项为电子的动能项,第2项为核与电子间的库仑相互作用势能项,第3项为电子与电子的库仑能项,第4项是通过相对论修正引入的自旋-轨道相互作用项。
理论上求解薛定谔方程
| $ H\psi = E\psi , $ | (2) |
就能得到原子能级以及对应的原子波函数。拟合计算方法依据Slater-Condon理论,将未知原子波函数Ψk用一组已知的正交归一化的基函数Ψb(可用Hartree-Fock等方法计算得到)展开:
| $ {\psi ^k} = \sum\limits_b {Y_b^k{\psi _b}.} $ | (3) |
通过求解矩阵方程:
| $ \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{Y}}^k} = {\mathit{\boldsymbol{E}}^k}{\mathit{\boldsymbol{Y}}^k}. $ | (4) |
得到原子波函数。
对于轨道nili上电子占据数为wi的单组态(n1l1)w1(n2l2)w2…(nqlq)wq,它的Hamil-tonian量的矩阵元为
| $ \begin{array}{l} {\mathit{\boldsymbol{H}}_{ab}} = {\delta _{ab}}{E_{av}} + \sum\limits_{j = 1}^q {\left[ {\sum\limits_{k > 0} {{{\left( {{f_k}\left( {{l_j}{l_j}} \right)} \right)}_{ab}}{F^k}\left( {{l_j}{l_j}} \right) + } } \right.} \\ \left. {{{\left( {{d_j}} \right)}_{ab}}{\zeta _j}} \right] + \sum\limits_{i = 1}^{q - 1} {\sum\limits_{j = i + 1}^q {\left[ {\sum\limits_{k > 0} {{{\left( {{f_k}\left( {{l_i}{l_j}} \right)} \right)}_{ab}}{F^k}\left( {{l_i}{l_j}} \right) + } } \right.} } \\ \left. {\sum\limits_k {{{\left( {{g_k}\left( {{l_i}{l_j}} \right)} \right)}_{ab}}{G^k}\left( {{l_i}{l_j}} \right)} } \right]. \end{array} $ | (5) |
其中:Eav为组态平均能,Fk(ljlj)为同科电子间Slater直接积分,Fk(lilj)为非同科电子间Slater直接积分,Gk(lilj)为非同科电子间Slater交换积分,ζj是与自旋-轨道相互作用有关的径向积分。f、g、d是对应的角系数,它们只与相关波函数的角动量有关,是解析函数。Fk(ljlj)、Fk(lilj)、Gk(ljlj)、ζj都只与电子自旋-轨道波函数
| $ {\varphi _i}\left( {{r_i}} \right) = \frac{1}{{{r_i}}}{P_{{n_i}{l_i}}}\left( {{r_i}} \right){Y_{{l_i}{m_i}}}\left( {{\theta _i},{\varphi _i}} \right){\sigma _{{m_{{s_i}}}}}\left( {{S_{iz}}} \right) $ | (6) |
径向部分
拟合计算的精确度用平均偏差
| $ R = {\left( {\sum\limits_i^N {{{\left( {{E^i} - {T^i}} \right)}^2}/N} } \right)^{1/2}} $ | (7) |
来衡量,其中Ti为能级的实验值,Ei为计算值,N为所有(包括选取和没选择)的实验能级(样点)数目。更详细介绍见文献[18]第12章。
上述方法可以通过Cowan程序包[18]来实现。该程序包括RCN、RCN2、RCG、RCE等4个模块,其中RCE可用于能级的拟合计算。2012年,Kramida[19]发展了该程序,可以处理包含fn(n>4)电子占据的组态。本文利用Kramida程序包,对Sm原子的基态和激发态精细结构能级进行系统的理论研究。
2 Sm原子精细结构能级拟合计算结果与讨论我们首先研究Sm原子基组态[Xe]4f66s2的能级结构,得到参量与能级之间的关系,然后将这种规律应用于奇宇称组态4f66s6p+4f55d6s2以及偶宇称组态4f66s2+4f65d6s+4f66s7s能级的拟合计算。
2.1 基组态4f66s2的能级拟合计算L-S耦合表象下,Sm原子基组态4f66s2的态函数ψb可以表示为|f6aLSJM〉,其中a是为了区别同科电子允许的谱项中具有相同L、S值的谱项而引入的附加量子数,Hamiltonian量的矩阵元表达式为
| $ \begin{array}{l} \left\langle {{\psi _b}|\left. H \right|{\psi _b}^\prime } \right\rangle = {\delta _{bb'}}{E_{{\rm{av}}}} + {f_2}\left( {ff} \right){F^2}\left( {ff} \right) + \\ {f_4}\left( {ff} \right){F^4}\left( {ff} \right) + {f_6}\left( {ff} \right){F^6}\left( {ff} \right) + {d_f}\zeta \left( f \right). \end{array} $ | (8) |
其中参量Fk(ff)的系数
| $ {f_k}\left( {ff} \right) = {\delta _j}{f_k}\left( {L,S,a,a'} \right). $ | (9) |
δj表示只有当ψb和ψb′除附加量子数a和a′外其他量子数都对应相等时,fk(ff)才不为0,且fk(ff)的值仅与量子数L、S、a和a′有关。参量ζ(f)的系数df可简写为
| $ {d_f} = {\delta _{JM,J'M'}}{d_f}\left( {a,L,S,a',L',S',J} \right). $ | (10) |
其中δJM, J′M′表示只有当ψb和ψb′的量子数J、M和J′、M′对应相等时,df才不为0,且df的值与量子数a, L, S, a′, L′, S′, J都有关。Eav的系数只有当ψb和ψb′的所有量子数都对应相等时,才为1,否则为0。依据4f66s2组态各参量系数的特征,如果只考虑Hamiltonian矩阵主对角元项对能级精细结构的影响,可以得出以下结论:参量ζ(f)影响同一对称块的能级的相对大小,对称块是指L-S耦合表象下态函数只有总角动量J不同的态,如Sm原子基组态4f66s2中谱项为7FJ(J=0~6)的能级属于同一对称块;参量Fk(ff)影响不同对称块能级的相对大小;而参量Eav影响所有能级的绝对大小。
利用拟合计算方法得到精确的原子结构,最重要的是选择实验能级和优化参量。
首先,我们对4f66s27FJ对称块能级进行拟合计算。表 1给出选择不同能级实验值、优化不同参量的计算结果。为减少参量自由度,类似文献[20],拟合Ⅰ到Ⅳ都优化了参量Eav、Fk(ff)和ζ(f),其中Fk(ff)表示拟合计算过程中,保持F2(ff):F4(ff):F6(ff)的比例关系不变。拟合Ⅰ到Ⅲ中F2(ff):F4(ff):F6(ff)的比值由程序利用从头算方法(ab initio)直接计算得到,而拟合IV中的比值来源于氢原子的4f轨道波函数积分[20-21]。对比表 1中拟合Ⅰ、Ⅱ和Ⅲ的结果, 可以看出7F0-6这7条能级拟合计算值与实验值的平均偏差R1明显小于从头算(ab inito)的结果,且R1随着选取的能级实验值的数目增加而减少。对比拟合Ⅲ和Ⅳ可以发现F2(ff):F4(ff):F6(ff)的比值的选取,对平均偏差R1的影响较小,我们用从头算的计算精度与Conway[20]的在同一量级上。拟合Ⅴ将所有参量都设为自由可变量,对比拟合Ⅲ、Ⅳ,可以发现不固定F2(ff)、F4(ff)和F6(ff)间的比值,拟合计算结果更接近实验值。拟合Ⅴ的平均偏差R1比Conway[20]的小了约一个数量级。
|
|
表 1 实验、从头算及包含基组态4f66s2(7FJ)拟合计算能级 Table 1 Fine structures for the ground configurations from experiment, ab initio calculations, and fitting calculations for 4f66s2(7FJ) configurations |
表 1中基组态4f66s2 5D1-2这3条能级(有实验数据)的平均偏差R2的拟合计算值也明显小于从头算计算值;但R2的值都大于R1,这是由于我们没有选择4f66s2 5DJ对称块中的能级;因此R2与7FJ实验值的能级的选取以及拟合方式也没有明确的规律。
由Hamiltonian矩阵元表达式。式(8)可知,参量Eav、Fk(ff)(k=2、4、6)和ζ(f)对基组态4f66s2能级的影响不同。只拟合7FJ对称块的能级,可以有效地修正该对称块间的能级相对值,但对不同对称块(如5DJ)间能级相对值的修正相对有限。以拟合Ⅰ为例,虽然4f66s2 5D1-3这3条能级的计算值都比实验值小400 cm-1左右,但是能级间隙的计算值与实验值很接近,5D2和5D1、5D3和5D2的能级差的计算值分别为1 915.4 cm-1和2 305.7 cm-1,对应的实验值分别为1 949.7 cm-1和2 331.5 cm-1。参量ζ(f)影响同一对称块能级的相对大小,因此表 2中不同拟合计算得到参量ζ(f)的值变化不大,最小值为1 046.2 cm-1,最大值为1 069.0 cm-1,而其他参量值的变化相对较大。另外,从表 2中可以发现参量Eav和Fk(ff)(k=2、4、6)间存在负相关关系,Eav随着Fk(ff)的增大(减少)而减小(增大)。这是因为Eav和Fk(ff)(k=2、4、6)都影响能级的绝对值。
|
|
表 2 从头算以及包含基组态4f66s2(7FJ)拟合计算的参量值 Table 2 Parameters in ab initio calculations and different fitting calculations |
下面我们对基组态4f66s2 7FJ和5DJ两个对称块的能级同时进行拟合计算。表 3给出选取不同能级的实验值、优化不同参量的计算结果。与上面的计算类似,拟合Ⅵ到Ⅹ优化了参量Eav、Fk(ff)和ζ(f),拟合Ⅵ到Ⅸ中F2(ff):F4(ff):F6(ff)的比值由从头算方法(ab initio)得到,而拟合Ⅹ中的比值来源于氢原子的4f轨道波函数[21]积分。对比拟合Ⅵ到Ⅸ的计算结果可以发现:随着拟合能级数目的增加,平均偏差R1和R2都趋向于变小。对比拟合ⅡⅩ和Ⅹ可以发现它们的计算精度相当,F2(ff):F4(ff):F6(ff)的比值对平均偏差R1和R2的影响较小。拟合ⅡⅩ的R1比拟合Ⅹ的R1只大1.1 cm-1,而R2只小0.8 cm-1。拟合Ⅺ和Ⅻ将所有参量都设为自由可变量, 与拟合IIX、Ⅸ和拟合Ⅹ比较可以发现:增加参量自由度可以提高能级的计算精度,但未拟合实验值的能级的计算精度并不一定提高。例如,表 3中拟合Ⅹ的R1比拟合IIX的小,但是R2变大了。
|
|
表 3 实验及包含基组态4f66s2(7FJ,5DJ)拟合计算能级 Table 3 Fine structures for the ground configurations from experiment and fitting calculations for 4f66s2(7FJ, 5DJ) configurations |
对比表 3和表 1中R2的值,可以发现:选取包含基组态4f66s2 5DJ对称块能级的实验值,可以显著提高该对称块的计算精度。例如,表 1中拟合I和表中3拟合Ⅵ都拟合了7FJ对称块中7F0-2 3条能级的实验值,但拟合Ⅵ多拟合了一条4f66s2 5D1能级的实验值,R2由拟合Ⅰ的415.6 cm-1大幅度降为拟合Ⅴ的19.8 cm-1。
依据对Hamiltonian矩阵元的分析,Fk(ff)(k=2、4、6)影响基组态不同对称块能级的相对值,同时拟合基组态4f66s2 7FJ和5DJ的能级时,会对Fk(ff)(k=2、4、6)进行调整。对比表 2和表 4的不同拟合计算得到的参量值可以发现:固定F2(ff):F4(ff):F6(ff)的比值时,参量Eav、Fk(ff)(k=2、4、6)和ζ(f)的变化都较小,例如表 4中拟合Ⅵ到Ⅶ,Eav的变动范围为-6 176.7~-6 116.9 cm-1,F2(ff)的变动范围为82 335.1~82 410.0 cm-1,ζ(f)的变动范围为1 054.7~1 059.1 cm-1。不固定F2(ff):F4(ff):F6(ff)的比值时参量Eav、Fk(ff)(k=2、4、6)的变动较大,例如表 4中拟合Ⅺ和Ⅻ。
|
|
表 4 包含基组态4f66s2(7FJ,5D0J)拟合计算的参量值 Table 4 Parameters in different fitting calculations |
通过分析Sm原子基组态4f66s2能级的不同拟合计算结果,可以得出以下结论:
1)拟合计算时只需选取同一对称块的部分实验能级,就能有效提高该对称块中所有能级的计算精度。例如表 3中,拟合Ⅵ只选取了7FJ对称块中7F0-2,以及5DJ对称块中5D1的实验能级,但7F3,4和5D2,3的计算值与实验值的差异也都小于26 cm-1。
2)参量ζ(f)的值受Slater积分Fk(ff)(k=2、4、6)[20]和Eav的影响较小。例如,表 2中拟合Ⅰ和Ⅲ,Eav变动约2 500 cm-1,F2(ff)变动约4 000 cm-1,但参量ζ(f)只变动14.1 cm-1。
3)参量Eav和Fk(ff)(k=2、4、6)间存在负相关的变化规律。
4)增加参量自由度可以提高拟合了实验值的能级的计算精度。
5)验证了通过分析Hamiltonian矩阵对角元得出的结论:参量ζ(f)影响基组态4f66s2同一对称块的能级的相对大小;Fk(ff)(k=2、4、6)影响不同对称块能级的相对大小;Eav影响所有能级的绝对大小。
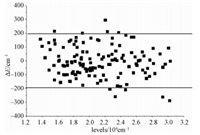
2.2 奇宇称(4f66s6p+4f55d6s2)能级拟合计算奇宇称组态4f66s6p和4f55d6s2的能级有较大重叠[2],组态间相互作用较强,需要同时拟合计算这2个组态的能级。对于这2个组态,Carlier等[22]计算的能级误差主要分布在±200 cm-1以内,部分能级的误差接近300 cm-1,见图 2。
|
Download:
|
|
图 2 组态4f6(7F)6s6p和4f5(6H, 6F)5d6s2精细结构能级拟合计算[22]的误差 Fig. 2 Differences in the fine structures between experiments and fitting calculations[22] for configurations 4f6(7F)6s6p and 4f5(6H, 6F)5d6s2 |
|
在他们的拟合计算中,只选择了4f6(7F)6s6p+4f5(6H、6F)5d6s2谱项,我们则同时考虑了4f66s6p+4f55d6s2所有的耦合谱项。依据基组态4f66s2能级拟合计算研究的结论,我们选取美国国家标准与技术研究院(NIST)已标识为4f66s6p和4f55d6s2组态的134条能级中的22条的实验值[2]进行拟合。选取拟合实验值能级的2个原则是:第一、自旋-轨道耦合参量ζ主要影响同一对称块的能级辟裂,每个组态至少有一个对称块需要包含多条参考实验能级,例如上面基组态中的4f66s2 7FJ对称块,以优化对应的ζ参量;第二、与库仑相互作用有关的参量,如Slater积分Fk、Gk等,主要影响不同对称块间的能级辟裂,因此每个对称块都要选择一条以上纯度高的能级的实验值,以优化这些参量。纯度高是指能级波函数展开式中,某一个谱项的系数比较大。
图 3给出了我们拟合计算奇宇称组态4f66s6p + 4f55d6s2能级的误差分布,它们主要集中在-200~150 cm-1, 只有个别能级的误差在300 cm-1左右。与Carlier等[22]相比,我们的计算结果更加接近实验值。因为他们只考虑了4f6(7F)6s6p和4f5(6H、6F)5d6s2类的谱项;但在我们的计算中,考虑了所有对称块,而且只拟合部分纯度较高、标识清楚的能级的实验值。与基组态4f66s2能级拟合计算结果类似,没有拟合实验值的能级也有较高的精度。例如,4f5(6F)5d6s2组态7DJ对称块,只参考了7D1能级的实验值;但该对称块能级的误差小于106 cm-1,相对误差也小于0.4%,见表 5。对于4f66s6p组态9GJ对称块,只选取了9G0, 4, 6的实验值,但该对称块所有能级的误差小于47 cm-1,相对误差小于0.4%,见表 6。
|
|
表 6 4f66s6p 9GJ对称块的计算结果 Table 6 Results for 4f66s6p 9GJ |
|
|
表 5 4f55d6s2 7DJ对称块的计算结果 Table 5 Results for 4f55d6s2 7DJ |

|
Download:
|
|
图 3 组态4f66s6p和4f55d6s2精细结构能级拟合计算的误差 Fig. 3 Differences in the fine structures between experiments and fitting calculations for configurations 4f6(7F)6s6p and 4f5(6H, 6F)5d6s2 |
|
NIST表中已标识的偶宇称组态4f66s2+4f65d6s2+4f66s7s的能级数比奇宇称能级数少,只有65条[2]。采用与2.2节相同的原则,我们选择其中17条实验能级进行拟合计算。由于偶宇称组态中包含基组态,计算结果误差较小,主要分布在-50~75 cm-1,只有6条能级的误差分布在-150~-50 cm-1,见图 4。与奇宇称类似,没有拟合实验值能级的计算值也很接近实验值。例如,对于4f65d6s组态7HJ对称块,只选取了7H2的实验值,但该对称块能级的误差小于36 cm-1,相对误差小于0.3%,见表 7。又如,4f66s7s组态9FJ对称块,只参考了9F1, 4, 7的实验值,但该对称块的其他能级的误差也小于10 cm-1,相对误差小于0.3%,见表 8。
|
|
表 7 4f65d6s 7HJ对称块的计算结果 Table 7 Results for 4f65d6s 7HJ |
|
|
表 8 4f66s7s 9FJ对称块的计算结果 Table 8 Results for 4f66s7s 9FJ |

|
Download:
|
|
图 4 组态4f66s2、4f65d6s和4f66s7s精细结构能级拟合计算的误差 Fig. 4 Differences in the fine structures between experiments and fitting calculations for configurations 4f66s2, 4f65d6s, and 4f66s7s |
|
最后,依据拟合计算结果,本文将文献[23]中测得的5条高激发态偶宇称能级标识为4f6(7F)6s7s 5F1-5,见表 9。这5条能级纯度高,最大谱项的占比都超过70%,而且能级计算值与实验值的差异比较小。其中实验值为31 246.2 cm-1的能级,NIST[2]也标识为4f6(7F)6s7s5F2谱项,其他能级目前未见文献对它们进行标识。当然,标识最终确定还需要结合实验上对能级g因子、同位素位移等物理量的测定。
|
|
表 9 文献[23]中4f6(7F)6s7s组态5FJ能级的标识 Table 9 Identification of 4f6(7F)6s7s (5FJ) configuration presental in Ref.[23] |
本文通过分析Sm基组态4f66s2的Hamiltonian矩阵元的特征,得到各参量对基组态4f66s2能级结构的影响规律,并得到具体拟合计算的验证。运用这些规律,对于奇宇称组态4f66s6p+4f55d6s2能级,本文利用22条实验能级,拟合计算得到134条较精确的计算值。对于偶宇称组态4f66s2+4f65d6s+4f66s7s能级,利用17条实验能级,得到了65条较精确的计算值。根据拟合计算结果,本文对文献[23]中5条偶宇称高激发态能级进行了谱项标识。
| [1] | Bünzli J C G. Lanthanide luminescence for biomedical analyses and imaging[J]. Chem Rev , 2010, 110 (5) :2729–2756. DOI:10.1021/cr900362e |
| [2] | Kramida A, Ralchenko Yu, Reader J, et al. NIST atomic spectra database (ver. 5.2) [DB/OL]. Gaithersburg: NIST, 2014 [2016-04-10]. http://physics.nist.gov/asd. |
| [3] | Jia L, Jing C, Zhou Z, et al. Studies of high-lying even-parity levels of Sm:energies and isotope shifts[J]. J Opt Soc Am B , 1993, 10 (8) :1317–1320. DOI:10.1364/JOSAB.10.001317 |
| [4] | Jayasekharan T, Razvi M A N, Bhale G L. Observation of new even-parity states of Sm I by resonance ionization mass spectrometry[J]. J Opt Soc Am B , 1996, 13 (4) :641–648. DOI:10.1364/JOSAB.13.000641 |
| [5] | Jayasekharan T, Razvi M A N, Bhale G L. Investigations of new high-lying even-parity energy levels of the samarium atom below its first ionization limit[J]. J Opt Soc Am B , 2000, 17 (9) :1607–1615. DOI:10.1364/JOSAB.17.001607 |
| [6] | Pulhani A K, Shah M L, Dev Vas, et al. High-lying even-parity excited levels of atomic samarium[J]. J Opt Soc Am B , 2005, 22 (5) :1117–1122. DOI:10.1364/JOSAB.22.001117 |
| [7] | Qin W J, Dai C J, Xiao Y, et al. Experi-mental study of highly excited even-parity bound states of the Sm atom[J]. Chin Phys B , 2009, 18 (8) :3384–3394. DOI:10.1088/1674-1056/18/8/044 |
| [8] | Pulhani A K, Shah M L, Gupta G P, et al. Measurement of total angular momentum values of high-lying even-parity atomic states of samarium by spectrally resolved laser-induced fluorescence technique[J]. Pramana J Phys , 2010, 75 (6) :1135–10139. DOI:10.1007/s12043-010-0196-3 |
| [9] | Li M, Dai C J, Xie J. Even-parity states of the Sm atom with stepwise excitation[J]. Chin Phys B , 2011, 20 (6) :063204. DOI:10.1088/1674-1056/20/6/063204 |
| [10] | Li M, Dai C J, Xie J. Photoionization spectra of even-parity states of Sm atom with multistepexcitation[J]. Quant Spectrosc Radiat Transfer , 2011, 112 (5) :793–799. DOI:10.1016/j.jqsrt.2010.11.005 |
| [11] | Zhao Y H, Dai C J, Ye S W. Study on even-parity highly excited states of the Sm atom[J]. J Phys B , 2011, 44 (19) :195001. DOI:10.1088/0953-4075/44/19/195001 |
| [12] | Shah M L, Sahoo A C, Pulhani A K, et al. Investigations of high-lying even-parity energy levels of atomic samarium using simultaneous observation of two-color laser-induced fluorescence and photoionization signals[J]. Eur Phys J D , 2014, 68 :235. DOI:10.1140/epjd/e2014-50076-8 |
| [13] | 杨騄, 戴长健, 赵红艳. 用光电离技术探测钐原子的奇宇称束缚激发态的光谱[J]. 物理学报 , 2013, 62 (5) :053201. |
| [14] | Zhou F Y, Qu Y Z, Li J G, et al. Multi-configuration Dirac-Hartree-Fock calculations of excitation energies, oscillator strengths, and hyperfine structure constants for low-lying levels of Sm I[J]. Phys Rev A , 2015, 92 (5) :052505. DOI:10.1103/PhysRevA.92.052505 |
| [15] | Porsev S G. Calculation of lifetimes of low-lying odd-parity levels of Sm[J]. Phys Rev A , 1997, 56 (5) :3535–3542. DOI:10.1103/PhysRevA.56.3535 |
| [16] | Petit A. Fine structure parametric analysis of the f3ds2+f3d2s configurations in U I[J]. Eur Phys J D , 1999, 6 (2) :157–170. |
| [17] | Stachowska E, Elantkowska M, Ruczkowski J. Reanalysis and semi-empirical predictions of the hyperfine structure of Eu I in the odd parity multi-configuration system[J]. Phys Scr , 2002, 65 (3) :237–247. DOI:10.1238/Physica.Regular.065a00237 |
| [18] | Cowan R D. The theory of aomic structure and spectra[M]. Los Angeles: University of California Press, 1981 . |
| [19] | Kramide A. A version of Cowan code package adapted for personal computers[CP/OL].[2016-04-08]. http://das101.isan.troitsk.ru. |
| [20] | Conway J G, Wybourne B G. Low-lying energy levels of lanthanide atoms and intermediate coupling[J]. Phys Rev , 1963, 130 (6) :2325–2332. DOI:10.1103/PhysRev.130.2325 |
| [21] | Judd B R, Lindgren I. Theory of zeeman effect in the ground multiplets of rare-earth atoms[J]. Phys Rev , 1961, 122 (6) :1802–1812. DOI:10.1103/PhysRev.122.1802 |
| [22] | Carlier P A, Blaise J, Schweighofer M G. Étude des configurations impaires 4f66s6p et 4f55d6s2 de Sm I[J]. J Phys (Paris) , 1968, 29 (8/9) :729–738. |
| [23] | 赵红艳. Sm原子束缚态和自电离态的光谱及其特征[D].天津:天津理工大学, 2011. |
 2017, Vol. 34
2017, Vol. 34 


