随着大数据时代的到来,数据在各领域逐渐成为研究热点,其中时间序列是一种应用非常广泛的数据类型.由于时间序列数据蕴含着丰富的信息,因此基于时间序列的预测已经引起了越来越多的关注.然而,事物状态的刻画往往需要多个维度共同确定,且各个维度之间存在一定的关联关系;因此,使用多维时间序列可以得到更多的信息[1-2],且现实场景中有很多多维时间序列数据,如金融数据[3]、气象数据[4-5]、医学数据[6-7]等.
时间序列预测是采用预测模型根据历史数据预测未来值.因此,多维时间序列预测是根据多维时间序列的历史值预测某目标维度的未来值.不同领域的方法都被用来解决时间预测问题.总体而言,已有的基于时间序列的预测主要分为以下两类.一类是以自回归移动平均模型(auto regression moving average,ARMA)和求和自回归移动平均模型(auto regressive integrated moving average model,ARIMA)为代表的基于统计的时间序列预测算法.ARMA模型主要适合线性平稳时间序列,ARIMA模型主要用来对差分平稳时间序列进行预测.这些都是线性模型.近些年关于这些传统的时间序列模型的改进也有很多[8-9].但由于现实世界的时间序列数据具有复杂性和随机性,很难通过线性模型进行准确的描述.另一类以神经网络、支持向量机等为代表的非线性时间序列预测模型开始发展.随着大数据时代的到来,数据挖掘和机器学习等算法得到了广泛的应用和发展,因此关于这类非线性时间序列预测模型的改进也越来越多.以上预测模型主要是基于单维时间序列的预测,但近些年来,针对多维时间序列的预测都有相应的改进[10-11].每个模型都有其缺点和优点,因而,组合预测模型成为一个重要的研究方向.
本文将k-NN和BP神经网络模型组合进行多维时间序列预测.首先通过k-NN从训练数据集中搜索与测试数据集中的样本的k个近邻,然后得到预测维度的预测值;其次通过BP神经网络模型得到另一个预测值;最后,将这两个预测结果作为输入,再次采用BP神经网络模型得到最终的预测结果.
1 相关工作 1.1 多维时间序列多维时间序列X是一组维度xi (i=1,2,3,…,m)在一系列连续时刻tj (j=1,2,3,…,n)取得的有序观测值的集合.时间序列各时间间隔可以相同,也可以不同,目前研究的主要是相同时间间隔的时间序列,即Δt=tj+1-tj (j=1,2,3,…,n-1)为定值.为便于描述,将tj记为j,即第j时刻.当m=1时,X为单维时间序列.当m>1时,即时间序列的维度数大于1,称X为多维时间序列.则X可表示为一个m×n的矩阵,记为
| $X=\left( \begin{matrix} {{x}_{11}} & \ldots & {{x}_{1n}} \\ \vdots & \ddots & \vdots \\ {{x}_{m1}} & \cdots & {{x}_{mn}} \\ \end{matrix} \right),$ | (1) |
式中,xij表示第i个维度在第j时刻的观测值,且X的每一行都是一个单维时间序列.
通过滑动窗口方法将X转换为一个新的数据集D.设滑动窗口的长度为h+p.则D={X1,X2,…,XL},(L=n-h-p+1),且Xj为
| $X=\left( \begin{matrix} {{x}_{1j}} & \ldots & {{x}_{1\left( j+h+p-1 \right)}} \\ \vdots & \ddots & \vdots \\ {{x}_{mj}} & \cdots & {{x}_{m\left( j+h+p-1 \right)}} \\ \end{matrix} \right),\left( 1\le j\le n-h-p+1 \right).$ | (2) |
Xj的前h列为训练模型的输入,本文记为inwj.Xj的后p列为预测模型的输出,本文记为outwj.记Xij为Xj的第i行,表示时间序列的第i个维度,并且inwij和outwij分别作为关于Xij的训练模型的输入输出.即多维时间序列预测模型为
| $\begin{align} & x{{\prime }_{i(j+h+l)}}={{f}_{il}}(in{{w}_{j}}),(1\le i\le m,1\le j\le \\ & n-h-p+1,0\le l\le p-1). \\ \end{align}$ | (3) |
本文,设第m个维度为目标预测维度.下面主要介绍已有的预测方法.
1.2 多维时间序列预测模型随着数据挖掘和机器学习技术的发展和数据积累,无论从技术还是从数据获取方面,都为多维时间序列预测提供了可能.基于多维时间序列的预测研究逐渐成为一个研究趋势.由于多维时间序列具有数据量大、高维度等特征[12],基于多维时间序列的预测更加复杂和困难,组合预测模型成为解决该问题的一个重要研究方向.
文献[10]使用奇异值分解(singular value decomposition,SVD)抽取特征,然后使用神经网络进行预测.Han等[13]使用主成分分析(principle component analysis,PCA)去抽取有价值的信息进而降低维度,然后采用Elman神经网络进行预测.Cai等[14]提出改进的支持向量回归(support vector regression,SVR)方法进行多维时间序列预测.文献[15]将改进的径向基(radial basis function,RBF)神经网络用于多维时间序列预测.曹新莉和王树朋[16]通过对原始风电功率序列进行处理得到重构相空间,然后利用重构相空间中预测点的近邻点建立BP神经网络预测模型.韩敏等[17]提出一种基于快速子空间分解方法的回声状态网络预测模型.陈飞彦等[18]针对物联网数据的异常或缺失问题,首先使用k近邻算法对数据进行估值或替换等预处理,并进行初步预测,然后对预处理后的数据使用BP神经网络预测,综合BP神经网络和k-NN的预测结果给出最终结论.此外文献[18]是针对类别属性预测的,组合BP神经网络和k-NN的预测结果时主要采用的是线性组合方式.由于多维时间序列的复杂性,很难综合所有相关维度进行预测.目前大多已有的多维时间序列预测模型采用单一模型进行预测,基于多维时间序列的组合模型研究较少.而基于单维时间序列的组合预测模型中,郑为中和史其信[19]利用贝叶斯算法为分别采用BP神经网络和RBF神经网络模型的预测结果计算权重,将这两个预测结果进行线性组合得到最终的预测结果;秦大建和李志蜀[20]利用RBF神经网络将指数平滑预测方法和神经网络预测方法进行组合;周芳[21]用k-NN找出历史数据中相似的最近邻,并使用神经网络寻找这些近邻的最优权重,得到最终的预测结果;文献[22-23]中,k-NN被用来有效减少训练数据集数据量,采用k-NN为测试集中的每个样本选择最相似的近邻,然后分别采用LS-SVM和神经模糊系统为每个测试样本训练预测模型.综上,由于神经网络可以很好地处理非线性模型,因此,各种神经网络模型被用来进行预测.k-NN算法的一个优势是,历史数据集越大,搜索到的近邻越相似.为了充分利用历史数据和集成多个算法优势,本文采用基于k-NN和BP神经网络的组合模型进行预测.
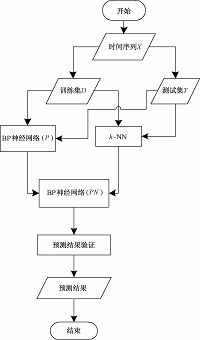
2 本文方法 2.1 本文模型原理研究中发现,单一预测模型通常在某一时期或对某类特征的数据有较好的预测表现,即每种预测模型都有其适用范围.因此,如果选取多个模型,每个模型在某一时段都有较佳的预测效果,将这些模型组合起来用于整体区间的预测,效果应该更佳,即组合预测模型.则组合预测模型就是使用多个模型,以某种方式集成它们的特征,最终得到较佳的预测结果.本文提出的组合预测模型使用了k-NN和BP神经网络模型,为了将得到的两个预测结果进行合理的组合,采用BP神经网络预测模型进行非线性组合,即通过BP神经网络模型训练权重,得到最佳的组合.在组合时,将上述的两个预测结果作为输入,使用BP神经网络进行模型训练.本文提出的模型框架如图 1所示.
|
Download:
|
|
图 1 本文模型框架 Fig. 1 Model framework of the proposed method |
|
如图 1所示,本文提出的模型步骤如下:
1) 采用滑动窗口方法将多维时间序列X进行转换,并分为训练集D和测试集T.
2) 采用k-NN方法,在训练集D中找到k个近邻.每完成一次搜索,将该样本加入搜索数据集中.
3) 使用BP神经网络训练基于训练数据集D的预测模型,记该神经网络模型为P.
4) 将从2) 和3) 得到的预测值作为输入,真实值作为输出,训练BP神经网络模型,记该神经网络模型为PN.
5) 将测试数据集T中的每个样本代入k-NN和模型P,得到对应的预测值.
6) 将从5) 得到的临时预测结果作为输入,从PN模型得到预测结果.
7) 根据已有规则或专家建议,如边界限制等,对从6) 得到的预测结果进行验证和修改,得到最终的预测结果.
8) 结束.
多维时间序列数据来自于真实世界的应用,因此每个维度都是具有物理意义的.根据经验或专家建议,可以得到一些规则,如维度的边界限制,即时间序列维度的取值范围是某一合理的区间.使用这些规则对预测结果进行进一步调整,可有效提高该模型的可信度.关于本文结合多维时间序列进行k-NN预测的模块和BP神经网络预测的模块等下面将有详细介绍.此外,本文提出的方法,有一些参数需要初始化,如inw的长度h、outw的长度p和k-NN方法中的参数k等.这些参数的确定将结合经验、专家建议和实验等进行确定.实验部分将对参数的确定详细介绍.
2.2 k-NN预测模块k-NN是一种基于类比学习的方法.即,通过比较一个给定的测试样本和训练样本的相似性.k-NN可以通过返回k个近邻的平均值进行回归预测.本文采用k个近邻的返回值进行k-NN方法的预测.
k-NN是基于相似性搜索的预测方法.为了度量样本之间的相似性,常使用欧式距离进行度量.然而,一方面,随着时间的变化,间隔时间较长的数据间往往会出现整体缩放的现象,为了降低由于数据缩放等对相似性度量带来的影响,相似性度量前需要进行数据标准化.另一方面,由于不同维度间纲量的差异,若不进行数据标准化,取值范围较大的维度的差异会影响取值范围较小的维度的相似性度量效果.因此,本文采用Min-Max数据标准化方法,将各维度取值都映射到区间[0,1].设训练数据集D的时间戳是从1到TL,则D的第j个样本为Xj,(1≤j≤TL),如(2)所示,inwj=(X1j,…,Xmj)T.inwj数据标准化到区间[0,1]后,有:
| $inw{{\prime }_{j}}=\left( \begin{matrix} x{{\prime }_{1j}} & \ldots & x{{\prime }_{1(j+h-1)}} \\ \vdots & \ddots & \vdots \\ x{{\prime }_{mT}} & \cdots & x{{\prime }_{m(T+h-1)}} \\ \end{matrix} \right),$ | (4) |
其中,
| $\begin{align} & x{{\prime }_{i(j+q)}}=\frac{{{x}_{i(j+q)}}-{{\min }_{in{{w}_{ij}}}}}{{{\max }_{in{{w}_{ij}}}}-{{\min }_{in{{w}_{ij}}}}}, \\ & \left( 1\le i\le m,0\le q\le h-1 \right). \\ \end{align}$ | (5) |
式中,mininwij和maxinwij分别为inwij的最小值和最大值.
对于一个给定的测试样本inwT,起始时间点为T,长度为h,数据标准化后,有:
| $inw{{\prime }_{j}}=\left( \begin{matrix} x{{\prime }_{1T}} & \ldots & x{{\prime }_{1(T+h-1)}} \\ \vdots & \ddots & \vdots \\ x{{\prime }_{mT}} & \cdots & x{{\prime }_{m(T+h-1)}} \\ \end{matrix} \right),$ | (6) |
其中,
| $\begin{align} & x{{\prime }_{i(T+q)}}=\frac{{{x}_{i(T+q)}}-{{\min }_{in{{w}_{iT}}}}}{{{\max }_{in{{w}_{iT}}}}-{{\min }_{in{{w}_{iT}}}}}, \\ & \left( 1\le i\le m,0\le q\le h-1 \right). \\ \end{align}$ | (7) |
式中,mininwiT和maxinwiT分别为inwiT的最小值和最大值.
然后计算inwT和每个训练集中样本的欧式距离,记为Dis(j,T),则
| $Dis\left( j,T \right)=\sum\limits_{q=0}^{h-1}{\sqrt{\sum\nolimits_{i=0}^{m}{{{\left( x{{\prime }_{i(j+q)}}-x{{\prime }_{i(T+q)}} \right)}^{2}}}}}.$ | (8) |
由于不同维度对目标预测维度的影响不同,在距离度量时,为不同维度加个权重,因此,式(8)转化为:
| $Dis\left( j,T \right)=\sum\limits_{q=0}^{h-1}{\sqrt{\sum\nolimits_{i=0}^{m}{{{w}_{i}}{{\left( x{{\prime }_{i(j+q)}}-x{{\prime }_{i(T+q)}} \right)}^{2}}}}}.$ | (9) |
其中,wi为第i个维度的权重.
经过相似性搜索,与测试样本最相似的k个样本被找到,则对应的k个outw中的值可用来预测.假设,第j个训练样是第T个测试样本的近邻.由于inwT和inwj经过标准化后相似,则对应的outw数据标准化后也相似.因此,为了得到预测值,outw也要进行数据标准化.
| $\begin{align} & x{{\prime }_{i(j+q)}}=\frac{{{x}_{i(j+q)}}-{{\min }_{in{{w}_{ij}}}}}{{{\max }_{in{{w}_{ij}}}}-{{\min }_{in{{w}_{ij}}}}}, \\ & \left( 1\le i\le m,h\le q\le p+h-1 \right) \\ \end{align}$ | (10) |
| $\begin{align} & x{{\prime }_{i(T+q)}}=\frac{{{x}_{i(T+q)}}-{{\min }_{in{{w}_{iT}}}}}{{{\max }_{in{{w}_{iT}}}}-{{\min }_{in{{w}_{iT}}}}}, \\ & \left( 1\le i\le m,h\le q\le p+h-1 \right) \\ \end{align}$ | (11) |
因为outwj≈outwT,所以x′i(j+q)≈x′i(T+q),即
| $\frac{{{x}_{i(j+q)}}-{{\min }_{in{{w}_{ij}}}}}{{{\max }_{in{{w}_{ij}}}}-{{\min }_{in{{w}_{ij}}}}}\approx \frac{{{x}_{i(T+q)}}-{{\min }_{in{{w}_{iT}}}}}{{{\max }_{in{{w}_{iT}}}}-{{\min }_{in{{w}_{iT}}}}}$ | (12) |
转化为
| ${{x}_{i(T+q)}}=\frac{{{x}_{i(j+q)}}-{{\min }_{in{{w}_{ij}}}}}{{{\max }_{in{{w}_{ij}}}}-{{\min }_{in{{w}_{ij}}}}}\left( {{\max }_{in{{w}_{iT}}}}-{{\min }_{in{{w}_{iT}}}} \right)+{{\min }_{in{{w}_{iT}}}}.$ | (13) |
式(13)是经过k-NN方法后xi(T+q)的一个预测值.当k≥2时,如(13)所示的k个预测值的平均值作为最终的预测值.设inwj1,…,inwjk为inwT的k个近邻,目前使用比较广泛的最终预测值的计算方法有算术平均值预测和带权重平均值预测.算术平均值预测的表示形式为
| ${{{\hat{x}}}_{i(T+q)}}=\frac{\sum\limits_{c=1}^{k}{{{x}_{i(T+q)}}_{jc}}}{k},$ | (14) |
式中,xi(T+q)jc是来自Xi(jc)的一个预测值.
对带权重的平均值预测,权重可以通过多种方式进行设置,由于与测试样本越相似,权重应该越高,本文采用以下方式:
| ${{x}_{i(T+q)}}=\sum\limits_{c=1}^{k}{{{w}_{jc}}{{x}_{i(T+q)}}_{jc}},$ | (15) |
式中,wjc为
| ${{w}_{jc}}=\frac{Dis{{\left( jc,T \right)}^{-1}}}{\sum\limits_{c=1}^{k}{Dis{{\left( ja,T \right)}^{-1}}}}.$ | (16) |
在k-NN方法中,参数k值的选择对结果会产生重大的影响.如果k值较小,“学习”的近似误差会减少,但预测结果对近邻的实例点非常敏感.如果k值较大,可以减少学习的估计误差,但学习的近似误差会增加,即不太相似的样本也对预测起作用,使预测误差变大.本文将根据历史数据具体情况和实验结果比较,选择较佳的k取值.
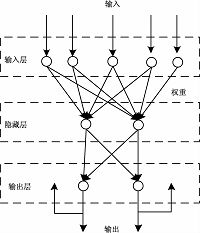
2.3 BP神经网络预测模块近年来,神经网络已经应用于多个领域.由于现实世界系统的动态性和复杂性,很难用确定的线性的函数进行准确的描述,因此传统的时间序列预测方法具有局限性,但神经网络可以解决该问题.本文使用BP神经网络进行两次预测,一是根据多维时间序列数据进行预测得到临时预测结果,二是将临时预测结果作为输入,进一步组合得到最终的预测结果.其结构图如图 2所示.
|
Download:
|
|
图 2 BP神经网络模型结构 Fig. 2 BP neural network model structure |
|
从图 2可知,BP神经网络有3层,包括输入层、隐藏层和输出层.隐藏层的层数可以大于1,但随着层数的增加,训练也会更加复杂.BP神经网络的训练过程如下:
1) 原始数据收集和预处理,如数据标准化.
2) 设计网络拓扑结构,包括隐藏层层数、输入结点数、隐藏层节点数和输出层节点数等.
3) 将1) 处理后的数据集分为训练集和测试集.
4) 设计训练算法训练BP神经网络模型.
5) 结合给定的误差评估BP神经网络模型的性能.当训练次数达到给定的最大训练次数,跳到6) .如果误差大于给定的误差阈值,转至4) ;否则,转至6) .
6) 将测试数据集导入满足条件的BP神经网络预测模型,得到相应的预测结果.
本文假设第m个维度为目标预测维度,使用inwj 和outwmj作为一组输入输出.此外,训练算法采用Levenberg-Marquadt算法.
2.4 组合预测模块组合预测方法是指将来自M个不同方法的预测结果{x1,x2,…,xM},按照一定的方式进行组合,进而得到最终的预测结果.目前常用的组合预测方法是基于线性的组合预测方法,即
| $\hat{x}=\sum\limits_{i=1}^{M}{{{w}_{i}}{{x}_{i}}},\left( 其中,\sum\limits_{i=1}^{M}{{{w}_{i}}=1} \right),$ | (17) |
式中,${\hat{x}}$为组合预测结果,wi为第i种方法预测结果的权重.
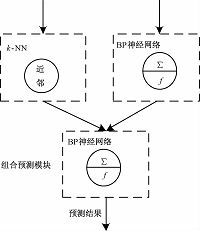
基于线性组合的预测方法,常见的权重系数选取方法有算术平均法、最优加权法、标准差法等,但这些方法的计算量都很大,而且效果欠佳.为了充分利用来自不同方法的预测结果,保持预测准确度的稳定性,达到最优的组合效果,本文采用了基于BP神经网络的非线性组合方法,利用BP神经网络训练得到最佳权重.如图 3所示.当k-NN预测模型和BP神经网络预测模型完成之后,在模型训练阶段,将得到的两组预测结果作为输入,真实值作为输出,再次利用BP神经网络模型,得到模型PN.在预测阶段,将k-NN和模型P得到的预测结果加载到模型PN,得到最终的预测结果.
|
Download:
|
|
图 3 组合预测模块 Fig. 3 The combined prediction module |
|
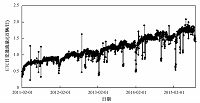
本文实验使用的数据是高速公路某ETC车道日交通流量的真实数据,包括2011年2月至2015年8月共4年1600多个日期的数据,ETC日交通流量如图 4所示,该站ETC交通流量总体呈波动上升趋势,在该图中,存在部分离群值,与其他时段交通量存在明显差异,这些特殊时段大多为法定节假日和特殊天气(如雨雪天气)日.因此,多维时间序列数据集还包括ETC交通流量的影响因素数据,即在此期间的法定节假日数据、高速公路免费数据以及每天的天气数据等.多维时间序列数据集各维度如表 1所示.本文实验中,2015年前的数据作为训练数据,2015年的数据作为测试数据.
|
Download:
|
|
图 4 高速公路ETC车道日交通流量时间序列图 Fig. 4 Time series diagram of highway ETC lane traffic flow |
|
|
|
表 1 多维时间序列ETC交通流量数据集 Table 1 Multi-dimensional time series ETC traffic flow dataset |
为评估本文方法的性能,本文进行了一系列实验比较本文预测方法和k-NN和BP神经网络预测模型.本文记基于多维时间序列的k-NN方法,采用式(14)进行预测的方法为knn1,采用式(15)进行预测的方法为knn2;基于单维时间序列的k-NN方法,采用式(14)进行预测的方法为knn3,采用式(15)进行预测的方法为knn4.本文根据文献[21]基于单维时间序列预测的算法思想,采用本文基于多维时间序列的k-NN方法得到k个近邻,然后使用BP神经网络训练得到最优的组合权重,本文记此方法为BP_kNN.本文对采用式(17)线性组合,且权重取值方式为算术平均的方法记为kNN_BP_S.
此外,为了能评价预测实验结果,本文采用相对误差(relative error,RE)和平均绝对相对误差(mean absolute relative Error,MARE)两个性能指标:
| $RE\left( t \right)=\frac{{{x}_{t}}-{{{\hat{x}}}_{t}}}{{{x}_{t}}},$ | (18) |
其中,xt是真实值,${{{\hat{x}}}_{t}}$是预测值,RE(t)主要用来描述t时刻的预测效果.
| $MARE=\frac{1}{N}\sum\limits_{t=1}^{N}{\left| RE\left( t \right) \right|}.$ | (19) |
式中,N表示预测样本总数,MARE是用来描述总体预测效果.
3.3 实验结果与分析据上所述,本文模型需要确定一些参数取值.根据经验和专家建议,各参数的取值范围如表 2所示.
|
|
表 2 参数取值范围 Table 2 Value ranges for parameter tuning |
当h=8,p=1时,比较不同k值的预测结果,结果如表 3所示.通过比较knn1、knn2和knn3、knn4,发现采用多维时间序列的预测结果的MARE比单维时间序列的小,即表明考虑的其他维度对目标预测维度的影响可提高预测效果.通过比较knn1和knn2,knn3和knn4发现,采用带权重的式(15)预测效果优于式(14),且随着k的增加,knn2和knn4预测结果的MARE变化较慢.因为k越大,不相似的近邻被用来预测,但其权重较小,对预测结果的影响也小.因此,本文选择knn2,取k=3,对应的MARE为5.22%.
|
|
表 3 不同方法和k预测的MARE Table 3 MARE values predicted using different methods with different k values |
对BP神经网络预测模块和组合预测模块采用的BP神经网络模型,各参数设置为隐藏层为1层,隐藏层结点为5,对k-NN模块的参数k取3,h =8,p =1.交通流量预测结果验证模块,根据ETC交通流量的数据情况以及相关经验,设ETC交通流量的取值范围为[0,2max],其中max为已知交通流量数据的最大值.当组合预测模块预测的交通流量预测值不在该范围时,用该预测时间点前h个历史值的均值替换该预测值.knn2、BP神经网络、BP_kNN、kNN_BP_S和本文方法预测结果的MARE如表 4所示.从表中可以看出,本文方法的MARE低于其他几种方法;对比knn2、BP神经网络和kNN_BP_S、本文方法,发现将knn2和BP神经网络进行组合,可有效提高预测效果;对比knn2和BP_kNN、kNN_BP_S和本文方法,发现采用BP神经网络训练的权重,MARE更小,也体现了采用BP神经网络训练权重的意义.因此,从整体意义上,本文方法具有较好的预测效果.本文方法的预测结果和真实结果如图 5所示.
|
|
表 4 不同方法的MARE Table 4 Performance comparison in terms of MARE % |

|
Download:
|
|
图 5 本文方法预测值与真实值比较图 Fig. 5 Comparison between the predicted results and the real values |
|
从图 5可以看出,本文预测模型误差较小,仅有少量点误差较大.为了进一步比较本文组合方法的组合预测效果,对所有预测值进行绝对相对误差统计,即|RE|,统计结果表 5所示.从表 5可以看出,本文方法的预测效果更好,且综合了k-NN和BP神经网络的优点.且本文方法90%以内的预测时间点的绝对相对误差都在10%以内,仅有少量的预测结果绝对相对误差大于20%.
|
|
表 5 预测误差统计结果 Table 5 Statistic results of the prediction errors |
本文提出一种基于k-NN和BP神经网络的多维时间序列组合预测模型,结合了k-NN预测稳定性和BP神经网络非线性预测的优点.此外添加预测结果验证模块,利用已知规则和专家建议,对不合理预测结果进行调整,进一步提高了模型的预测效果.利用ETC车道交通流量真实数据进行验证,实验表明,本文模型在整体预测性能上具有较低的MARE,即优于单一预测模型.同时90%的预测结果的绝对相对误差不大于10%,仅有少量的预测结果大于20%,满足应用需求.
| [1] | Cao L, Mees A, Judd K. Dynamics from multivariate time series[J]. Physica D Nonlinear Phenomena , 1998, 121 (1) :75–88. |
| [2] | Jamshidi A A, Kirby M J. Modeling multivariate time series on manifolds with skew radial basis functions[J]. Neural Computation , 2011, 23 (1) :97–123. DOI:10.1162/NECO_a_00060 |
| [3] | Islam F, Shahbaz M, Ahmed A U, et al. Financial development and energy consumption nexus in Malaysia:a multivariate time series analysis[J]. Economic Modelling , 2013, 30 (1) :435–441. |
| [4] | 陈晓云, 吴本昌, 韩海涛. 基于多维时间序列挖掘的降雨天气模型研究[J]. 计算机工程与设计 , 2010, 31 (4) :898–902. |
| [5] | Bueno L, Costa P, Mendes I, et al. Evolving ensemble of fuzzy models for multivariate time series prediction[C]//Fuzzy Systems (FUZZ-IEEE), 2015 IEEE International Conference on. IEEE, 2015:1-6. |
| [6] | Zhang X L, Begleiter H, Porjesz B, et al. Event related potentials during object recognition tasks[J]. Brain Research Bulletin , 1995, 38 (6) :531–538. DOI:10.1016/0361-9230(95)02023-5 |
| [7] | Jones S S, Evans R S, Allen T L, et al. A multivariate time series approach to modeling and forecasting demand in the emergency department[J]. Journal of Biomedical Informatics , 2009, 42 (1) :123–139. DOI:10.1016/j.jbi.2008.05.003 |
| [8] | Wang H R, Wang C, Lin X, et al. An improved ARIMA model for hydrological simulations[J]. Nonlinear Processes in Geophysics Discussions , 2014, 1 (1) :841–876. DOI:10.5194/npgd-1-841-2014 |
| [9] | 黄雁勇, 王沁, 李裕奇. ARMA模型参数估计算法的改进[J]. 统计与决策 , 2009 (16) :7–9. |
| [10] | Han M, Fan M. Multivariate time series prediction by neural network combining SVD[C]//Systems, Man and Cybernetics, 2006. SMC'06. IEEE International Conference on. IEEE, 2006:3884-3889. |
| [11] | Han M, Wang X. Multi reservoir support vector echo state machine for multivariate time series prediction[C]//Proceedings of the 2013 IEEE International Conference on Systems, Man, and Cybernetics. IEEE Computer Society, 2013:983-987. |
| [12] | Fu T C. A review on time series data mining[J]. Engineering Applications of Artificial Intelligence , 2011, 24 (1) :164–181. DOI:10.1016/j.engappai.2010.09.007 |
| [13] | Han M, Fan M, Xi J. Study of nonlinear multivariate time series prediction based on neural networks[C]//Advances in Neural Networks-ISNN 2005. Springer Berlin Heidelberg, 2005:618-623. |
| [14] | Cai Y, Wang H, Ye X, et al. Multivariate Time Series Prediction Based on Multi-Output Support Vector Regression[C]//The Seventh International Conference on Intelligent System and Knowledge Engineering, ISKE 2012/The 1st International Conference on Cognitive System and Information Processing, CSIP 2012.2012:385-395. |
| [15] | Xi J H, Wang H D, Jiang L Y. Multivariate time series prediction based on a simple RBF network[J]. Advanced Materials Research , 2012, 566 :97–102. DOI:10.4028/www.scientific.net/AMR.566 |
| [16] | 曹新莉, 王树朋. 基于多维时间序列和BP神经网络的短期风电功率预测[J]. 陕西电力 , 2014, 42 (4) :19–23. |
| [17] | 韩敏, 许美玲, 王新迎. 多元时间序列的子空间回声状态网络预测模型[J]. 计算机学报 , 2014, 37 (11) :2268–2275. |
| [18] | 陈飞彦, 田宇驰, 胡亮. 物联网中基于KNN和BP神经网络预测模型的研究[J]. 计算机应用与软件 , 2015 (6) :127–129. |
| [19] | 郑为中, 史其信. 基于贝叶斯组合模型的短期交通量预测研究[J]. 中国公路学报 , 2005, 18 (1) :85–89. |
| [20] | 秦大建, 李志蜀. 基于神经网络的时间序列组合预测模型研究及应用[J]. 计算机应用 , 2006, 26 (B06) :129–131. |
| [21] | 周芳. 基于KNN-ANN算法的边际电价预测[J]. 计算机工程 , 2010, 36 (11) :188–189. |
| [22] | Huang Z, Shyu M L. k-NN based LS-SVM framework for long-term time series prediction[C]//Information Reuse and Integration (IRI), 2010 IEEE International Conference on. IEEE, 2010:69-74. |
| [23] | Wei C C, Chen T T, Lee S J. k-NN based neuro-fuzzy system for time series prediction[C]//201314th ACIS International Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing (SNPD). IEEE Computer Society, 2013:569-574. |
 2016, Vol. 33
2016, Vol. 33 


