合成孔径激光雷达(SAL)结合合成孔径技术和激光波长短的特点，在超高分辨率观测领域发展前景广阔^[1]，但也存在数据量巨大的问题.文献[2]给出机载SAL系统参数：快时间采样率4 GHz，重复频率大于80 kHz.如此高的二维采样率导致的大数据量，给回波存储和成像处理都带来了困难.

由于激光波束窄，SAL成像场景幅宽小，使用LFM信号时，去斜接收可降低AD采样率和成像数据量^[3].模拟去斜需要复杂的延时控制电路，且采样率受延时误差影响，为简化系统并进一步降低采样率，本文将低采样率数字去斜技术^[4]应用于SAL.

1 采样率分析

为降低峰值功率，机载SAL通常采用线性调频连续波(LFMCW)体制，这为使用数字去斜提供了条件，依据文献[2]，本文确定的机载SAL系统参数如表 1所示.为避免方位多普勒模糊，本文采用100 kHz的高重频，对应10 μs的扫频周期；由于激光距离向波束较窄，场景幅宽远小于扫频周期对应的宽度，在3 km范围，存在的距离模糊可自动去除.

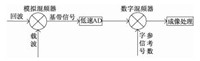
图 1给出低采样率数字去斜的原理框图.文献[4]从原理上证明并仿真验证了，若采样率大于模拟去斜时场景幅宽对应的谱宽，使用低采样率数字去斜技术，可获得全分辨率的脉压结果.

模拟去斜时，采样率的选择应综合考虑场景幅宽、延时误差和信号非线性失真的影响，采样率应满足

${{f}_{s}}\ge \gamma \left( \frac{2\Delta {{R}_{w}}}{C}+\frac{2\Delta {{R}_{\varepsilon }}}{C} \right)+\Delta {{f}_{s}},$

(1)

其中，f_s为快时间采样率，γ为发射LFM信号的调频率，ΔR_w为场景幅宽，ΔR_ε为最大延时误差(本文中延时用斜距表示)，Δf_s为因信号非线性失真增加的采样率，一般比较小.

低采样率数字去斜时，由于去斜操作由后续信号处理实现，生成回波矩阵前，可由回波数据估计延时范围，所以采样率的选择只需要考虑场景幅宽和信号非线性的影响，采样率应满足

${{f}_{s}}\ge \gamma \frac{2\Delta {{R}_{w}}}{C}+\Delta {{f}_{s}}.$

(2)

由表 1给出的系统参数，ΔR_ε=150 m，ΔR_w=15 m，若模拟去斜，采样率应大于440 MHz；若低采样率数字去斜，采样率大于40 MHz即可.考虑到延时估计误差以及信号非线性的影响，本文将快时间采样率设置为100 MHz.显然，将低采样率数字去斜应用于SAL可进一步降低系统采样率.

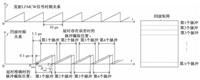
2 延时估计和回波矩阵形成

LFMCW体制下，信号的收发连续进行，需要对连续的回波信号进行裁剪，获得等效的脉冲信号，然后形成二维回波矩阵以进行后续的成像处理.信号裁剪的时序关系如图 2所示，假设场景最小延时为R_min，最大延时为R_max，回波矩阵中每个脉冲的起止时间应为单个扫频周期信号发射后$\frac{2{{R}_{\max }}}{C}$到$\frac{2{{R}_{\min }}}{C}+{{T}_{p}}$，T_p为扫频周期.

回波信号的延时范围可由载机和场景的GPS位置信息换算得到，其误差通常较小，但是由于飞机高度和横滚角变化，机载SAL获取数据时，回波延时最大可能存在150 m左右的误差，对应1 μs的时序错位.SAL重复频率高，扫频周期较短，延时误差会造成较大的能量损失.如图 2所示，由表 1给出的系统参数，若延时精确已知，能量损失仅来自场景幅宽，为0.1 μs/10 μs=1%；若存在150 m的延时误差，能量损失增大为1.1 μs/10 μs=11%.

为降低能量损失，在形成回波矩阵前，需取同一扫频周期信号的回波去斜脉压以进行延时估计.设由GPS数据换算得到的延时为[R, R+ΔR_w]，最大延时误差为ΔR_ε，考虑极限情况：若延时提前ΔR_ε，那么延时区间[R+ΔR_ε+ΔR_w, R+ΔR_ε+$\frac{{{T}_{p}}C}{2}$]中的信号必然是同一扫频周期信号的回波；若延时滞后ΔR_ε，那么延时区间[R－ΔR_ε+ΔR_w, R－ΔR_ε+$\frac{{{T}_{p}}C}{2}$]中的信号必然是同一扫频周期信号的回波；准确延时未知，但2个区间交集[R+ΔR_ε+ΔR_w, R－ΔR_ε+$\frac{{{T}_{p}}C}{2}$]中的信号必然是同一扫频周期信号的回波，且包含场景中所有散射点的信息，取该段回波去斜脉压即可估计出延时范围.根据该延时范围，将接收到的连续回波裁剪为等效脉冲信号，形成回波矩阵后进行成像处理.

3 基于RVP滤波的信号非线性失真校正

实际工程中，SAL发射的LFM信号线性度往往较差^[2]，本文使用基于RVP滤波的方法进行信号校正^[5-6].

设点目标到雷达的距离为R_i，该目标反射的回波为

$\begin{align} & {{s}_{r}}\left( t \right)=\text{rect}\left( \frac{t-2{{R}_{i}}/C}{{{T}_{p}}} \right)\cdot {{\text{e}}^{\text{j}2\text{ }\!\!\pi\!\!\text{ }\left\{ {{f}_{c}}\left( t-2{{R}_{i}}/C \right)+\frac{1}{2}\gamma {{\left( t-2{{R}_{i}}/C \right)}^{2}} \right\}}}\cdot \\ & {{\text{e}}^{\text{j}2\text{ }\!\!\pi\!\!\text{ }\!\!\varepsilon\!\!\text{ }\left( t-2{{R}_{i}}/C \right)}}, \\ \end{align}$

(3)

其中，t为快时间，T_p为扫频周期，C为光速，f_c为载频，γ为快时间调频率，e^j2πε(t)为发射信号的非线性失真项，通常可通过信号内定标获得^[7-9]，其中，$\varepsilon \left( t \right)=\sum\limits_{n=3}^{N}{{{\alpha }_{n}}{{t}^{n}}}$，含有3阶及以上误差项，本质上，RVP滤波法对非线性失真的阶次没有要求.

以R_ref为参考斜距对该回波去斜，设R_Δ=R_i-R_ref，去斜后的差频输出为

$\begin{align} & {{s}_{if}}\left( t \right)={{s}_{r}}\left( t \right)\cdot s_{\text{ref}}^{*}\left( t \right) \\ & =\text{rect}\left( \frac{t-2{{R}_{i}}/C}{{{T}_{p}}} \right)\cdot {{\text{e}}^{-\text{j}\frac{4\text{ }\!\!\pi\!\!\text{ }}{C}\gamma \left( t-\frac{2{{R}_{\text{ref}}}}{C} \right)R\Delta }}\cdot \\ & {{\text{e}}^{-\text{j}\frac{4\text{ }\!\!\pi\!\!\text{ }}{C}{{f}_{c}}R\Delta }}\cdot {{\text{e}}^{\text{j}\frac{4\text{ }\!\!\pi\!\!\text{ }}{{{C}^{2}}}R_{\Delta }^{2}}}\cdot {{\text{e}}^{j2\text{ }\!\!\pi\!\!\text{ }\varepsilon \left( t-2{{R}_{i}}/C \right)}}. \\ \end{align}$

(4)

将该差频信号沿快时间傅里叶变换(以参考点的时间为基准)

$\begin{align} & {{S}_{if}}\left( f \right)=\left\{ {{T}_{p}}\sin c\left[ {{T}_{p}}\left( f+2\frac{\gamma }{C}R\Delta \right) \right]\cdot \right. \\ & \left. {{\text{e}}^{-\text{j}\left( \frac{4\text{ }\!\!\pi\!\!\text{ }fc}{C}R\Delta +\frac{4\text{ }\!\!\pi\!\!\text{ }\gamma }{{{C}^{2}}}R_{\Delta }^{2}+\frac{4\text{ }\!\!\pi\!\!\text{ }f}{C}R\Delta \right)}} \right\}\otimes FT\left\{ {{\text{e}}^{\text{j2 }\!\!\pi\!\!\text{ }\varepsilon \left( t-\frac{2R\Delta }{C} \right)}} \right\}, \\ \end{align}$

(5)

上式卷积号前的相位项中，第2项是RVP项，第3项是包络斜置项，均应予以去除^[10].这2项都与R_Δ有关，对不同的R_Δ应作出不同的相位补偿.但是从公式看，差频信号变到频域后成为宽度很窄的sinc函数，也就是说，对斜距R_Δ的目标进行补偿时，只需要补偿$f=-2\frac{\gamma }{C}R\Delta $处的相位即可.基于上述考虑，式(5)可化简为

$\begin{align} & {{S}_{if}}\left( f \right)={{T}_{p}}\cdot {{\varphi }_{\varepsilon }}\left( f+2\frac{\gamma }{C}R\Delta \right)\cdot \\ & {{\text{e}}^{\text{j}\frac{\text{ }\!\!\pi\!\!\text{ }}{\gamma }{{f}^{2}}}}\cdot {{\text{e}}^{\text{-j}\frac{\text{4 }\!\!\pi\!\!\text{ }{{f}_{c}}}{C}R\Delta }}, \\ \end{align}$

(6)

其中，φ_ε(f)=FT{e^j2πε(t)}，对式(6)乘以S_c(f)=${{\text{e}}^{\text{-j}\frac{\text{ }\!\!\pi\!\!\text{ }{{f}^{2}}}{\gamma }}}$即可将RVP项和包络斜置项去除，再逆傅里叶变换到时域

${{S}_{if}}\left( t \right)={{T}_{p}}\cdot {{\text{e}}^{\text{j2 }\!\!\pi\!\!\text{ }\varepsilon \left( t \right)}}\cdot {{\text{e}}^{\text{-j}\frac{\text{4 }\!\!\pi\!\!\text{ }{{f}_{c}}}{C}R\Delta }}\cdot {{\text{e}}^{\text{-j2 }\!\!\pi\!\!\text{ }\frac{2\gamma R\Delta }{C}t}}.$

(7)

可以看出，去除RVP项和包络斜置项后，信号非线性失真和目标斜距不再相关，可以用e^－j2πε(t)统一补偿.将补偿后的信号再变到频域即可取得理想的脉压效果

${{s}_{if}}\left( t \right)={{T}_{p}}\cdot \sin c\left( f+\frac{2\gamma {{R}_{\Delta }}}{C} \right)\cdot {{\text{e}}^{\text{-j}\frac{4\text{ }\!\!\pi\!\!\text{ }{{f}_{c}}}{C}{{R}_{\Delta }}}}.$

(8)

4 信号采样和成像处理仿真

信号采样和成像处理流程为：参考由GPS数据换算出的延时及最大延时误差，根据第3节给出的原则，选取一段合适的回波去斜脉压以进行延时估计(这其中也需非线性失真的校正)；根据延时估计结果，将连续采集的回波裁剪成等效脉冲信号并形成回波矩阵，去斜脉压后对信号进行非线性失真校正并方位成像.

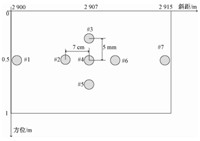
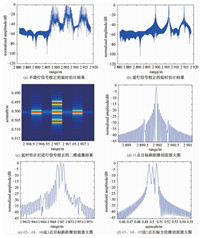
表 2给出本文的仿真参数，点目标位置及编号如图 3所示，场景中心的5个点目标斜距间隔7 cm，方位间隔5 mm.对比图 4(a)和图 4(b)，RVP滤波法对信号进行了有效的非线性失真校正.校正后，延时估计精度有所提高；图 4(c)是场景中心的成像结果，可以看出5个点目标得到了清楚分辨；图 4(d)给出斜距最近的#1点目标的斜距维切面放大图(斜距最远的#7点目标与之基本相同，不再给出)；图 4(e)给出#2、#4、#6这3点目标的斜距维切面放大图；图 4(f)给出#2、#4、#6这3点目标的方位切面放大图；可以看出，数字去斜并进行非线性失真校正后，脉冲压缩的主副瓣分布情况和高速采样下LFM信号脉压情况基本一致，斜距向和方位向均达到了预期分辨率.低采样率数字去斜应用于SAL的可行性得到验证.

5 结束语

本文将低采样率数字去斜技术应用于SAL；分析系统的快时间采样率；给出成像处理流程.仿真验证了低采样率数字去斜应用于SAL的可行性.在本文参数下，对带宽4 GHz，线性度1/1 000的信号，快时间采样率设置为100 MHz即可满足要求，大幅度降低了SAL系统的数据量；若将快时间采样率设置为200 MHz，可使用单路AD实施采样，进一步简化系统.本文的研究工作对SAL的工程研制具有一定的参考价值.