2. 中国科学院光电研究院, 北京 100094
2. Academy of Opto-Electronics, Chinese Academy of Sciences, Beijing 100094, China
傅里叶叠层成像是一种能够利用多角度光照明和低数值孔径的物镜重建出具有高分辨率图像的相位恢复技术[1].与传统的叠层成像技术相似,傅里叶叠层成像利用在频域上形成光谱的叠层恢复出样本的复振幅分布,因此也具有收敛速度快和消除解的二义性等优点[2-4].然而,傅里叶叠层成像并不是用扫描相干衍射的方法,而是采用合成孔径的概念[5-6].与传统叠层成像相比,傅里叶叠层成像的受限支撑不是受限的照明光束,而是傅里叶域受限的光学传递函数[7-12].除此之外,傅里叶叠层成像系统中由于引入了低数值孔径的透镜,不仅可以扩大视场,提高信噪比和分辨率,而且能降低对光源相干性的要求.并且,傅里叶叠层成像还可以突破物镜本身的限制,在消除透镜带来的像差的同时增加景深[11].
光学信息安全技术由于其具有高设计自由度、多加密维度、高鲁棒性、高速并行处理的能力和难以破解等诸多优势,而受到诸多研究学者的关注[13].自从Refregier和Javidi[14]提出基于双随机相位的加密方法以来,光学图像加密便成为一个研究热点.在此方面,近年来不断有新的进展. Liu等[15]提出一种基于级联分数傅里叶变换的光学图像加密系统,具有良好的安全性;Situ和Zhang[16]将波长复用技术引入到菲涅尔域的双随机相位加密系统中,完成了多幅图像的加密;Shi等[17]提出一种基于叠层成像的光学图像加密方法,该方法采用的装置简单、适用性强,还能有效地扩大密钥空间以提高系统的安全性.众所周知,图像解密的过程和成像系统中图像恢复的过程相似,鉴于傅里叶叠层成像具有诸多优良性能,于是本文提出一种基于傅里叶叠层成像的光学图像加密技术.该技术是将探针放置在傅里叶频谱面上,采用LED阵列进行多角度的平行光源照明,在频域上形成频谱的叠层,“层”与“层”的交叠扩展了频域带宽.模拟仿真结果表明,该技术既保证了加密系统具有较高的安全性,鲁棒性和解密质量,又能简化装置,提高收敛速度.
1 光学图像加密及解密算法 1.1 加密算法本文提出的基于傅里叶叠层成像的光学图像加密算法是基于传统4f双随机相位编码系统来实现的,如图 1所示.与基于叠层成像的双随机相位光学图像加密系统不同的是,探针紧贴着随机相位板被放在第1个透镜的傅里叶频谱面上,这样就避免了照明光源的机械扫描装置.由于傅里叶叠层成像的关键也在于叠层,频谱的某一“层”,也就是频谱受探针限制通过的某一部分,需要与其他“层”发生交叠,因此重构的每“层”频谱也同时满足其他“层”的频谱约束,最后重构的频谱是所有层的共解,因而提高了迭代速度,增加了重构的准确性.

|
Download:
|
|
图 1 基于傅里叶叠层成像的光学图像加密系统示意图 Fig. 1 Schematic of optical image encryption based on Fourier ptychography |
|
构建如图 2所示的4个不同孔径的探针K1为例.其中黑色为完全遮挡光波的部分,白色为完全透过光波的部分.对于本文所采用的4个不同的探针,使用一个0-1分布的光瞳函数Pi来表征,其定义为

|
Download:
|
|
(a)振幅;(b)相位;(c)随机相位板;(d)密文. K1,K2,K3为模拟所采用的各种不同的探针,其中(e)为P1;(f)为P2;(g)为P3;(h)为P4. 图 2 模拟实验数据 Fig. 2 Data used in simulation |
|
| ${P_i} = \left\{ \begin{array}{l} 1\;通光孔径内\\ 0\;通光孔径外 \end{array} \right.\left( {i = 1,2,3,4} \right),$ | (1) |
其中,下标i表示第i个探针.
加密时,输入的明文f0(x, y)在空域受到随机相位M1: N(x, y)=exp[jn(x, y)]的调制,在频域先后受到探针: Pi和随机相位M2: K(α, β)=exp[jk(α, β)]的滤波,n(x, y)和k(α, β)分别表示2个均匀分布于[0, 2π]的独立随机白噪声序列.加密结果表示如下
| ${\psi _i}{\left| \begin{array}{l} FT\left\{ {FT\left[ {{f_0}\left( {x,y} \right) \cdot N\left( {x,y} \right) \cdot } \right]} \right.\\ \left. {{P_i} \cdot K\left( {\alpha ,\beta } \right)} \right\} \end{array} \right|^2},$ | (2) |
其中,ψi为相应的衍射图样强度,即为所要加密图像对应的密文. FT表示傅里叶变换.
1.2 解密算法由密文和正确的相位密钥,即可采用解密算法恢复出明文信息.从数学的角度来看,该解密算法可以视为傅里叶叠层成像迭代算法的一种特殊形式,并且与传统的叠层成像迭代算法相似.下面简述解密算法:
1)首先估计输入图像的复振幅为fg(x, y),然后开始进行迭代.
2)假设进行到第m次迭代时,对于第i个探针,由前面迭代得出的图像复振幅为figm(x, y).则基于前面加密算法的推导,可得到频谱面上的场分布为
| $f_{ig}^m\left( {\alpha ,\beta } \right) = FT\left[ {f_{ig}^m\left( {x,y} \right) \cdot N\left( {x,y} \right)} \right].$ | (3) |
3)最终输出面上的衍射图样复振幅为
| $D_{ig}^m = FT\left[ {f_{ig}^m\left( {\alpha ,\beta } \right) \cdot {P_i} \cdot K\left( {\alpha ,\beta } \right)} \right].$ | (4) |
4)用记录的强度图样的平方根值
| $D_{ig}^m = {\left( {{\psi _i}} \right)^{\frac{1}{2}}}\frac{{D_{ig}^m}}{{\left| {D_{ig}^m} \right|}}.$ | (5) |
5)原来频谱面场分布对应于通光孔径Pi的部分用新的频谱场分布相应部分替换,得到
| $\begin{array}{l} f_{igs}^m\left( {\alpha ,\beta } \right) = f_{ig}^m\left( {\alpha ,\beta } \right) \cdot \left( {1 - {P_i}} \right) + \\ \;\;\;\;\;\;\;\;\;F{T^{ - 1}}\left( {D_i^m} \right) \cdot {K^*}\left( {\alpha ,\beta } \right) \cdot {P_i}, \end{array}$ | (6) |
其中,
6)继续做傅里叶逆变换,最后再乘M1的复共轭:
| $f_{igN}^m\left( {x,y} \right) = F{T^{ - 1}}\left[ {f_{igs}^m\left( {\alpha ,\beta } \right)} \right] \cdot {N^*}\left( {x,y} \right).$ | (7) |
7)用
8)计算解密图像和密文的相关系数Co.Co是评价2个函数相似程度的量化指标,取值范围为[0, 1],Co值越接近于1,表明2个函数的分布形式越相近. Co的表达式为
| $Co = {\mathop{\rm cov}} \left( {f,{f_0}} \right){\left( {{\sigma _f} \cdot {\sigma _{{f_0}}}} \right)^{ - 1}}.$ | (8) |
其中,f和f0分别为解密图像和原始被加密图像的复振幅,cov(f, f0)为f和f0的互协方差,σf和σf0为标准差.评价解密质量时,需要分别计算振幅和相位的相关系数值CoA和Coφ.
9)如果Co达到预期标准,则此时恢复的复振幅即为所期望得到的解密图像;如果Co未达到预期标准,则将此恢复的复振幅作为初始值,进行下一轮迭代,即对所有的Pi重新进行从步骤2)到8)的计算.进行多次迭代,直至解密出来的图像达到要求.
2 模拟实验与分析我们进行了一系列的模拟实验来验证本文所提出技术的可行性和有效性.分别采用均为256像素×256像素的“Lena”和“Baboon”作为样品的振幅和相位信息,如图 2(a)和图 2(b)所示.选取的2块随机相位板M1和M2均匀独立随机分布在[0, 2π]内,其中一块如图 2(c)所示. 图 2(d)为4个探针中的1个所对应的衍射图样(密文).模拟所采用的探针如图 2中K1,K2,K3所示,其中图 2(f)、2(g)和2(h)可以看做是由图 2(e)分别旋转90°, 180°, 270°得到的.模拟所用的处理器为Intel i7-4790 @ 3.60 GHz,软件为MATLAB R2014a,采用探针K1模拟重建迭代50次所需时间约为1.85 s,迭代30次所需时间约为0.94 s.
2.1 可行性分析通过采用探针K1进行模拟,恢复出来的振幅和相位如图 3(a)和图 3(d)所示,在迭代25次时,得到的振幅和相位相关系数Co均可达到0.999.也就是说,在理想状态下,密文可以快速且无损地解密出来.此外,为了验证本文所提方案的适用性,采用如图 2中K2和K3所示的另外2种不同形状的振幅型探针进行加密和解密,其相应的解密结果如图 3(b)、3(e)和图 3(c)、3(f)所示.由计算结果可知,采用K2可以得到和采用K1相同的良好效果.对于采用K3,在迭代35次之后,得到的振幅Co可达到0.93,相位Co可达到0.97.由此可见,本文提出的加密方案具有很强的可行性.

|
Download:
|
|
(a)和(d) K1;(b)和(e) K2;(c)和(f) K3. 图 3 不同探针对应的解密结果 Fig. 3 Decrypted results with different probes |
|
为了验证探针也可以作为密钥,于是采用正确的随机相位板和错误的探针来进行模拟实验. 图 4为模拟实验解密出来的振幅和相位,其中图 4(a)和4(b)为在解密时将相应加密时采用的探针K1的顺序置乱而解密出来的图像,图 4(c)和4(d)为采用和加密过程不同的探针解密出来的图像.模拟结果表明,使用错误的探针不能解密出预期的图像.也就是说,探针也可作为一种新的密钥,这进一步提高了加密系统的安全性.

|
Download:
|
|
(a),(b)为将探针K1的顺序置乱解密出来的振幅和相位;(c),(d)为采用和加密过程不同的探针解密出来的振幅和相位. 图 4 错误探针对应的解密结果 Fig. 4 Decrypted images with wrong probes |
|
为验证本文加密技术的鲁棒性,分别对密文进行加噪声和剪切操作.模拟采用的均为振幅型探针.模拟结果表明该技术具有很强的抵抗加噪声和剪切攻击的能力.
2.3.1 抗噪声能力分析首先分析本算法对抗各类噪声的有效性.我们分别模拟乘性噪声、椒盐噪声和高斯噪声对解密质量的影响.
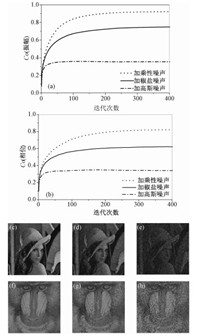
模拟采用的高斯噪声的均值为0,方差为0.01,椒盐噪声和乘性噪声的密度均为0.01. 图 5(a)和5(b)分别是解密之后的图像和原图像之间关于振幅和相位的相关系数Co随迭代次数的变化曲线.由图 5(c),5(f)和5(d),5(g)可以看出本算法能够很好地抵抗乘性噪声和椒盐噪声.相对而言,本算法对于高斯噪声的抵抗能力较差,但是对密文添加了上述高斯噪声后,仍能恢复出具有一定识别度的图像.这些结果表明,本文提出的加密技术能够抵抗一定的噪声攻击.
|
Download:
|
|
(a)振幅相关系数Co;(b)相位相关系数Co;(c)和(f)对应于添加乘性噪声;(d)和(g)对应于添加椒盐噪声;(e)和(h)对应于添加高斯噪声. 图 5 添加不同噪声情况下解密出来的振幅和相位分布及其相应的Co值随迭代次数的变化 Fig. 5 Decrypted results under the attacks of divers noises |
|
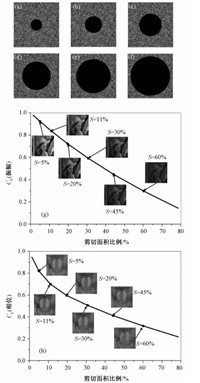
为增加密文被攻击的随机性,分别从密文中心截去占密文5%、11%、20%、30%、45%和60%的圆形部分,如图 6(a)—图 6(f)所示.相应的解密出来的结果如图 6(g)和6(h)所示.此外,图 6(g) 和6(h)还分别示出了在迭代30次左右时振幅和相位Co值随剪切面积的变化曲线.由图 6(g)和6(h)可以直观地看出当密文被剪切30%时,振幅和相位Co值都能达到0.5以上,具有较高的解密质量;当密文被剪切大约60%时,解密出来的振幅和相位仍具有一定的可辨识度.由此可见,本文所提出的方法具有很强的抗剪切攻击能力.
|
Download:
|
|
(a) 5%;(b) 11%;(c) 20%;(d) 30%;(e) 45%;(f) 60%;(g)振幅分布情况;(h)相位分布情况. 图 6 不同剪切面积的密文以及相应的重建图像的Co值 Fig. 6 Ciphertexts at different occlusion percentages and relationship between values of Co and occlusion percentages |
|
本文将傅里叶叠层成像用于双随机相位光学图像加密系统.一方面,置于傅里叶频谱面上的滤波孔径可以作为新的密钥,显著增大了系统的密钥空间.另一方面,该技术采用平行光多角度照明,降低了对光源相干性的要求,能够简化实验装置.模拟结果表明,该技术的收敛速度快,并且具有较强的可行性和较高的鲁棒性.此外,该技术还可以用来对三维图像进行加密和隐藏,具有广阔的应用前景.
| [1] | Zheng G, Horstmeyer R, Yang C. Wide-field, high-resolution Fourier ptychographic microscopy[J]. Nat Photonics , 2013, 7 (9) :739–745. DOI:10.1038/nphoton.2013.187 |
| [2] | Ou X, Horstmeyer R, Yang C, et al. Quantitative phase imaging via Fourier ptychographic microscopy[J]. Opt Lett , 2013, 38 (22) :4845–4848. DOI:10.1364/OL.38.004845 |
| [3] | Faulkner H M L, Rodenburg J M. Movable aperture lensless transmission microscopy:A novel phase retrieval algorithm[J]. Phys Rev Lett , 2004, 93 (2) :023903. DOI:10.1103/PhysRevLett.93.023903 |
| [4] | Zheng G, Ou X, Horstmeyer R, et al. Fourier ptychographic microscopy:a gigapixel superscope for biomedicine[J]. Opt Photon News , 2014, 25 (4) :26–33. DOI:10.1364/OPN.25.4.000026 |
| [5] | Garc1'a J, Zalevsky Z, Fixler D. Synthetic aperture superresolution by speckle pattern projection[J]. Opt Exp , 2005, 13 (16) :6073–6078. DOI:10.1364/OPEX.13.006073 |
| [6] | Alexandrov S A, Hillman T R, Gutzler T, et al. Synthetic aperture Fourier holographic optical microscopy[J]. Phys Rev Lett , 2006, 97 (16) :168102. DOI:10.1103/PhysRevLett.97.168102 |
| [7] | Guizar-Sicairos M, Fienup J R. Phase retrieval with transverse translation diversity:a nonlinear optimization approach[J]. Opt Exp , 2008, 16 (10) :7264–7278. DOI:10.1364/OE.16.007264 |
| [8] | Hoppe W, Strube G. Diffraction in inhomogeneous primary wave fields. 2. Optical experiments for phase determination of lattice interferences[J]. Acta Crystallogr , 1969, A 25 :502–507. |
| [9] | Shi Y S, Wang Y L, Zhang S G. Generalized ptychography with diverse probes[J]. Chin Phys Lett , 2013, 30 (5) :054203. DOI:10.1088/0256-307X/30/5/054203 |
| [10] | Dong S, Shiradkar R, Nanda P, et al. Spectral multiplexing and coherent-state decomposition in Fourier ptychographic imaging[J]. Biomed Opt Express , 2014, 5 (6) :1757–1767. DOI:10.1364/BOE.5.001757 |
| [11] | Zheng G. Fourier ptychographic imaging[J]. IEEE Photonics Journal , 2014, 6 (2) :0701207. |
| [12] | Horstmeyer R, Yang C. A phase space model of Fourier ptychographic microscopy[J]. Opt Exp , 2014, 22 (1) :338–358. DOI:10.1364/OE.22.000338 |
| [13] | Javidi B. Securing information with optical technologies[J]. Physics Today , 1997, 50 (3) :27–32. DOI:10.1063/1.881691 |
| [14] | Refregier P, Javidi B. Optical image encryption based on input plane and Fourier plane random encoding[J]. Opt Lett , 1995, 20 (7) :767–769. DOI:10.1364/OL.20.000767 |
| [15] | Liu S, Yu L, Zhu B. Optical image encryption by cascaded fractional Fourier transforms with random phase filtering[J]. Opt Commun , 2001, 187 (1) :57–63. |
| [16] | Situ G H, Zhang J J. Multiple-image encryption based on wavelength multiplexing[J]. Opt Lett , 2005, 30 (11) :1306–1308. DOI:10.1364/OL.30.001306 |
| [17] | Shi Y S, Li T, Wang Y L, et al. Optical image encryption via ptychography[J]. Opt Lett , 2013, 38 (9) :1425–1427. DOI:10.1364/OL.38.001425 |
 2016, Vol. 33
2016, Vol. 33 


