地球重力场模型是地球引力位的球谐函数表达，表现为一组截断到有限阶次的球谐函数级数展开式的系数，用于确定地球的物理形状及其外部重力场，可以说地球重力场模型是物理大地测量研究成果的集中体现^[1].自20世纪50年代，Kaula首次构建世界上第一个8阶次地球重力场模型以来，迄今为止全世界构建并公开发布的地球重力场模型已逾150个.随着大地测量观测技术的进步，地球重力场信号种类更加丰富、质量也不断提高，因此，地球重力场模型精度和分辨率较以往得到较大的改善.特别是本世纪以来，以CHAMP、GRACE和GOCE卫星重力计划的实施为代表，突破了传统方法获取重力场信息的局限，使得物理大地测量的研究从局部扩展至全球，从静态发展到动态，将地球重力场模型的构建带入一个崭新时代，模型的阶次也从20世纪末的全阶次360，迅速发展到现在的全阶次2 159(部分阶扩展到2 190)，其大地水准面精度也从几米提高到几十厘米、几厘米乃至几个毫米(长波频段).

地球重力场模型的精度评价是模型构建和应用的重要内容.常用精度评价方法包括模型位系数阶方差e_n，以及利用模型解算得到重力场元与实测值的比较，如重力异常、高程异常、垂线偏差等^[2].模型位系数阶方差${{e}_{n}}=\sqrt{\frac{1}{2n+1}\sum\limits_{i=1}^{n}{\left[ {{({{\sigma }_{{{C}_{nm}}}})}^{2}}+{{({{\sigma }_{{{S}_{nm}}}})}^{2}} \right]}}$评价，其中σ_Cnm和σ_Snm分别为相应阶次模型位系数的中误差，该方法需要准确可靠的位系数中误差，在模型解算时须构建观测量与模型位系数之间准确的协方差函数，并利用最小二乘法进行模型解算.融合多源重力场观测数据恢复高阶地球重力场模型时，存在协方差构建和超高价法方程解算的困难，致使解算得到的模型位系数中误差的准确性和可靠性无法保证^[3].在实际的应用中，σ_Cnm和σ_Snm也常用解算模型与参考模型的位系数之差代替，用于表示解算模型与参考模型之间的差异.重力异常误差${{\sigma }_{\Delta g}}=\sqrt{\frac{1}{n-1}\sum\limits_{i=1}^{n}{{{(\Delta g_{\text{EGM}}^{i}-\Delta g_{\text{REAL}}^{i})}^{2}}}}$评价方法、高程异常误差${{\sigma }_{\zeta }}=\sqrt{\frac{1}{n-1}\sum\limits_{i=1}^{n}{{{\left( \zeta _{\text{EGM}}^{i}-\zeta _{\text{REAL}}^{i} \right)}^{2}}}}$评价方法，其中Δg_EGMⁱ、ζ_EGMⁱ分别为检验区域计算点模型重力异常和模型高程异常，Δg_REALⁱ、ζ_REALⁱ为相应点的实测重力场元值，n为检验区域的总点数^[4].由于地球重力场模型构建时，其位系数是对大地水准面平均格网重力异常的全球积分，因此利用模型解算得到的计算点重力异常理论上为该点所在区域相应格网的平均重力异常，与该点的实测重力异常存在代表性误差.此外，鉴于引力位的球谐函数表达与Stokes积分公式的等价性，模型地面点高程异常的确切物理意义是过该点处等位面的“当地”水准面差距，即Molodensky意义下的高程异常零阶项，而非实测的具有全频谱特性的高程异常.因此重力异常误差、高程异常误差的评价方法都存在理论上的不严密性.无论是利用何种观测数据和构建方法恢复得到的地球重力场模型，其静态重力场模型都是对实际地球质体真实重力场的逼近表达，理论上表示的是同一个真值.不同地球重力场模型的分辨率和精度迥异，虽然利用纯卫星重力观测数据恢复得到中低阶(一般低于200阶)模型，在上千千米的尺度上表达大地水准面起伏可达到亚厘米级精度，因为该尺度平滑了地球重力场的高频部分，致使其精度指标仅在较大尺度上有意义.当前，对于高阶地球重力场模型的精度评价依然是个难题.

Gauss-Listing于19世纪给出的大地水准面经典定义是与平均海水面最佳拟合的重力等位面^[5].实践证明该经典定义在实际应用中存在两方面的缺陷，一是由于海流和海洋潮汐的存在难以得到排除所有动力学影响的平均海平面；二是严格意义上平均海水面并不是重力等位面^[6].因此，随后提出“理想的海洋面”、“无干扰的平均海面”，以及“海面地形平均值为零”等定义，旨在克服经典大地水准面定义的理论缺陷.基于广义相对论原理，Bejerhammar^[7]、申文斌等^[8]提出等时率和等频相对论大地水准面，更加吻合大地水准面的等位面特性，但在实现上存在困难.晁定波等^[9]基于大地水准面的理论特性，提出一个理论严密且可实现的全球大地水准面定义，即大地水准面是一个与纳入到统一潮汐系统的某一历元全球平均海面最佳拟合的重力等位面，所谓最佳拟合是指大地水准面上的位常数W₀等于一个格网化全球平均海面模型所有格网中心点重力位值的均值，并在全球保持位常数不变，全球平均海平面的重力位值由一个具有相应分辨率的全球重力位模型确定.该定义不仅符合大地水准面的理论特性，明确了大地水准面与地球重力场模型的关系，且具有可唯一实现性^[10].

本文根据大地水准面特性，提出一种基于Gauss-Listing大地水准面经典定义的地球重力场模型评价方法，并给出重力位离散度作为评价指标.首先介绍地球重力场模型常用评价方法及其存在的问题，随后给出基于经典大地水准面定义的地球重力场模型评价方法的基本思想和实现关键，接着利用3个不同的参考大地水准面对实际模型精度进行评价，最后就本文方法的应用效果与结论进行讨论.

1 基于大地水准面经典定义的重力场模型评价

从确定地球物理形状即大地水准面的角度而言，地球重力场模型就是综合利用重力场多源观测数据构建一个从理论上逼近大地水准面经典定义的重力等位面.不同地球重力场模型所采用的数据和构建方法存在差异，致使其确定的地球重力场模型对实际地球重力场表达能力有所不同，但在不考虑时变因素和参考椭球差异时，其本质上都是对同一个真实地球重力场的理论逼近.

根据晁定波等提出的全球大地水准面定义的最佳拟合原则^[9]可知，大地水准面上的位常数W₀等于全球平均海面模型上重力位值的均值，该全球平均海面的重力位值源于某一全球重力位模型.由Gauss-Listing大地水准面经典定义可知，作为重力位等位面的大地水准面上的重力位应为恒定值，其离散度理论上为零，实际上的非零反映着地球重力场模型的理论表达能力.由于地球重力场模型误差的客观存在，格网化全球平均海面模型所有格网中心点重力位值W_i与其均值即大地水准面位常数W₀必然存在一定的偏差，其离散度反映着大地水准面与平均海面模型之间的拟合程度，即离散度越小说明地球重力场模型理论符合度越优.因此，本文基于Gauss-Listing大地水准面经典定义和晁定波等提出的全球大地水准面定义，提出利用大地水准面上重力位离散度作为地球重力场模型精度优劣的评价方法.具体表述为：选取某局部或全球大地水准面，作为重力等位面的参考面，以格网点形式表达，利用地球重力场模型计算该参考面上对应格网点的重力位W_ij，其平均重力位值为$\bar{W}=\frac{1}{i\times j}\sum{\sum{{{W}_{ij}}}}$，进而计算该参考面上的重力位离散度δ_W如式(1)所示，以此作为地球重力场模型精度的评价指标，即重力位离散度越大说明该地球重力场模型理论精度越差，反之则越优.该指标既可用于不同地球重力场模型间的优劣比较，又可评价同一地球重力场在全球不同区域的表达能力.

${{\delta }_{W}}=\pm \sqrt{\frac{1}{i\times j-1}\sum{\sum{{{({{W}_{ij}}-\bar{W})}^{2}}}}}.$

(1)

该方法的实现关键是作为参考面的重力等位面的选取问题，一方面希望该参考面具有较高的精度，否则重力位离散度更多表现为该参考面的误差；另一方面希望该参考面独立于被评价的地球重力场模型，否则重力位离散度不具有独立意义.但是在实际应用中，该参考面仅作为“尺子”来评价地球重力场模型，特别用于衡量与该参考面独立的地球重力场模型具有可行性，诚然其精度越高、独立性越强对地球重力场模型理论表达能力评价的准确性越高、可靠性越强.为进一步验证本文方法的可行性与可靠性，下面分别选取平均海平面、陆地大地水准面以及全球大地水准面作为参考面，对常见的多个地球重力场模型的精度进行比较和评价.

2 算例分析

本文研究涉及的地球重力场模型包括OSU91A、EGM96、ITG-Grace03、EGM2008^[11]、EIGEN-6C4、GOCO05S^[12]等，各模型的基本情况及其参考椭球信息详见表 1和表 2.

其中，OSU91A是综合利用当时卫星测高数据和地面重力测量数据以及地形信息组合构建的完全到360阶次地球重力场模型，并利用中国大约1 000个地面重力观测数据，其多源数据融合构建地球重力场模型的方法为后续模型的构建奠定了基础.EGM96是综合利用更为丰富和更长时序的多源重力数据构建的完全到360阶地球重力场模型，其中增加了SPOT2卫星的DORIS跟踪数据，该地面信标网全球覆盖，对模型构建贡献较大，同时利用T/P、ERS1和GEOSAT/ERM卫星测高数据确定了20阶次的大洋动力地形球谐模型，在卫星测高数据处理时扣除大洋动力地形影响后推算30′×30′的海面平均重力异常，提供了更加精准的海面重力异常用于模型构建，使得EGM96的精度要全面优于OSU91.ITG-Grace03是利用2002年12月至2007年4月间的GRACE卫星观测数据，未使用任何其他数据、先验信息，且未采用任何正则化方法，利用短弧积分法构建的完全到180阶的静态重力场模型.EGM2008综合利用地面重力、卫星测高和卫星跟踪以及卫星重力观测数据构建的完全阶次到2 160，最高阶数扩展到2 190，在卫星重力数据利用方面，仅利用了GRACE数据，该模型的地面分辨率半波长约为9 km、全波段大地水准面精度约为十几个厘米^[13].EIGEN-6C4综合利用当时可以利用的多源重力场信息构建的完全阶次到2 190阶的地球重力场模型，相比于EGM2008而言根本区别在于增加了2009年11月1日至2013年10月20日期间的GOCE卫星重力梯度观测数据，对模型的贡献至235阶，理论阶方差显示其精度要优于EGM2008，利用GPS水准检核表明其大地水准面精度与EGM2008相当^[14].GOCO05S是综合利用GRACE、GOCE、SLR纯卫星观测数据构建的全阶次到280的地球重力场模型，阶方差显示在前280阶要优于EGM2008地球重力场模型.各模型的大地水准面阶次误差如图 1所示，其中高阶模型仅显示到360阶.

2.1 基于区域海洋大地水准面的模型分析

平均海平面是大地水准面定义和实现的渊源.随着卫星测高技术的应用，利用卫星测高获取的海面高，扣除海面地形影响可得海洋大地水准面，且该海平面独立于地球重力场模型.本文首先选取太平洋某区域卫星测高获得的平均海平面作为全球重力等位面的代表区域，用于地球重力场模型优劣评价.选取的平均海平面区域范围为N15°~N20°、E150°~E155°，分辨率为1′×1′，共计90 000个点，该区域的平均海面大地高最小为28.855 0 m、最大为46.631 0 m，平均为38.035 6 m，对应的地球参考椭球长半轴为6 378 136.3 m、扁率为1/298.275，该模型为实测海面大地高扣除海潮等影响后得到平均的静止海平面，并进行海面地形影响改正后可视为海洋大地水准面，有关情况见图 2.

因不同地球重力场模型所采用的参考椭球不同，地球重力场模型采用的参考椭球参数与所选取的平均海平面模型采用的参考椭球参数亦不同，在实际计算中，须进行参考椭球基准统一.因地球重力场模型位系数无法直接进行转换，只能将平均海平面格网点转换到地球重力场模型相对应的参考椭球.具体转换方法为：1)将平均海平面模型计算点(B、L、H)由其对应的参考椭球转换到地球重力场模型对应的参考椭球下得到新的计算点(B′、L′、H′)；2)利用地球重力场模型计算新的计算点(B′、L′、H′)在地球重力场对应地球参考椭球下的重力位值及平均重力位值；3)利用式(1)可得该地球重力场模型在平均海平面上的重力位离散度^[15].针对不同地球重力场模型利用上述步骤1)至3)即可得到不同地球重力场模型在该区域平均海平面上的重力位离散度，计算结果见表 3和表 4.

其中表 3为未剔除粗差的不同地球重力场模型在该平均海平面上的重力位值及其离散度，表 4为剔除粗差后的统计结果.可见，在该参考面区域，地球重力场模型OSU91A、EGM96的重力位离散度分别为±5.123 5 m²·s^-2和±3.290 4 m²·s^-2，说明EGM96的精度要优于OSU91；地球重力场模型EGM08、EIGEN-6C4的重力位离散度分别为±3.165 1 m²·s^-2和±3.167 1 m²·s^-2，说明这2个模型的精度相当且优于其他模型，地球重力场模型ITG-Grace03、GOCO05S的重力位离散度分别为±9.688 4 m²·s^-2和±5.073 0 m²·s^-2，说明这2个模型的精度相对较差，这与该2个模型的阶次较低、对实际地球重力场的精细结构表达能力有限有关.此外，通过地球重力场模型EGM2008和GOCO05S的重力位离散度相比可知，虽然阶方差显示在低阶部分GOCO05S要优于EGM2008，但是对于实际地球重力场的表达能力而言EGM2008要优于GOCO05S，说明了地球重力场模型精度与分辨率的辩证关系.

2.2 基于区域陆地大地水准面的模型分析

为进一步验证本文方法，选取陆地上某区域高精度重力大地水准面作为参考面.该区域为综合利用EGM2008地球重力场模型、地面重力观测数据、航空重力观测数据以及地形信息综合确定的区域重力大地水准面模型，无任何GPS水准数据参与模型构建，位于N27°~N31°、W81°~W84°，分辨率为30″×30″，共计43 200个点，该区域的大地高最小为-28.622 0 m、最大为-22.985 0 m，平均为-27.048 1 m，参考椭球为GRS80.利用GPS水准进行外部检核，该模型的大地水准面精度达到±0.8 cm，远优于现有的高阶地球重力场模型的大地水准面累计误差，如EGM2008、EIGEN-6C4等，以此作为参考面对地球重力场模型进行评价具有较强的可靠性.有关情况见图 3.

针对不同地球重力场模型利用2.1中有关参考椭球基准的统一和重力位的计算，即可得到不同地球重力场模型在该区域陆地大地水准面上的重力位离散度，计算结果见表 5和表 6.

其中表 5为未剔除粗差的不同地球重力场模型在该区域陆地大地水准面上的重力位值及其离散度，表 6为剔除粗差后的统计结果.通过各模型的重力位离散度计算结果可见，地球重力场模型EGM2008、EIGEN-6C4精度相当且相对较优，地球重力场模型ITG-Grace03精度相对最差.

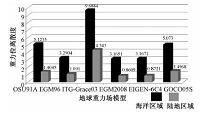
通过比较表 4和表 6的模型重力位离散度，如图 4所示，其中黑色代表区域海洋大地水准面、灰色代表区域陆地大地水准面，计算结果显示对于本文研究的6个地球重力场模型在区域陆地大地水准面的重力位离散度均小于相应的区域海洋大地水准面计算值，说明本文选取的区域陆地大地水准面的精度要高于本文选取的区域海洋大地水准面精度，同时本文研究的6个地球重力场模型在2个参考面上的重力位离散度大小顺序基本一致，仅OSU91A和GOCO05S这2个模型在0.01 m²·s^-2量级上表现相反，总体上验证了本文提出的方法在评价不同地球场模型精度相对优劣评价的可行性.

图 4显示地球重力场模型EGM2008的重力位离散度在0.1～0.01 m²·s^-2量级上小于EIGEN-6C4，这表明地球重力场模型EGM2008要略优于EIGEN-6C4，与图 1中显示的结果不同.

2.3 基于全球大地水准面的模型分析

为进一步验证本文方法的适用性以及EGM2008和EIGEN6C4模型的精度优劣和全球不同区域的精度情况，本文选取美国国家地理空间情报局(NGA)利用地球重力场模型EGM2008直接解算得到的30″×30″分辨率的全球大地水准面作为参考面，该大地水准面参考椭球为WGS84.

由于地球重力场模型构建的数据源无论是种类还是精度或分辨率在全球的分布差异较大，致使同一地球重力场模型在不同区域的表达能力不同.地球重力场模型的构建利用的是全球数据，但其应用却常是局部的，因此地球重力场的全球分布优劣评价既是对地球重力场模型本身优劣评价的需求，也是地球重力场模型应用取舍的重要依据.

为避免代表性误差影响，在利用2.1中有关参考椭球基准的统一和重力位的计算，具体计算点采用与重力场模型分辨率相同的格网点，如EGM2008地球重力场模型完全阶次到2 159，其相应的计算点格网点分辨率为5′×5′，从而得到重力位离散度.计算流程见图 5.

基于上述方法和流程，分别对地球重力场模型EGM2008、EIGEN-6C4进行计算，所得到其全球重力位离散度如表 7所示.

表 7中所述全球重力位离散度是指地球重力场模型在全球某一格网分辨率上的离散度，如EGM2008、EIGEN-6C4所采用的5′×5′的格网分辨率计算得到的全球重力位离散度.根据Gauss-Listing大地水准面经典定义可知，该格网平均重力位值应与全球大地水准面重力位值相等，实际上的差异反映着模型的表达能力和大地水准面的准确度，但每一个格网都是实际地球重力场模型不可或缺的组成部分，因此在离散度的计算中没有采取误差剔除，而是保留了全部格网数值.

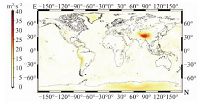
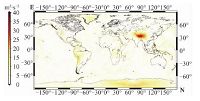
为进一步表达地球重力场模型在全球的表达能力，将全球分为5°×5°的格网，共计36×72个区域，以该模型的5′×5′的格网上的全球重力位值均值为基准，进而得到每个区域相对于全球重力位的离散度，即该模型的区域重力位离散度，其中EGM2008、EIGEN-6C4的全球重力位离散度分布见图 6和图 7.

在5°×5°的全球格网中，地球重力场模型EGM2008的全球重力位离散度最大值位于N30°~35°、E80°~85°区域，其值高达±28.096 0 m²·s^-2；EIGEN-6C4的全球重力位离散度最大值同样位于该区域，其值为±27.753 8 m²·s^-2.通过图 6和图 7以及2个模型的5°×5°的全球重力位离散度的数值计算结果可知，在N30°~35°、E75°~105°范围，2个地球重力场的重力位离散度均较大，基本高于±20 m²·s^-2，远高于该2个模型的全球重力位离散度，说明相对全球而言在该区域2个模型的地球重力场理论符合度均较差，详见表 8.

从图 6、图 7及表 8可见，地球重力场模型EGM2008和EIGEN-6C4无论是大地水准面上的重力位平均值还是全球重力位离散度均相当，说明该2个模型对于实际地球重力场表达的理论符合度相似，且就全球而言，N30°~35°、E80°~85°区域范围，2个模型对于实际重力场的表达均较差，其中EIGEN-6C4稍劣.部分区域的重力位值及其离散度远大于全球的重力位平均值及其离散度，源于异常值的存在，从统计学角度而言，未剔除异常值的统计结果难以准确表达全局特性，因此，对EGM2008、EIGEN-6C4这2个重力场模型的5^′×5^′的格网重力位值按照正态分布规律进行粗差剔除，处理后的全球重力位值统计结果见表 9.

由表 9可见，地球重力场模型EGM2008、EIGEN-6C4的全球重力位均值分别为62 636 855.893 2 m²·s^-2和62 636 855.901 8 m²·s^-2，与国际地球自转与参考系统服务(International Earth Rotation and Reference Systems Service,IERS)IERS2010协议推荐的全球重力位值W₀=(62 636 856.0±0.5) m²·s^-2要求相符.其重力位离散度分别为±1.108 3 m²·s^-2和±1.380 2 m²·s^-2，由扰动位和大地水准面高的关系$N=\frac{T}{\gamma }$可得${{\delta }_{N}}=\frac{{{\delta }_{r}}}{\gamma }$，其中γ为全球平均重力值可取γ=9.80 m·s^-2，EGM2008、EIGEN-6C4对于大地水准面的全球平均理论表达精度分别为±0.113 1 m和±0.140 8 m，计算结果表明在厘米级精度上EGM2008要略优于EIGEN-6C4.

3 结论

本文提出一种基于Gauss-Listing大地水准面经典定义的地球重力场模型优劣评价方法及重力位离散度的评价指标，该方法是一种负向与相对评价方法.鉴于参考大地水准面本身存在误差，无法通过重力位离散度指标简单量化地球重力场模型的绝对精度，但是可以通过不同地球重力场模型在同一参考大地水准面或者同一地球重力场模型在全球不同区域的重力位离散度来判定不同地球重力场模型或同一地球重力场模型不同区域符合度的相对优劣.

本文给出OSU91A、EGM96、ITG-Grace03、COCO05S等具有代表性的全球重力场模型在某大地水准面区域的优劣评价和EGM2008、EIGEN-6C4地球重力场模型在全球的重力位离散度分布及优劣评价，指出方法应用中有关椭球基准统一、格网重力位离散度解算等关键问题，得出EGM2008、EIGEN-6C4这2个地球重力场模型对实际地球重力场表达能力相当的结论，以及该2个模型表达的大地水准面的理论精度约为±11.3 cm和±14.1 cm.同时发现该2个模型在N30°~N35°、E80°~E85°区域范围内，对于实际地球重力场的表达相对全球而言较差.此外，图 1给出的地球重力场模型位系数阶方差显示EIGEN-6C4的精度要略优于EGM2008，但本文研究却得出了相反结论，无论是陆地、海洋还是全球大地水准面作参考面均得到同样结论，验证了本文方法的准确性，也说明EGM2008精度上要略优于EIGEN-6C4.

中国测绘科学研究院的柯宝贵博士、蒋涛博士提供了2.1中的区域海洋大地水准面模型和2.2中的区域陆地大地水准面模型数据，北京市测绘设计研究院的曾艳艳博士对文章提出了建议，在此一并致谢.