为解决和平利用聚变能问题,国际上设立了热核聚变实验堆计划(international thermonuclear experimental reactor,ITER)[1].该计划中,液态双冷锂铅包层(dual coolant lead lithium,DCLL)[2]是一种重要概念,包层中的流道插件(flow channel insert,FCI)是置于金属流体中的一个关键部件[3].
目前很多研究工作中都开展了对包层结构和流道插件的分析,其中包括磁流体、流动传热和结构力学分析等. Wang和Tang[4]基于FLUENT扩展包进行包层结构中磁流体的流动分析,获得其速度分布. Smolentsev等[5]研究压力降对流动带来的影响和包层流道中的传热特性等问题. Vitkovsky等[6]的多场分析中,利用梁和薄壳单元简化模型计算结构部件,边界条件考虑流体压力、重力、热场和电磁力的影响,并采用弹性支撑的条件.Sharafat等[7]分析有泡沫化处理夹层的碳化硅复合材料,利用顺序耦合的方式,首先进行磁流体力学分析,将得到的热场进行插件的结构分析. Sharafat等[8]进行碳化硅插件结构安全性的试验研究,他们采用热辐射以及浸入液态金属两种方式,结合有限元法计算的应力分布,分析流道插件的结构安全性,其中,加热棒加热时流道插件棱边和转角处出现了最大应力,且最大应力十分接近碳化硅材料的设计极限. 另外,在Ying等[9]的多场耦合分析中,同样对于包层中的结构安全性进行分析,得到的最大结构应力已经超过材料极限,说明包层结构的优化设计十分必要.
在包层的工作环境下,流道插件的力学响应是一个多场耦合问题,包括磁场、热场、流场和结构场. 这里,我们利用有限体积、有限元方法,进行包层结构中的磁流体流动传热求解场和流道插件的结构应力、应变求解. 重点关注碳化硅复合材料的物性参数对包层的影响,主要是不同结构热导率的影响,并对一种典型设计中的流道插件进行拉、压应力,厚度、面内应力的详细分析,从而为包层和流道插件的结构安全性和进一步的优化设计提供参考.
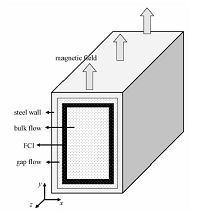
1 计算模型和方法 1.1 计算模型如图 1所示的计算模型是以液态双冷锂铅包层为原型建立的. 表 1列出模型中主要各部分的材料属性. 在图 1中x、y、z分别为径向、环向、极向,与反应堆中常用的坐标系相符合. 流道的横截面为矩形,具有0.06 m/s进口速度的金属流体的流动方向为极向,初始的进口温度取为460 ℃左右,外层左边的钢壁称作第一壁,它是较为危险的部件,面对温度极高的反应堆中心区,它的最高温度应在550 ℃以下,以保障整体结构的安全性. 钢壁的外侧简化为通过氦气进行对流换热的边界条件. 而流道插件是嵌套在流道中的部件,它将流体分隔成通道中心区域的主流区,以及钢壁和插件中间的间隙流区两大部分. 插件的制作材料是具有高热稳定性能的碳化硅复合材料,它的作用是减小金属流体的压力降,以减小驱动的泵功率,同时起到隔热作用,减少热损耗,增加金属流体出口的平均温度,在提高后续换热效率的同时,确保第一壁的安全.
|
Download:
|
| 图 1 典型包层流道结构示意图 Fig. 1 Geometry of DCLL flow channel | |
|
|
表 1 材料属性 Table 1 Material parameters |
外部磁场主要作用在环向,我们将与磁场平行方向的壁面称作侧壁,而磁场垂直穿过的则称为哈特曼壁,钢壁的外边缘尺寸为0.224 m×0.324 m×2 m.
1.2 控制方程受到外加强磁场的金属流体在包层中流动时,应满足以下方程:
动量方程
| $\rho \frac{\partial u}{\partial t}+\rho u\cdot \nabla u=-\nabla p+\Delta \cdot \left( \eta \nabla u \right)+J\times B,$ | (1) |
连续性方程
| $\Delta \cdot u=0,$ | (2) |
电荷守恒:
| $\Delta \cdot J=0,$ | (3) |
电势泊松方程
| $\nabla \cdot ({{\sigma }_{0}}\Delta \phi )=\nabla \cdot ({{\sigma }_{0}}u\times B),$ | (4) |
其中传热满足能量方程
| $\rho {{C}_{p}}\left( \frac{\partial t}{\partial t}+u\cdot \nabla T \right)=\nabla \cdot \left( K\nabla T \right)+\frac{{{J}^{2}}}{{{\sigma }_{0}}}+Q$ | (5) |
这里,ρ,u,p,,J,B,T分别为密度、流体速度、压强、电势、电流、磁场强度和温度.η,σ0,Cp,K分别表示黏性、电导率、定压比热容和热导率.Q表示体积热源,该项是由于锂铅流体在中子辐照下会产生持续的体积热源,其分布形式由中子学计算得到的指数分布形式[10]确定:
| $Q=30\times {{10}^{6}}exp\left[ -10\left( x+a/2 \right) \right].$ | (6) |
这里,a为径向的主流区域宽度,x是原点位于槽道中心的径向坐标.
在固体部分的求解中,由于碳化硅较好的电绝缘性,我们忽略固体中的电磁力影响和焦耳耗散热量.而碳化硅材料在中子辐照下的热生成远小于金属流体,因此不考虑体积热源的影响. 同时在钢壁和外侧的氦气的对流换热中,应该满足如下的换热量
| ${{q}^{*}}={{h}_{f}}({{T}_{S}}-{{T}_{F}}),$ | (7) |
这里,TS和TF分别为固体和流体侧的温度,而hf则表示对流换热系数.
在流道插件的结构分析中,应满足如下方程:静力平衡
| ${{\sigma }_{ij,j}}+{{\overline{f}}_{i}}=0,\text{ }\left( i,j=x,y,z \right),$ | (8) |
几何方程
| ${{\varepsilon }_{ij}}=\frac{1}{2}({{u}_{i,j}}+{{u}_{j,i}})$ | (9) |
本构关系
| ${{\sigma }_{ij}}={{D}_{ijkl}}{{\varepsilon }_{kl}},$ | (10) |
这里,ui、σij、εij表示固体中的位移、应力和应变场,Dijkl和fi为弹性系数矩阵和固体受到的外载荷.
1.3 算法和模型验证对于黏性不可压磁流体力学方程的求解,除满足动量和连续性方程之外,增加了电势泊松方程的求解和需要满足的电荷守恒等条件. 同时,在N-S方程中体力源项为电磁力. 在大哈特曼数的计算中,保证电荷和动量守恒较为困难,本文采用倪明玖等[11-13]的相容守恒格式,计算电流分为两部分,电势梯度项和速度引起的电流项离散格式保持一致,并与电势泊松方程求解的格式一致,同时将电流在网格中心守恒重构,保证电荷守恒,从而可以有效保证考虑了电磁力后的动量守恒.
对于这种相容守恒格式下的有限体积法和有限元法结合的代码,我们在以前的工作中已经提供了系列验证算例[11-13],在大哈特曼数算例下,磁流体部分可以取得较高的计算精度,并通过了精确解和试验的验证. 固体区域的求解中,通过解析解验证和网格无关性验证,同样保证了计算的精度. 限于篇幅原因,这里不再详细介绍所有验证算例. 在流固耦合的交界面上,这里采用分区顺序耦合求解法,并利用加权余量法进行界面上数据的插值传递. 将流体的压力和黏性力作为面力载荷施加在固体上,而温度则作为体力载荷施加在固体网格中.
2 计算结果分析 2.1 流道插件的结构应力研究这里选择一种比较典型的设计,取流道插件厚度为5 mm,间隙流宽度则为8 mm,钢壁厚度为5 mm.同时假设流道插件为完全电绝缘,这种情况下结构较为危险,所以对这种情况进行具体的结构安全分析.
由于流道插件是用碳化硅复合材料制成的,这种材料的试验结果表明,其受拉和受压强度大[14],所以这里分开讨论拉、压应力. 另外,碳化硅复合材料中纤维的分布方向和数量均会影响其力学性能,所以在厚度和面内方向也采取不同的材料极限进行评判. 碳化硅复合材料的抗压能力远高于其抗拉能力.当材料受拉伸时,将在内部生成细微的小裂纹,由于其具有较好的界面结构,裂纹的扩散可以受到一定的抑制,当受压时,其内部的裂纹则可以重新闭合. 当拉、压应力不大的时候,碳化硅是可以当作线弹性和各项同性材料的[15]. 这里,采用表 2中列出的材料极限,可以看到拉应力的极限小于压应力极限,而因为厚度方向材料性能稍差,因此该方向上的极限低于面内极限.
|
|
表 2 碳化硅材料设计极限 Table 2 Design limits of SiC |
对于边界条件的选取,根据在实际包层中流道插件的安装情况,这里采用约束进口处极向位移、同时约束出口处环向和径向位移的方式. 初始参考温度为400 ℃. 计算结果说明流道插件在厚度方向有较大的温度梯度,而内壁温度更高.同时,由于各部分温升不一致,因此流道插件上会分布有不均匀的热应力.
对流道插件各方向的应力分析在图 2中列出. 图 2(a)为垂直于极向的面内应力分布图,其中哈特曼壁上显示的是径向应力,侧壁上显示的则是环向的应力. 从面内应力分布看,最大拉应力约为80 MPa,小于材料面内拉应力极限145 MPa,而面内最大拉应力约为260 MPa,同样远低于许用极限580 MPa. 图 2(b)为厚度方向应力分布图,其中哈特曼壁上显示的是环向应力,侧壁上显示的则是径向应力. 从厚度方向应力分布看,最大拉应力仅为约40 MPa,远低于厚度方向设计极限110 MPa,而压应力最大值也远低于设计极限420 MPa,因此,虽然厚度方向碳化硅的力学性能稍差,但在实际计算中发现厚度方向的正应力也较低,满足设计要求.

|
Download:
|
| 图 2 流道插件不同方向的应力 Fig. 2 Different stresses of FCI | |
图 2(c)为流动方向的应力分布图,即面内极向应力. 可以看出,在该方向上,结构是最为危险的. 其中最大压应力在许用范围之内,但最大拉应力约为160 MPa,已经稍高出面内拉应力极限145 MPa,最大拉应力值出现在靠近第一壁的侧壁和哈特曼壁交界的棱边上. 从Mises应力分布(图 2(d))看,最大应力主要集中在出口位移约束处,该算例中最大等效应力在设计极限内. 综合以上结论我们得到,流道插件厚度方向和面内的压应力较为安全,但极向面内拉应力需要引起注意.
2.2 材料热导率的影响碳化硅复合材料由于加工工艺的不同,可以得到不同的热导率,其范围在2~200 W/(m·K),热导率将直接影响到流道插件结构的绝热性能,同时影响到整个流场和结构场的温度分布,从而影响到流道插件的应力状态.
由于碳化硅在高温时的力学性能较为稳定,在1 200 ℃以下时,其弹性模量变化很小,因此在计算时选取固定的弹性模量.
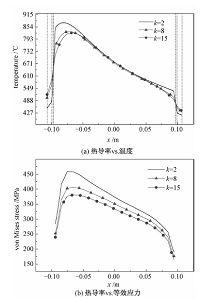
图 3为碳化硅取不同热导率时,出口截面的温度和哈特曼壁上的Mises应力分布.由图中可以看出,当碳化硅热导率取2 W/(m·K)时,流道插件热绝缘性能较好,这时钢壁上的温度会降低,同时出口温度较高,主流区中出口平均温度约为691 ℃,这对提高出口热效率有利. 从Mises应力分布可以看出,由于流道插件绝热性较好,提高了流道插件壁厚方向的温度梯度,从而使流道插件上的热应力较大. 当碳化硅热导率提高到8 W/(m·K)时,出口平均温度约669 ℃,而当碳化硅热导率提高到15 W/(m·K)时,出口平均温度变为665 ℃,降幅并不明显. 碳化硅具有较高的热导率时,钢壁温度更高,这时流道插件厚度方向温差较小,插件热应力更低.
|
Download:
|
| 图 3 不同热导率时的温度和等效应力分布 Fig. 3 Temperatures and Mises stresses with various SiC thermal conductivities | |
综合以上结论,碳化硅热导率增加时,出口平均温度会降低,对提高出口热效率不利,但这种影响在热导率超过8 W/(m·K)时较小. 同时,热导率提高会增加钢壁上的温度,这对第一壁结构安全不利. 但是热导率提高会降低流道插件内外壁温差,降低流道插件的热应力,这对流道插件的结构安全是有利的.
3 结论1) 对于无压力平衡槽的流道插件来说,从厚度方向应力和面内方向的压应力来评判,应力均低于设计极限,而面内极向拉应力以及棱边处剪切破坏是导致插件结构破坏的主要原因. 考虑碳化硅材料良好的损伤容忍性以及二次应力的自限性,在本文计算的范围内,流道插件结构在温度和磁流体压力作用下是基本安全的. 但我们在计算中发现,包层结构不同的几何特征以及材料物性参数,会对流道插件结构应力产生很大的非线性影响,因此对于包层结构的设计仍需进行详细的分析和优化工作.
2) 流道插件作为热绝缘部件,应具有较低的热导率. 计算结果表明,当碳化硅热导率较低时,其有利影响包括:出口金属流体的平均温度更高,从而得到更高的热效率;可以更好地隔绝主流区向钢壁的热传递,保证第一壁的结构安全. 但同时,流道插件自身的温度梯度将会增大,使流道插件内部产生较高的热应力. 而对于流道插件来说,热应力远高于金属流体压力带来的一次应力,是影响结构安全的最主要因素,因此,在选取流道插件厚度和热导率等参数时,应综合考虑磁流体压力降、传热效率、第一壁和流道插件的结构安全等因素.
| [1] | Holtkamp N. An overview of the ITER project[J]. Fusion Engineering and Design , 2007, 82 :427–434. DOI:10.1016/j.fusengdes.2007.03.029 |
| [2] | Wong C P C, Abdou M, Dagher M, et al. An overview of the US DCLL ITER-TBM program[J]. Fusion Engineering and Design , 2010, 85 :1129–1132. DOI:10.1016/j.fusengdes.2010.02.021 |
| [3] | Smolentsev S, Moreau R, Bühler L, et al. MHD thermofluid issues of liquid-metal blankets: phenomena and advances[J]. Fusion Engineering and Design , 2010, 85 :1196–1205. DOI:10.1016/j.fusengdes.2010.02.038 |
| [4] | Wang H, Tang C. Preliminary analysis of liquid LiPb MHD flow and pressure drop in DWT blanket of FDS-I[J]. Fusion Engineering and Design , 2012, 87 :1501–1505. DOI:10.1016/j.fusengdes.2012.03.043 |
| [5] | Smolentsev S, Morley N B, Wong C, et al. MHD and heat transfer considerations for the US DCLL blanket for DEMO and ITER TBM[J]. Fusion Engineering and Design , 2008, 83 :1788–1791. DOI:10.1016/j.fusengdes.2008.04.002 |
| [6] | Vitkovsky I, Golovanov M, Divavin V, et al. Neutronic, thermal-hydraulic and stress analysis of RF lithium cooled test blanket module for ITER[J]. Fusion Engineering and Design , 2000, 49 :703–707. |
| [7] | Sharafat S, Aoyama A, Morley N, et al. Development status of a SiC-foam based flow channel insert for a US-ITER DCLL TBM[J]. Fusion Science and Technology , 2009, 56 :883. |
| [8] | Sharafat S, Aoyama A, Ghoniem N, et al. Heat testing of a prototypical SiC-foam-based flow channel insert[J]. Plasma Science, IEEE Transactions on , 2010, 38 :2993–2998. DOI:10.1109/TPS.2010.2058867 |
| [9] | Ying A, Abdou M, Zhang H, et al. Progress on an integrated multi-physics simulation predictive capability for plasma chamber nuclear components[J]. Fusion Engineering and Design , 2010, 85 :1681–1688. DOI:10.1016/j.fusengdes.2010.05.015 |
| [10] | Smolentsev S, Morley N, Abdou M. Magnetohydrodynamic and thermal issues of the SiC~ f/SiC flow channel insert[J]. Fusion Science and Technology , 2006, 50 :107–119. |
| [11] | Ni M J, Munipalli R, Morley N B, et al. A current density conservative scheme for incompressible MHD flows at a low magnetic Reynolds number. Part I: On a rectangular collocated grid system[J]. Journal of Computational Physics , 2007, 227 :174–204. DOI:10.1016/j.jcp.2007.07.025 |
| [12] | Ni M J, Munipalli R, Huang P, et al. A current density conservative scheme for incompressible MHD flows at a low magnetic Reynolds number. Part Ⅱ: On an arbitrary collocated mesh[J]. Journal of Computational Physics , 2007, 227 :205–228. DOI:10.1016/j.jcp.2007.07.023 |
| [13] | Ni M J, Li J F. A consistent and conservative scheme for incompressible MHD flows at a low magnetic Reynolds number. Part Ⅲ: On a staggered mesh[J]. [J]. Journal of Computational Physics, , 2012, 231 :281–298. DOI:10.1016/j.jcp.2011.08.013 |
| [14] | Aiello G, Giancarli L, Golfier H, et al. Modeling of mechanical behavior and design criteria for SiCf/SiC composite structures in fusion reactors[J]. Fusion Engineering and Design , 2003, 65 :77–88. DOI:10.1016/S0920-3796(02)00212-0 |
| [15] | Riccardi B, Fenici P, Frias Rebelo A, et al. Status of the European R&D activities on SiCf/SiC composites for fusion reactors[J]. Fusion Engineering and Design , 2000, 51 :11–22. |
 2016, Vol. 33
2016, Vol. 33 


