在复射影空间上轨道问题是第一个不平凡的轨道研究问题.在这个问题上Bando和Ohnita^[1]讨论CPⁿ中的齐性二维球面,给出奠基性的成果,为后人广泛引用,也被平行推广得到很多结论,见文献^[2-5].但他们的研究手法偏于用李代数或者微分方程,对群作用的不变多项式为零所能判别的某个一元n次方程的根重数和根分布的结果可决定轨道维数,这一观点没有指出.在复射影空间的SU(2)三维轨道上,也缺乏正面表达的结论.

本文从根分布的角度给出Bando-Ohnita对齐性二维球面分类结果的更加明显的刻画,求出了决定齐性二维球面的SU(2)轨道的李群多项式表示的显式表达式.证明复射影空间中SU(2)轨道的维数取决于一个对应的扩大复平面系数上的一元n次方程的重根和负共轭倒数根对分布.把SU(2)轨道维数归结为黎曼球面上n个点是否重合或成为对径点的问题.这为SU(2)轨道的深入研究提供了新方法.另一方面对SU(2)三维轨道也初步研究了其性质好坏与根分布的关系.

1 SU(2)的复表示

在这一节中,我们将采用与文献^[3]中相同的一些符号记法.下边先回顾SU(2)不可约表示的一些基本性质.

SU(2)定义为

$SU\left( 2 \right)\left\{ g=\left( \begin{matrix} a & -\overline{b} \\ b & \overline{a} \\ \end{matrix} \right) \right\};a,b\in C,{{\left| a \right|}^{2}}+{{\left| b \right|}^{2}}=1$

接着,考虑SU(2)的复表示.令V_n为一个(n+1)维的复向量空间,它由关于变量z₀和z₁的n次齐次多项式构成.在 V_n定义一种Hermitian内积(,),使得

$u_{k}^{\left( n \right)}=\frac{1}{\sqrt{k!\left( n-k \right)!}}z_{0}^{n-k}z_{1}^{k};0\le k\le n$

是V_n的一组酉基.由此,定义实内积为〈,〉=Re(,).SU(2)在V_n的不可约复表示ρ_n定义为:

${{\rho }_{n}}\left( g \right)p\left( {{z}_{0}},{{z}_{1}} \right):p\left( a{{z}_{0}}+b{{z}_{1}},-\overline{b}{{z}_{0}}+\overline{a}{{z}_{1}} \right)$

(1)

其中g∈SU(2),p∈V_n. 因为ρ_n(g)u⁽ⁿ⁾_k∈V_n,可以记

${{\rho }_{n}}\left( g \right)u_{k}^{\left( n \right)}=\sum\limits_{i=0}^{n}{\lambda _{k}^{i}\left( a,b \right)u_{i}^{\left( n \right)}}$

其中

$\begin{align} & \lambda _{k}^{i}\left( a,b \right)=\sqrt{\frac{i!\left( n-i \right)!}{k!\left( n-k \right)!}\mu }, \\ & \mu =\sum\limits_{h+r=n-i}{\left( \begin{matrix} n-i \\ h \\ \end{matrix} \right)\left( \begin{matrix} i \\ r \\ \end{matrix} \right){{a}^{h}}{{\left( \overline{a} \right)}^{k-r}}{{b}^{n-k-h}}{{\left( -\overline{b} \right)}^{r}}.} \\ \end{align}$

(2)

我们将V_n等同于(n+1)维复向量空间Cⁿ⁺¹,在这种等同下,每一个线性自同态ρ_n(g)都可以由矩阵(λⁱ_k(a,b))来表示,于是有李群同态:

$\begin{align} & {{\rho }_{n}}:SU\left( 2 \right)\to U\left( n+1 \right) \\ & g\mapsto {{\rho }_{n}}\left( g \right)=\left( \lambda _{k}^{i}\left( a,b \right) \right). \\ \end{align}$

(3)

2 复射影空间的SU(2)轨道与一元n次方程根集的关系

为使上一节介绍的李群多项式表示成为一个变元,我们引入扩大复平面S²=C∪∞来紧化复数域,对多项式表示空间也重新约定:用扩大复平面上的一元n次复变量z的多项式全体表示Cⁿ⁺¹,用其上的多项式在非零常复数倍下的等价类[f]来表示CPⁿ,则[f]由该多项式的零点集合完全确定.低于n次的是退化的情形,也可写成n个因子相乘,有些因子退化成0z+1认为根是无穷大.在次数为k时,认为有n-k重根是∞.此外,定义SU(2)在CPⁿ上的作用为$\left( \begin{matrix} a & b \\ -\overline{b} & \overline{a} \\ \end{matrix} \right)\left[ f\left( z \right) \right]\tilde{\ }\left[ {{\left( -\overline{b}z+\overline{a} \right)}^{n}}f\left( \left( az+b \right)/\left( -\overline{b}z+\overline{a} \right) \right) \right]$,其中a,b是复数,满足|a|²+|b|²=1.以下不加证明地提示一些扩大复平面的这种分式线性变换的重要性质.

引理2.1 满足a,b是复数,|a|²+|b|²=1的分式线性变换$z\mapsto \left( az+b \right)/\left( -\overline{b}z+\overline{a} \right)$有下列性质:

1) 它们形成一个群.且在分式线性变换的复合作群乘法下同构SU(2)矩阵群.

2) $b/a,b/\overline{a}$都可以取到任何固定的复数.

3) 任意2个扩大复平面的数可以用这个群迁移.

4) 这个群可迁地作用在扩大复平面上,在每一点处的迷向群都是SU(2)的对角子群的共轭群在1)中同构的拉回群.

5) 在这个群作用下,扩大复平面是一个齐性空间.

3 球极投影的对径点与SU(2)作用的迷向群的关系

命题3.1 分式线性变换群$\left\{ \frac{az+b}{cz+b};a,b,c,d\in C \right\}$与σ(z)=-1/z生成的群元都是扩大复平面的自同构,但存在扩大复平面的一个度量,使得分式线性变换中保持这个度量的只有a=d[TX-],c=-b[TX-]的子群与σ(z)=-1/z生成的群.且在扩大复平面到单位球的球极投影下,这个子群是单位球上的保距变换.特别地,$\tilde{\sigma }\left( z \right)=-1/\overline{z}$, 在球面上的诱导变换是球面的对径点之间的置换.且如下交换图成立:

交换立方图的上层是扩大复平面内的变换,下层是单位球,上下层之间的映射是球极映射.

证明 以单位球面2点间的弦长为距离,拉回到扩大复平面可写出一个度量的表达式: 单位球面上两点P和P',对应扩大复平面上z和z'; P和P'的欧氏距离为$d\left( p,p' \right)=2\left| z-z' \right|/\left( \sqrt{1+{{\left| z \right|}^{2}}}\sqrt{1+{{\left| z' \right|}^{2}}} \right)$断言这是符合命题的度量.

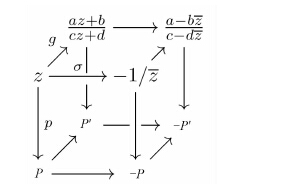
写z=x+yiz在球极投影下对应(2x/(1+|z|²),2y/(1+|z|²),(|z|²-1)/(1+|z|²)).由此,-1/z对应-(2x/(1+|z|²),2y/(1+|z|²),(|z|²-1)/(1+|z|²)),是对径点.无穷大∞,对应北极(0,0,1).故复数的负共轭取倒是与球面对径点对应的. 简单的计算可验证图交换.

现在再看多项式表示空间的多项式的根,根在球极投影到单位球面上的相对位置相同(即任意两根对应点的距离相同,则它们之间是可以用引理2.1中的分式线性变换互相迁移的,也就是会在ρ(SU(2))作用下的同一轨道上.同一轨道上,每个点对应球面上的n个点相互距离是一样的(至多差一顺序).轨道的所有几何量可通过n个点相互距离计算出来.

对Bando-Ohnita^[1]关于齐性二维球面(严格讲不是忠实的SU(2)轨道,而是SU(2)/S¹轨道)的结论,将 Cⁿ⁺¹的多项式表示的基底记为$u_{k}^{\left( n \right)}={{z}^{k}}\sqrt{k!\left( n-k \right)!}$ 那么[z^n-k]的对径点(将根映到单位球面取对径的拉回)就是[z^k]. 运用我们的语言表达和证明如下:

设V_n为变量z的次数不超过n的多项式构成的(n+1)维的复向量空间,在V_n上定义酉积使得u⁽ⁿ⁾₀,…,u⁽ⁿ⁾_n是其一组酉基,其中$u_{k}^{\left( n \right)}={{z}^{k}}/\sqrt{k!\left( n-k \right)!}$. 记S²ⁿ⁺¹={v∈Vⁿ;<v,v>=1}.在S²ⁿ⁺¹上定义等价类~如下: f~f'当且仅当f=cf',其中c是常数.令CPⁿ=S²ⁿ⁺¹/~.在CPⁿ上取Fubini-Study度量,使得自然投影π:S²ⁿ⁺¹→CPⁿ为黎曼淹没.

定理3.1 SU(2)在CPⁿ作用下的一个轨道M是浸入CPⁿ的2维轨道当且仅当M=π(ρ(SU(2))u⁽ⁿ⁾_k.该基点在CPⁿ中的轨道在多项式空间Vⁿ内的表示是$\left[ {{\left( z-c \right)}^{k}}{{\left( \overline{c}z+1 \right)}^{n-k}}/\sqrt{k!\left( n-k \right)!} \right]\cup \left[ {{z}^{n-k}}/\sqrt{k!\left( n-k \right)!} \right]$,这里1≤k≤n-1,k=0或n时,轨道是 $\left[ {{\left( z-c \right)}^{n}}/\sqrt{n!} \right]\cup \left[ 1 \right]$,c是一个复数.

证明 由于 $\left[ {{\left( z-c \right)}^{k}}{{\left( \overline{c}z+1 \right)}^{n-k}}/\sqrt{k!\left( n-k \right)!} \right]\cup \left[ c{{z}^{n-k}}/\sqrt{k!\left( n-k \right)!} \right]$是由SU(2)中的元素$1/\sqrt{1+{{\left| c \right|}^{2}}}\left( \begin{matrix} 1 & -c \\ \overline{c} & 1 \\ \end{matrix} \right)$作用在z^k上的轨道的多项式表示. c=∞时对应的是-1/z的变换,得到z^n-k.这个轨道是二维的原因是,它的根在黎曼球上对应的点要么重合要么是对径点. 若有对径点对,则其决定了一条轴线,绕这轴线的旋转是固定这些根不变的作用,正好是一个S¹作用,即SU(2)作用的迷向群为S¹.故为二维轨道.若无对径点对,则全汇聚在一个点,这时对应k=0或n的情形.得到的是一条全纯曲线.总之都是实二维的.

Bando-Ohnita的结论中有一种特殊情况,即n=2k对径点重数都是k.此时迷向群有2个分支,一个分支是保持对径点不动,即旋转群S¹,另一个分支就是交换对径点.我们如果不用上述二维上的基点,由于取法不受限制,总能取到对应球面上的n个点线性无关的.这n个点的自同构有限.迷向群是有限群.此时基点对应轨道是三维.这也是下面的章节能够讨论三维轨道的原因. 总结以上分析和论证,得到如下的定理.

定理3.2 在没有标明映射的地方存在自然诱导的映射,符号同前,下图交换:

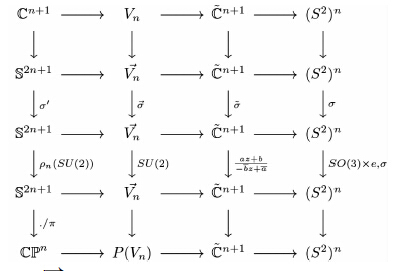
其中,$\overset{\to }{\mathop{{{V}_{n}}}}\,$为V_n中的系数向量的酉积为1的规范化的一元多项式. S²是单位球面,坐标分量用(x,y,z)表示,则$,是被它们诱导的映射.第1列第2列的映射是乘酉正交化后的多项式基底向量形成多项式,第2列到第3列是取多项式根,第3列到第4列是球极投影.

4 SU(2)三维轨道的初探

SU(2)作用的不变量由分式线性变换在黎曼球上的作用可以观察到,是作用前的多项式的根对应的黎曼球上的n个点(算上重点)的相对位置关系.如果n个点有一维的自同构群那么因为SU(2)自身是3个自由度的,得到的轨道将是二维.反之就是三维的轨道.这节更关心的是如何在多项式的系数空间里用曲面把决定三维轨道的那些基点描出来.

引理4.1 关于t的复系数一元二次方程$x{{t}^{2}}/\sqrt{2}+yt+z/\sqrt{2}=0$的两根呈负共轭倒数的判别条件是$\left| \Delta \right|=\left| {{y}^{2}}-2xz \right|={{\left| x \right|}^{2}}+{{\left| y \right|}^{2}}+{{\left| z \right|}^{2}}$.(用结式可证明).

命题4.1 在CP²情况下,用酉模为1的多项式系数空间S⁵的复坐标(x,y,z)来描叙SU(2)轨道,则过单位酉模基点(x₀,y₀,z₀)的轨道是三维轨道等价于|y²₀-2x₀z₀|≠0,或1. 证明 定理3.1已经证明系数向量属于轨道是二维的基点的充要条件是其轨道过基点(1,0,0),(0,1,0)或(0,0,1).这三者的判别式要么是0要么是1.下面只需证非0,1的点不可能与这3个基点共轨道(引理4.1).此时方程的根在单位球面上对应的两点不是对径点也不重合,其自同构是有限群,故基点处SU(2)作用下的迷向群离散从而为三维轨道.

引理4.2 单位酉模的多项式系数空间S²ⁿ⁺¹上有n-k重根为z,另外k重根为-1/z的多项式系数的参数表示为$\frac{\sqrt{k!\left( n-k \right)!{{\left( 1+{{\left| z \right|}^{2}} \right)}^{n}}}}{-{{\overline{z}}^{k}}{{e}^{i\theta }}}\left( 1,-{{\delta }_{1}},{{\delta }_{2}},\cdots ,{{\left( -1 \right)}^{k}}{{\delta }_{k}},\cdots ,{{\left( -1 \right)}^{n}}{{\delta }_{n}} \right)$,其中δ_k,是关于n-k重根z,k重根-1/z的初等对称多项式,且δ_k,可以写成f(|z|²)/z^k,f是有理多项式.特别地,n=2k时,θ=0成立,这就是说,在模S¹作用后,它的参数是全实有理参数.

证明 只证(1,-δ₁,δ₂,…,(-1)^kδ_k,…,(-1)ⁿδ_n)的模是$\frac{{{\left| z \right|}^{k}}}{\sqrt{k!\left( n-k \right)!{{\left( 1+{{\left| z \right|}^{2}} \right)}^{n}}}}$用定义来求酉内积对${{\left( {{\partial }_{1}}+1/z{{\partial }_{2}} \right)}^{k}}{{\left( {{\partial }_{1}}-\overline{z}{{\partial }_{2}} \right)}^{n-k}}{{\left( {{z}_{1}}+\frac{1}{\overline{z}}{{z}_{2}} \right)}^{k}}{{\left( {{z}_{1}}-z{{z}_{2}} \right)}^{n-k}}$做一对换元令$,把偏微分算子换成是关于g,h的.整理即得上面的结果.在n=2k的情况,考虑到$g={{\left( {{z}_{1}}+\frac{1}{\overline{z}}{{z}_{2}} \right)}^{k}},h={{\left( {{z}_{1}}-z{{z}_{2}} \right)}^{n-k}}$中令z=-b/a时多项式的首项-(ab)^k可由-1/ab=z+1/z算出,故而直接得到要证的结果,参数θ=0.□

注意到引理中的轨道只涉及一个变元z,分式线性变换可以把它迁移至任意扩大复平面的数,故有如下.

推论4.1 上述n-k,重根为z,另外k重根为-1/z决定的单位酉模参数代表的流形都是齐性流形.自同构群都是ρ_n(SU(2)),自同构群的作用都可迁移,且每点处的迷向群都是S¹的共轭群的表示群.

事实上,由文献^[6]中的到射影空间的嵌入的像是Zariski闭集的定理,这个流形可以用有限个代数方程的交表示出来.由于推论中的可迁移性,我们发现了一个非此即彼的论断:即在这些个方程交上的基点对应的就是二维轨道,不在它上面的就是三维轨道.这是命题4.1到CPⁿ的推广.

5 SU(2)三维轨道与重根分布的对应

我们引入一段方程重根的判别理论,根据$n=\sum\limits_{i=1}^{r}{{{n}_{i}}}$的不同的正整数分拆,扩大复平面系数上的含重根的一元n次方程的重根分布呈现(n₁,n₂,…,n_r)多种类型,即方程的根分别为n₁,n₂,…,n_r重. n₁重的x₁,n₂重的x₂,…,n_r重的x_r,x_i,x_j,1≤i,j≤n可以相等.如果将其中的某个n_i再次分拆成2个正整数之和(n_i-q)+q,那么对应的重根类型就会成为(n₁,n₂,…,(n_i-q),q…,n_r). 我们把这样的一个操作叫做一次加细,把加细的逆操作叫缩并. 一元n次方程的不同类型的重根分布对应什么样的判别式的问题,可以从如下嵌入来考虑:$\begin{align} & {{\left( C{{P}^{1}} \right)}^{r}}\to {{\left( C{{P}^{1}} \right)}^{n}}\to C{{P}^{n}}:\left( {{x}_{1}},{{x}_{2}},\cdots {{x}_{r}} \right)\xrightarrow{{{\Delta }_{{{n}_{1}}}}\times {{\Delta }_{{{n}_{2}}}}\times {{\Delta }_{{{n}_{r}}}}}\left( {{x}_{1}},{{x}_{1}},\cdots {{x}_{1}},{{x}_{2}},{{x}_{2}},\cdots ,{{x}_{r}},{{x}_{r}},\cdots ,{{x}_{r}} \right) \\ & \xrightarrow{f}\left( 1,-{{\delta }_{1}},\cdots ,{{\left( -1 \right)}^{k}}{{\delta }_{k}},\cdots ,{{\delta }_{n}} \right) \\ \end{align}$,其中δ_i是关于x₁,x₁,…,x₁,x₂,x₂,…,x₂,…,x_r,x_r,…,x_r,这n个根的初等对称多项式,$n=\sum\limits_{i=1}^{r}{{{n}_{i}}}$为不同的正整数分拆,为了使映射连续,x_i,x_j可以取为相等,1≤i,j≤n.那么f的像就成了一个首一一元n次方程的系数,其根为x₁,x₂,…,x_r,根的重数为(n₁,n₂,…,n_r).由于右边的嵌入是到复射影空间,故由文献^[6]得到这个嵌入的像是一个Zariski闭集,即可以写成有限个既约的代数方程的交,这个交定义的射影代数簇定义为一元n次方程的类型为(n₁,n₂,…,n_r)的射影判别式簇,记为V(n₁,n₂,…,n_r).那么最初定义的重根类型的一次加细,会诱导判别式簇的一次加细,加细的映射由某个n_i重的根分拆成两个重数分别为(n_i-q),q根(可以相等)而成.缩并也是指这个逆过程.

命题5.1 采用与上面同样的记号,V(n₁,n₂,…,n_r)的奇异点必是由x₁,x₂,…,x_r中某个x_i=x_j,1≤i,j≤n的缩并在f的像下给出的点.k重奇异点必是k次缩并后给出的f的像点.

证明 奇异点是Jacobian矩阵(∂(-1)^pδ_p/∂x_q)的秩较非奇异点小的点.用母函数的技巧,作矩阵乘积:$\sum\limits_{p=0}^{n}{\left( \partial {{\left( -1 \right)}^{p}}{{\delta }_{p}}/\partial {{x}_{q}} \right){{x}^{p}}=\partial /\partial {{x}_{q}}\sum\limits_{p=0}^{n}{{{\left( -1 \right)}^{p}}{{\delta }_{p}}{{x}^{p}}=}}\partial /\partial {{x}_{q}}\underset{i=1}{\overset{r}{\mathop{\prod }}}\,{{\left( x-{{x}_{i}} \right)}^{{{n}_{i}}}}.$.

若Jacobian矩阵较非奇异点的秩少1,则存在一列不全为零的常数c_q,使得$\sum\limits_{q=1}^{r}{{{c}_{q}}\left( \partial {{\left( -1 \right)}^{p}}{{\delta }_{p}}/\partial {{x}_{q}} \right)=0}$对任意p成立,故$\sum\limits_{q=1}^{r}{{{c}_{q}}\partial /\partial {{x}_{q}}\underset{i=1}{\overset{r}{\mathop{\prod }}}\,{{\left( x-{{x}_{i}} \right)}^{{{n}_{i}}}}=0}$,n_i是正整数,由x的任意性可以消去关于x的公因式,得到$\sum\limits_{q=1}^{r}{{{C}_{q}}{{c}_{q}}\partial /\partial {{x}_{q}}\underset{i=1}{\overset{r}{\mathop{\prod }}}\,{{\left( x-{{x}_{i}} \right)}^{{{n}_{i}}}}=0}$,其中C_q是求导后得到的某个正整数.不妨设c₁≠0,代入x=x₁后发现$\underset{i=2}{\overset{r}{\mathop{\prod }}}\,\left( x-{{x}_{i}} \right)=0$成立,这意味着必存在某个i在2到n之间,使得x₁=x_i.

若Jacobian矩阵较非奇异点的秩少2,则在原判别式的参数化中代入x₁=x_i后,转化为新的Jacobian矩阵,其秩较非奇异点的秩少1.导致新的缩并会出现.重复上述操作,得到k重奇异点是缩并k次得到的判别式簇上的点.□

命题5.2 扩大复平面上的一元n次方程的根中有一对呈负共轭倒数存在的条件可以用关于这个方程的系数的一个方程作等价条件给出,这个方程所代表的超曲面是有奇异性的,其第n-2重的奇异点也就是重数最高的奇异点作为基点时对应的SU(2)轨道是二维的,且除全纯曲线外的二维轨道的基点只有这么多.其他点对应的轨道都是三维的.

证明 由该方程,以及做过z到-1/z的变换的方程作结式所得的关于系数的方程,即是这个方程的根有一对呈负共轭倒数存在的充要条件.按照上述引理,选只有一对呈负共轭倒数且没有其他等根的根分布对应的超曲面上的点,作缩并对应的投影映射,n-2次后才会投影到全是z与-1/z型的根对应的超曲面上的点上.此时这些点作为基点时对应的SU(2)轨道是二维的.没有缩并到这个程度的根在单位球面上对应的点的自同构群有限,故为三维.□