2. 中国科学院生态环境研究中心, 北京 100085
2. Research Center for Eco-Environmental Sciences, Chinese Academy of Sciences, Beijing 100085, China
目前,全球有大约500座活火山,其中有近70座在水下,其余均分布在陆地上[1]。地球上几乎每年都有规模和程度不同的火山喷发,给人类活动.和生存带来很大危害.过去15年内火山活动造成29 000多人死亡,迫使83万人离开自己的家园,经济损失超过30亿美元[1].火山喷发,特别是裂隙式喷发,熔岩流经过的地域多,覆盖面积大,造成危害也很严重.
岩浆在流动和冷却过程中,有可能形成不同类型的熔岩洞.其中规模较大而又普遍存在的是熔岩管(lava tube),它们往往会造成一些次生灾害.图 1为一熔岩管照片.通常,熔岩管里的熔岩可以在不被观察和检测到的情况下,到达比表面流动的岩浆更远的距离,并且会在距离火山喷发出口许多公里外的一些临时形成的出口喷出,这对于某些火山灾害区域的居民以及所有生物来说都是一种具有极大不确定性的安全隐患.老的熔岩管也可能坍塌.因此,确定熔岩管的存在和稳定性对于某些特定地区的火山灾害的评估非常重要.

|
Download:
|
| 图 1 熔岩管内部结构及上部坍塌形成的天窗 Fig. 1 Lava tube interior structure and the skylight caused by collapse of the upside | |
同时,目前已经发现月球、火星表面存在许多熔岩管[2],这些洞穴可以保护人类免受高温和严寒、高强度紫外线和宇宙射线辐射、陨石撞击以及火星上的沙尘暴等威胁.人类或许可以利用月球、火星上的熔岩管建立基地,探索宇宙.而且,在火星上发现的熔岩管洞穴还可能保存有火星原始生命存在的证据.因此,对地球上熔岩管应力状态和稳定性的研究可以作为人类探索宇宙的基础性工作.
20世纪以来,国内外科学家一方面通过野外考察和测量,对岩浆的各种物性参数给出更加真实准确的估计;另一方面根据实地观测以及数值模拟的方法,对熔岩管的形成机制进行了大胆的预测和分析.目前,对于熔岩管的形成过程,大体上可以归纳成以下2种:
1) 熔岩流内部流变形成“移动的圆柱”,排空之后形成熔岩管.这是由Ollier和Brown[3]共同提出的熔岩管形成机制,并且在对其的解释中,作者提出熔岩分层形成“层状熔岩”的概念;
2) 开放的熔岩隧道“封顶”后,内部岩浆排空形成熔岩管[4-7].相对而言,火山学家对该机制的研究更多,Dragoni等[6]和Tallarico与Dragoni[7]分别对熔岩河宽度较宽情况下熔岩管的“封顶”过程做出解释,认为岩浆冷却过程中,熔岩流中部区域优先发育成固体壳,进而向两端延伸直至与熔岩流两岸的熔岩碛相结合.而Valerio等[4]针对熔岩河宽度较窄的情况提出另一种洞顶形成的过程,即此时岩浆从熔岩流两岸开始冷却,进而向中心延伸,直至两侧固体壳相结合,完成“封顶”作用.
熔岩管应力状态、稳定性及形成过程中的影响因素,对于熔岩管安全性评估以及其他星球熔岩管的探索非常重要.很多火山学家之前做了大量熔岩流动和熔岩管形成过程的研究,但是关于熔岩管应力状态的工作比较稀少.特别是熔岩从约千度的高温冷却时热应力的作用缺少定量研究.不同大小、深度以及不同形状的熔岩管,其形成过程中的热应力有什么差别?这些因素对于熔岩管的安全稳定性有什么样的影响? 本文通过数值计算的方法对熔岩管的形成过程进行模拟,计算过程做了一定的简化,即不考虑岩石的破裂过程,试图给出熔岩管形成过程中的热应力情况,进而对以上问题作出比较合理的分析与回答.
1 定性分析当熔岩管开始形成时,熔岩管附近的岩浆逐渐冷却,直到其强度可以抵抗洞内岩浆的拖曳力以及岩石自身的重力时,熔岩管的形状基本形成.此时,洞内的岩浆继续潜流,到岩浆流尽时,熔岩管内有2种可能的端元(end member)模型:一种是熔岩管与外界联通,管内最低温度与外界温度相同,即0 ℃;另一种是熔岩管未与外界联通,此时洞内温度并不会降低很多,而是保持在一个较高的温度上.由于第2种情况更为常见,因此,本文假设熔岩管区域内部充满了1 000 ℃炙热的空气和浮渣.随时间推移,岩浆冷却形成高温新岩石,其温度通过热传导而降低,我们考察由此过程产生的热应力情况,并主要着眼于熔岩管附近.
为简单起见,计算中并未考虑熔岩管在形成过程中岩石的破裂情况,即所采用的计算模型为完全理想化的模型.由于研究重点在于对不同类型的熔岩管的热应力情况作出分析,考察不同的参数对于熔岩管稳定性的影响,加之考虑到计算规模的大小以及复杂程度,因此这种简化是可以接受的.
本研究所使用的计算程序是由FEPG有限元程序自动生成系统生成的温度和变形耦合的程序,满足实际所要解决的熔岩管热应力问题,结果的图像绘制由GMT和MATLAB共同完成.
2 计算方法有限单元法(finite element method,FEM,)是一种求偏微分方程边值问题的常用数值方法,在处理地球物理问题中有其独特的优势,得到了广泛应用.石耀霖和王其允[8] 采用有限元方法对高喜马拉雅淡色花岗岩的形成进行热模拟研究,张健和石耀霖[9]利用有限元方法法对海岭俯冲的全过程进行热模拟,臧绍先和宁杰远[10]采用有限元法的准静态计算方案计算西太平洋俯冲带的温度场[10].
2.1 控制方程和物性参数我们借鉴前人经验,采用有限元法对所研究问题进行求解.本研究的特点是,应力的产生是由区域温度的变化引起,并且要求解的问题是一个热弹性问题,因此采用标准形式的热传导方程作为温度场的控制方程:
| $\rho c\frac{\partial T}{\partial t}=k{{\nabla }^{2}}T+A,$ | (1) |
其中,T为温度,t为时间,ρ为岩石密度,c为岩石比热容,κ为岩石的导热系数,A是热源项.
运用伽辽金有限元法求解该模型在温度变化过程中的位移场时,所用到的平衡方程为
| ${{\sigma }_{ji,j}}+{{f}_{i}}=0,i,j=1,2,3.$ | (2) |
这里采用张量的指标记法,并采用哑标的求和约定,1、2、3分别对应x、y、z(下同).其中,fx、fy和fz为3个方向的体力,因此fz代表所计算的玄武岩单位体积的重力.
这里,我们研究变温情况下熔岩管的热应力情况,所采用的热弹性方程为变温情况下的本构方程:
| ${{\sigma }_{i}}=22G{{\varepsilon }_{i}}+\lambda \theta -\frac{\alpha E\Delta T}{1-2\nu },i=1,2,3,{{\tau }_{ij}}=G{{\gamma }_{ij}},i,j=1,2,3,$ | (3) |
其中,σi为正应力,εi为正应变,τij为剪应力,γij为剪应变,G为剪切弹性模量,λ为拉梅弹性常数,θ为体积应变,α 为热膨胀系数,E为杨氏模量,ΔT为温度差,ν为泊松比.
计算中使用的物性参数主要参考Valerio等[4-5]在研究熔岩管形成机制时给出的值,岩石的物性参数见表 1.对于新岩石和老岩石,计算过程中采用相同的岩石参数进行求解.孔洞内充满了炙热的气体和浮渣,此时洞内热的传递以对流和辐射为主,用等效热导率200 W/m·℃和等效比热容量25 J/kg·℃来近似代替.
|
|
表 1 计算中使用的岩石物性参数 Table 1 Basalt parameters used in the calculation |
我们仅考虑熔岩流内部流变产生的熔岩管,并假定此时外部熔岩已经全部凝固,考察其后的温度变化以及相应的变形和应力变化情况.计算所采用的二维剖面模型如图 2所示,其中大片深绿区域为已经固化的老岩石,温度近似为0 ℃;正上方小片区域为新一期喷发中刚刚凝固的岩石,尽管凝固先后顺序不同温度会有差异,但温度大体接近固化温度,近似为1 000 ℃.

|
Download:
|
| 图 2 计算模型 Fig. 2 Calculation model | |
基于野外常见熔岩管的资料[4-7],新一期熔岩宽200 m,凸起10 m,下凹40 m.考虑一个距离地表 5 m,半径为5 m的熔岩管(图中圆孔).为减小边界条件不确定性对计算的影响,考虑的老岩石宽800 m,深300 m.计算中采用三角形网格,并且在洞壁附近加密.
2.3 初边值条件热传递问题的温度初始条件在老岩石区设为0 ℃,新凝固的熔岩和熔岩管内为1 000 ℃.边界条件在地表采用T=0 ℃的温度约束,两侧边界和下边界为绝热边界,即无热量的传递,由于侧边界和底边界远离熔岩管,在研究时段内对问题基本没有影响.计算中没有考虑地温梯度和地热流影 响,这是因为热传递问题为线性,计算的解与地温梯度稳态解叠加即得到完全解.由于300 m深 度上温差也不会大过10 ℃,与熔岩冷却的温度变化相比可以忽略不计,而且稳态地温不会造成热应力,对研究热应力问题没有影响.力学问题的边界条件在两侧边界采用垂直位移自由,水平位移约束,下边界位移约束为0;上边界和熔岩管内壁均使用自由边界,即正应力和剪切应力均为0.总计算时间约为160 a,时间步长取580 d左右,共计算100步.
3 模拟结果及讨论通过FEPG有限元程序对模型进行计算,可以得到熔岩管形成过程中温度场、位移场和应力场的分布情况.本文重点在于考察模型的热应力情况,从而可以对熔岩管的稳定性和安全性做出评估.下面分别对这3个场的模拟结果进行展示和分析.
3.1 温度场温度场的演变过程如图 3,图 3(a)—图 3(d)分别呈现出模型在第2、6、10以及36年时,温度场的分布情况.可以看出,新岩石区域的温度通过与外界冷空气和0 ℃老岩石区域的热传导作用而降低,整体热量呈现出向外及向下散发的趋势.与熔岩接触的部分老岩石开始因接触熔岩而温度升高,但随后也降低.

|
Download:
|
| 图 3 温度场的演变过程 Fig. 3 Temperature evolution | |
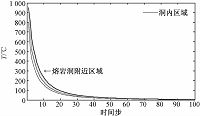
在该模型中,我们认为熔岩管内充满了炙热的空气和浮渣.此时,洞内热的传递方式以对流和辐射为主,洞内空气的密度很小,因此等效热容量很小,等效导热系数很大.故在开始阶段,洞内温度下降得比其周围区域更快,而随着时间的推移,熔岩管附近整体温度不断下降,最终,洞内温度和周围区域温度趋于一致,如图 4所示.其中,实线代表熔岩管内一点温度变化,4条虚线从左到右依次代表熔岩管上侧1.5 m、下侧1.5 m、左侧1.5 m和右侧1.5 m位置的温度变化.
|
Download:
|
| 图 4 洞内温度与相邻区域的温度变化曲线 Fig. 4 Temperature variation curves of lava tube and its adjacent areas | |
热弹性问题中,在一定的位移边界条件下,由于温度变化在弹性体内引起热胀冷缩从而产生的位移,等于在等温情况下由假想体力
| $\begin{align} & {{f}_{x}}=-\frac{\alpha E}{1-2\upsilon }\frac{\partial T}{\partial x}, \\ & {{f}_{y}}=-\frac{\alpha E}{1-2\upsilon }\frac{\partial T}{\partial y}, \\ & {{f}_{z}}=-\frac{\alpha E}{1-2\upsilon }\frac{\partial T}{\partial z}, \\ \end{align}$ |
和假想面力$\frac{\alpha ET}{1-2v}$作用下的位移,这里的T实际代表的是温差值[11].
在本问题的研究中,模型内部的位移变化基本可由热胀冷缩原理解释.新岩石部分通过与外界冷空气以及下方老岩石进行热传导作用,温度降低,因此呈现向下移动的趋势.而底部老岩石部分由于热量涌入,温度升高,会有轻微的膨胀.
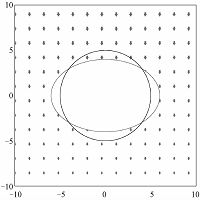
熔岩管附近位移向量分布如图 5所示,这里只选取模型的熔岩管附近区域(以熔岩管圆心为中心,边长20 m的正方形区域),其中圆形和椭圆形分别代表变形前后的熔岩管.为使变形的结果更加明显,这里把变形系数设置得较大.可以清楚地看出,熔岩管附近区域由于温度的显著降低,因此整体向下收缩,并且有较大的位移量,熔岩管由一个规则的圆形逐渐变成一个扁平的椭圆.
|
Download:
|
| 图 5 熔岩管附近位移和变形图 Fig. 5 Lava tube neighboring areas’ displacements and deformations | |
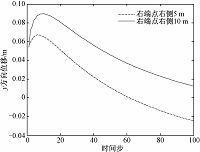
值得一提的是,在新岩石与老岩石交界线的左右两端点附近,开始阶段由于热传导而温度升高,因而有轻微隆起;随时间推移,该部分的温度又逐渐降低,因此又产生向下的位移量,呈现收缩趋势,如图 6所示.由于模型是左右对称的,因此这里只选取交界线右端点右侧5 m和10 m的区域.可以看出,此处位移变化并不十分明显.
|
Download:
|
| 图 6 交界线右端点右侧y方向位移 Fig. 6 The y-direction displacement on right side to boundary line’s right end point | |
熔岩管形成时的热应力状况是本文重点关注和讨论的内容.由于模型范围选取较大,而为了判断熔岩管是否稳定和安全,我们只需要考虑熔岩管附近的应力情况,因此下面只选取以熔岩管圆心为中心,边长20 m的正方形区域来做分析,并且只展示最后一个时间步的应力云图和矢量图.应力场所有结果图的色标均采用黄红为正,蓝色为负的表示方式,以使结果呈现更加明显.模型具有对称性,解答的各参量也具有对称性(或反对称性),表明我们的解答具有较高的精度.
1) 水平正应力σxx
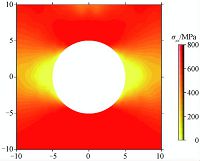
正应力σxx 的分布如图 7所示.很显然,熔岩管附近区域水平正应力均为拉应力.由于模型整体形状和热传导降温过程沿熔岩管中轴线对称,因此熔岩管两侧的应力情况基本一致.
|
Download:
|
| 图 7 正应力σxx分布云图 Fig. 7 Normal stress σxx cloud picture | |
在边界条件的设定上,模型的两侧边界水平位移限制为0,即左右边界不可以水平移动,因此整体变形只能上下滑动.当熔岩管附近区域温度降低时,根据热胀冷缩原理,该区域有向内部收缩的趋势.此时,由于外边界限定x方向位移为0,故熔岩管附近区域为拉应力.熔岩管左右两侧壁作为自由表面,其正应力σxx为0,因此两侧壁附近区域的应力σxx接近0,可以忽略.
2) 垂向正应力σyy
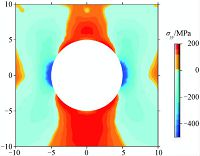
图 8展示的是最后一个时间步正应力σyy的分布云图.可以看出,在熔岩管左右两侧区域,压应力占主导作用,并且越靠近熔岩管,压应力越大;而熔岩管的顶部底部局部区域有拉应力.
|
Download:
|
| 图 8 正应力σyy分布云图 Fig. 8 Normal stress σyy cloud picture | |
造成这种现象的原因是,当熔岩管附近区域温度降低时,必然有向内部收缩的趋势,而在特定边界条件下,整个熔岩区域水平受到很大拉应力,熔岩管的整体变形,是由一个规则的圆形逐渐演化成一个扁平的椭圆.在此过程中,由于孔洞造成的应力集中必然会在造成熔岩管顶部和底部产生3倍于区域背景张应力的同时,在熔岩管左右两侧产生与区域背景张应力量级相当的压应力σyy.
结合水平向正应力σxx的分析可以发现,熔岩管顶部和底部附近正应力σyy的量级比该处σxx小很多.因此,如果熔岩管顶部和底部发生拉张破裂,其主要是受σxx控制,并且会形成倾角近乎垂直的张裂隙.
3) 剪应力σxy
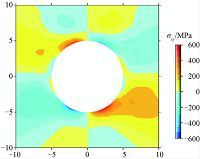
图 9展示的是最后一个时间步剪应力σxy的分布云图.容易发现,以熔岩管中轴线为对称轴,熔岩管左右两侧区域剪应力基本上大小相等,符号相反,即剪应力沿中轴线呈反对称分布.
|
Download:
|
| 图 9 剪应力分布云图 Fig. 9 Shear stress cloud picture | |
实际上,在变温情况下弹性体的应变由两部分叠加而成:①由于自由膨胀而引起的应变分量,即ε=αT,对应的剪应变分量为零;②在热膨胀时由于弹性体内各部分之间的相互约束而引起的应变分量,它们和热应力之间服从胡克定律[11].而模型区域在温度变化过程中不仅有体积上的变形,而且有形状上的变形(图 5),这必然会引起剪切应变,因此对应的剪应力不为零.
在模型的变形过程中,熔岩管从一个规则的圆形变成一个扁平的椭圆,而剪切应力会对这个变形过程做出一定贡献.以熔岩管口左上方区域为例,由于其所受剪切应力为正,因此该区域有向东北和西南方向拉张的趋势,而该趋势也恰好符合熔岩管的变形过程.其他3个象限的区域,其剪切应力同样也对该变形过程做出相应的贡献.容易看出,熔岩管附近的有4个剪切应力比较集中的位置,因此这些位置是最容易发生剪切破裂的地方.
4) 主应力
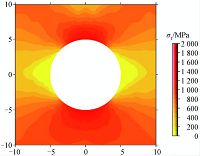
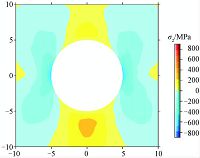
本研究着眼于熔岩管附近的热应力计算,进而判断周围岩石的破裂情况,由此分析熔岩管的稳定性和安全性.因此,对于主应力的计算和分析就显得尤为必要.通过最大主应力大小以及方向的计算,可以了解到熔岩管附近岩石最易破裂的部位及破裂方向,并且可以判断其是拉张破裂还是压缩破裂.图 10展示的是最后一个时间步最大主应力分布云图.可以看出,熔岩管上下两侧的最大主应力最大,且为拉张应力.左右两侧仍为拉应力,但是大小远远小于熔岩管上下两侧的最大主应力.图 11展示的是最后一个时间步最小主应力的分布云图.显然,熔岩管上下两侧最小主应力为拉应力,而左右两侧为压应力,并且熔岩管周围应力大小数量级相当.
|
Download:
|
| 图 10 最大主应力分布云图 Fig. 10 The maximum principal stress cloud picture | |
|
Download:
|
| 图 11 最小主应力分布云图 Fig. 11 The minimum principal stress cloud picture | |
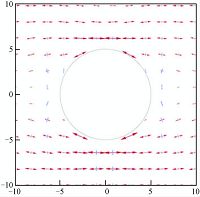
图 12展示的是最后一个时间步主应力分布的矢量图,红色箭头表示最大主应力,蓝色箭头表示最小主应力.可以看出,熔岩管边缘区域的最大主应力主要沿熔岩管截面的切线方向.结合最大主应力云图可知,熔岩管的上下两侧岩石更易发生破裂,且破裂类型为拉张破裂,受力方向基本沿熔岩管截面的切线方向.
|
Download:
|
| 图 12 主应力分布矢量图 Fig. 12 Principal stress vector | |
由图 12可知,熔岩管上下两侧最小主应力基本沿半径方向,而左右两侧基本沿熔岩管截面的切线方向.最小主应力的方向表示一点受拉或受压最轻微的方向,因此可以认为,在熔岩管上下两侧沿半径方向发生拉张破裂的可能性较小,而左右两侧沿熔岩管截面切线方向发生压缩破裂的可能性比较小.
实际上,岩石中包含有大量的微裂隙和空隙,这会直接削弱岩块的抗拉强度.相对而言,空隙对岩块的抗压强度影响就小得多.因此,岩块的抗拉强度一般远小于其抗压强度,也就是说,岩块更容易发生拉张破裂.通过本文之前的分析和展示不难发现,熔岩管口附近拉应力要比压应力更大,分布范围更广.因此,我们不妨主要着眼于熔岩管周围的拉应力区域.
熔岩管在形成过程中,熔岩管上下两侧始终保持拉应力状态,并且其数量级始终维持在一个比较高的水平.而通过最大主应力矢量图的展示,可以知道在熔岩管上下两侧,最大主应力基本沿熔岩管截面的切线方向.因此,可以得出结论,熔岩管最易发生拉张破裂的地方位于熔岩管上下两侧,并且受力方向基本沿熔岩管截面的切线方向.这个结论在一定程度上可以解释这样一种现象,即在实地考察的熔岩管中,其横截面附近区域的岩石裂痕,基本围绕熔岩管截面的切线方向分布.
4 不同类型熔岩管的稳定性分析基于野外常见熔岩管的资料,熔岩管内部的宽度在1~20 m,深度一般在地表下1~15 m不等,并且形状多样,其中以拱形、圆形以及椭圆形居多[4-7].通过对不同类型熔岩管形成过程中热应力的研究,可以对熔岩管的稳定性问题有一个全面的认识和把握,明确哪种类型的熔岩管更容易坍塌,哪种更稳定.未来在火星、月球上利用熔岩管建立探测基地时,究竟选用哪种类型的熔岩管安全系数更高,同样可以参考本文给出的结果.
图 13给出不同类型的熔岩管,其熔岩管附近区域最大主应力的趋势图,其中,横坐标为时间步,纵坐标为最大主应力值.通过上文分析可知,熔岩管最易发生破裂的地方是熔岩管的上下两侧,因此这里选取该区域为研究对象,虚线代表熔岩管上壁区域,实线代表熔岩管下壁区域.

|
Download:
|
| 图 13 不同类型熔岩管的最大主应力比较 Fig. 13 Comparison of the maximum principal stress among different kinds of lava tubes | |
图 13(a)代表之前所讨论的熔岩管,即截面为半径5 m的圆,顶板厚度为5 m,称为标准管;图 13(b)改变标准管的大小,将截面变为半径8 m的圆,顶板厚度保持不变,称为大管;图 13(c)改变标准管的深度,将顶板厚度设为8 m,截面圆的半径不变,称为深管;图 13(d)改变标准管的形状,将截面由原来半径5 m的圆变为一个长半轴6 m,短半轴4 m的横躺的椭圆,顶板厚度不变,称为椭圆截面管.
将大管、深管和椭圆截面管分别与标准管进行比较,可以得出不同类型熔岩管的相对稳定性.对于大熔岩管而言,无论是熔岩管上壁还是下壁区域,其所受到的最大主应力始终比小熔岩管更大,即大熔岩管更容易发生破裂.因此,相对而言,小熔岩管的稳定性更高,这与我们的直观感受是一致的.
对于不同深度的熔岩管来说,不论熔岩管上壁还是下壁区域,其受到的最大主应力,顶板厚度较小的熔岩管最后稳定的数值与顶板厚度较大的熔岩管相差不大.但是,在初始阶段,标准管最大主应力的增加速度与达到的最大值均比深管要大.因此,可以推断,埋深较深的熔岩管在形成过程中相对更稳定一些,其安全系数更高.
比较圆形截面和椭圆形截面的熔岩管可以发现,横截面为椭圆形的熔岩管受到的破坏力要显著地小于横截面为圆形的熔岩管.也就是说,前者在形成过程中更容易保持其形状的稳定性.
5 结论本文针对熔岩管形成机制建立熔岩管形成后温度演化过程和相应的位移和热应力状况,并且讨论不同类型熔岩管的稳定性和安全性问题.
目前野外实际考察所观察到的熔岩管大多数横截面积为类圆形,因此本文的结论可以适用.通过之前的分析可以看出,熔岩管最易发生破裂的地方位于熔岩管上下两侧,并且破裂类型为拉张破裂,受力方向基本沿熔岩管截面的切线方向.大熔岩管相较于小熔岩管更易坍塌,埋深较深的熔岩管比埋深较浅的熔岩管安全性更高,横躺的截面为椭圆形的熔岩管相对于圆形截面的熔岩管来说更加稳固,不易破裂.
通过以上结论,可以对某些地区的火山灾害进行更加精确的评估,将地表之下熔岩管的安全稳定性问题纳入考虑,并且未来在月球、火星建立基地时,也可以此来判断何种熔岩管更适合人类移居.
实际上,熔岩管在冷却过程中会不断发生破裂产生裂隙,而这些裂隙会影响熔岩管附近应力的分布和进一步的变形.在有限元计算中,研究张裂隙破裂,或工程中的开挖造成的应力变化,利用“杀死单元”(kill element)——即假定裂开或挖走的单元杨氏模量降为0,是一种得到广泛应用的方法.本文针对熔岩管的冷却做了初步的计算,目前尚未考虑岩石破裂引起的相关效应,笔者在进一步的研究中计划将杀死单元法引入计算程序,进而考虑这一影响因素.
| [1] | 洪汉净, 郑秀珍, 于泳, 等. 全球主要火山灾害及其分布特征[J]. 第四纪研究 , 2003, 23 (6) :594–603. |
| [2] | Bostonl P J. Lava tubes as analogue repositories for life, geochemistry, and climate records on Mars[J]. Analogue Sites for Mars Mission , 2011 :6027–6037. |
| [3] | Ollier C D, Brown M C. Lava caves of Victoria[J]. Bulletin of Volcanology , 1965, 28 (1) :215–229. DOI:10.1007/BF02596928 |
| [4] | Valerio A, Tallarico A, Dragoni M. A model for the formation of lava tubes by the growth of the crust from the levees[J]. Journal of Geophysical Research: Solid Earth (1978-2012) , 2010, 115 :B09208. |
| [5] | Valerio A, Tallarico A, Dragoni M. Mechanisms of formation of lava tubes[J]. Journal of Geophysical Research: Solid Earth (1978-2012) , 2008, 113 :B08209. |
| [6] | Dragoni M, Piombo A, Tallarico A. A model for the formation of lava tubes by roofing over a channel[J]. Journal of Geophysical Research: Solid Earth (1978-2012) , 1995, 100 (B5) :8435–8447. DOI:10.1029/94JB03263 |
| [7] | Tallarico A, Dragoni M. A three-dimensional Bingham model for channeled lava flows[J]. Journal of Geophysical Research: Solid Earth (1978-2012) , 2000, 105 (B11) :25969–25980. DOI:10.1029/2000JB900201 |
| [8] | 石耀霖, 王其允. 高喜马拉雅淡色花岗岩形成的热模拟[J]. 地球物理学报 , 1997, 40 (5) :667–676. |
| [9] | 张健, 石耀霖. 活动梅岭俯冲对岛弧地质过程的影响[J]. 地质力学学报 , 1997, 3 (2) :1–10. |
| [10] | 臧绍先, 宁杰远. 西太平洋俯冲带的研究及其动力学意义[J]. 地球物理学报 , 1996, 39 (2) :188–202. |
| [11] | 徐秉业, 刘信声. 应用弹塑性力学[M]. 北京: 清华大学出版社, 1995 . |
 2016, Vol. 33
2016, Vol. 33 


