波导系统中研究电磁波/光的传播性质时,经常利用TM/TE波进行偏振态描述[1],它们通常是根据电场矢量E或磁场矢量H是否仅存在横向分量来区分.当E只存在相对电磁波传播方向的横向分量时,称为TE波;同样,当H只存在横向分量时,称为TM波.这与波导和光纤通信领域对偏振态的定义是完全一致的,但有些学者会发现这种规定与二维光子晶体中传导波的偏振态定义却是完全相反的.二维光子晶体中,光沿垂直于介质柱方向入射,当E平行于组成光子晶体的介质柱时,虽然E仅存在垂直于传播方向的横向分量,却被称为TM波;而当H平行于组成光子晶体的介质柱时,虽然H只存在垂直于传播方向的横向分量[2],却被称为TE波.金属/介质界面上传播的表面等离子体波(spp)只存在一种TM偏振模式,不能以TE波的形式存在[3].《光学》教材[4]中讨论光在两种各向同性介质界面的反射与折射时,采用s态和p态来描述光的偏振态,任一光矢量可以被正交分解为s态和p态,而两种状态又分别对应着TE和TM偏振态.另外,在晶体光学的晶体双折射现象中,寻常光o光和非寻常光e光都是线偏振光,它们与TE/TM偏振模式和s/p态之间又存在什么关系呢?通过以上描述我们发现在不同传导系统中波的偏振态定义各不相同,产生这些问题的根本原因是什么?难道仅仅是定义不同吗?本文就从电磁场理论出发,通过数学推导对不同传导系统中电磁波偏振态的产生原因及其物理意义进行深入分析和归纳.研究发现任何传导系统中TM/TE偏振态都是满足Maxwell方程组的相互独立的方程解,都是以波导系统的偏振态定义为基础演变而来的.
1 光波的基本理论光波是一种电磁波,是电磁扰动的传播形式.电磁波是横波,电场强度矢量和磁场强度矢量的振动方向与波的传播方向垂直.其波动性可以通过麦克斯韦方程组进行描述,在不考虑自由电荷和传导电流的情况下,国际单位制中的麦克斯韦方程组表示
| $\left\{ \begin{matrix} \Delta \cdot D=0, \\ \Delta \cdot B=0, \\ \Delta \times E=-\frac{\partial B}{\partial t}, \\ \Delta \times H=\frac{\partial D}{\partial t}, \\ \end{matrix} \right.$ | (1) |
根据物质方程D=εE,B=μH,其中μ和ε分别为传播介质的磁导率和介电常数,通过对方程组(1)中第3式取旋度,代入第4式,再利用矢量解析公式和第1式可以推得E和H的波动方程,
| $\left\{ \begin{matrix} {{\Delta }^{2}}E-\frac{{{n}^{2}}}{{{c}^{2}}}\frac{{{\partial }^{2}}E}{\partial {{t}^{2}}}=0, \\ {{\Delta }^{2}}H-\frac{{{n}^{2}}}{{{c}^{2}}}\frac{{{\partial }^{2}}H}{\partial {{t}^{2}}}=0. \\ \end{matrix} \right.$ | (2) |
由于任意波形都可以看作是简谐波的叠加,为方便研究,可以取简谐波的特解进行分析.若考虑沿位移矢量r方向行进的波,该特解可以表示为Ψ(z,t)=Ψ0 cos(k·r-ωt),其中k称为波矢,其方向指向波前(等相位面)的传播方向,与波前的法线方向平行,其数值k=2π/λ被称为波的传播常数. 如果用矢量复波函数表示平面波的解,这时E和H中都包含复数相位因子expi(k·r-ωt),将其代入公式(1)整理可得
| $\left\{ \begin{matrix} k\times E={{\mu }_{0}}\omega H, \\ H\times k=\omega D, \\ \end{matrix} \right.$ | (3) |
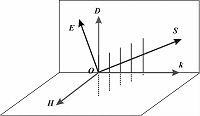
可以看出:H⊥E和k,D⊥H和k,所以D、H、k组成一右手正交坐标系.由电磁学可知,能流密度矢量S=E×H,E、H、S也组成一右手正交坐标系.由此可以推断D、k、E、S都垂直于H,所以它们都位于同一个垂直于H的平面内. 因为k⊥D,S⊥E,在各项同性介质中,ε为一常数,D、E同向,所以k、S同向.而在各向异性介质中,ε为一张量(数学表示为矩阵),D、E一般不同向,所以k、S也不同向. 图 1给出各向异性介质中k、D、E、H、S各矢量的关系,需要注意的是S的方向为光波能流方向,即光的传播方向,而k的方向为等相位面的法线方向,所以通常二者并不同向.
|
Download:
|
| 图 1 各向异性介质中各矢量的方向关系 Fig. 1 Directions of different vectors in anisotropic medium | |
虽然光波中同时具有E振动和H振动,但二者在光与物质的相互作用中所起作用却大不相同.如果把光与物质的相互作用看做是电磁场对物质中带电粒子的作用,电场力和磁场力分别为Fe=Eq,Fm=Bqv,且Fe/ Fm=c/v,当粒子的速度远小于光速时,电场力Fe要远远大于磁场力Fm,在光与物质的相互作用中通常电场起主要作用,所以电场矢量E通常也被称为光矢量.光的横波性决定了光矢量E位于与传播方向S垂直的平面内,而E在该平面内的具体振动方式称为光的偏振态.
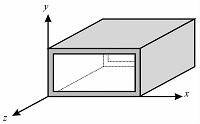
2 不同传导系统中偏振态的定义 2.1 波导系统这里所说的波导[1]都是指均匀波导系统,即在任一位置的波导横截面形状都是相同的.如图 2所示,波导系统平行于z轴,其横截面平行于xy面.波导系统中传输的电磁波可以分为TEM和非TEM波,电磁场仅在垂直于传输方向存在横向分量,而不存在纵向分量的波叫做TEM波;如果电磁场不但有横向分量,还有纵向分量,则对应的波称为非TEM波.微波传输或光通信中常用到的矩形波导、圆形波导、介质波导等结构中,如果磁场在波导横截面内,那么一定存在与磁力线铰链的位移电流,这样就必定存在纵向电场分量;同样,如果电场在横截面内,那么一定存在与电力线铰链的纵向磁场分量.所以这些波导结构中不会是TEM波.
|
Download:
|
| 图 2 矩形波导坐标示意图 Fig. 2 Coordinate system of rectangularwaveguide | |
沿波导传播的电磁波称为导行电磁波,导行电磁波在传播方向上一般是有E和H分量,可以用以下形式表示,
| $\left\{ \begin{matrix} E\left( x,y,z \right)={{E}_{0}}\left( x,y \right){{e}^{-i{{k}_{z}}z}}, \\ H\left( x,y,z \right)={{H}_{0}}\left( x,y \right){{e}^{-i{{k}_{z}}z}}. \\ \end{matrix} \right.$ |
式中,kz表示波的传播常数,E0(x,y)和H0(x,y)分别表示波导横截面上的电场和磁场,由于波导系统是均匀的,二者与z无关.在波导系统中,电磁场满足亥姆霍兹方程:
| $\left\{ \begin{matrix} \Delta {{~}^{2}}E+{{k}^{2}}E=0 \\ \Delta {{~}^{2}}H+{{k}^{2}}H=0 \\ \end{matrix} \right.,$ | (4) |
式中包含6个方向矢量Ez,Hx,Hy和Hz,Ex,Ey,且满足麦克斯韦方程组,但并不是完全独立的,对非TEM波只有Ez和Hz是相互独立的,所以只要求得2个纵向分量Ez和Hz,其他4个方向分量都可以由这2个矢量求导得出.
波导中导行波的TM/TE偏振态是根据电场或磁场是否仅存在横向分量来定义的.电磁波在波导中沿z轴纵向传播,当磁场H有z轴纵向分量,而电场E只存在xy平面内的横向分量时,称为TE波;当电场E有沿z轴纵向分量,而磁场H只存在xy平面内的横向分量时,称为TM波;当电场E和磁场H都有纵向分量时,则称为混合波.
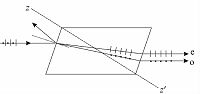
2.2 表面等离子体激元(SPP)在外界电磁场的作用下金属中的自由电子会相对金属中位置固定的正离子发生相对位移,产生电子密度的疏密分布,从而在金属和介质界面两边产生如图 3所示的电场.表面等离子体激元[3]是传播于介质与金属界面上的电磁激发,在金属与介质的界面处沿垂直于界面的方向呈指数衰减,在界面附近的局域约束场强最大. 假设表面等离子体波沿x方向传播,沿z方向指数分布,电磁波可以用下面表达式表示
| $\begin{align} & E(x,y,z)=Aexp(\pm {{k}_{z}}z)exp(i\beta x), \\ & H(x,y,z)=Aexp(\pm {{k}_{z}}z)exp(i\beta x), \\ \end{align}$ |
其中,β是波矢k的x分量,kz是波矢k的z分量,kz是正实数.在介质侧z>0,式中符号取“-”才能得到指数衰减;在介质侧z<0,符号取“+”才能得到指数衰减.将其代入旋度方程(1),由于∂x →iβ,∂y=0,∂z →±kz,∂t →-iω,化简后得到两套分别由(Hy,Ex,Ez)和(Ey,Hx,Hz)表示的方程组,它们是两组相互独立的解.
| $\left\{ \begin{matrix} \pm {{k}_{z}}{{E}_{x}}-i\beta {{E}_{z}}=i\omega {{\mu }_{0}}{{H}_{y}} \\ \pm {{k}_{z}}{{H}_{y}}=i\omega {{\varepsilon }_{0}}\varepsilon {{E}_{x}} \\ i\beta {{H}_{y}}=-i\omega {{\varepsilon }_{0}}\varepsilon {{E}_{z}} \\ \end{matrix} \right.,$ | (5) |
和
| $\left\{ \begin{matrix} \pm {{k}_{z}}{{H}_{x}}-i\beta {{H}_{z}}=i\omega {{\varepsilon }_{0}}\varepsilon {{E}_{y}} \\ \pm {{k}_{z}}{{E}_{y}}=-i\omega {{\mu }_{0}}{{H}_{x}} \\ i\beta {{E}_{y}}=i\omega {{\mu }_{0}}{{H}_{z}} \\ \end{matrix}. \right.$ | (6) |
与波导系统中对偏振态的定义方法一样,可以根据E和H是否仅存在横向分量判定是TE波还是TM波.因为表面等离子体谐振波沿x方向传播,在(Hy,Ex,Ez)组成的方程组中磁场H仅存在横向分量Hy,所以被称为TM波;(Ey,Hx,Hz) 组成的方程组中磁场E仅存在横向分量Ey,所以被称为TE波.

|
Download:
|
| 图 3 表面等离子体谐振的场分布 Fig. 3 Field of surface plasmon resonance | |
在介质与金属界面处,假设SPP以TM偏振波形式存在,分别用kzd和-kzm表示介质和金属中波矢的z方向分量,在方程组(5)的公式±kzHy=iωε0εEx中的“-”对应介质侧,“+”对应金属侧,根据边界条件Hyd=Hym,Exd=Exm,可以推得
| ${{k}_{zd}}{{k}_{zm}}=-{{\varepsilon }_{d}}{{\varepsilon }_{m}},$ | (7) |
由于在光频下金属的介电常数εm<0,而介质的介电常数εd>0,εm与εd为异号,所以式(7)成立,这说明SPP波可以以TM模式在金属/介质界面上存在.
同理,如果假设SPP在介质与金属界面上以TE偏振波存在,方程组(6)中存在公式±kzEy=-iωμ0Hx(“-”对应介质侧,“+”对应金属侧),根据边界条件Eyd=Eym,Hxd=Hxm,可以推得
| ${{E}_{y}}({{k}_{z}}d+{{k}_{z}}m)=0,$ | (8) |
由于介质和金属中z方向波矢分量的方向符号已代入运算方程,kzd和kzm都为正值,所以只有Eyd=Eym=0才能使公式(8)成立,这说明SPP波不能以TE偏振态存在.
可见SPP波只能以TM模式存在于金属/介质界面上.
2.3 各向同性介质中反射定律和折射定律设有两种各向同性的均匀透明介质,如空气和水,在二者组成的界面处,单色平面波从介质1向介质2入射,所满足的反射定律和折射定律[4]实际上是由两个遵循对称性的守恒定律组成的,即,频率ω守恒和边界波矢k||守恒(k||=|k|sinθ,其中|k|=nω/c).入射光、反射光、折射光和入射点处界面的法线被限制在同一个平面内,形成入射面.因为其传播方向限制在二维入射面内,通过解Maxwell方程也能得到两组相互独立的TE/TM偏振解.由于光波是横波,满足E×H=S,光矢量E为垂直于传播方向的横向矢量,所以相对于入射面,任意一个光矢量可以分解为垂直于入射面和平行于入射面的两个正交振动分量,振动方向垂直于入射面的称为s(senkrecht,德语,垂直)态分量,振动方向与入射面平行的称为p(parallel)态分量.当电矢量E为s态时,磁矢量H一定为p态,此时E仅作为横向分量出现,所以这样的波也被称为横向电偏振波,记为TE波;若H为s态,则E一定为p态,此时H仅作为横向分量出现,这样的波被称为横向磁偏振波,记为TM波.所以任一偏振态的入射光都可以看做是TM和TE波的叠加. 菲涅耳公式[3]也证明了反射波和透射波的s分量只与入射波的s分量有关,反射波和透射波的p分量只与入射波的p分量有关,s态和p态线偏振光是相互独立的.通过对光矢量的s/p态正交分解可以更方便地对光的传输特性进行分析,不但简化了运算过程,还提供了关于电磁场模式对称性的最直观信息.
与2.1和2.2节中的导行波和SPP波的传播行为相比较,它们对TM/TE偏振态的定义既相似又存在不同.三者都是在满足媒质特性和边界条件的情况下,通过解Maxwell方程得到的方程解来确定TM/TE偏振态的.不同点在于光波在两种各向同性透明介质界面处的反射和折射定律适用于大尺度界面的行为,属于几何光学范畴,传导的光波是TEM波.为简化分析过程,可将任一光矢量正交分解为s态和p态的叠加.而波导系统中的导行波和金属/介质界面上SPP波都是非TEM波.
2.4 各向异性晶体中的双折射原子或分子呈空间周期性排列的固体称为晶体,整体保持空间有序结构的晶体称为单晶体,一般单晶体都具有空间各向异性.当一束光由空气射入各向异性单轴晶体时,如图 4所示,通常情况下在晶体中会产生双折射现象[4].其中一束遵循折射定律的光称为o光,而另一束不遵循折射定律的光称为e光.
|
Download:
|
| 图 4 各向异性晶体中的双折射 Fig. 4 Birefringence in anisotropic crystal | |
通过检偏器观察,可以发现o光和e光都是线偏振光.借助惠更斯原理研究光在单轴晶体中的波面,o光波面为球面,意味着晶体中o光的传播规律与光在各项同性介质中的传播规律相同,沿各个方向的传播速度都相同.e光波面为旋转椭球面,意味着晶体中e光沿各方向的传播速度不同,o光和e光的传播速度仅在沿zz′光轴方向才相同.光线与晶体光轴构成的平面叫做主平面,包含晶体光轴并与晶体表面垂直的平面称为晶体的主截面.o光光矢量的偏振方向垂直于o光主平面,而e光光矢量的偏振方向在e光主平面内.而当入射光位于晶体的主截面内时,o光主平面和e光主平面均与晶体主截面重合,此时o光和e光的光矢量振动方向分别垂直和平行于入射面,根据前面介绍的光矢量(电矢量)的振动方向与入射面的相对关系,可以确定此时o光光矢量的偏振态为TE偏振或s态,e光光矢量的偏振态为TM偏振或p态,而通常情况下o光主平面和e光主平面位于不同平面,所以很难同时用s/p态或TM/TE偏振态对其偏振状态进行准确描述.一般利用晶体的双折射特性制成各种起偏器或检偏器等光学器件.
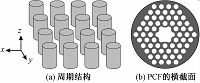
2.5 二维光子晶体假设二维光子晶体[2]的介电常数在xy平面内是具有周期性的,如图 5(a)所示,在与该平面垂直的轴向z→-z方向具有一致性和对称性.对任意kz=0的模式(波完全平行于xy平面传播),通过xy平面的反射总是保持不变,对应∂z=0,将其代入Maxwell方程组,化简后发现所有二维光子晶体中的传播模式都可以分为两种情况:一种情况是由(Ex,Ey,Hz)组成,电场仅限于xy平面内,磁场方向垂直于该平面;另一种情况是由(Hx,Hy,Ez)组成,磁场仅限xy平面内,而电场方向垂直于该平面.通过对两组方程分别求解得到各自能带结构的本征解,本征解对应频率的光可以在光子晶体中传播,没有本征解的频率范围则被称为禁带.
|
Download:
|
| 图 5 二维光子晶体 Fig. 5 2D photonic crystals:periodic structure (a) and cross-section of PCF (b) | |
早期对光子晶体的研究主要集中于光子晶体禁带的应用研究.光子晶体光纤(photonic crystal fiber,PCF)是一种基于二维光子晶体禁带的波导系统,图 5(b)给出光子晶体光纤横截面(xy平面)的示意图,纤芯为传导通路,纤芯周围为二维光子晶体周期结构,禁带频率的光波会被强烈束缚在纤芯沿z方向传播.与2.1节中的波导系统相同,研究者把电场E仅限于xy横截面内的(Ex,Ey,Hz)偏振模式的波称为TE波;把磁场H仅限xy横截面内的(Hx,Hy,Ez)偏振模式的波称为TM波.
随着对光子晶体传输特性的深入研究,人们发现频率位于导带内的波在光子能带的调制下可以产生如双折射[5]、负折射[6]和零折射[7]、超透镜[8]、超棱镜[9]等奇特的光学现象.在二维光子晶体中,当入射光波的传播方向平行于介质柱时,相当于光波在各向同性均匀介质中传播,没有受到任何调制;当光波的入射方向平行于二维光子晶体xy平面,光波受到二维周期性介质结构的调制表现出各种光学传输现象,传导波依然平行于xy平面,能够以光波的TM/TE偏振态进行分析.为保持光子晶体TM/TE偏振态定义的一致性,后来研究中仍然沿用光子晶体光纤中对TM/TE偏振态的定义,在二维光子晶体中就出现了当光波的E只存在垂直于传播方向的Ez横向分量时,称为TM波;当光波的H只存在垂直于传播方向的Hz横向分量时,称为TE波的现象.在空气和二维光子晶体或不同结构光子晶体的界面上同样满足频率ω不变和边界k||守恒条件,此时入射光、反射光、折射光和入射点法线都位于同一入射面中,该入射面平行于xy平面.根据光矢量(电矢量)的振动方向与入射面的相对关系,由于TE模式(Ex,Ey,Hz)对应的光矢量在xy入射面内振动,所以TE偏振模式也被称为p态;同样,由于TM (Hx,Hy,Ez)对应的光矢量振动方向垂直于xy入射面,所以TM偏振模态也被称为s态. 这里的s/p态不同于2.3节中光矢量的s/p态正交分量,而是分别对应着Maxwell方程的两组相互独立的本征解.
2.6 二维平板光子晶体实际应用中还存在一种具有有限高度的二维光子晶体[2],被称为二维平板光子晶体.该结构可以利用介质的折射率差在垂直方向上限制模场的泄露,通过适当设计,在二维平板光子晶体中引入线缺陷,可以得到光子晶体平板波导.二维情况下导行波模式也可以分为TE和TM两种模式,但对二维平板光子晶体来说,因为在垂直方向上缺少平移对称性,所以不存在纯粹的TE和TM模式.但根据其水平对称面的模场分布,可以将模式分为偶对称和奇对称模式,偶模式对应H(r)=H(-r)和E(r)=-E(-r);奇模式对应H(r)=-H(-r)和E(r)=E(-r).这种偶、奇对称模式与二维光子晶体情况下的TE和TM模式非常类似,所以二维平板光子晶体中的偶对称和奇对称模式又分别被称为TE和TM模式.
3 综合分析任意方向电磁波/光波在自由空间中传播时,满足Maxwell方程,由于本身为横波,所以统称为TEM波,不存在TE或TM的说法.但当这种均匀对称性被打破,方程解将产生简并态,例如电磁波被限制在xy平面内,在z方向是均匀不变的,系统是相对xy平面的镜面对称,z→-z的操作是对称的,可将∂z=0代入Maxwell方程,得到两组由6个场分量(Ex,Ey,Hz)和(Hx,Hy,Ez)组成的独立方程.Ez和Hz这2个分量相互独立,其他4个方向分量都可以用这2个分量求出,但两组方程之间又不存在旋转对称关系,所以可以得到两组不同的本征解,电场矢量可能的偏振方向要么沿z方向(TM),要么在xy平面内(TE).这就是为什么在二维电磁波/光波传输特性研究中要用TM/TE模式进行偏振描述的根本原因.
从几何光学和波动光学的观点出发,如果媒质的均匀性被打破会导致光的偏折.当由两种各项同性的透明介质组成的界面尺度足够大时,光的传播行为满足反射定律和折射定律,并且同时都满足频率ω不变和边界波矢k||守恒条件.当非均匀尺度较小时,可能会产生衍射或散射,在周期性介质结构的调制下满足布洛赫定律和波矢动量守恒,各方向的衍射或散射相互叠加,发生干涉相长或相消,从而得到禁带和导带,光波的传播路径发生改变.
为了进一步简化运算和便于分析模场的对称性,可以将任一光矢量进行正交分解,分解为垂直于入射面和平行于入射面的两个正交分量,分别对应s态和p态.由于光学中的光矢量对应的是电场矢量E,所以光矢量垂直于入射面的s态分量也被称为TE波,而光矢量在入射面内的p态分量被称为TM波,s态和p态偏振分量是互相独立的.由于电磁波/光波满足Maxwell方程,当电磁波/光波在二维对称系统中传播时,通过Maxwell方程推导可以得到两组相互独立的方程组,它们的本征解分别对应TM和TE偏振模式.可见利用TM/TE波对空间偏振态的描述超越了介质尺寸远大于光波长的几何光学领域中s态和p态,更具有概括性和普适性.
4 结论通过上述分析可以看出,无源区电磁波的TM和TE偏振态实质上是在∂z=0的二维条件下满足Maxwell方程的两组独立的方程解.对TM/TE偏振方向的定义通常沿用波导系统中对偏振态的定义:电场E只存在与传播方向垂直的横向分量的波,称为TE波;磁场H只存在与传播方向垂直的横向分量的波,称为TM波,该定义同样适用于光子晶体光纤.在二维光子晶体的光传输特性研究中,虽然传导光波在二维周期平面(xy)内传输,但TM/TE偏振态的定义仍沿用光子晶体光纤中的定义,所以在二维光子晶体中出现了TM/TE偏振方向与波导中导行波的偏振态定义矛盾的情况.通过理论推导可知在金属/介质界面上的SPP波只能以TM偏振态存在,证明TM/TE波只是Maxwell方程的两组独立的解,二者未必同时存在,该理论同样适用于几何光学和波动光学领域.遵循频率不变和边界守恒条件的反射光和折射光的光矢量相对入射面可以正交分解为s态和p态,在各向同性介质中光波的s态和p态分别对应TE和TM偏振态,使界面处光传播特性的研究更加清晰便捷.本文通过对不同传导系统中TE/TM偏振态的物理本质的比较和分析,成功解释了相关研究中遇到的一些困扰和疑问,有助于深入开展电磁波和电磁场的理论和实验研究.
| [1] | 冯恩信. 电磁场与电磁波[M]. 西安: 西安交通大学出版社, 2005 : 280 -299. |
| [2] | Joannopoulos J D, Johnson S G, Winn J N, et al. Photonic crystals: molding the flow of light[M]. Princeton: Princeton University Press, 2008 . |
| [3] | Maier S A. Plasmonics: fundamentals and applications[M]. New York: Springer, 2007 . |
| [4] | 蔡履中. 光学[M]. 北京: 科学出版社, 2007 . |
| [5] | Kang X L, Li G J, Li Y P. Positive-negative refraction effect based on overlapping bands in a two-dimensional photonic crystal[J]. J Opt Soc Am B , 2009, 26 :60–63. DOI:10.1364/JOSAB.26.000060 |
| [6] | Gaji R, Meisels R, Kuchar F, et al. All-angle left-handed negative refraction in Kagomé and honeycomb lattice photonic crystals[J]. Phys Rev B , 2006, 73 :165310. DOI:10.1103/PhysRevB.73.165310 |
| [7] | Dong G Y, Zhou J. Zero phase delay induced by wavefront modulation in photonic crystals[J]. Phys Rev B , 2013, 87 :125107. DOI:10.1103/PhysRevB.87.125107 |
| [8] | Parimi P V. Photonic crystals: imaging by flat lens using negative refraction[J]. Nature , 2003, 426 :404–405. DOI:10.1038/426404a |
| [9] | Kosaka H, Kawashima T, Tomita A, et al. Photonic crystals for micro lightwave circuits using wavelength-dependent angular beam steering[J]. Appl Phys Lett , 1999, 74 :1370. DOI:10.1063/1.123553 |
 2016, Vol. 33
2016, Vol. 33 


