Superconductor/ferromagnet(SC/FM) hybrid structures have been studied for long. In these systems, the competition between the ferromagnetism and superconductivity plays a crucial role. A wide range of phenomena, such as the 0-π transition[1], the odd-frequency pairing correlation[2], and the coexistence of ferromagnetism and superconductivity in one material[3-4], have been found. There have
been numerous studies on SC/FM/SC Josephson junctions, e.g., the spin-singlet SC/FM/spin-singlet SC junctions[5-6] and the spin-triplet-SC/FM/spin-triplet-SC junctions[7-9]. The Josephson effects in these junctions with unconventional superconductors are strongly influenced by the Andreev bound states[10] since they dominate the tunneling behavior at low temperature[11, 12].
In the spin-singlet-SC/spin-triplet-SC Josephsonjunctions[13-15], the lowest usual harmonic term (∝sinφ) in the current-phase relation, which originates from tunneling processes involving only a single Cooper pair, vanishes due to the opposite parity of the pairing states. In these junctions, the leading contribution to the junction current comes from the coherent tunneling of even numbers Cooper pairs, and therefore the sin2φ term is the leading harmonic[16-19].
However, in the Josephson junctions with ferromagnet inter layer, the spin singlet-triplet conversion will occur.Thus the lowest harmonic terms are expected[20]. The spin-triplet-SC/FM/spin-triple-SC junctions have been investigated extensively in the last decade[21]. It is found that the 0-π transition can be produced by tuning the orientation, changing the magnitude of magnetic moment, or varying the width of the ferromagnet layer. The spin-singlet-SC/FM/spin-triplet-SC junctions have been studied by several group[13, 22]. Recently, Brydon etal.[23]have discussed the conditions under which the single-Cooper-pair tunneling current ∝cosφ is possible. However, theoretical study on the 0-π transition in the spin-singlet-SC/FM/spin-triplet-SC junction is still lacking. In this work we will investigate how this single-Cooper-pair tunneling current is dependent on the strength of magnetization and the width of the central ferromagnet layer, an issue closely related to the investigation of 0-π transition in the spin-singlet-SC/FM/spin-triplet-SC junction. The Josephson current is calculated by using the Matsubara Green function formalism by Furusaki and Tsukada[24-26].
1 Model and formalismLet us consider a quasi two-dimensional double tunneling Josephson junction consisting of a clean ferromagnet layer with width L sandwiched between an s-wave SC (left) and a p-wave SC (right) as shown schematically in Fig. 1.

|
Download:
|
| Fig. 1 Schematic diagram of the s-wave SC/FM/p-wave SC Josephson junction | |
We adopt the Stoner model for central ferromagnet where the direction of magnetization (M)is specified by polar angle θ and azimuthal angle φ,
| $M=M(sin\theta cos\varphi , sin\theta sin\varphi , cos\theta ).$ | (1) |
The tunneling barriers located perpendicular to the x-axis are modeled by delta-type potentials V(x)=V1δ(x)+V2δ(x-L). The junction is described by the Bogoliubove-de Gennes (BdG) equation[27].The BdG equations in momentum space for quasiparticle states with energy E can be written as
| $\left( \begin{matrix} {{\widehat{h}}_{F}}\left( k \right) & 0 \\ 0 & -{{{\hat{h}}}^{T}}{{\left( -k \right)}_{F}} \\ \end{matrix} \right)\text{ }{{\Psi }_{F}}\left( k \right)=E{{\Psi }_{F}}(k)$ | (2) |
for ferromagnet, where
| $\left( \begin{matrix} \widehat{h}\left( k \right) & \hat{\Delta }\left( k \right) \\ \hat{\Delta }{{\left( k \right)}^{\dagger }} & -{{{\hat{h}}}^{T}}\left( -k \right) \\ \end{matrix} \right)\text{ }~{{\Psi }_{s, p}}\left( k \right)=E~{{\Psi }_{s, p}}(k)$ | (3) |
for superconductors, where
| $\hat{\Delta }\left( k \right)=~\left\{ \begin{matrix} i{{\Delta }_{s}}{{\sigma }_{2}}{{e}^{i}}{{\varphi }_{s}}, & s-wave, \\ i{{\Delta }_{p}}d\left( k \right)\cdot \hat{\sigma }{{{\hat{\sigma }}}_{2}}{{e}^{i}}{{\varphi }_{p}}, & p-wave. \\ \end{matrix} \right.$ | (4) |
In the above eguations
In this work we will confine ourselves to a case where the direction of the d vector is independent of wavevector k, namely d(k)=f(k)
| $f\left( k \right)=\left\{ \begin{matrix} {{k}_{x}}/{{k}_{F}}, \\ {{k}_{y}}/{{k}_{F}}, \\ \left( {{k}_{x}}+i{{k}_{y}} \right)/{{k}_{F}}, \\ \end{matrix} \right.\begin{matrix} {{p}_{x}}-wave, \\ {{p}_{y}}-wave, \\ \text{ }\left( {{p}_{x}}+i{{p}_{y}} \right)-wave. \\ \end{matrix}$ | (5) |
It is noted that the condition for the formation of zero-energy Andreev bound state(ZABS)[19] at the interface given by
| $f\left( {{k}_{x}},{{k}_{y}} \right)f\left( -{{k}_{x}},{{k}_{y}} \right)<0$ | (6) |
is satisfied for (px+ipy)-wave and px-wave states. In addition, for both the s-wave-SC/FM/(px+ipy)-wave-SC (s/FM/(px+ipy)) junction and the s/FM/px junctions the orbital pairing states of the superconductors have the same parity with respect to the interface momentum, and therefore a Josephson current with distinct phase relation J∝cosφ (φ=φs-φp) may appear especially when M‖d[23].
The wave function of our s/FM/p Josephson junction can be obtained by solving the BdG equation. We have
| $\begin{align} & \Psi \left( r \right)={{e}^{i{{k}_{y}}y}}[{{\Psi }_{s}}\left( x \right)\Theta \left( -x \right)+{{\Psi }_{F}}\left( x \right)\Theta \left( x \right)\Theta \left( L-x \right)+ \\ & {{\Psi }_{p}}\left( x \right)\Theta \left( x-L \right)], \\ \end{align}$ | (7) |
with
| $\begin{align} & {{\Psi }_{s}}\left( x \right)=\left( \begin{matrix} {{{\hat{u}}}^{e}}_{+} \\ {{{\hat{v}}}^{e}}_{+} \\ \end{matrix} \right){{e}^{i}}{{k}_{x}}x\hat{\alpha }+\left( \begin{matrix} {{{\hat{u}}}_{-}}^{h} \\ {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{v}}}_{-}}^{h} \\ \end{matrix} \right){{e}^{-}}i{{k}_{x}}x\hat{\beta }+ \\ & {{\left( \begin{matrix} {{{\hat{u}}}^{e}}_{\text{-}} \\ {{{\hat{v}}}^{e}}_{\text{-}} \\ \end{matrix} \right)}^{s}}{{e}^{^{-}i{{k}_{x}}x}}\hat{A}+{{\left( \begin{matrix} {{{\hat{u}}}_{+}}^{h} \\ {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{v}}}_{+}}^{h} \\ \end{matrix} \right)}^{s}}{{e}^{i{{k}_{x}}x}}\hat{B}, \\ & {{\Psi }_{p}}\left( x \right)={{\left( \begin{matrix} {{{\hat{u}}}^{e}}_{+} \\ {{{\hat{v}}}^{e}}_{+} \\ \end{matrix} \right)}^{p}}{{e}^{i}}{{p}_{x}}x\hat{C}+{{\left( \begin{matrix} {{{\hat{u}}}_{-}}^{h} \\ {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{v}}}_{-}}^{h} \\ \end{matrix} \right)}^{p}}{{e}^{-}}i{{p}_{x}}x\hat{D}, \\ & {{\Psi }_{F}}=\left( \begin{matrix} n\cdot \hat{\sigma } \\ 0 \\ \end{matrix} \right){{e}^{i{{{\hat{q}}}_{\sigma x}}x}}{{{\hat{e}}}_{l}}+\left( \begin{matrix} 0 \\ n\cdot {{{\hat{\sigma }}}^{*}} \\ \end{matrix} \right){{e}^{i{{{\hat{q}}}_{\sigma x}}x}}{{{\hat{f}}}_{l}}+ \\ & \left( \begin{matrix} n\cdot \hat{\sigma } \\ 0 \\ \end{matrix} \right){{e}^{-i{{{\hat{q}}}_{\sigma x}}x}}{{{\hat{g}}}_{l}}+\left( \begin{matrix} 0 \\ n\cdot {{{\hat{\sigma }}}^{*}} \\ \end{matrix} \right){{e}^{i{{{\hat{q}}}_{\sigma x}}x}}+{{{\hat{h}}}_{l}}, \\ \end{align}$ | (8) |
where
| $\psi _{\pm }^{e}=\left( \begin{matrix} \hat{u}_{\pm }^{e} \\ \hat{v}_{\pm }^{e} \\ \end{matrix} \right)=\left( \begin{matrix} {{u}_{\pm }}{{{\hat{\sigma }}}_{0}} \\ {{v}_{\pm }}\frac{\hat{\Delta }_{\pm }^{\dagger }}{\left| \hat{\Delta }_{\pm }^{\dagger } \right|} \\ \end{matrix} \right),$ | (9) |
| $\psi _{\pm }^{h}=\left( \begin{matrix} \hat{u}_{\pm }^{h} \\ \hat{v}_{\pm }^{h} \\ \end{matrix} \right)=\left( \begin{matrix} {{v}_{\pm }}\frac{{{{\hat{\Delta }}}_{\pm }}}{\left| {{{\hat{\Delta }}}_{\pm }} \right|} \\ {{u}_{\pm }}{{{\hat{\sigma }}}_{0}} \\ \end{matrix} \right),$ | (10) |
| ${{u}_{\pm }}=\sqrt{\frac{1}{2}\left\{ 1+\frac{\Omega \pm }{{{\omega }_{n}}} \right\}},{{v}_{\pm }}=\sqrt{\frac{1}{2}\left\{ 1-\frac{\Omega \pm }{{{\omega }_{n}}} \right\}},$ | (11) |
with
| $\begin{align} & {{\Omega }_{\pm }}=\sqrt{{{\omega }_{n}}^{2}+{{\left| {{{\hat{\Delta }}}_{\pm }}\left( k \right) \right|}^{2}}}, \\ & {{\omega }_{n}}=(2n+1)\pi {{k}_{B}}T, \\ & {{{\hat{\Delta }}}_{\pm }}\left( k \right)=\hat{\Delta }\left( \pm {{k}_{x}},{{k}_{y}} \right), \\ & {{{\hat{q}}}_{\sigma }}=\left( \begin{matrix} {{q}_{1}} & 0 \\ 0 & {{q}_{2}} \\ \end{matrix} \right). \\ \end{align}$ | (12) |
In the above expressions, the x-components of wavevectors for s-wave SC, p-wave SC, and FM are respectively given by
| $\begin{align} & {{k}_{x}}\approx {{k}_{F}}cos{{\theta }_{k}}, \\ & {{p}_{x}}\approx {{k}_{F}}cos{{\theta }_{s}}, \\ & {{q}_{1,2x}}\approx {{k}_{F}}\sqrt{1-\left( + \right)\eta }cos{{\theta }_{1,2}} \\ \end{align}$ | (13) |
with η=2m|M|/
| $sin{{\theta }_{k}}=\sqrt{1-\left( + \right)\eta }sin{{\theta }_{1,2}}=sin{{\theta }_{s}}.$ | (14) |
Therefore for injection angles
| ${{\theta }_{k}}>{{\theta }_{c}}=arccos\eta $ | (15) |
q1x is imaginary, and the wave for minority-spin quasiparticle decays exponentially into the ferromagnet region. There are two columns in our wave function and they represent the spin-up channel and spin-down channel, respectively. The coeffi-cients of incoming, reflecting, and outgoing waves
| $\begin{align} & \psi \left( x={{0}^{+}} \right)=\psi \left( x={{0}^{-}} \right), \\ & \psi \left( x={{L}^{+}} \right)=\psi \left( x={{L}^{-}} \right), \\ & \frac{d}{dx}\psi \left( x \right){{|}_{x=0+}}-\frac{d}{dx}\psi \left( x \right){{|}_{x=0-}}=2m{{V}_{1}}\psi \left( x=0 \right), \\ & \frac{d}{dx}\psi \left( x \right){{|}_{L=0+}}-\frac{d}{dx}\psi \left( x \right){{|}_{L=0-}}=2m{{V}_{2}}\psi \left( x=L \right). \\ \end{align}$ | (16) |
The Andreev reflection coefficients are defined by the off-diagonal elements of the matrix relation[28]
| $\left( \begin{matrix} {\hat{A}} \\ {\hat{B}} \\ \end{matrix} \right)=\left( \begin{matrix} {{{\hat{r}}}_{ee}} & {{{\hat{r}}}_{eh}} \\ {{{\hat{r}}}_{he}} & {{{\hat{r}}}_{hh}} \\ \end{matrix} \right)\left( \begin{matrix} {\hat{\alpha }} \\ {\hat{\beta }} \\ \end{matrix} \right).$ | (17) |
According to Green function method by Furusaki and Tsukada, the Josephson current can be expressed in terms of the Andreev coefficients
| $J\left( \varphi \right)=\frac{e}{2h}\sum\limits_{{{\omega }_{n}}}{T\sum\limits_{{{k}_{y}}}{\frac{1}{2{{\Omega }_{s}}}Tr[{{{\hat{\Delta }}}_{s}}{{{\hat{r}}}_{he}}-\hat{\Delta }_{s}^{\dagger }{{{\hat{r}}}_{eh}}]}}.$ | (18) |
When θ=0, the Andreev reflection coefficients can be calculated analytically, and we have
| ${{\hat r}_{eh}} = {e^{i{\varphi _s}}}\left( {\begin{array}{*{20}{c}} 0&{\frac{{{\xi _ - }}}{{{\Xi _ - }}}} \\ {\frac{{{\xi _ + }}}{{{\Xi _ + }}}}&0 \end{array}} \right),$ | (19) |
| ${{\hat r}_{eh}} = {e^{^ - i{\varphi _s}}}\left( {\begin{array}{*{20}{c}} 0&{\frac{{{{\tilde \xi }_ + }}}{{{\Xi _ + }}}} \\ {\frac{{{\xi _\_}}}{{{\Xi _\_}}}}&0 \end{array}} \right),$ | (20) |
where
| $\begin{gathered} {\Xi _ \pm } = 2i\tilde k{g_2}\left( {{u_p}^2{u_s}^2 - {{\tilde v}_p}^2{v_s}^2} \right) + 8i{{\tilde k}^2}{{\tilde q}_1}{{\tilde q}_2}{u_s}{v_s}{u_p}{{\tilde v}_p}sin\varphi \pm \hfill \\ [{\zeta _1}{\zeta _2}\left( {{u_p}^2 + {{\tilde v}_p}^2} \right)\left( {{u_s}^2 - {v_s}^2} \right) + 2{g_1}{{\tilde k}^2}\left( {{u_p}^2{u_s}^2 + {v_p}^2{v_s}^2} \right)] \hfill \\ {\xi _ \pm } = 2{g_1}{{\tilde k}^2}{u_s}{v_s}({u_p}^2 - {{\tilde v}_p}^2) \pm \hfill \\ [2i{g_2}\tilde k{u_s}{v_s}\left( {{u_p}^2 + {{\tilde v}_p}^2} \right) - 4{{\tilde k}^2}{{\tilde q}_1}{{\tilde q}_2}{u_p}{{\tilde v}_p}f], \hfill \\ {{\tilde \xi }_ \pm } = 2{g_1}{{\tilde k}^2}{u_s}{v_s}\left( {{u_p}^2 - {{\tilde v}_p}^2} \right) \pm \hfill \\ [2i{g_2}\tilde k{u_s}{v_s}\left( {{u_p}^2 + {{\tilde v}_p}^2} \right) - 4{{\tilde k}^2}{{\tilde q}_1}{{\tilde q}_2}{u_s}{v_s}{u_p}{{\tilde v}_p}{f^*}], \hfill \\ \end{gathered} $ | (21) |
with
| $\begin{align} & {{g}_{1}}=2{{{\tilde{q}}}_{1}}{{{\tilde{q}}}_{2}}cos({{q}_{1}}L)cos\left( {{q}_{2}}L \right)+ \\ & ({{{\tilde{q}}}_{1}}^{2}+{{{\tilde{q}}}_{2}}^{2})sin({{q}_{1}}L)sin\left( {{q}_{2}}L \right), \\ & {{g}_{2}}=\left( {{Z}^{2}}+{{{\tilde{k}}}^{2}} \right){{\chi }_{1}}+{{{\tilde{q}}}_{1}}{{{\tilde{q}}}_{2}}{{\chi }_{2}}+ \\ & Z({{{\tilde{q}}}_{1}}^{2}-{{{\tilde{q}}}_{2}}^{2})sin({{q}_{1}}L)sin\left( {{q}_{2}}L \right), \\ & {{\chi }_{1}}={{{\tilde{q}}}_{2}}sin({{q}_{2}}L)cos\left( {{q}_{1}}L \right)-{{{\tilde{q}}}_{1}}sin({{q}_{1}}L)cos\left( {{q}_{2}}L \right), \\ & {{\chi }_{2}}={{{\tilde{q}}}_{1}}sin({{q}_{2}}L)cos\left( {{q}_{1}}L \right)-{{{\tilde{q}}}_{2}}sin({{q}_{1}}L)cos\left( {{q}_{2}}L \right), \\ & f={{e}^{-i\varphi }}{{u}_{s}}^{2}-{{e}^{i\varphi }}{{v}_{s}}^{2},{{{\tilde{v}}}_{p}}={{v}_{p}}f\left( k \right), \\ & {{\zeta }_{\sigma }}=({{Z}^{2}}+{{{\tilde{k}}}^{2}}-{{{\tilde{q}}}^{2}}_{\sigma })sin\left( {{q}_{\sigma }}L \right)+2{{{\tilde{q}}}_{\sigma }}Zcos\left( {{q}_{\sigma }}L \right), \\ & {{{\tilde{q}}}_{\sigma }}={{q}_{\sigma }}/{{{\tilde{k}}}_{F}},k=k/{{k}_{F}},Z=2mV/{{k}_{F}}. \\ \end{align}$ | (22) |
The current J(φ) can in general be decomposed into a Fourier series,
| $I\left( \varphi \right)=\sum\limits_{n\ge 1}{[{{I}_{n}}sin\left( n\varphi \right)+{{J}_{n}}cos\left( n\varphi \right)]},$ | (23) |
where In and Jn are coefficient to be determined.The components with index n correspond to the amplitudes of the n th reflection processes of quasiparticles. The Jn vanishs if the time-reversal symmetry is not broken. In the following we consider a symmetric junction (V1=V2=V), and further assume Δs=Δp for simplicity.
It is well-known[29]that, in the spin space where the matrix in Eq. (2) is diagonal, the gap matrix in Eq. (3) for p-wave becomes
| ${{{\hat{\Delta }}}^{F}}_{p}\left( k \right)=\left( \begin{matrix} sin\theta & cos\theta \\ cos\theta & -sin\theta \\ \end{matrix} \right){{\Delta }_{p}}f(k){{e}^{i{{\varphi }_{p}}}},$ | (24) |
with
The Josephson current is normalized by the normal conductance of the junction at the limit η=0, J0=eπΔ0P/
| $P=\frac{1}{2}\sum\limits_{{{k}_{y}}}{\sum\limits_{\sigma =1,2}{\frac{4{{{\tilde{k}}}^{2}}{{{\tilde{q}}}^{2}}_{\sigma }}{{{\zeta }_{\sigma }}^{2}+4{{{\tilde{k}}}^{2}}{{{\tilde{q}}}^{2}}_{\sigma }}}}.$ | (25) |
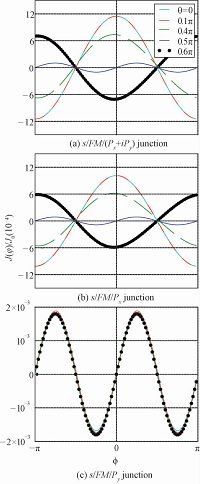
In this section we present results for the Josephson current in an s/FM/p junction. For the p-wave SC we choose the three different superconducting states listed in Eq. (5). We first discuss the dependence of current-phase relation on the polar angle θ. The parameters are fixed at T=0.01Tc, η=0.4, Z=5.0, and kFL=3.5. In Fig. 2(a) we plot the Josephson current as a function of φ for the s/FM/(px+ipy) junction with θ=0, 0.1π, 0.4π, 0.5π, and 0.6π. It is noted first of all that at φ=±π/2 the Josephson current vanishes in all the cases, implying the absence of the lowest usual sinusoidal term ∝sinφ. At θ=0 the current is dominated by the lowest unusual harmonic contribution ∝cosφ.J∝sin2φ at θ=π/2. In addition, detailed calculations show that J satisfies the relation J(φ, θ)=-J(-φ, π-θ). Therefore we can predict that the dominant term in the Josephson current for s/FM/(px+ipy) junction is
| $J\left( \varphi \right)={{{\tilde{J}}}_{1}}cos\theta cos\varphi +{{I}_{2}}sin\left( 2\varphi \right).$ | (26) |
Note that the contribution from the first term above vanishes identically when η=0.
|
Download:
|
| Fig. 2 Current-phase relation for s/FM/p Josephson junction | |
In Fig. 2(b) we show the results for s/FM/px junction.The results for this junction are very similar to those for the s/FM/(px+ipy) junction. Therefore the results can also be summarized by Eq. (26). We now analyge the results for s/FM/py junction, which are shown in Fig. 2(c).The term proportional to sinφ is absent in this case too. In contrast to the (px+ipy) and px cases the dominant contribution to Josephson current is ∝sin2φ. It is also noted that the current shows very weak dependence upon the angle θ and its amplitude is significantly reduced.
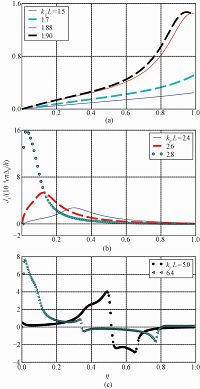
The results in Fig. 2 clearly indicate that the current-phase relation in a s/FM/p Josephson junction depends strongly on the detailed properties of p-wave Cooper pair wave function including both the spin and orbital parts. In particular, the unusual ∝cosφ term may appear when the spin is in the opposite-spin-pairing state, and simultaneously the orbital function f(k) has the same parity with respect to kx. At θ=π/2, the dominant contribution to Josephson current is ∝sin2φ for our three p-wave states. However, the amplitudes of the Josephson current in the px+ipy and px cases are largely enhanced in comparison to that in the py case (see Fig. 2), indicating the importance of resonant tunneling through the ZABS at low temperature (the low-temperature anomaly). These results are consistent with those obtained by Brydon et al.[23]in the calculation of a two-dimensional microscopic lattice model.We have discussed the current-phase relation for fixed values of η and kFL, where it is found in particular that single-Cooper-pair tunneling current (∝cosφ) is possible when certain conditions are fulfilled, e.g., M·d≠0. Next we will consider the s/FM/(px+ipy) junction and focus our attention to how the contribution from the cosφ term is affected by the magnitude of magnetization M.We explicitly calculate the η dependence of the coefficient J1 in Eq. (26). The coefficient J1 is approximately egual to the value of the total Josephson current at φ=0 and θ=0 (
Plotted in Fig. 3 are the η dependence of
|
Download:
|
|
Fig. 3 Coefficient |
|
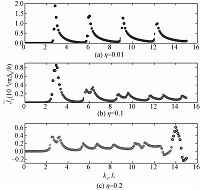
In our junction the quantum interference effect can arise due to the different wavevectors of quasiparticles within the ferromagnet, leading to an oscillatory variation of
|
Download:
|
|
Fig. 4 |
|
|
Download:
|
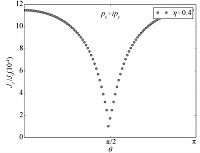
| Fig. 5 Critical Josephson current Jc as a function of θ for the s/F/(px+ipy) junction at η=0.4, Z=5.0, kFL=3.5, and T=0.01Tc | |
In this work, we have studied the Josephson effect in s/FM/p junction based on the BdG equation using the Matsubara Green function formalized by Furusaki and Tsukada. Three typical p-wave pairing states are considered for the sake of comparison. Our results concerning the contribution to Josephson current from the lowest harmonic term (∝cosφ) are consistent with the previous studies using the lattice model. We have further calculated the dependence of the cosφ term on the strength of magnetic moment as well as on the width of the ferromagnet layer. It is found, in particular, that the 0-π transition may occur in s/FM/(px+ipy) and s/FM/px junctions in certain range of system parameters. In addition, a possible spintronic application scheme has been discussed. Further systematic investigations about the dependence of the 0-π transition on parameters θ, η, kFL and Z and temperature T would be interesting.
| [1] | Ryazanov V V, Oboznov V A, Rusanov A Yu, et al. Coupling of two superconductors through a ferromagnet: evidence for a π junction[J]. Physical review letter , 2001, 86 :2427. DOI:10.1103/PhysRevLett.86.2427 |
| [2] | Begeret F S, Volkov A F, Efetov K B. Odd triplet superconductivity and related phenomena in superconductor-ferromagnet structures[J]. Reviews of Modern Physics , 2005, 77 :1321. DOI:10.1103/RevModPhys.77.1321 |
| [3] | Saxena S S, Agarwal P, Ahilan1K, et al. Superconductivity on the border of itinerant-electron ferromagnetism in UGe2[J]. Nature , 2000, 406 :587. DOI:10.1038/35020500 |
| [4] | Aoki D, Huxley A D, Ressouche E, et al. Coexistence of superconductivity and ferromagnetism in URhGe[J]. Nature , 2001, 413 :613. DOI:10.1038/35098048 |
| [5] | Buzdin A I, Bulaevskii L N, Panyukov S V. Critical-currenots cillations as a function of the exchange field and thickness of the ferromagnetic metal(F) in an S-F-S Josephson Junction[J]. JETP Lett , 1982, 35 :178. |
| [6] | Radovic Z, Lazarides N, Flytzanis N. Josephson effect in double-barrier superconductor-ferromagnet junctions[J]. Physical Review B , 2003, 68 :014501. |
| [7] | Kastening B, Morr D K, Manske D, et al. Novel Josephson Effect in Triplet-Superconductor-Ferromagnet-Triplet-Superconductor Junctions[J]. Physical review letter , 2006, 96 :047009. DOI:10.1103/PhysRevLett.96.047009 |
| [8] | Linder J, Grønsleth M S, Sudbø A. Tunneling currents in ferromagnetic systems with multiple broken symmetries[J]. Physical Review B , 2007, 75 :024508. DOI:10.1103/PhysRevB.75.024508 |
| [9] | Brydon P M R, Kastening B, Morr D K, et al. Interplay of ferromagnetism and triplet superconductivity in a Josephson junction[J]. Physical Review B , 2008, 77 :104504. DOI:10.1103/PhysRevB.77.104504 |
| [10] | Andreev A F. Thermal conductivity of the intermediate state of superconductors[J]. Sov Phys JETP , 1964, 19 :1228. |
| [11] | Tanaka Y, Kashiwaya S. Theory of the Josephson effect in d-wave superconductors[J]. Physical Review B , 1996, 53 :11957. DOI:10.1103/PhysRevB.53.R11957 |
| [12] | Barash Y, Burkhardt H, Rainer D. Low-temperature anomaly in the josephson critical current of junctions in d-wave superconductors[J]. Physical Review Letter , 1996, 77 :4070. DOI:10.1103/PhysRevLett.77.4070 |
| [13] | Kwon H J, Sengupta K, Yakovenko V M. Fractional ac Josephson effect in p-and d-wave superconductors[J]. European Physical Journal B , 2004, 37 :349. |
| [14] | Asano Y, Tanaka Y, Sigrist M, et al. Josephson interferometer in a ring topology as a proof of the symmetry of Sr2RuO4[J]. Physical Review B , 2006, 71 :214501. |
| [15] | Yokoyama T, Tanaka Y, Golubov A A. Theory of the Josephson effect in unconventional superconducting junctions with diffusive barriers[J]. Physical Review B , 2007, 75 :094514. DOI:10.1103/PhysRevB.75.094514 |
| [16] | Millis A, Rainer D, Sauls J A. Quasiclassical theory of superconductivity near magnetically active interfaces[J]. Physical Review B , 1988, 38 :4504. |
| [17] | Yip S. Weak link between conventional and unconve-ntional superconductors[J]. Journal of Low Temperature Physics , 1993, 91 :203. DOI:10.1007/BF00120849 |
| [18] | ] Sigrist M, Ueda K. Phenomenological theory of unconventional superconductivity[J]. Reviews of Modern Physics , 1991, 63 :239. DOI:10.1103/RevModPhys.63.239 |
| [19] | Asano Y, Tanaka Y, Sigrist M, et al. Josephson current in s-wave-superconductor/Sr2RuO4 junctions[J]. Physical Review B , 2003, 67 :184505. DOI:10.1103/PhysRevB.67.184505 |
| [20] | Eschrig M, Kopu J, Cuevas J C, et al. Theory of half-metal/superconductor heterostructures[J]. Physical Review Letter , 2003, 90 :137003. DOI:10.1103/PhysRevLett.90.137003 |
| [21] | Bujnowski B, Timm C, Brydon P M R. The Josephson effect between triplet superconductors through a finite ferromagnetic barrier[J]. J Phys: Condens Matter , 2012, 24 :045701. DOI:10.1088/0953-8984/24/4/045701 |
| [22] | Tanaka Y, Kashiwaya S. Josephson effect in unconventional-superconductor/ferromagnet/unconventional-superconductor junctions[J]. Journal of the Physical Society of Japan , 1999, 68 :3485. DOI:10.1143/JPSJ.68.3485 |
| [23] | Brydon P M R, Chen W, Asano Y, et al. Charge and spin supercurrents in triplet superconductor-ferromagnet-singlet superconductor Josephson junctions[J]. Physical Review B , 2013, 88 :054509. DOI:10.1103/PhysRevB.88.054509 |
| [24] | Furusaki A, Tsukada M. Dc Josephson effect and Andreev reflection[J]. Solid State Communications , 1991, 78 :299. DOI:10.1016/0038-1098(91)90201-6 |
| [25] | Asano Y. Direct-current Josephson effect in SNS junctions of anisotropic superconductors[J]. Physical Review B , 2001, 64 :224515. DOI:10.1103/PhysRevB.64.224515 |
| [26] | Brydon P R. Spontaneous spin current due to triplet superconductor-ferromagnet interfaces[J]. Physical Review B , 2009, 80 :224520. DOI:10.1103/PhysRevB.80.224520 |
| [27] | de Gennes P G. Superconductivity of metals and alloys[M]. New York: Addison-Wesley, 1989 : 137 -145. |
| [28] | Asano Y. Josephson spin current in triplet superconductor junctions[J]. Physical Review B , 2006, 74 :220501. DOI:10.1103/PhysRevB.74.220501 |
| [29] | Yinhan Z, Qiang C, Biao J. Tunneling conductance in ferromagnet/Sr2RuO4 junction: Detection of the d-vector direction[J]. Physica C , 2010, 470 :502. DOI:10.1016/j.physc.2010.04.008 |
| [30] | Mackenzie A P, Maeno Y. The superconductivity of Sr2RuO4 and the physics of spin-triplet pairing[J]. Reviews of Modern Physics , 2003, 75 :657. DOI:10.1103/RevModPhys.75.657 |
 2016, Vol. 33
2016, Vol. 33 


