The Volterra integral equation of the second kind is a special type of integral equations and is often evolved in many engineering domains such as petrol industry. Many methods have been established for solving this kind of equation. Yusufoglu^[1-2] solved systems of the integral equations using the homotopy perturbation and the Lagrange method. Huang et al.^[3] used the Taylor expansion method and obtained an approximate solution. Yang^[4] used the Chebyshev polynomials method to solve the equation,while Yousefi^[5] presented a numerical method for the Abel integral equation by Legendre wavelets. Khodabin et al.^[6] numerically gained the solution of the stochastic Volterra integral equations using triangular functions and their operational matrix of integration. Kamyad et al.^[7] proposed an algorithm based on the calculus of variations and discretization method to solve linear and nonlinear Volterra integral equations. The domain de-composition ^[8-10] was proposed for obtaining the approximate analytic solution of the integral equation.

The integral equation involved in this paper stems from the description of pressure distribution in oil and gas development,and it is given in Eq.(1),

$u\left( t \right)=g\left( t \right)+\int\limits_{0}^{t}{K\left( t-\tau \right)}F\left[ u\left( \tau \right) \right]d\tau ,$

(1)

where the source function g(t) is given and the kernel function K(t) and function F(u) are known to be continuous functions. Function u(t) needs to be determined.

Since the function g(t) is not necessarily zero,this kind of integral equations are generally regarded as non-homogeneous equations. In addition,the transformation of the unknown function by F-function increases the nonlinear degree of the problem. The difficulty in solving this kind of equation numerically is to discrete the integral upper limit and the integral expression synchronously.

1 Discretization of the integral equation

It is obvious in Eq.(1) that,when t=0，u(0) is equal to zero. Based on this fact,a method is proposed by converting the original equation into ordinary differential equation with initial value by derivation and then solving the differential equation. The derivation of the original equation is expressed in Eq.(2),

$\frac{du}{dt}=\frac{dg}{dt}+\frac{d}{dt}\int\limits_{0}^{t}{K\left( t-\tau \right)}F\left[ u\left( \tau \right) \right]d\tau .$

(2)

Practice shows that there is no explicit derivation for this kind of equation,in which convolution is invo-lved. So,the way to the solution goes as following.

If we define that t_i=iΔt (i=0,1,2,…,N) and f(t_i)=f(iΔt)=f_i， we can express the discretization of Eq.(1) in Eq.(4)

$u\left( t \right)=g\left( t \right)+\int\limits_{0}^{t}{K\left( t-\tau \right)}F\left[ u\left( \tau \right) \right]d\tau ,$

(3)

${{u}_{i}}={{g}_{i}}+\int\limits_{0}^{t}{K\left( {{t}_{i}}-\tau \right)}F\left[ u\left( \tau \right) \right]d\tau .$

(4)

And then new designation is defined as

${{\varphi }^{i}}\left( \tau \right)=K\left( {{t}_{i}}-\tau \right)F\left[ u\left( \tau \right) \right],$

(5)

${{Q}_{i}}=\int\limits_{0}^{{{t}_{i}}}{{{\varphi }^{i}}\left( \tau \right)}d\tau ,$

(6)

$u\left( {{t}_{i}} \right)=g\left( {{t}_{i}} \right)+Q\left( {{t}_{i}} \right)$

(7)

where Q_i can be expanded with composite integral formula. Different expansion approaches can be used to get the desirable accuracy. In this paper,composite trapezoidal formula is used. So,Q_i can be expanded as following

$\begin{align} &{{Q}_{i}}\approx \Delta t\sum\limits_{k=0}^{i-1}{\frac{{{\varphi }^{i}}\left( {{t}_{k}} \right)+{{\varphi }^{i}}\left( {{t}_{k+1}} \right)}{2}} \\ &=\Delta t\left( \frac{{{\varphi }^{i}}\left( {{t}_{0}} \right)+{{\varphi }^{i}}\left( {{t}_{i}} \right)}{2}+\sum\limits_{k=0}^{i-1}{{{\varphi }^{i}}\left( {{t}_{k}} \right)} \right). \\ \end{align}$

(8)

Defining

$\varphi _{k}^{i}={{\varphi }^{i}}\left( {{t}_{k}} \right)=K\left( {{t}_{i}}-{{t}_{k}} \right)F\left[ {{u}_{k}} \right]$

(9)

and substituting Eq.(8) into Eq.(7),we get

${{u}_{i}}={{g}_{i}}+{{Q}_{i}}={{g}_{i}}+\Delta t\left( \frac{\varphi _{0}^{i}+\varphi _{i}^{i}}{2}+\sum\limits_{k=1}^{i-1}{\varphi _{k}^{i}} \right).$

(10)

Defining

${{P}_{i}}={{u}_{i}}-\Delta t\frac{\varphi _{i}^{i}}{2}={{u}_{i}}-\Delta t\frac{F\left( 0 \right)F\left( {{u}_{i}} \right)}{2}$

(11)

and substituting Eq.(10) into Eq.(11),we get

${{P}_{i}}={{g}_{i}}+\Delta t\left( \frac{F\left( {{t}_{i}} \right)F\left( {{u}_{0}} \right)}{2}+\sum\limits_{k=1}^{i-1}{K\left( {{t}_{i}}-{{t}_{k}} \right)F\left[ {{u}_{k}} \right]} \right)$

(12)

Since g-function and k-function are known,we can determine the value of P_i using Eq.(12) if new designation U_i-1=[u₀,u₁,…,u_i-1] is known. Then we substitute the known P_i into Eq.(11) to solve the value of u_i.

2 Algorithm and convergence analysis

Based on the discretization mentioned above,the specific iteration procedure is as following.

When i=0， then,Q₀=0，u₀=g₀.

When i=1， according to Eq.(10),we have

${{P}_{1}}={{g}_{1}}+\Delta t\frac{K\left( {{t}_{1}} \right)F\left( {{u}_{0}} \right)}{2}$

(13)

Introducing P₁ into Eq.(13),the value of u₁ can be obtained by using the following equation:

${{P}_{1}}={{u}_{1}}-\Delta t\frac{K\left( 0 \right)F\left( {{u}_{1}} \right)}{2}$

(14)

When i=2， by introducing U₁=[u₀,u₁] into Eq.(12),we obtain

${{P}_{2}}={{g}_{2}}+\Delta t\left( \frac{K\left( {{t}_{2}} \right)F\left( {{u}_{0}} \right)}{2}+K\left( {{t}_{2}}-{{t}_{1}} \right)F\left[ {{u}_{1}} \right] \right).$

(15)

And then substituting P₂ into Eq.(11),we get

${{P}_{2}}={{u}_{2}}-\Delta t\frac{K\left( 0 \right)F\left( {{u}_{2}} \right)}{2}.$

(16)

Solving the above equation,we get the value of u₂， which means that U₂=[u₀,u₁,u₂] is available.

When i=n， substituting U_n-1=[u₀,u₁,…,u_n-1] into Eq.(12),we obtain

$\begin{align} &{{P}_{n}}={{g}_{n}}+\Delta t \\ &\left( \frac{K\left( {{t}_{n}} \right)F\left( {{u}_{0}} \right)}{2}+\sum\limits_{k=0}^{i-1}{K\left( {{t}_{n}}-{{t}_{k}} \right)}F\left[ {{u}_{k}} \right] \right) \\ \end{align}$

(17)

Then we get the following equation by introducing P_n into Eq.(11),and we get the expression of P_n,

${{P}_{n}}={{u}_{n}}-\Delta t\frac{K\left( 0 \right)F\left( {{u}_{n}} \right)}{2}.$

(18)

Solving the above equation,we get the value of u_n， which means that U_n=[u₀,u₁,u₂,…,u_n] is available.

The error in this numerical solution rises from the numerical integration in Eq.(8) and the accumulation of error in Eq.(12). The kernel function and F-function are continuous in the solving interval [a,b]. If the second-order derivatives of φ(x) are continuous in the same interval,we can express the truncation error of composite trapezoidal formula in Eq.(9):

${{R}_{N}}\left( \varphi \right)=-\frac{b-a}{12}\Delta {{t}^{2}}\varphi ''\left( \varepsilon \right),a<\varepsilon <b$

(19)

For the above equation,it is obvious that the error has the order of Δt².

It is proved that the accumulation of error is decided by the F-function as follows:

Define the error of u at step N as e_N， and Pe(t_N) as the error of P at the same step. We have

${{e}_{N}}=u\left( {{t}_{N}} \right)-\left( {{u}_{N}} \right)={{e}_{N}}\left( {{R}_{N}}\left( \varphi \right) \right).$

(20)

According to Eq.(12),Pe(t_N) can be expressed as follows:

${{P}_{e}}\left( {{t}_{N}} \right)=\Delta t\sum\limits_{k=1}^{N-1}{K\left( {{t}_{N}}-{{t}_{k}} \right)}F\left[ {{e}_{k}} \right].$

(21)

Since the kernel function and F-function are continuous in interval [a,b]， it is reasonable to assuming that (t_N-t_k)F[e_N]<PR_N. Assuming that the error increases,We have

$P{{e}_{N}}<\Delta t\left( N-1 \right)P{{R}_{N-1}}<\left( b-a \right)P{{R}_{N-1}}.$

(22)

According to Eq.(11),we have

${{e}_{N+1}}=F\left( P{{e}_{N}} \right)<F\left[ \left( b-a \right)P{{R}_{N-1}} \right].$

(23)

In the case that F-function is desirable,the following relationship can be met,

${{e}_{N+1}}<{{e}_{N}}$

(24)

So,the convergence of the problem relies on property of F-function.

3 Case studies

Case 1

To verify the feasibility and accuracy of the proposed method,case studies are given. The related known functions are listed as follows:

$u\left( t \right)=-\frac{1}{2}+\frac{1}{2}{{e}^{2x}}+\int\limits_{0}^{t}{-}{{e}^{2\left( -\tau \right)}}u{{\left( \tau \right)}^{2}}d\tau ,$

(25)

$K\left( x \right)=-{{e}^{2x}},$

(26)

$g\left( x \right)=-\frac{1}{2}+\frac{1}{2}{{e}^{2x}},$

(27)

$F\left( u \right)={{u}^{2}}$

(28)

It is known that the numerical solution of this particular problem is:

$u\left( t \right)=-1+\sqrt{2}\tanh \left( \sqrt{2t}+\frac{1}{2}\log \frac{\sqrt{2}-1}{\sqrt{2}+1} \right).$

(29)

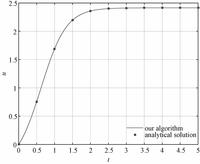
Figure 1 shows the difference between the numerical solution and the analytical solution. The red line indicates the solution of our algorithm and the blue points stand for the analytical solution. In the numerical solution,Δt=0.01 is applied,which means that the solution has an accuracy of 4th order.

The errors for the specific points are given in Table 1. The accuracy of the numerical solution is high enough and meets engineering computation needs.

Case 2

The second case is as follows:

$u\left( t \right)=t+\int\limits_{0}^{t}{\left. \left( 2u\left( \tau \right)-\sin u\left( \tau \right) \right) \right)}d\tau ,$

(30)

K(x)，g(x)，F(u) are as follows:

$K\left( x \right)=1$

(31)

$g\left( x \right)=t$

(32)

$F\left( u \right)=2u-\sin u.$

(33)

It can be transferred into a nonstiff differential equation

$\frac{du}{dt}=1+2u-\sin \left( u \right),u\left( 0 \right)=0.$

(34)

The above differential equation could be solved by using Runge-Kutta algorithm.

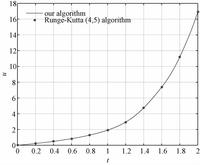
Figure 2 shows the difference between our algorithm and the Runge-Kutta algorithm. The red line indicates the solution of our algorithm and the blue points stand for Runge-Kutta algorithm.

The errors for the specific points are given in Table 2. The results of our algorithm are in close proximity to the results of Runge-Kutta algorithm.

4 Conclusion

A new numerical solution is proposed and verified for the Volterra integral equation of the second kind. The established method would work with higher precision it one chooses a higher-precision numerical integration method. The proposed solution in this paper is easy to program and calculate, and the relative errors for the study cases are small enough. The limitation of the method is its dependence on the property of F-function.