曲线是计算机辅助几何设计(CAGD)中的基本研究对象之一,曲线的研究包括表示形式分析、几何特性分析、曲线逼近和求交分析等[1-3].在曲线逼近的研究方法中,一个重要的方法是细分方法.细分方法是基于网格细化的离散表示方法,它可以从任意拓扑网格构造光滑曲线/曲面[1].其基本思想是:对给定的初始控制点及其拓扑关系,定义一个细分规则,在给定的初始网格中插入新的顶点,从而不断细化产生一个新的网格序列.理论上,在细分极限时,该网格序列收敛于一条光滑曲线或者一张光滑曲面[4-6].
Bézier形式是CAGD中的经典表示形式,它赋予控制系数以明确的几何意义,并且还有其他便于造型设计的良好性质,例如凸包性、变差缩减性[1-2, 5]等,因而也是曲线、曲面表示的常用形式[7-8].平面Bézier曲线的分段线性逼近可以通过著名的de Casteljau算法实现.de Casteljau算法属于细分方法,人们常以0.5为参数细分点[5-6],我们称之为定参数方法.本文将考虑如何更好地选择细分参数,从而得到效率更高的细分算法.曲线细分的本质是寻找一种线性逼近,即若干次细分后,每一段曲线已经接近直线段,从而可以用折线段代替原曲线.因此细分过程中,需要优化细分参数,使得折线段可以快速逼近真实的曲线.根据平面Bézier曲线的包围盒性质,可通过要求细分曲线段包围盒面积最小或者尽量扁平来实现细分优化,本文将讨论这两种优化条件下的细分算法.
对于2次平面Bézier曲线而言,当细分参数为0.5时,获得的细分控制多边形的面积是最小的.3次及以上的一般平面Bézier曲线无此结果,细分包围盒扁平度也不在参数0.5时达到最小.因此对于高次数形状复杂的平面Bézier曲线,需要分别根据优化条件计算细分参数.通过选择合适的参数,使得得到的细分曲线的凸包[3]面积最小或者控制多边形最扁平,从而很好地贴近Bézier曲线,以达到折线逼近曲线的效果.准确优化细分参数的求解需要一定计算量,我们根据算例结果给出了合理的数值遍历方法.根据细分若干次以后参数变化区域缩小的实际情况,只在算法的前N步中计算最优参数.最终的数值化算法在效率上高于 de Casteljau定参数算法.
1 基础知识我们称n次多项式
定义1.1 给定n+1个向量Pi∈R2,其中i=0,1,…,n.我们称
我们不加证明地给出本文相关的平面 Bézier曲线性质.
性质1.1[2, 5] Ⅰ(几何不变性)平面Bézier曲线的位置和形状只与特征多边形顶点的位置有关,它不依赖于坐标系的选择.
Ⅱ(凸包性)平面Bézier曲线P(t),t∈[0,1,]总落在其控制点Pi构成的凸包中.
Ⅲ(变差缩减性质)对于平面曲线,任意直线和Bézier曲线的交点个数不多于该直线与控制多边形交点数.
若给定参数值t*∈[0,1],可以通过代入计算得到曲线上一点P(t*).也可以直接用控制点计算得到P(t*),即由de Casteljau算法求出所定义的平面Bézier曲线上的一点P(t*).
Bézier曲线的de Casteljau算法公式[5]
| $\left\{ \begin{align} & P_{i}^{0}\left( {{t}^{*}} \right)\equiv P_{i}^{0}={{P}_{i}},i=0,\cdot \cdot \cdot ,n. \\ & P_{i}^{r}\left( {{t}^{*}} \right)=\left( 1-{{t}^{*}} \right)P_{i}^{r-1}\left( {{t}^{*}} \right)+{{t}^{*}}P_{i+1}^{r-1}\left( {{t}^{*}} \right) \\ \end{align} \right.$ | (1) |
其中,r=1,…,n,i=0,…,n-r.由de Casteljau算法求出所定义的Bézier曲线上的一点P(t*),同时该点把曲线分为2个n次的子曲线段:P(t),t∈[0,t*]和P(t),t∈[t*,1],即de Casteljau算法给出了Bézier曲线的一个分割(细分).2个细分曲线段Pl(t)和Pr(t)所对应的新Bézier控制顶点分别为P00,P10(t*),…,Pn0(t*)和Pn0(t*),Pn-11(t*),…,P0n,这2组控制顶点给出了2个子曲线段分别在各自局部参数域[0,1,]上的Bézier表示.
应用de Casteljau算法进行细分,人们一般固定细分参数t=0.5,本文称之为定参数算法(定参法).细分过程是对曲线在t=0.5处进行细分,并且对细分曲线重复该过程,依次进行下去,在进行k次细分后以2k个平面Bézier多边形结束,每一个多边形描述原来曲线的一小段.如果k取值足够大,这些小曲线段将近乎于直线段,根据凸包性,此时可以用控制多边形逼近原曲线.下面采用2种方式选择细分参数,使得细分后的曲线段能够更加快速地被直线段逼近.
2 细分参数选取首先我们考虑细分曲线的凸包面积最小条件下对应的参数,定义如下.
定义2.1 记平面Bézier曲线P(t)的凸包面积为Area(P(t)),则对给定曲线P(t),其凸包最优参数定义为t*=arg(mint(Area(Pl(t))+Area(Pr(t))).
性质2.1 二次平面Bézier曲线的凸包最优参数t*=0.5.
证明 根据Bézier曲线几何不变性和仿射变换,可设二次Bézier曲线的控制点为(-1,0),(0,1),(a,b),不妨设b>0.则细分后2个控制多边形的凸包面积分别为S1=bt3,S2=b(1-t)3则细分后2个凸包面积和为S=S1+S2=b(3t2-3t+1),在t*=0.5处取得最小值,故最优参数t*=0.5. □
对于3次以上的平面Bézier曲线,其凸包最优参数不再固定为0.5.需要更多限制条件才有相应结果.称n次平面Bézier曲线P(t)是轴对称,如果其控制点Pi和Pn-i,i=0,…,n关于P0Pn的中垂线对称.
性质2.2 设P(t)是具有凸控制多边形的轴对称平面Bézier曲线,则t*=0.5是细分凸包面积和函数的极值点;进一步若细分凸包面积函数在(0,1)上是凸的,则t*=0.5是凸包最优参数.
证明 根据Bézier曲线的变差缩减性,具有凸控制多边形的Bézier曲线为凸曲线,则对于细分曲线Pl(t)和Pr(t),f(t)=Area(Pl(t))和g(t)= Area(Pr(t))在t∈[0,1,]上分别是单调增加和单调减少的.控制多边形是凸的,则f(t)+g(t)在边界点t=0或1处取极大值.又根据曲线对称性和Bézier表示的参数对称性,有g(t)=f(1-t),则f(t)+g(t)=f(t)+f(1-t).考虑其一阶导数的(f(t)+f(1-t))′=f′(t)-f′(1-t),可以发现t*=0.5是一极值点.
进一步,若f(t)为凸函数,则f(t)+f(1-t)在(0,1)上无其他极值点,否则有t0∈(0,1)使得f′(t0)=f′(1-t0),与f(t)在(0,1)上为凸矛盾,t*=0.5不是极大值点,因此只能为最小值点,即凸包最优参数. □
3次以上一般曲线凸包最优参数值不再是固定值,而上述性质在曲线一次细分之后不能再保持,因此一般复杂曲线的凸包最优参数需要计算得到.给定足够小的ε,当Area(P(t))<ε时,则认为凸包足够小,可以用控制多边形逼近原曲线段.
其次,我们考虑另一优化参数条件,使得细分曲线控制多边形尽量扁平.
定义2.2 设Pi(i=0,1,…,n)为平面Bézier曲线P(t)的控制多边形顶点,D(P0Pn,Pi)是Pi到P0Pn的距离,记
性质2.3 对称二次平面Bézier曲线的扁平度最优参数t*=0.5.
证明 设二次Bézier曲线的控制点为P0=(-1,0),P1=(0,a),P2=(1,0),不妨设a≥0,令细分参数为t,则得到2个子曲线Pl(t),Pr(t)对应的控制多边形,根据定义2.2,我们得到只要求解以下问题的最小值点即可:
| $\begin{align} & Dis\left( t \right)=Dis\left( {{P}^{l}}\left( t \right) \right)+Dis\left( {{P}^{r}}\left( t \right) \right) \\ & =\frac{a{{t}^{2}}}{\sqrt{{{\left( a-at \right)}^{2}}+1}}+\frac{a{{\left( t-1 \right)}^{2}}}{\sqrt{{{a}^{2}}{{t}^{2}}+1}}, \\ \end{align}$ | (2) |
其中,0≤t≤1,并且a≥0.经计算Dis(t)在t*=0.5取极值,又
一般平面曲线都不具有固定的扁平度最优参数,需要计算得到.若给定足够小的ε,当Dis(P(t))<ε时,我们认为控制多边形足够扁平,可以用控制多边形逼近原曲线段.
根据上述定义,当细分过程中某子细分曲线有Area(P(t))<ε(或Dis(P(t))<ε),停止该细分曲线的进一步细分,用控制多边形作为该部分曲线的近似.当所有的细分曲线段都停止细分,就得到了原Bézier曲线的一个近似折线段逼近.下面分别给出凸包最优参数和扁平度最优参数的算法描述.
凸包最优参数算法(凸包法):
输入:Pi(i=0,…,n)为给定的一条平面Bézier曲线的控制多边形顶点.
输出:凸包最优细分参数t0.
1) 假定t为细分参数,根据de Casteljau算法,得到其2个子控制多边形T1,T2的顶点,它们均为关于t的参数;
2) 设T1的顶点为Vi(i=0,…,n),计算出顶点集T1的凸包的面积Area1,同样求出T2对应的凸包面积Area2,考虑令Area(t)=Area1+Area2,它是t的函数,求t0(0<t0<1)为Area(t)最小值点.
扁平度最优参数算法(扁平法):
输入:Pi(i=0,…,n)为给定的一条平面Bézier曲线的控制多边形顶点.
输出:扁平度最优细分参数t0.
1) 假定t为细分参数,根据de Casteljau算法,得到其2个子控制多边形T1,T2的顶点,它们均为关于t的参数;
2) 设T1的顶点为Vi(i=0,…,n),计算出顶点Vi(i=1,…,n-1)到V0Vn的几何距离为d1i,求
上述算法理论上都有准确解,但是求准确解需要进行符号求解高次多项式的根,运算量较大,因而我们对算法进行了数值化改进.根据大量算例测试,最优参数几乎都落在区间t∈[0.2,0,8]之中,因此我们用数值遍历选择最优参数,即通过遍历t=0.2+0.05·k(k=0,1,…,12),寻找凸包最优参数或扁平度最优参数.而经过若干次细分后,这里设为N次,再往后的细分参数基本在0.5附近.实际上,经过N次细分后,曲线段已经较短且基本都是单弧形,而我们知道单个弧形曲线是可以用二次曲线逼近的,而根据性质2.1和2.3,t*=0.5是二次曲线的最优参数合理选择,因此N步以后我们不用再做参数优化选取,直接取0.5即可.
数值化算法得到的细分参数不一定是严格的最优参数,但是速度有极大提高,而且与定参数方法相比,尤其对于高次复杂平面Bézier曲线的细分,我们的算法有效率优势.
3 实例及算法分析我们针对不同的高次复杂平面Bézier曲线分别使用定参数方法、凸包最优参数及扁平度最优参数算法进行了算例检验.实验测试平台为配备Intel Core i3处理器及4 G内存的HP431笔记本电脑,测试软件为Matlab R2014a.
首先给定精度ε以及算法终止条件,进行曲线逼近算法比较.由于Bézier细分算法本身具有良好的效果,精度很小就可以很好地逼近,在本文中,取ε=1×10-5,实验结果表明在此精度下优良的拟合效果得到足够保证.为了做同精度下的算法效率比较,对于由{P*i}i=0,…,n定义的细分曲线我们设定了统一的精度终止条件:
| $\frac{\underset{i\in \left\{ 1,\cdot \cdot \cdot ,n-1 \right\}}{\mathop{\max }}\,\left( D\left( {{P}_{0}}^{*}{{P}_{n}}^{*},{{P}_{i}}^{*} \right) \right)}{\max \left( {{y}_{\max }}-{{y}_{\min }},{{x}_{\max }}-{{x}_{\min }} \right)}\le \varepsilon .$ | (3) |
其中,xmax=max{xi|Pi=(xi,yi),i=0,1,…,n}为原始曲线最右控制点对应的横坐标值,xmin,ymax,ymin定义类似,该分母的选取是为精度误差不受仿射变换影响.
其次设定算法效率比较的标准,我们采用比较算法提高率来进行判断.提高率是指计算时间提高率:
提高率=(定参数运算时间-改进算法运算时间)/定参数运算时间.
这里的改进算法运算时间包括参数选取和曲线细分两部分的计算时间.最后通过算例演绎算法差异.Bézier曲线随次数不断增高,曲线复杂度不断增大.我们选取次数逐渐增大的一组平面Bézier曲线作为算例.由于曲线次数较低时,算法迭代次数也相应较少,2种改进算法在前N次遍历寻找最优参数中所花费的时间是固定参数法的倍数级,占用较多时间,使得效率没有明显提高,这里我们舍弃低次Bézier曲线.
我们用交互输入方法随机点画了10条次数从12不断提高的平面Bézier曲线,测试定参数方法和2种改进算法的运算速度.
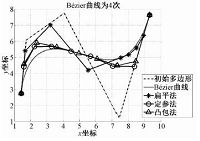
图 1给出Bézier曲线及其控制多边形细分比较,分别利用定参数方法和2种改进算法进行了一次细分.
|
Download:
|
| 图 1 不同细分算法细分一次的比较结果 Fig. 1 Comparative results of different algorithms after the first subdivision | |
提高曲线次数获得更高的复杂性(参数选取固定N=3),表 1列出3种方法的运算时间.2个改进算法的速度均与其对应的前N次细分参数选择有关,当给定的N较好时,改进算法的计算速度会相应地提高,当N=0时,则改进算法都退化为固定参数算法.一般而言,算法时间先随N的增大而减少,到某一N以后,算法时间随N的增大而增加.N的选择有赖于曲线的复杂度,越复杂的曲线合适的N也越大.经过多次实验验证,本次算例测试中取N=3.
|
|
表 1 曲线复杂性和算法计算时间、迭代次数算例 Table 1 Computing examples for different algorithms |
从表 1的结果可看出,在高次复杂曲线上,相对于定参法,扁平法的效果有着显著提高.而凸包法则几乎没有提高效果.凸包法本意是希望凸包面积较小的曲线容易细分逼近,实际计算情况并非如此,说明通过凸包面积控制曲线造型复杂程度不合理,不适用于改善细分算法.
在平面Bézier曲线细分过程中,假设所有曲线段每次都做细分,第i次细分需处理2i条曲线段(i=0,1,…,n),则前n次迭代共需要
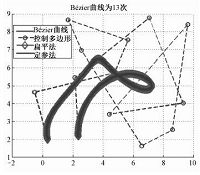
上述算例中扁平法效率提高较多的13、16、19、22次曲线,它们的细分次数比定参法少1次,算法效率就可提高70%左右,实验结果与理论分析相符(图 2,由于细分足够多,因此曲线被细分控制点完全遮挡).工程应用中,设计曲线类型复杂,因而对于未知复杂曲线有优势,细分算法是值得推荐的.其他曲线,定参法与扁平法的迭代次数相同,扁平方法略占优势.
|
Download:
|
| 图 2 效率提高较多的曲线 Fig. 2 Curves having better performance | |
可以看出,曲线形状越复杂,扁平法提高效果越好,而越接近于简单抛物线形状的曲线,扁平法和定参法效率相当.
4 结论本文研究平面Bézier曲线的细分参数选取,在传统的de Casteljau法固定细分参数的基础上,给出凸包面积最优、扁平度最优两种最优参数选取条件和算法,并且给出了加速的数值算法,实例检验表明凸包面积最优方法不适用于细分优化,算法效率没有提高效果,而扁平度最优方法效率提高优势明显,新算法对于形状复杂、次数较高的平面Bézier曲线可以有效减少细分迭代次数,大幅提高算法效率.
在CAGD应用中,曲面细分逼近应用更为广泛,我们在后继工作中将进一步进行曲面优化参数的定义和细分算法设计,并且设计基于曲面复杂性的最优优化步数N的自适应选取算法.
| [1] | Morin G, Goldman R. On the smooth convergence of subdivision and degree eleva-tion for Bézier curves[J]. Computer Aided Geometric Design , 2001, 18 (7) :657–666. DOI:10.1016/S0167-8396(01)00059-0 |
| [2] | Farin G. Curves and surfaces for CAGD[M]. 5th ed. New York: Academic Press, 2002 . |
| [3] | 郑红婵.几何造型中的若干细分方法研究及其应用 .西安:西北工业大学, 2006. http://cdmd.cnki.com.cn/article/cdmd-10699-2007214230.htm |
| [4] | 王仁宏, 李崇君, 朱春钢. 计算几何教程[M]. 北京: 科学出版社, 2008 . |
| [5] | 莫蓉, 常智勇. 计算机辅助几何造型技术[M]. 北京: 科学出版社, 2009 . |
| [6] | 汪嘉业, 王文平, 屠长河, 等. 计算几何及应用[M]. 北京: 科学出版社, 2011 . |
| [7] | Zhang M, Yan W, Yuan C M, et al. Curve fitting and optimal interpolation on CNC machines based on quadratic B-splines[J]. Science China: Information Sciences , 2011 (7) :1407–1418. |
| [8] | Wei F F, Feng J Q. Real-time rendering of algebraic B-spline surfaces via Bézier point insertion[J]. Science China: Information Sciences , 2014 (1) :71–85. |
 2016, Vol. 33
2016, Vol. 33 


