中国科学院大学学报  2016, Vol. 33 Issue (2): 283-288   PDF    
引用本文
赵钺, 黄佳, 张海峰, 李彦鹏 . 塑料浮选分离中气泡-颗粒的黏附行为[J]. 中国科学院大学学报, 2016, 33(2): 283-288.
ZHAO Yue, HUANG Jia, ZHANG Haifeng, LI Yanpeng . Bubble-particle attachment behavior in flotation process of plastics[J]. Journal of University of Chinese Academy of Sciences, 2016, 33(2): 283-288 .
塑料浮选分离中气泡-颗粒的黏附行为
赵钺1, 黄佳1, 张海峰1, 李彦鹏1,2     
1. 长安大学环境科学与工程学院, 西安 710054 ;
2. 长安大学旱区地下水文与生态效应教育部重点实验室, 西安 710054
2015年03月13日 收稿; 2015年07月07日 收修改稿
基金项目: 中央高校基本科研业务专项基金(2013G2291013)和流体动力与机电系统国家重点实验室开学基金(GZKF-201026)资助
通信作者: E-mail: liyanp01@chd.edu.cn
摘要: 采用高速摄影技术结合粘附时间模型,在实验室规格的浮选柱中研究表面活性剂浓度、类型及塑料材质对气泡在塑料球面黏附行为的影响.结果表明:气泡的最大反弹距离和黏附时间随着表面活性剂浓度的增大而逐渐减小.表面活性剂类型及塑料材质会影响气泡的黏附行为,其深层原因是表面活性剂对气泡尺寸的抑制及溶液表面张力和接触角的减小.
关键词: 表面活性剂     塑料浮选     气泡     黏附行为     高速摄影    
Bubble-particle attachment behavior in flotation process of plastics
ZHAO Yue1, HUANG Jia1, ZHANG Haifeng1, LI Yanpeng1,2     
1. School of Environmental Science and Engineering, Chang'an University, Xi'an 710054, China ;
2. Key Laboratory of Subsurface Hydrology and Ecological Effect in Arid Region of Ministry of Education, Chang'an University, Xi'an 710054, China
Abstract: To examine the bubble attachment behavior in flotation process of plastics, the high-speed photographic method, combined with a simple attachment time model, was employed in the experiments carried out in a laboratory-scale flotation column. Effects of the plastic material and the type and concentration of surfactant were analyzed in detail. Results show that the maximum rebound distance and attachment time decrease with surfactant concentration. The type of surfactant and plastic material influence bubble attachment behavior, and the reductions of the bubble size and the solution tension and contact angle are the deep incentives.
Key words: surfactant     plastic flotation     bubble     attachment behavior     high-speed photography    

塑料因其制作成本低、重量轻、多功能的优点被广泛应用于包装材料、建材、汽车及电器设备的制造.据统计，截至2010年年底世界塑料的产量已高达2.65亿t，预计今后每年仍将以8%的速率增长[1].塑料的广泛使用在给人们日常生活提供方便的同时，也带来大量的废弃塑料，不仅造成资源的巨大浪费，也给环境带来极大危害，因此塑料浮选作为一种回收再利用的有效途径得到越来越多的关注.

在塑料浮选过程中，空气作为载体以0.1~4mm范围内的小气泡形式引入[2]，与悬浮塑料颗粒碰撞并选择性黏附，形成稳定的气泡-颗粒聚合体，以达到预期的分离效果[3].因此，气泡与固体颗粒的黏附行为是浮选过程的关键所在.由于不同塑料间的润湿性相近，浮选系统中常常需要加入表面活性物质，用来修饰气-液界面的性质以及促进小气泡的产生.近年来的研究多围绕表面活性剂对气泡动力学、气含率以及分离效率的影响展开[4-5]，较少涉及气泡与固体之间的黏附行为.

本研究旨在考察塑料浮选分离中气泡-颗粒的黏附行为.为此采用高速摄影技术，在实验室规格的浮选柱中引入聚丙烯(PP)、聚乙烯(PE)和聚四氟乙烯(PTFE)小球，选择十二烷基苯磺酸钠(SDBS)、十六烷基三甲基溴化铵(CTMAB)和茶皂素(tea saponin)3种不同类型的表面活性剂，结合黏附时间模型详细研究表面活性剂浓度、类型及塑料材质对气泡在塑料球面黏附行为的影响，并深入探讨气泡黏附行为的机理.

1 材料与方法 1.1 实验材料

实验选用3种材质的塑料小球作为撞击目标，分别为聚丙烯(PP)、聚乙烯(PE)和聚四氟乙烯(PTFE)，小球直径为38mm.通过视频光学接触角测量仪(SL200KS型，Kino USA)测定的接触角确定其湿润性.经多次平行测定，纯水在PE、PP、PTFE表面的接触角分别为(90.71±0.04)°、(96.33±0.07)°和(96.24±0.06)°.实验之前对塑料小球进行预处理：用含有去污粉的自来水浸泡约20min，然后用自来水反复冲洗5~6次，室温下晾干备用.

本研究中用到的3种类型的表面活性剂纯度及基本理化性质见表 1.实验中所用溶液均采用新鲜的去离子水(18.2Ω)在20℃配制.表面活性剂的临界胶束浓度(CMC)采用表面张力法[6]测定，表面活性剂的亲水亲油平衡值(HLB)由Griffin法[7]计算得到.

表 1 3种类型的表面活性剂纯度及基本理化性质 Table 1 Three kinds of surfactants: their purities and physicochemical properties
1.2 实验装置

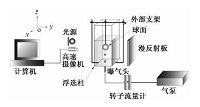
实验装置系统参考笔者先前的研究[8]，由3部分组成：气泡生成系统，气泡撞击系统和图像采集系统，如图 1所示.气泡生成系统的主体是一个15cm×15cm×800cm的有机玻璃方柱.单个气泡通过蠕动泵(BT100.01型，流量范围0.002～380mL/min)经转子流量计控制在同一流量下，向容器底部中央的喷嘴通气产生.塑料小球通过支架与刚体连接悬挂在容器内部.图像采集系统包括高速摄像仪(MS75K，Mega Speed)，金属卤化灯(DCI-2000型)，漫反射板和计算机.

Download:
图 1 实验装置示意图
Fig. 1 Schematic of the experimental apparatus
1.3 实验与分析方法

为消除气泡不稳定性的影响，将液面高度设置为400mm，塑料小球放在离底部喷嘴350mm的位置[9-10].实验测试表明气泡上升到此位置时已达到终端上升状态.所有实验均在室温(20±1)℃下的静止液体中进行，避免周围扰动.气泡的运动图像由高速摄像仪拍摄，再传送到计算机，最终由图像处理软件(AVI View)离线逐帧分析处理.拍摄的帧频为1000Hz，图像的分辨率为1280×1024像素.为提高数据分析的可靠性，每一实验条件均重复拍摄3次，取平均值计算所需参数.气泡的当量直径deq[10]由下式计算：

${{d}_{\text{eq}}}={{({{d}_{\text{v}}}d_{\text{h}}^{2})}^{1/3}},$ (1)

式中：dv和dh分别是气泡运动过程中平行及垂直方向的尺寸.

根据气泡的瞬时速度、当量直径、溶液黏度可以计算出气泡的瞬时雷诺数(Re)[11]：

$Re=\rho U{{d}_{\text{eq}}}/\mu ,$ (2)

式中，ρ为溶液密度；μ为溶液的黏度.

气泡的最大反弹距离Smax取气泡最低点和曲面的垂直距离，可以较为直观地反映碰撞过程的动能大小.气泡与塑料小球发生黏附的时间tTPC是指气泡和塑料小球之间的液膜破裂、扩张、建立稳定的润湿周界所需的时间，从气泡第一次碰撞塑料小球时算起(t=0ms).在浮选过程中黏附时间可以较为直观地反映气泡在固体表面黏附性的强弱，对浮选效率也具有一定的参考价值.

为更加深入地分析和解释实验数据，引入一个由经典润滑理论推导出的黏附时间模型[12]：

${{t}_{\text{TPC}}}=\frac{6\pi \mu R_{\text{b}}^{2}}{F}\ln \left( \frac{{{h}_{cr}}}{{{h}_{0}}} \right).$ (3)

该模型用于描述气泡在静止液体中接近二维固体表面并发生黏附的过程，假设气泡为球形，流体不可压缩，且气泡与固体表面之间的距离远小于气泡自身的尺寸.式中：h0是半径为Rb的气泡和固体表面之间的初始距离；F是作用在气泡上的驱动力；hcr是液膜即将破裂时的临界破裂厚度，Albijanic等[13]曾给出其经验公式：

${{h}_{\text{cr}}}=23.3{{\left[ \sigma (1-cos{{\theta }_{\text{a}}}) \right]}^{0.16}},$ (4)

式中，σ为表面张力；θa为接触角.

1.4 误差分析

本研究的误差主要来自实验中对气泡尺寸的测量，因其测量主要依据气泡边缘轮廓线，受人工操作测量、仪器最大分辨率限制及折射率的影响，会在确定二维图像边缘时引起误差，最大误差值为±1像素，计算气泡直径的平均误差为±4.5%～±5.1%.

2 结果与讨论 2.1 表面活性剂浓度对气泡黏附行为的影响

图 2比较同一尺寸单个气泡(deq约1.1mm)在纯水和SDBS溶液(0.00005mol/L)中撞击PP塑料小球的可视化过程.从中不难看出无论是在纯水还是在表面活性剂溶液中，气泡上升接触PP塑料小球后底部仍未停止运动并继续向上挤压造成气泡明显的形变，当形变到极限程度后气泡底部首先向下运动，整体开始远离小球反向运动.在气泡能量耗尽之前仍会往复进行这种“撞击-反弹”行为，且由于撞击时能量的消耗，气泡的第一次“撞击-反弹”行为所造成的形变程度要比之后任何一次都严重.当能量消耗殆尽后，分隔气泡与小球表面的液膜发生破裂，气泡能够完整地黏附在小球上.不同的是气泡的最大反弹距离和黏附时间存在明显的差异.

Download:
图 2 气泡撞击PP塑料小球的可视化过程图
Fig. 2 Sequential images of bubble rebound on spherical PP surface in (a) pure water and (b) SDBS solution (0.00005 mol/L)

图 3(a)给出不同浓度的SDBS溶液中气泡撞击PP塑料小球后的最大反弹距离与雷诺数之间的关系.从图中可看出纯水中气泡最大反弹距离约为气泡当量直径的1.8倍，而在加入低浓度(0.00005mol/L)的SDBS后，Smax/deq的值大幅减小，约为1.2.随着SDBS溶液浓度的增加，气泡的最大反弹距离逐渐减小，最终约等于气泡当量直径.此外对于同一浓度的SDBS溶液，随着雷诺数的增加，气泡的最大反弹距离几乎不发生变化.这表明表面活性剂的存在对气泡的最大反弹距离有显著影响，同时其浓度也有一定的影响，但Smax/deq值的变化幅度相对较小.

Download:
图 3 SDBS溶液浓度对气泡在PP表面黏附行为的影响
Fig. 3 Effects of SDBS concentration on bubble attachment behaviors on PP surface

图 3(b)进一步给出气泡撞击PP塑料小球过程中SDBS溶液浓度对黏附时间的影响.从图中可看出，无论在哪种浓度的SDBS溶液中，气泡与PP小球的黏附时间均随气泡当量直径的增大而增加.此外随着溶液浓度的增加，黏附时间呈现出减小的趋势.Krasowska等[14]在研究气泡撞击Teflon平板时也发现，低浓度的α-松油醇会大幅降低气泡与Teflon的撞击次数并明显减小tTPC.这对浮选过程中气泡尺寸和表面活性剂浓度的选择具有一定的参考价值.

运用黏附时间模型(3)进行分析，对于气泡撞击PP塑料小球，由于球面的粗糙度相对较小，气泡和球面之间的初始距h0为定值.表 2列出室温(20±1)℃下不同浓度SDBS溶液的表面张力和黏度值.从表中可明显看出，随着SDBS溶液浓度的增大，表面张力值逐渐减小，这会造成球面疏水性的降低，使PP表面接触角减小，由式(4)可知，会使hcr值减小.而溶液黏度的改变则并不明显，此外，根据笔者前期对表面活性剂影响气泡形变的研究结果[8]，当溶液中存在表面活性剂时，会减小气泡的尺寸，使Rb值减小.Kracht和Finch[15]也证实表面活性剂的加入对于浮选气泡尺寸的抑制作用.所以由黏附时间模型(3)可知，这会导致tTPC的减小.

表 2 室温(20±1)℃下不同浓度SDBS溶液的表面张力及黏度 Table 2 Surface tensions and viscosities of SDBS solutions of different concentrations at room temperature (20±1)℃
2.2 表面活性剂类型对气泡黏附行为的影响

图 4(a)比较同一浓度的SDBS、tea saponin和CTMAB 3种表面活性剂溶液(0.00005mol/L)中气泡撞击PE塑料小球后的最大反弹距离与雷诺数之间的关系.从图中可明显看出，随着雷诺数的增大，每种类型的表面活性剂溶液中Smax/deq的值基本不发生变化.当500>Re>100时，在SDBS溶液中，Smax/deq约等于1.25，而在tea saponin和CTMAB溶液中，Smax/deq约等于1.

Download:
图 4 不同类型的表面活性剂溶液对气泡在PE塑料小球表面黏附行为的影响
Fig. 4 Effects of different surfactants (0.00005mol/L) on bubble attachment behaviors on PE surface

图 4(b)进一步给出SDBS、tea saponin、CTMAB 3种不同类型的表面活性剂溶液(0.00005mol/L)中，单个气泡撞击PE球面的黏附时间随当量直径不同的变化规律.从图中可看出，随着气泡当量直径的增大，3种类型的表面活性剂溶液中气泡的黏附时间整体上呈现增加的态势.当气泡当量直径小于1.65mm时，SDBS溶液中的黏附时间最长，CTMAB溶液中的次之，tea saponin溶液中的最短；值得注意的是，当气泡当量直径大于1.65mm时，tea saponin溶液中的黏附时间大于CTMAB溶液中的.

同样运用黏附时间模型(3)进行分析，对于同一浓度不同的表面活性剂溶液中气泡撞击PE球面的过程，选取相同尺寸的气泡比较黏附时间.测得0.000 05mol/L时SDBS、CTMAB以及tea saponin溶液的表面张力值依次为75.60、62.30和75.0mN/m，PE表面接触角依次为86.59°、84.91°和74.39°.由式(4)可知，hcr值的大小为SDBS>CTMAB>tea saponin.加之小浓度的3种表面活性剂溶液黏度与纯水并无明显差别，由黏附时间模型(3)可知，黏附时间的大小应为SDBS>CTMAB>tea saponin，这也与图 4(b)所得结果相一致.

2.3 塑料的材质对气泡黏附行为的影响

图 5(a)和图 5(b)分别给出小浓度(0.00001mol/L)和大浓度(0.001mol/L)tea saponin溶液中，气泡撞击3种材质塑料小球的最大反弹距离与雷诺数之间的关系.在0.00001mol/L的tea saponin溶液中，当500>Re>100时，Smax/deq约为1.1；而在0.001mol/L的tea saponin溶液中Smax/deq约为1.0.通过对比图 5(a)和图 5(b)可看出，在tea saponin溶液中，塑料材质的不同对Smax/deq与雷诺数的关系并没有显著影响.

Download:
图 5 Tea Saponin溶液中气泡撞击3种塑料小球的最大反弹距离与雷诺数关系
Fig. 5 Normalized maximum rebound distances of bubble on different plastics surfaces in tea saponin solutions vs Re

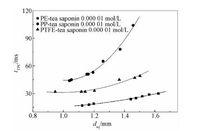
图 6比较同一浓度tea saponin溶液(0.00001mol/L)中气泡在不同塑料材质球面的黏附时间.由图可知，随着气泡当量直径由0.9mm增大到1.6mm，气泡在PP、PE、PTFE球面的黏附时间均被延长.而对于同一尺寸(1.4mm)的气泡，三者的黏附时间也存在很大差异：PP球面的黏附时间最长，约为88ms；PTFE球面次之，约为45ms；PE球面最短，约为22ms.此外，通过比较3条曲线还可看出，随着气泡当量直径的增大，PE、PP、PTFE 3种塑料球面黏附时间的差距也在逐渐增大.对于相同尺寸的气泡运用粘附时间模型(3)进行分析，由于3种塑料材质本身疏水性能不同，在加入同一相同浓度的表面活性剂后，其表面润湿的程度也不同，故3种材质的接触角也不同，因此黏附时间存在差异.

Download:
图 6 不同塑料对气泡在tea saponin溶液 (0.00001mol/L)中黏附时间的影响
Fig. 6 Effects of different plastics on the bubble attachment time in tea saponin solution (0.00001mol/L)
3 结论

1) 表面活性剂SDBS的加入使得气泡撞击PP塑料球面的Smax/deq值由纯水中的1.8下降至1.2，且随着SDBS浓度的增加，Smax逐渐减小，最终约等于deq.气泡与PP塑料球面的黏附时间随deq的增大而增加，随着SDBS浓度的增加，呈现出减小的趋势.

2) 气泡在同一浓度(0.00005mol/L)SDBS溶液中的Smax/deq约为1.25，而在tea saponin和CTMAB溶液中约为1.当气泡deq小于1.65mm时，SDBS溶液中的黏附时间最长，CTMAB溶液中的次之，tea saponin溶液中的最短.而当气泡deq大于1.65mm时，tea saponin溶液中的黏附时间大于CTMAB溶液中的.

3) 在tea saponin溶液中，塑料材质对Smax/deq并没有显著的影响.而对于同一尺寸(1.4mm)的气泡在PP球面的黏附时间最长，约为88ms；PTFE球面次之，约为45ms；PE球面最短，约为22ms.

4) 黏附时间模型的分析表明，表面活性剂对气泡尺寸的抑制及溶液表面张力和接触角的减小是造成黏附时间减小的深层次诱因.在塑料浮选过程中，可以根据气泡在不同塑料表面黏附时间的差异，快速浮选出目标塑料，这为塑料浮选中组分先后浮出的顺序提供了较好的理论依据.

参考文献
[1] 钟晓萍, 许江菱, 殷荣忠, 等. 2009-2010年世界塑料工业进展[J]. 塑料工业 , 2011, 39 (3) :1–42.
[2] Nesset J E, Hernandez-Aguilar J R, Acuna C A, et al. Some gas dispersion characteristics of mechanical flotation machines[J]. Minerals Engineering , 2006, 19 :807–815. DOI:10.1016/j.mineng.2005.09.045
[3] Firouzi M, Nguyen A V, Hashemabadi S H, et al. The effect of microhydrodynamics on bubble-particle collision interaction[J]. Minerals Engineering , 2011, 24 :973–986. DOI:10.1016/j.mineng.2011.04.005
[4] Painmanakul P, Sastaravet P, Lersjintanakarn S, et al. Effect of bubble hydrodynamic and chemical dosage on treatment of oil wastewater by induced air flotation(IAF) process[J]. Chemical Engineering Research and Design , 2010, 88 :693–702. DOI:10.1016/j.cherd.2009.10.009
[5] Lu K, Zhang X L, Zhao Y L, et al. Removal of color from textile wastewater by foam separation[J]. Journal of Hazardous Materials , 2010, 182 :928–932. DOI:10.1016/j.jhazmat.2010.06.024
[6] 朱步瑶, 赵振国. 界面化学基础[M]. 北京: 化学工业出版社, 1996 .
[7] Griffin W C. Calculation of HLB values of non-ionic surfactants[J]. Journal of Society of Cosmetic Chemists , 1954, 5 :249–256.
[8] 刘艳艳, 李彦鹏, 朱婷婷. 表面活性剂对中尺度气泡形状及速度的调控研究[J]. 西安交通大学学报:自然科学版 , 2011, 45 (10) :94–97.
[9] Li Y P, Yang L W, Zhu T T, et al. Biosurfactants as alternatives to chemosynthetic surfactants in controlling bubble behavior in the flotation process[J]. Journal of Surfactants and Detergents , 2013, 16 :409–419. DOI:10.1007/s11743-012-1401-9
[10] Li Y P, Zhu T T, Liu Y Y, et al. Effects of surfactant on bubble hydrodynamic behavior under flotation-related conditions in wastewater[J]. Water Science & Technology , 2012, 65 (6) :1060–1066.
[11] Basař ová P, Machoň V, Hubic ŭ ka M, et al. Collision processes involving a single rising bubble and a larger stationary spherical particle[J]. International Journal of Mineral Processing , 2010, 94 :58–66. DOI:10.1016/j.minpro.2009.11.004
[12] Seyyed N A, Xu Z, Masliyah J. Measurement of sliding velocity of a single micro bubble under an inclined collector surface[J]. Canadian Journal of Chemical Engineering , 2008, 86 (6) :1001–1010. DOI:10.1002/cjce.v86:6
[13] Albijanic B, Ozdemir O, Nguyen A V, et al. A review of induction and attachment times of wetting thin films between air bubbles and particles and its relevance in the separation of particles by flotation[J]. Advances in Colloid and Interface Science , 2010, 159 :1–21. DOI:10.1016/j.cis.2010.04.003
[14] Krasowska M, Zawala J, Malysa K. Air at hydrophobic surfaces and kinetics of three phase contact formation[J]. Advances in Colloid and Interface Science , 2009, 147/148 :155–169. DOI:10.1016/j.cis.2008.10.003
[15] Kracht W, Finch J A. Effect of frother on initial bubble shape and velocity[J]. International Journal of Mineral Processing , 2010, 94 :115–120. DOI:10.1016/j.minpro.2010.01.003