管道内气固颗粒粉末的输运广泛存在于化工、食品处理、电力、冶金、医药等的工业生产过程中,通过对其速度、浓度、粒度等关键参数进行在线测量,进而可以实现过程优化控制,提高生产效率、降低能耗.例如,在制药行业的固体制剂生产过程中,各生产环节之间粉体物料的精确输运已经成为改进生产工艺与提高生产质量所面临的一个重要问题;电力行业中,电厂锅炉中的煤粉颗粒与氧气的燃烧情况受输运管道送进炉膛的煤粉量影响,合理的煤粉浓度有利于提高电厂发电效率.近年来,国内外学者在粉体浓度和速度在线测量方面做了很多研究,提出一系列方法如热力学法、光学法、电容法、x射线法、静电法、微波法、图像法等[1-6].但目前此类技术应用于工业生产过程中仍然存在若干问题,例如成像测量技术,包括摄影、全息术、摄像等,因其对背景照明要求严格严重限制其现场应用范围.而光学探针常常会由于工业现场恶劣的环境条件致光学窗口污染,导致测量精度偏差较大甚至失效.由于声在传播过程中具有相较于光更强的穿透能力,加之其波长远大于微米级颗粒,受散射效应影响较小,同时,声的传播速度有限且与两相流中颗粒物紧密相关,可反映颗粒浓度和粒度信息.声衰减法对两相流的测量研究可追溯至Sewell[7]在烟雾声吸收研究中提出的多相介质声吸收理论,此后,许多研究者[8-11]陆续推导出气固/液固介质中的声传播理论模型.Millen等[12]采用60kHz的超声波测量电厂煤粉输运各管道的质量分数.Andrei和Philip[13]利用耦合项模型和单元模型研究声和电声学对悬浊液两相中颗粒的测量.国内近年来,石喜光等[14]利用被动式声发射技术测量电厂煤粉管道中弯管处煤粉浓度的研究也有很大突破.田昌等[15]对超声测量悬浊液中颗粒粒度和浓度进行了大量的理论和实验研究.本文工作关注在气固颗粒两相中超声波传播的衰减和速度随体积分数递变关系,通过自行研制的一体式超声探针,对管道内气动输运的水泥生料粉体体积分数进行在线测量技术研究.
1 理论基础超声波在气固两相介质中传播,会发生吸收、散射(衍射)和耗散等现象,声波幅值减小,即产生超声波衰减.超声波与颗粒相互作用引起的衰减主要有:1)散射,主要为超声波入射至颗粒,而向不同方向散射所致;2)黏性损失,由于颗粒相与连续相间密度差异,颗粒对气体的相对滑动产生摩擦所致;3)热损失,由于颗粒表面附近的温度梯度所致.一些学者[7-9]从微体积元中的质量、能量和动量守恒出发,建立了能够准确描述球形颗粒在两相离散系中声波动的ECAH模型,将声衰减计算最终归集为一个6阶线性方程组的求解,模型较为复杂.本文根据Lloyd 和Berry的多重散射理论[16]和Wang等[17]的改进方法预测悬浮体的声衰减α和声速v,由下式:
| $\alpha =Im\left[ {{k}_{\text{f}}}\cdot \sqrt{\left( 1+A_{0}^{'} \right)\frac{{{\phi }_{\text{m}}}{{\rho }_{\text{f}}}}{{{\rho }_{\text{s}}}}\left( 1-3A_{1}^{'}\frac{{{\phi }_{\text{m}}}{{\rho }_{\text{f}}}}{{{\rho }_{\text{s}}}} \right)+6A_{1}^{'}{{\left( \frac{{{\phi }_{\text{m}}}{{\rho }_{\text{f}}}}{{{\rho }_{\text{s}}}} \right)}^{2}}} \right],$ | (1) |
| $v=\frac{\omega }{\operatorname{Re}\left[ {{k}_{\text{f}}}\sqrt{\left( 1+A_{0}^{'} \right)\frac{{{\phi }_{\text{m}}}{{\rho }_{\text{f}}}}{{{\rho }_{\text{s}}}}\left( 1-3A_{1}^{'}\frac{{{\phi }_{\text{m}}}{{\rho }_{\text{f}}}}{{{\rho }_{\text{s}}}} \right)+6A_{1}^{'}{{\left( \frac{{{\phi }_{\text{m}}}{{\rho }_{\text{f}}}}{{{\rho }_{\text{s}}}} \right)}^{2}}} \right]}$ | (2) |
其中,
| $A_{0}^{'}=-3i\sum\limits_{n}{\left[ {{\Phi }_{n}}\frac{{{A}_{0n}}}{{{\left( {{k}_{\text{f}}}{{a}_{n}} \right)}^{3}}} \right]}$ | (3) |
| $A_{1}^{'}=3i\sum\limits_{n}{\left[ {{\Phi }_{n}}\frac{{{A}_{1n}}}{{{\left( {{k}_{\text{f}}}{{a}_{n}} \right)}^{3}}} \right]},$ | (4) |
| ${{A}_{0n}}=\frac{i\left( {{k}_{\text{f}}}{{a}_{n}} \right)}{3}\left( \frac{{{\rho }_{\text{f}}}c_{\text{f}}^{2}}{{{\rho }_{\text{s}}}c_{\text{s}}^{2}}-1 \right)-k_{\text{f}}^{2}{{a}_{n}}{{c}_{\text{f}}}{{T}_{\text{f}}}{{\rho }_{\text{f}}}{{\kappa }_{\text{f}}}H\cdot {{\left( \frac{{{\Theta }_{\text{f}}}}{{{\rho }_{\text{f}}}{{C}_{\text{pf}}}}-\frac{{{\Theta }_{\text{s}}}}{{{\rho }_{\text{s}}}{{C}_{\text{ps}}}} \right)}^{2}},$ | (5) |
| ${{A}_{1n}}=\frac{-i({{k}_{\text{f}}}{{a}_{n}})}{3}{{\left\{ \frac{3{{\rho }_{\text{f}}}}{\left( {{\rho }_{\text{s}}}-{{\rho }_{\text{f}}} \right)}+2{{\left[ 1+3\left( 1+i \right)\frac{{{\delta }_{\text{v}}}}{2{{a}_{n}}}+3i\frac{\delta _{\text{v}}^{2}}{2a_{n}^{2}} \right]}^{-1}} \right\}}^{-1}},$ | (6) |
| $H={{\left\{ \frac{1}{(1-i{{z}_{\text{f}}})}-\frac{{{\kappa }_{\text{f}}}}{{{\kappa }_{\text{s}}}}\frac{\tan ({{z}_{\text{s}}})}{\tan ({{z}_{\text{s}}})-{{z}_{\text{s}}}} \right\}}^{-1}},$ | (7) |
| $z=\frac{\left( 1+i \right){{a}_{n}}}{{{\delta }_{\text{t}}}},$ | (8) |
| ${{\delta }_{\text{v}}}=\sqrt{\frac{2{{u}_{\text{f}}}}{\omega {{\rho }_{\text{f}}}}},{{\delta }_{\text{t}}}=\sqrt{\frac{2\kappa }{\omega \rho {{C}_{\text{p}}}}}.$ | (9) |
其中,kf为入射波波数,ω为角频率,ρ是密度,μ是运动黏度,Φn是半径为an的颗粒的体积分数,A0n和A1n是半径为an单颗粒的散射系数,
图 1为一体式不锈钢超声波探针结构图,具有2个距离为6.7cm、同轴布置、设计中心频率30kHz的窄带换能器,换能器采用耐高温复合振子结构,金属外壳内壁附一层隔振耦合材料,避免收发换能器的超声波振动信号直接沿管壁传播,固定灌封胶充满着探针内超声波换能器的间隙,黏性耦合材料布置在换能器与金属贴面保护层之间,减小匹配阻抗差,保证信号的有效传播,金属贴面保护层保护超声波复合振子不受测量介质的磨损.测试了一系列不同频率超声波换能器随不同体积浓度颗粒的响应,权衡不同换能器噪声和衰减,设计中心频率为30kHz 的超声波探针用于粉体颗粒两相实验.

|
Download:
|
| 图 1 一体式超声波探针结构图 Fig. 1 Structural diagram of the integrated ultrasonic probe | |
硬件资源还包括用于产生30kHz、600V电压脉冲信号的信号发生电路;NI公司采样率100MS/s 的USB-5133数据采集卡及 PC 机一台.此外,基于LabVIEW软件编写了超声信号采集和处理软件.
2.2 实验方法在南方水泥集团杭州某水泥厂进行试验,测量对象为水泥生料粉体.图 2为测量段位置示意图,测量段管径约250cm,测量段处于弯道处,后续连有扩充弯管,水泥粉体在此处受一个离心作用,进入一个管径更大的管道进行运动,故粉体在此管段处会因离心力作用呈不均匀分布.
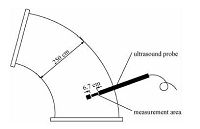
|
Download:
|
| 图 2 测量管段的纵切面示意图 Fig. 2 Longitudinal section diagram of the bend pipeline | |
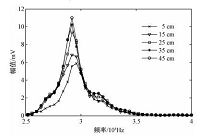
实验中,首先用热电偶测量水泥管道内的温度,其值约65℃,随后调试设备,依次把探针测量段伸入水泥粉体管道内离管壁5、15、25、35、45cm的测点,探针测量段应与水泥粉体的流向方向垂直,以保证测量的准确性.测量中,安置在一体式超声波探针中的超声波发射换能器发出超声波,经过粉体介质时信号强度和相位均发生变化,然后被布置在对面的换能器接收.为达到实时同步测量,信号发生电路会送一路同步信号至数据采集卡,记录各个测点上的信号留待后续处理,图 3即为探针在各个测量点上采集信号波形图.

|
Download:
|
| 图 3 离管壁内不同深度测点的测量数据的波形图 Fig. 3 Signal waveforms at different measurement points from the pipe wall | |
利用Lloyd 和Berry的多重散射理论[16]对空气-水泥粉体气固两相介质中的传播过程进行数值模拟,表 1给出数值模拟计算中采用的水泥粉体和65℃时空气的物理参数.
|
|
表 1 水泥粉体和65℃空气的物理参 Table 1 hysical properties of cement powder and air at 65℃ |
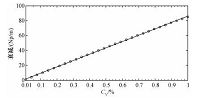
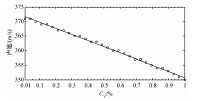
数值模拟中,选取频率为30kHz的超声波,在显微镜下观察得水泥样品粉体平均直径27.8μm,设定体积分数变化范围从0.01%到1%,图 4给出此条件下超声衰减与粉体体积分数的关系,根据数值模拟出来的结果进行最小二乘拟合.可见,随粉体体积分数增大,声衰减呈线性递增,拟合合理.图 5为超声波声速与粉体体积分数的关系,随粉体体积分数增加,超声波传播速度呈线性减少.
|
Download:
|
| 图 4 30kHz超声波衰减随粉体体积分数的变化关系 Fig. 4 Ultrasonic attenuation versus the powder volume concentration | |
|
Download:
|
| 图 5 30kHz超声波声速随粉体体积分数的变化关系 Fig. 5 Ultrasound velocity versus the powder volume concentration | |
试验中气固两相流中的超声衰减系数αs
| ${{\alpha }_{\text{s}}}=\frac{\ln \left( {{A}_{0}}/{{A}_{1}} \right)}{L},$ | (10) |
其中,L为声程,即发射与接收探头之间距离,A0和A1是空气(背景)和粉体分别经过测量区时,换能器接收的超声波幅值.
根据理论模型和数值分析的结果,可知对于给定频率,在一定浓度范围内,超声衰减系数与粉体体积分数CV之间存线性关系,如下
| ${{\alpha }_{\text{s}}}=m{{C}_{\text{V}}}+n,$ | (11) |
其中,m和n是常数,由图 4中拟合数据给出式(11)具体表达式αs=9554.23CV+1.18.这样,通过实验分别测得声压幅值A0和A1,利用式(10)计算声衰减系数αs,代入式(11)即可得到粉体的体积分数.
图 6为一体式超声波探针在管壁不同距离测点获得信号的幅度谱图,表 2给出在不同测点的具体幅值和粉体体积分数结果.很明显在沿管道径向方向,随着探针测点离管壁距离增大,测得信号幅值也相应增加,超声波衰减越小,表 2结果说明距离管壁越远,水泥粉体的体积分数越小.
|
Download:
|
| 图 6 不同测量点波形信号的频谱图 Fig. 6 Frequency spectrogram of signal waveforms at different measurement points | |
|
|
表 2 超声衰减浓度测量结果 Table 2 Measured results using the method of ultrasonic attenuation |
为做声速法分析,实验中首先获取单相空气中信号S0,再获取粉体通过测量区时信号S1,信号S0和S1之间存有波形相位差
| ${{R}_{{{S}_{0}}{{S}_{1}}}}(\Delta t)=E({{S}_{0}}{{S}_{1}})=\underset{T\to \infty }{\mathop{\lim }}\,\frac{1}{T}\int_{0}^{T}{{{S}_{0}}{{S}_{1}}\text{d}t}.$ | (12) |
对两信号先滤波再根据式(12)作互相关运算,得到波形间的时间延迟Δt,这样,以单相空气中声速c0为参照(c0=331.3+0.606t0,t0是摄氏温度),根据式(13)求得两相介质中声速c1(S0和S1测量时环境温度须一致,或做温度修正).
| ${{c}_{1}}=1/\left( \frac{1}{{{c}_{0}}}-\frac{\Delta t}{L} \right).$ | (13) |
表 3列出探针在不同测点实验数据.延迟时间Δt随着探针伸入管道深度而逐渐减小,超声波声速则随着管道深度而相应增大.按照图 5拟合关系式c1=-6832CV+366.97,进一步计算各测点的粉体体积分数.结果表明,管内粉体在截面上分布不均匀,距离管壁越远,粉体体积分数明显越小.表中数据也印证了超声波在气固两相中传播时,随着颗粒浓度的增加,声速变小.
|
|
表 3 超声声速法粉体浓度测量结果 Table 3 Measured results using the method of ultrasound velocity |
图 7为两种方法测得管内粉体体积分数沿管径分布图,可以明显观察到两种方法测量的结果变化趋势一致,随着测点离管壁距离增加,粉体体积分数减小,这是由于实验在水泥粉体输运管段一弯管处进行,水泥粉所受离心力作用造成该弯管半径大处水泥粉体体积分数高.同时,从图中还可看出,声速法测量体积分数值整体上大于衰减法结果,鉴于实验中已尽可能保证了温度和湿度等环境条件,所以二者的差异很可能是由于粉体形状或者相互粘连对声衰减的影响造成,此时声速往往对体积分数含量本身更为敏感.
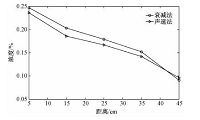
|
Download:
|
| 图 7 管内水泥生料粉体体积分数沿管径分布 Fig. 7 Distribution of cement powder volume fraction along the diameter of pipeline | |
采用一体式低频超声波探针对水泥粉输运管道一弯管段内水泥粉体的体积分数进行测量,分别利用超声衰减法和声速法获得沿管径方向分布的水泥粉体体积分数.两种方法结果都表明从管壁处沿着管径方向水泥粉体的体积分数逐渐减小,该变化趋势也反映出弯管段测量的特征.本文所采用方法可为管内粉体体积分数的实时在线测量提供一种行之有效的手段.
| [1] | 孙猛, 刘石, 雷兢, 等. 电厂送粉系统煤粉浓度和速度的在线测量技术研究[J]. 热能动力工程 , 2009, 24 (2) :211–215. |
| [2] | 许传龙, 宋志英, 王式民, 等. 静电传感技术在燃煤电站煤粉测量中的应用[J]. 锅炉技术 , 2008, 39 (1) :32–37. |
| [3] | 范卫东, 章明川, 何磊, 等. 管道内气固两相流颗粒浓度和风速测量方法的试验研究[J]. 仪器仪表学报 , 2003, 24 (1) :13–18. |
| [4] | 苗春卫, 李玉祥, 王克家, 等. 基于数字图像处理的煤粉颗粒检测[J]. 应用科技 , 2003, 30 (2) :31–34. |
| [5] | 秦授轩, 蔡小舒. 在线测量煤粉粒度分布和浓度的实验研究[J]. 中国电机工程学报 , 2010, 30 (32) :30–34. |
| [6] | Yan Y, Byrne B. Measurement of solids deposition in pneumatic conveying[J]. Powder Technology , 1997, 91 (1) :131–139. |
| [7] | Sewell C J T. On the extinction of sound in viscous atmospheres by small obstacles of cylindrical form[J]. Philosophical Transactions of the Royal Society A , 1910, 210 :239–270. |
| [8] | Epstein P S, Carhart R R. The absorption of sound in suspensions and emulsions,I.Water fog in air[J]. Journal of the Acoustical Society of America , 1953, 25 (3) :553–565. DOI:10.1121/1.1907107 |
| [9] | Allegra J R, Hawley S A. Attenuation of Sound in Suspensions and Emulsions[J]. Journal of the Acoustical Society of America , 1972, 51 (1) :1545–1564. |
| [10] | Allegra J R, Hawley S A. Propagation of sound through a liquid containing bubbles[J]. Journal of the Acoustical Society of America , 1947, 19 (3) :481–501. DOI:10.1121/1.1916508 |
| [11] | McClements D J. Ultrasonic characterization of emulsions and suspensions[J]. Advances in Colloid and Interface Science , 1991, 37 (1) :33–72. |
| [12] | Andrei S D, Philip J G. Acoustic and electroacoustic spectroscopy for characterizing concentrated dispersions and emulsions[J]. Advances in Colloid and Interface Science , 2001, 92 :73–132. DOI:10.1016/S0001-8686(00)00035-X |
| [13] | Millen M J, Sowerby B D, Coghill P J, et al. Plant tests of an on-line multiple-pipe pulverized coal mass flow measuring system[J]. Flow Measurement and Instrumentation , 2000, 11 (3) :153–158. DOI:10.1016/S0955-5986(00)00013-3 |
| [14] | 石喜光, 周昊, 岑可法. 基于超声波方法的管内气固两相流浓度测量技术[J]. 热力发电 , 2005 (5) :44–64. |
| [15] | 田昌, 苏明旭, 蔡小舒. 基于超声法测量气固两相流浓度实验研究[J]. 工程热物理学报 , 2013, 34 (8) :1487–1490. |
| [16] | Uoyd P, Berry M V. Wave propagation through an assembly of spheres. Part Ⅳ. Relations between different scattering theories[J]. Proceedings of the physical Society , 1967, 91 :678–688. DOI:10.1088/0370-1328/91/3/321 |
| [17] | Wang Q. Particle irregularity and aggregation effects in airborne suspensions at audio and low ultrasonic frequencies[J]. Journal of Sound and Vibration , 2000, 236 (5) :781–800. DOI:10.1006/jsvi.1999.3032 |
 2016, Vol. 33
2016, Vol. 33 


