作为一种新兴的能源利用技术,双循环流化床技术近年来被广泛应用于节能减排与新能源开发中.得益于双循环流化床的特殊结构,可以实现针对包括燃烧、气化和热解在内的由多个子反应构成的热化学转化过程的解耦控制,从而达到加强或抑制热化学转化中某些特定产物和反应的生成与进行的目的,进而实现能量与物质的联合产出、区分利用[1-5].然而,双循环流化床内复杂的气固流动特性给双循环流化床的设计、研究与运行带来一定困难,因而针对其内部气固流动特性的研究吸引了国内外的广泛重视.特别是双循环流化床内的颗粒分布特性作为装置中热化学反应过程的一个重要影响因素,对构建反应器间物料循环利用及提高热化学反应效率有着关键的作用.然而颗粒分布特性在实验中较难获得,在此背景下本文通过构建双循环流化床数值模拟平台开展三维尺度下的双循环流化床内颗粒分布特性研究.
1 数理模型 1.1 数学模型 1.1.1 控制方程本文采用欧拉-欧拉模型用于描述双循环流化床内的气固流动,离散的固体颗粒相被假设为颗粒尺寸与密度均一致的一种假想连续介质,从而实现应用相同形式的流体动力学方程描述气相与固相的混合流动.气相与固相的连续性方程描述如下
| $\frac{\partial }{\partial t}({{\varepsilon }_{\text{g}}}{{\rho }_{\text{g}}})+\nabla ({{u}_{\text{g}}}{{\varepsilon }_{\text{g}}}{{\rho }_{\text{g}}})=0$ | (1) |
| $\frac{\partial }{\partial t}({{\varepsilon }_{\text{s}}}{{\rho }_{\text{s}}})+\nabla ({{u}_{\text{s}}}{{\varepsilon }_{\text{s}}}{{\rho }_{\text{s}}})=0,$ | (2) |
| ${{\varepsilon }_{\text{g}}}+{{\varepsilon }_{\text{s}}}=1,$ | (3) |
式中,ug和us分别为气相与固相的速度,ρg和ρs分别为气相与固相的密度,εg和εs则分别为气相与固相的体积分数.
动量守恒方程如下
| $\begin{align} & \frac{\partial }{\partial t}({{u}_{\text{g}}}{{\varepsilon }_{\text{g}}}{{\rho }_{\text{g}}})+\nabla ({{u}_{\text{g}}}{{u}_{\text{g}}}{{\varepsilon }_{\text{g}}}{{\rho }_{\text{g}}})={{\varepsilon }_{\text{g}}}\nabla {{\tau }_{\text{g}}}- \\ & {{\rho }_{\text{g}}}\nabla P+\beta \left( {{u}_{\text{s}}}-{{u}_{\text{g}}} \right)+{{\varepsilon }_{\text{g}}}{{\rho }_{\text{g}}}g, \\ \end{align}$ | (4) |
| $\begin{align} & \frac{\partial }{\partial t}({{u}_{\text{s}}}{{\varepsilon }_{\text{s}}}{{\rho }_{\text{s}}})+\nabla ({{u}_{\text{s}}}{{u}_{\text{s}}}{{\varepsilon }_{\text{s}}}{{\rho }_{\text{s}}})={{\varepsilon }_{\text{s}}}\nabla {{\tau }_{\text{s}}}- \\ & {{\rho }_{\text{s}}}\nabla P-\nabla {{P}_{\text{s}}}+\beta \left( {{u}_{\text{g}}}-{{u}_{\text{s}}} \right)+{{\varepsilon }_{\text{s}}}{{\rho }_{\text{s}}}g, \\ \end{align}$ | (5) |
式中,g为重力加速度,β为气固相间的曳力系数,τg和τs分别为气固两相的应力张量.
1.1.2 封闭方程本构方程被引入用于满足控制方程的封闭条件.标准k-ε湍动模型被用于对气相中湍动流动的描述,在不考虑分散的颗粒对气相作用的情况下,湍动能(k)方程和动能耗散率(ε)方程表述如下
| $\begin{align} & \frac{\partial }{\partial t}({{\varepsilon }_{\text{g}}}{{\rho }_{\text{g}}})+\nabla ({{u}_{\text{g}}}{{\varepsilon }_{\text{g}}}{{\rho }_{\text{g}}}k)={{\varepsilon }_{\text{g}}}{{G}_{k}}-({{\varepsilon }_{\text{g}}}{{\rho }_{\text{g}}})\varepsilon + \\ & \nabla \left( {{\varepsilon }_{\text{g}}}\frac{{{\mu }_{\text{t}}}}{{{\sigma }_{k}}}\nabla {{k}_{\text{g}}} \right)+{{\varepsilon }_{\text{g}}}{{\rho }_{\text{g}}}{{\prod }_{k}}, \\ \end{align}$ | (6) |
| $\begin{align} & \varepsilon \left\{ \frac{\partial }{\partial t}({{\varepsilon }_{\text{g}}}{{\rho }_{\text{g}}})+\nabla ({{u}_{\text{g}}}{{\varepsilon }_{\text{g}}}{{\rho }_{\text{g}}}) \right\}=\frac{{{\varepsilon }_{\text{g}}}\varepsilon }{{{k}_{\text{g}}}}\left[ {{C}_{1}}{{G}_{k}}-{{C}_{2}}\varepsilon {{\rho }_{\text{g}}} \right]+ \\ & \nabla \left( {{\varepsilon }_{\text{g}}}\frac{{{\mu }_{\text{t}}}}{{{\sigma }_{\varepsilon }}}\nabla \varepsilon \right)+{{\varepsilon }_{\text{g}}}{{\rho }_{\text{g}}}{{\prod }_{\varepsilon }}, \\ \end{align}$ | (7) |
式中,常数分别为c1=1.44,c2=1.92,cμ=0.09,σk=1.0,σε=1.3,而Gk则为
| ${{G}_{k}}={{\mu }_{\text{t}}}\left[ \nabla {{u}_{\text{g}}}+{{\left( \nabla {{u}_{\text{g}}} \right)}^{\text{T}}} \right]:\nabla {{u}_{\text{g}}}.$ | (8) |
颗粒动力学理论通过使用颗粒拟温度(Θs)作为衡量固相颗粒脉动动能的方法,而颗粒拟温度可以通过如下的固相湍动能输运方程的求解获得
| $\begin{align} & \frac{3}{2}\left[ \frac{\partial }{\partial t}({{\varepsilon }_{\text{s}}}{{\rho }_{\text{s}}}{{\Theta }_{\text{s}}})+\nabla ({{u}_{\text{s}}}{{\varepsilon }_{\text{s}}}{{\rho }_{\text{s}}}{{\Theta }_{\text{s}}}) \right]=\nabla \left( {{k}_{{{\Theta }_{\text{s}}}}}\nabla {{\Theta }_{\text{s}}} \right)+ \\ & \left( {{\tau }_{\text{s}}}-\nabla {{P}_{s}}I \right):\nabla {{u}_{\text{s}}}+{{\phi }_{\text{gs}}}-{{\gamma }_{{{\Theta }_{\text{s}}}}}. \\ \end{align}$ | (9) |
由于式中的对流项和扩散项对结果的求解几乎没有影响,可以得到简化的用于颗粒拟温度计算的代数表达式
| ${{\gamma }_{{{\Theta }_{\text{s}}}}}=\left( {{\tau }_{\text{s}}}-{{P}_{s}}I \right):\nabla {{u}_{\text{s}}}.$ | (10) |
考虑到颗粒相浓度较高时颗粒间的相互作用主要由摩擦力决定,颗粒相剪切黏度首先被引入
| ${{\mu }_{\text{s}}}={{\mu }_{\text{s,kin}}}+{{\mu }_{\text{s,col}}}+{{\mu }_{\text{s,fri}}}.$ | (11) |
本文采用Syamlal模型[6]用于剪切黏度的描述,动力黏度项μs,kin表述如下
| ${{\mu }_{\text{s,kin}}}=\frac{{{\varepsilon }_{\text{s}}}{{\rho }_{\text{s}}}{{d}_{\text{s}}}\sqrt{\frac{{{\Theta }_{\text{s}}}}{\text{ }\!\!\pi\!\!\text{ }}}}{6\left( 3-e \right)}\left[ 1+\frac{2{{\varepsilon }_{\text{s}}}{{g}_{0}}}{5}\left( e+1 \right)\left( 3e-1 \right) \right].$ | (12) |
颗粒相的碰撞黏度项μs,col为
| ${{\mu }_{\text{s,col}}}=\frac{4}{5}{{\varepsilon }_{\text{s}}}{{\rho }_{\text{s}}}{{d}_{\text{s}}}{{g}_{0}}\left( e+1 \right)\sqrt{\frac{{{\Theta }_{\text{s}}}}{\text{ }\!\!\pi\!\!\text{ }}}.$ | (13) |
由Shaeffer等[7]提出的摩擦黏度项表述为
| ${{\mu }_{\text{s,fri}}}=\frac{{{P}_{\text{s,fri}}}\sin \left( \psi \right)}{2\sqrt{{{I}_{2\text{D}}}}},$ | (14) |
式中,ψ表示颗粒间摩擦的角度,本文中被设置为28.5°[8-9].
由Lun等[10]提出的颗粒相压力表达式为
| ${{P}_{\text{s}}}={{\varepsilon }_{\text{s}}}{{\rho }_{\text{s}}}{{\Theta }_{\text{s}}}\left[ 2{{\varepsilon }_{\text{s}}}{{g}_{0}}\left( e+1 \right)+1 \right].$ | (15) |
径向分布函数则为
| ${{g}_{0}}=\left[ 1-{{\left( \frac{{{\varepsilon }_{\text{s}}}}{{{\varepsilon }_{\text{s,max}}}} \right)}^{-2.5{{\varepsilon }_{\text{s,max}}}}} \right].$ | (16) |
颗粒相体积黏度被用作对颗粒相对压缩或膨胀的阻力的描述
| ${{\lambda }_{\text{s}}}=\frac{4}{3}{{\varepsilon }_{\text{s}}}{{\rho }_{\text{s}}}{{d}_{\text{s}}}{{g}_{0}}\left( e+1 \right)\sqrt{\frac{{{\Theta }_{\text{s}}}}{\text{ }\!\!\pi\!\!\text{ }}}.$ | (17) |
由颗粒碰撞和气固相间脉动能传递导致的脉动能耗散率分别为
| ${{\gamma }_{\text{s}}}=3\varepsilon _{\text{s}}^{2}{{\rho }_{\text{s}}}{{g}_{0}}\theta \left( 1-{{e}^{2}} \right)\left( \frac{4}{{{d}_{\text{s}}}}\sqrt{\frac{\theta }{\text{ }\!\!\pi\!\!\text{ }}}-\nabla {{u}_{\text{s}}} \right),$ | (18) |
| ${{\phi }_{\text{gs}}}=-3\beta {{\theta }_{\text{s}}}.$ | (19) |
曳力是流化床反应器内气固相间的主要作用力,考虑到曳力对动量守恒方程求解的重要影响,多个修正曳力模型基于不同的假设被提出,主要有Syamlal-O’brien曳力模型[11]、Wen-Yu曳力模型[12]和Gidaspow曳力模型[13].本文所采用Syamlal-O’brien曳力模型表述如下
| $\beta =\frac{3{{\varepsilon }_{\text{s}}}{{\varepsilon }_{\text{g}}}{{\rho }_{\text{g}}}{{C}_{\text{D}}}\left| {{u}_{\text{g}}}-{{u}_{\text{s}}} \right|}{4u_{\text{r,s}}^{2}{{d}_{\text{s}}}}\left( \frac{{{\operatorname{Re}}_{\text{s}}}}{u_{\text{r,s}}^{2}} \right),$ | (20) |
式中曳力系数(CD)表述如下
| ${{C}_{\text{D}}}=\left( 0.63+4.8\sqrt{\frac{u_{\text{r,s}}^{2}}{{{\operatorname{Re}}_{\text{s}}}}} \right),$ | (21) |
| ${{\operatorname{Re}}_{\text{s}}}=\frac{{{\varepsilon }_{\text{g}}}{{\rho }_{\text{g}}}{{d}_{\text{s}}}\left| {{u}_{\text{g}}}-{{u}_{\text{s}}} \right|}{{{\mu }_{\text{g}}}}.$ | (22) |
终端速度则按照Garside&Al-Dibouni终端速度表达式表述为
| $\begin{align} & {{u}_{\text{r,s}}}=0.5\left[ A-0.06{{\operatorname{Re}}_{\text{s}}} \right.+ \\ & \left. \sqrt{{{A}^{2}}-0.12{{\operatorname{Re}}_{\text{s}}}\left( 2B-A \right)+{{\left( 0.06{{\operatorname{Re}}_{\text{s}}} \right)}^{2}}} \right], \\ \end{align}$ | (23) |
| $\begin{align} & A=\varepsilon _{\text{g}}^{4.14} \\ & B=\left\{ \begin{matrix} 0.8\varepsilon _{\text{g}}^{1.28}, & {{\varepsilon }_{\text{g}}}\le 0.85, \\ \varepsilon _{\text{g}}^{2.65}, & {{\varepsilon }_{\text{g}}}>0.85. \\ \end{matrix} \right. \\ \end{align}$ | (24) |
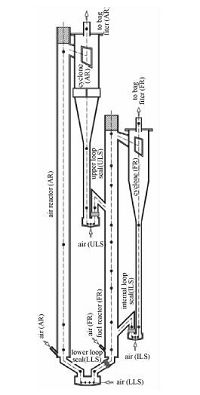
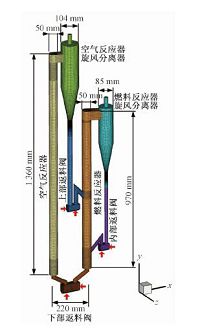
维也纳科技大学的Pröll等[14]设计了一台如图 1所示的冷态实验装置用于双循环流化床内流体动力学特性的研究.其主要结构参数如表 1所示,来源于Kolbitsch等[15]建立的实验室热态双循环流化床反应器装置的按比例缩小.本文依据此冷态实验装置建立了如图 2所示的模型用于双循环流化床的气固流动特性数值模拟研究.
|
Download:
|
| 图 1 冷态实验装置结构简图[14] Fig. 1 Sketch of the cold flow model | |
|
|
表 1 主要物理与计算参数 Table 1 Main geometrical and computational parameters for simulation |
|
Download:
|
| 图 2 三维双循环流化床模型 Fig. 2 3-dimensional dual circulating fluidized bed model | |
双循环流化床内气相与固相初始速度均设置为0,总质量为5kg的固体颗粒被分别堆积于空气反应器、燃料反应器、返料阀及下降管中,其初始体积分数为0.6.空气反应器与燃料反应器的流化风分别通过绕反应器圆周间隔90°布置的4个喷嘴进入装置内,返料风则分别经由设置在底面与侧面的2个入口进入返料阀内(在图 2中由红色箭头标注),上述气体入口均为速度入口.空气反应器与燃料反应器的旋风分离器出口均被设置为压力出口.双循环流化床内壁面假设均为无滑移无渗透的壁面.
物理模型的网格划分通过Gambit完成,网格划分方法上采用结构化网格与非结构化网格混合的方式,使用四面体与六面体混合构建网格.经网格敏感性分析后选取单元总数为26.4万的网格用于数值计算.时间步长选取为10-4s,每个时间步长的最大迭代次数为20次.
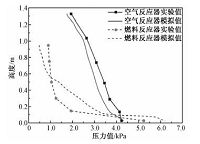
2 结果与讨论 2.1 模型验证采用标准工况(空气反应器流化气量30.3m3/h,燃料反应器流化气量10m3/h,底部返料阀返料风量1.5m3/h,上部返料阀返料风量1.5m3/h,内部返料阀返料风量0.15m3/h,存料量5kg)对双循环流化床内的气固流动进行数值模拟,并取运行稳定后双循环流化床空气反应器与燃料反应器内轴向压力分布的时间平均值与实验所得数据[6]进行对比,其结果如图 3所示.
|
Download:
|
| 图 3 轴向压力分布模拟值与实验值对比 Fig. 3 Comparison of axial pressure profiles between simulation and experiment results | |
可以发现空气反应器内压力曲线的模拟值与实验值吻合较好,最大误差小于10%;而在燃料反应器侧,上部返料阀、内部返料阀和底部返料阀结构设计参数与所选冷态实验装置原型的差异导致返料特性的改变,使得燃料反应器内压力曲线的模拟值相比实验值存在一定的差异.由于上部返料阀流出物料的速度相对实验有所增大,造成物料流出上部返料阀后分布于燃料反应器整个截面而不是大量沿内壁下落,使得燃料反应器中部压力相比实验值有所增大;同理,由内部返料阀送入的物料进入燃料反应器底部的速度相比实验工况也较大,使得底部压力同样表现出较实验值增大的特征.然而燃料反应器内轴向压力曲线的实验数据与模拟数据均表现出一致的变化趋势,压力曲线在燃料反应器中下部区域增长较快同时在反应器上部区域增长较缓.因而,所用模型适于对双循环流化床内的气固流动特性进行深入研究.
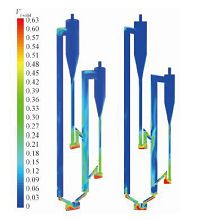
2.2 双循环流化床内稳定流态当装置内部气固流动达到稳定运行状态之后,空气反应器与燃料反应器中形成快速流化态.图 4显示在某个稳定运行的时刻,双循环流化床内颗粒相的全场分布形态.系统内气固流动分别构成流经空气反应器上升管、空气反应器旋风分离器、上部返料阀、燃料反应器上升管、下部返料阀的全局循环和流经燃料反应器上升管、燃料反应器旋风分离器、内部返料阀的内部循环.可以看到,燃料反应器内部气固流动由于同时受到上部反料阀与内部返料阀的影响而相对复杂,燃料反应器上升管的中部区域与底部区域颗粒浓度相对较高.处于燃料反应器底部的颗粒群被上升气流携带向上运动时与返料阀出口流出的具有向下速度矢量的颗粒群混合形成低速颗粒团,从而在返料阀出口区域形成颗粒浓相区,同时内部返料阀出口下方与上部返料阀出口上方均有稀相区域形成.
|
Download:
|
| 图 4 双循环流化床内稳定运行状态颗粒分布 Fig. 4 Solid distribution in dual circulating fluidized bed during steady operation | |
截面的径向颗粒浓度分布是表征反应器内气固流动特性的重要参数,上述双循环流化床由于包含全局循环与内部循环两种颗粒循环回路且装置内连通结构较为复杂,使得空气反应器与燃料反应器内的截面径向颗粒浓度均表现出特殊的分布特性.
标准工况下空气反应器内0.35、0.70、1.05m高度截面的x轴与z轴径向颗粒分布如图 5(a)所示.由下部返料阀进入空气反应器的颗粒受结构设计的影响带有的x轴负向速度矢量造成颗粒在远离下部返料阀一侧壁面附近堆积,造成所选取3个高度截面上的x轴径向颗粒浓度均表现出负向近壁面区域浓度较高的特征.z轴径向颗粒浓度分布受出口弯管偏向z轴负向13°的影响,z轴正向近壁面区域颗粒浓度相对负向近壁面区域稍高,但z轴径向分布整体为中间低两边高并表现出明显的轴对称性.
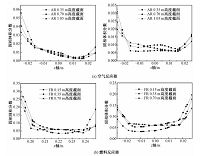
|
Download:
|
| 图 5 不同高度截面颗粒浓度径向分布 Fig. 5 Radial solid concentration distributions at different heights | |
运行于标准工况时的燃料反应器内0.15、0.35、0.70m高度截面的x轴与z轴径向颗粒分布如图 5(b)所示,各个截面上的x轴与z轴径向颗粒分布均具有中间低两边高的特征.而由于燃料反应器侧上部返料阀与内部返料阀出口分别设置在x轴负向和正向,使得燃料反应器内的颗粒浓度在x轴径向上表现出明显的不对称性,尤其是0.15m高度与0.70m高度截面均表现为x轴负向近壁面颗粒浓度明显高于x轴正向近壁面颗粒浓度,0.35m高度则因为受到上部返料阀进入燃料反应器物料的影响使得x轴正向近壁面颗粒浓度明显增大.
2.4 燃料反应器(FR)内截面径向颗粒浓度分布受FR流化气量的影响燃料反应器作为全局循环与内部循环共同的关键构成部分对双循环流化床反应器的反应效率具有重要影响[16],而燃料反应器流化气量对于借由改变内部气固接触条件以调节气固反应效率具有明显作用[17].研究不同燃料反应器流化气量条件下燃料反应器内各个高度截面径向颗粒分布变化特征对于全面了解双循环流化床的气固流动特性及针对其内部气固流动的优化具有重要意义.
燃料反应器流化气量分别设置为7.5、10.0、12.5、15.0和17.5m3/h,达到稳定运行后燃料反应器内截面高度分别为0.15、0.35和0.70m的径向颗粒分布如图 6所示.
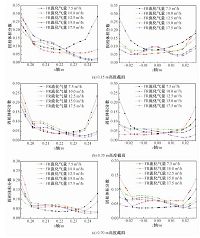
|
Download:
|
| 图 6 不同流化气量燃料反应器不同高度截面颗粒浓度径向分布 Fig. 6 Radial solid concentration distributions at different heghts in FR at different FR fluidization flow rates | |
通过对比对应不同燃料反应器流化气量的截面径向颗粒浓度分布可以发现,燃料反应器所选3个高度截面的x轴正向近壁面区域的颗粒浓度随着流化气量的增加迅速减小并在流化气量达到12.5m3/h后趋于稳定;而在x轴负向近壁面区域则表现出颗粒浓度随流化气量先增大后减小随后再次增大的趋势.另一方面,z轴正向与负向近壁面区域在所选高度上均表现出颗粒浓度随流化气量增大而减小的特征.此外,结合x轴方向与z轴方向的颗粒浓度径向分布曲线,可以发现0.15m高度截面的上中间区域颗粒浓度随流化气量增大而增大,而0.35m与0.70m高度截面的中间区域颗粒浓度则随流化气量先增大后减小.
3 结论本文基于欧拉-欧拉模型并耦合标准k-ε湍流方程模型与颗粒动理学理论,对双循环流化床内气固流动进行三维数值模拟.结果表明:
1) 空气反应器中与燃料反应中形成快速流化态.受燃料反应器所连接返料阀的返料影响,在上部返料阀出口上方与内部返料阀出口下方形成空腔型稀相区.
2) 使用标准工况的参数设定时,空气反应器与燃料反应器所研究高度截面的x轴与z轴径向颗粒浓度分布均表现出U型分布特征.空气反应器0.35、0.70、1.35m高度截面x轴径向颗粒浓度均表现出负向近壁面区域明显较高的特征;z轴径向颗粒浓度分布受出口弯管偏向z轴负向的影响,z轴正向近壁面区域颗粒浓度相对负向近壁面区域稍高.燃料反应器0.15、0.35和0.70m高度截面的径向颗粒浓度分布均表现出近壁面浓度较高的特征,而由于上部返料阀与内部返料阀出口分别设置在x轴的负向与正向,使得x轴方向的径向颗粒浓度分布尤其是在0.15m高度与0.70m高度截面上表现出明显的不对称性.
3) 改变燃料反应器流化气量,分别设置为7.5、10.0、12.5、15.0和17.5m3/h.在燃料反应器内0.15、0.35、0.70m高度截面上,x轴正向近壁面区域颗粒浓度随着流化气量的增加迅速减小并在流化气量达到12.5m3/h后趋于稳定,x轴负向近壁面区域颗粒浓度随流化气量先增大后减小随后再次增大;z轴正向与负向近壁面区域在不同高度上均表现出颗粒浓度随流化气量增大而减小的特征;此外,0.15m高度截面中间区域的颗粒浓度随流化气量增大而增大,而0.35m与0.70m高度截面的中间区域颗粒浓度则随流化气量先增大后减小.
| [1] | Kolbitsch P, Pröll T, Bolhar-Nordenkampf J, et al. Design of a chemical looping combustor using a dual circulating fluidized bed (DCFB) reactor system[J]. Chemical Engineering & Technology , 2009, 32 (3) :398–403. |
| [2] | Seo M W, Goo J H, Kim S D, et al. Gasification characteristics of coal/biomass blend in a dual circulating fluidized bed reactor[J]. Energy & Fuels , 2010, 24 (5) :3108–3118. |
| [3] | Pröll T, Kolbitsch P, Bolhàr-Nordenkampf J, et al. A novel dual circulating fluidized bed system for chemical looping processes[J]. AIChE journal , 2009, 55 (12) :3255–3266. DOI:10.1002/aic.11934 |
| [4] | 初雷哲, 范晓旭, 肖琦, 等. 双循环流化床生物质解耦气化实验[J]. 农业机械学报 , 2010, 41 :117–120. |
| [5] | 于旷世. 循环流化床双床煤气化工艺试验研究[D]. 北京:中国科学院工程热物理研究所, 2012. http://cdmd.cnki.com.cn/article/cdmd-80135-1012418683.htm |
| [6] | Syamlal M, Rogers W, O'Brien T J. MFIX documentation: theory guide J. Technical Note[R]. DOE/METC-94/1004, NTIS/DE94000087, National Technical Information Service, Springfield, VA, 1993. |
| [7] | Schaeffer D G. Instability in the evolution equations describing incompressible granular flow[J]. Journal of Differential Equations , 1987, 66 (1) :19–50. DOI:10.1016/0022-0396(87)90038-6 |
| [8] | Srivastava A, Sundaresan S. Analysis of a frictional-kinetic model for gas-particle flow[J]. Powder Technology , 2003, 129 (1) :72–85. |
| [9] | Wang S, Yang Y, Lu H, et al. Computational fluid dynamic simulation based cluster structures-dependent drag coefficient model in dual circulating fluidized beds of chemical looping combustion[J]. Industrial & Engineering Chemistry Research , 2012, 51 (3) :1396–1412. |
| [10] | Lun C K K, Savage S B, Jeffrey D J, et al. Kinetic theories for granular flow: inelastic particles in Couette flow and slightly inelastic particles in a general flowfield[J]. Journal of Fluid Mechanics , 1984, 140 :223–256. DOI:10.1017/S0022112084000586 |
| [11] | Syamlal M, O'Brien T J. The derivation of a drag coefficient formula from velocity-voidage correlations[R]. Department of Energy, Office of Fossil Energy, Technical report, 1994. |
| [12] | Wen C, Yu Y H. Mechanics of fluidization[J]. Chem Eng Prog Symp Ser , 2014, 62 (62) :100. |
| [13] | Gidaspow D. Multiphase flow and fluidization: continuum and kinetic theory descriptions[M]. Academic Press, 1994 . |
| [14] | Pröll T, Rupanovits K, Kolbitsch P, et al. Cold flow model study on a dual circulating fluidized bed (DCFB) system for chemical looping processes[J]. Chemical Engineering & Technology , 2009, 32 (3) :418–424. |
| [15] | Kolbitsch P, Pröll T, Bolhar-Nordenkampf J, et al. Design of a chemical looping combustor using a dual circulating fluidized bed (DCFB) reactor system[J]. Chemical Engineering & Technology , 2009, 32 (3) :398–403. |
| [16] | Guío-Pérez D C, Hofbauer H, Pröll T. Effect of ring-type internals on solids distribution in a dual circulating fluidized bed system-cold flow model study[J]. AIChE Journal , 2013, 59 (10) :3612–3623. DOI:10.1002/aic.14120 |
| [17] | Schmid J C, Pröll T, Pfeifer C, et al, Improvement of gas-solid interaction in dual circulating fluidized bed systems[C]//Proc. 9th European Conference on Industrial Furnaces and Boilers (INFUB). Estoril, Portugal, 2011. |
 2016, Vol. 33
2016, Vol. 33 


